【數據結構】什麼是AVL樹
- 2019 年 10 月 3 日
- 筆記
什麼是AVL樹
二叉查找樹的一個局限性就是有可能退化成一個鏈表,這種情況下二叉查找樹的效率就會急劇下降變成0(n)。而AVL樹可以很好地解決BST的這種困境。本篇博客會介紹AVL樹的基本特點和相關操作。
文章參考自博客:二叉樹-你可能需要知道的知識點
1. 什麼是AVL樹
任何兩個子樹的高度差最大是1,這樣的二叉樹叫做AVL樹。
先來確定幾個概念:
平衡因子:將二叉樹上節點的左子樹高度減去右子樹高度的值稱為該節點的平衡因子BF(Balance Factor)。
最小不平衡子樹:距離插入節點最近的,且平衡因子的絕對值大於1的節點為根的子樹。
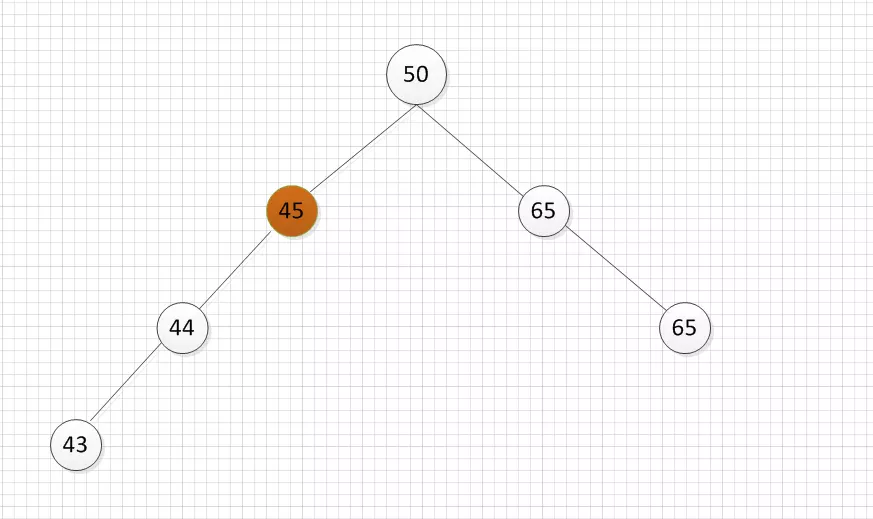
左邊二叉樹的節點45的BF = 1,插入節點43後,節點45的BF=2。
節點45是距離插入點43最近的BF不在[-1,1]範圍內的節點,因此以節點45為根的子樹為最小不平衡子樹。
2. 節點的實現
public class AVLTreeNode<T extends Comparable> { // 存儲的數據-用於排序 T key; // 節點高度-用於計算父節點的BF int height; // 左兒子 & 右兒子 AVLTreeNode<T> left; AVLTreeNode<T> right; public AVLTreeNode() { } public AVLTreeNode(T key, AVLTreeNode<T> left, AVLTreeNode<T> right) { this.key = key; this.left = left; this.right = right; this.height = 0; } } 節點的定義還是比較簡單的,相對於之前的定義多了一個height屬性用於計算父節點的BF。
樹的定義
public class AVLTree<T extends Comparable> { // 定義樹的根節點 AVLTreeNode<T> root; public AVLTree() { root = null; } } 獲取樹的高度
public int height() { return height(root); } private int height(AVLTreeNode<T> tree) { if (tree != null){ return tree.height; } return 0; } 本文章將空樹的高度定義為0,高度以樹的層次為準,根節點的高度為1,依次類推。
3. AVL樹的調整
如果在AVL樹中進行插入或刪除節點後,可能導致AVL樹失去平衡。這種不平衡可能出現在下面四種情況中:
- 對a的左兒子的左子樹進行一次插入。(LL)
- 對a的左兒子的右子樹進行一次插入。(LR)
- 對a的右兒子的左子樹進行一次插入。(RL)
- 對a的右兒子的右子樹進行一次插入。(RR)
其中1、4是關於a點的鏡像對稱,2、3是關於a點的鏡像對稱。
第一種情況(1、4)需要通過對樹的一次單旋轉完成調整。
第二種情況(2、3)需要通過對樹的一次雙旋轉完成調整。
3.1 LL旋轉
在左子樹上插入左孩子導致AVL樹失衡,"根的左子樹的高度"比"根的右子樹的高度"大2。針對該情況,我們需要進行單右旋轉來完成對樹的調整。
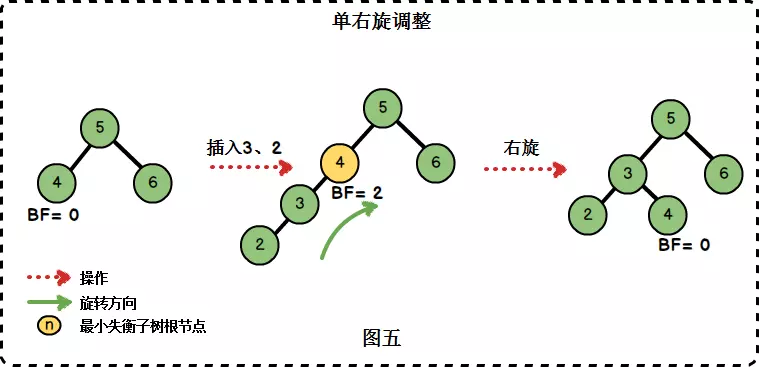
圖中左邊是旋轉之前的樹,右邊是旋轉之後的樹。從中可以發現,旋轉之後的樹又變成了AVL樹,而且該旋轉只需要一次即可完成。
對於LL旋轉,你可以這樣理解為:LL旋轉是圍繞"失去平衡的AVL根節點"進行的,也就是節點4;而且由於是LL情況,就將節點4進行一次順時針旋轉。
代碼實現:
/** * 進行一次單右旋轉 * * @param node 最小失衡樹根節點 */ private AVLTreeNode<T> rightRotation(AVLTreeNode<T> node) { AVLTreeNode<T> left = node.left; node.left = left.right; left.right = node; // 更新高度 node.height = Math.max(height(node.left), height(node.right)) + 1; left.height = Math.max(height(left.left), height(left.right)) + 1; return left; } 3.2 RR旋轉
在右子樹插入右孩子導致AVL失衡時,我們需要進行單左旋調整。旋轉圍繞最小失衡子樹的根節點進行。
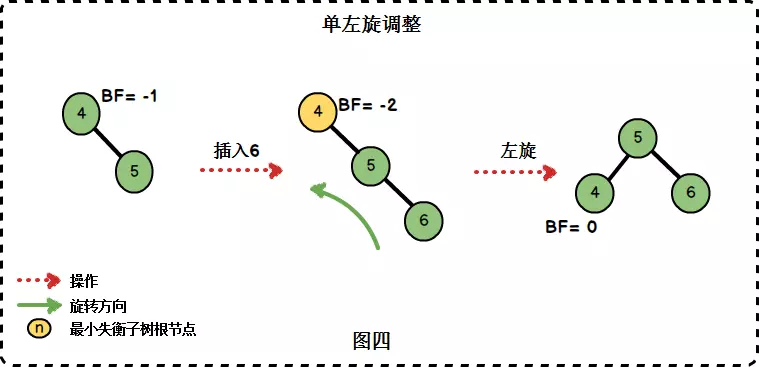
/** * 進行一次單左旋轉 * * @param node 最小失衡樹根節點 */ private AVLTreeNode<T> leftRotation(AVLTreeNode<T> node) { AVLTreeNode<T> right = node.right; node.right = right.left; right.left = node; // 更新高度 node.height = Math.max(height(node.left), height(node.right)) + 1; right.height = Math.max(height(right.left), height(right.right)) + 1; return right; } 3.3 RL旋轉
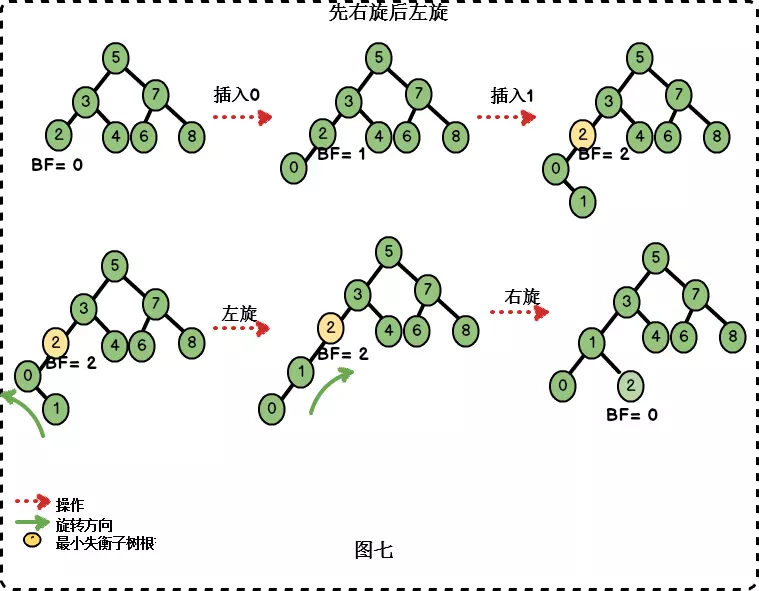
「在右子樹上插入左孩子導致AVL樹失衡",此時我們需要進行先右旋後左旋的調整。
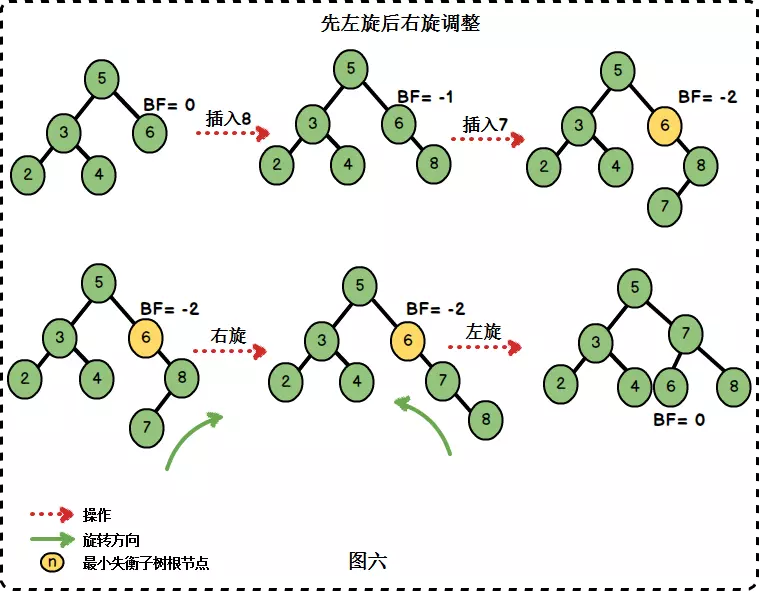
/** * 先右旋後左旋 * * @param node 失衡樹根節點 * @return 旋轉後的根節點 */ private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> node) { node.right = rightRoation(node.right); return leftRoation(node); } 3.4 LR旋轉
「在左子樹上插入右孩子導致AVL樹失衡",此時我們需要進行先左旋後右旋的調整。
/** * 先左旋後右旋 * * @param node 失衡樹根節點 * @return 旋轉後的根節點 */ private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> node) { node.left = leftRoation(node.left); return rightLeftRoation(node); } 