決勝經典算法之選擇排序
- 2019 年 10 月 3 日
- 筆記
習題答案
題目回顧
在上一篇文章中,我們以數列從小到大的排序方式為例,講了冒泡排序。並在結尾處拋出一個思考題:
如果要實現從大到小排列,上述代碼該做如何修改呢?
要解答這個問題十分簡單,如果讀者能明白從小到大排序的原理,就不難。
答案
根據冒泡排序法的原理,從小到大的排序是將較大元素依次排到最後。反之,從大到小的排序則是將較小的元素依次排到最後。
參考如下代碼:
public void bubbleSort(int[] arr) { for (int i = 1; i < arr.length; i++) { for (int j = 0; j < arr.length - i; j++) { if (arr[j] < arr[j + 1]) { int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; } } } }本篇的內容是第二種排序方法——選擇排序。
還是之前的問題:
問題挑戰
現有如下數字:
3,44,38,5,47,15,36,26,27,2,46,4,19,50,48
一共15個數字,請將其從小到大依次排列。
算法解析
所謂「選擇排序」,就是選出數列中最大或者最小(根據題目要求,本例則是選出最小的元素)的元素放在數列的靠前位置(稱為有序區)。然後再從剩餘的元素(稱為無序區)中選出最大或者最小的元素,放在已排序的部分後面。以此類推,直到結束。
怎麼樣?是不是感覺比冒泡排序更容易理解?還是先來看動圖演示吧:

詳細步驟
我們分步驟來拆解選擇排序的全過程:
- 初始狀態:無序區為R[1..n],有序區為空。
- 第i趟排序(i=1,2,3…n-1)開始時,當前有序區和無序區分別為R[1..i-1]和R(i..n)。該趟排序從當前無序區中-選出關鍵字最小的記錄 R[k],將它與無序區的第1個記錄R交換,使R[1..i]和R[i+1..n)分別變為記錄個數增加1個的新有序區和記錄個數減少1個的新無序區。
- n-1趟結束,數組有序化了。
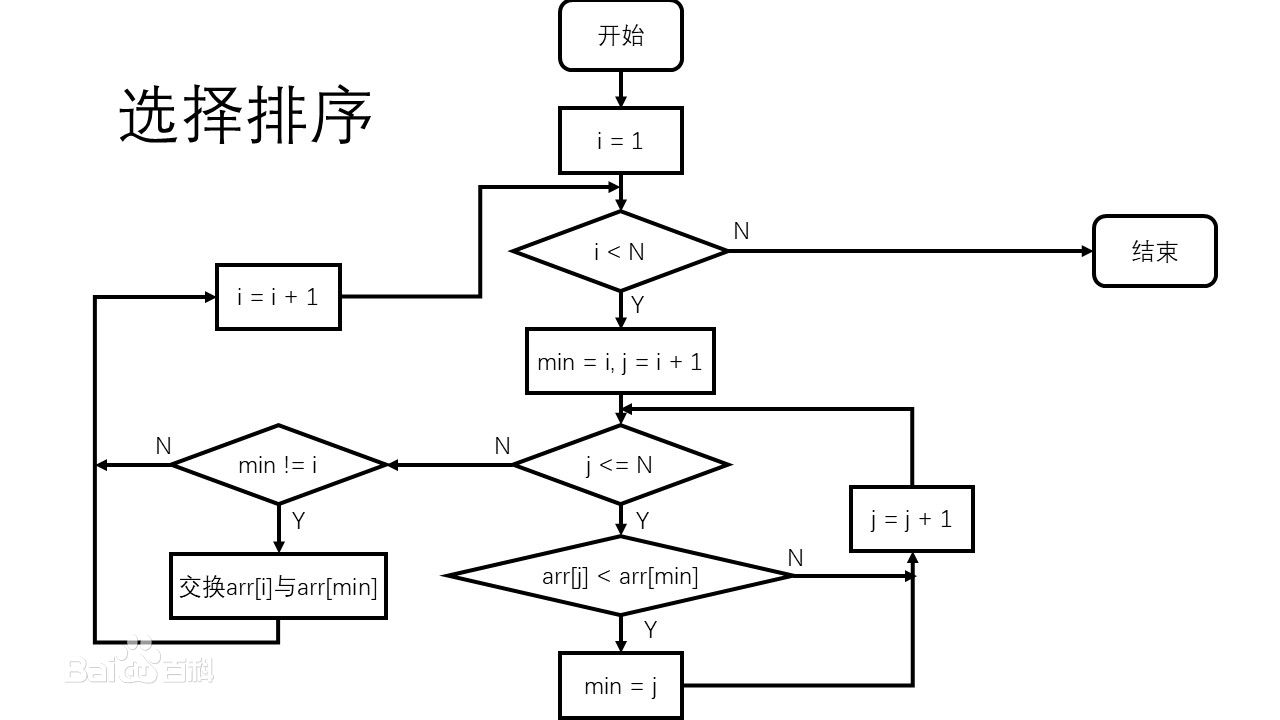
偽代碼
接下來,我們使用偽代碼實現上述過程。
SelectSort (input ele[],input length) for i <- 1 to length step 1 min <- i for j <- i+1 to length step 1 if ele[j] < ele[min] min <- j end if swap(ele[j],ele[min]) endJava代碼實現
具體到Java編程語言,實現上述算法的代碼如下所示:
public static void selectSort(int[] arr) { for (int i = 0; i < arr.length; i++) { int min = i; for (int j = i; j < arr.length; j++) { if (arr[j] < arr[min]) { min = j; } } if (min != i) { int temp = arr[i]; arr[i] = arr[min]; arr[min] = temp; } } }上述代碼中,參數arr表示未經排序的數列。該方法運行結束後,arr將變為從小到大排序的數列。
思考題
- 如果要實現從大到小排列,上述代碼該做如何修改呢?
思考題答案依舊會在下篇連載中公布,大家加油哦!
