典型的動態規劃題目總結(斐波那契數列相關)
- 2019 年 10 月 3 日
- 筆記
1.常規跳台階
一隻青蛙一次可以跳上1級台階,也可以跳上2級。求該青蛙跳上一個n級的台階總共有多少種跳法(先後次序不同算不同的結果)。
大體思路:
第 i 個樓梯可以從第 i-1 和 i-2 個樓梯再走一步到達,即走到第 i 個樓梯的方法數為走到第 i-1 和第 i-2 個樓梯的方法數之和。所以可以推導出遞推公式為:dp[i]=dp[i-1]+dp[i-2]
考慮到 dp[i] 只與 dp[i – 1] 和 dp[i – 2] 有關,因此可以只用兩個變量來存儲 dp[i – 1] 和 dp[i – 2],使得原來的 O(N) 空間複雜度優化為 O(1) 複雜度。具體非遞歸代碼如下:

2.變態跳台階
一隻青蛙一次可以跳上1級台階,也可以跳上2級……它也可以跳上n級。求該青蛙跳上一個n級的台階總共有多少種跳法。
大致思路:
(1)每一個高度的台階都可以一步完成,所以每一個位置都有一種基本解 dp[i]=1
(2)除了基本解之外,每一個高度的完成解還受到且僅受到前一個相鄰高度dp[i-1]的影響。
(3)因此,每一個高度的最終解都是前一個數的解()+本身的基本解。即,dp[i]=1+dp[i-1];

3.搶劫一排房子
你是一個專業的小偷,計劃偷竊沿街的房屋。每間房內都藏有一定的現金,影響你偷竊的唯一制約因素就是相鄰的房屋裝有相互連通的防盜系統,如果兩間相鄰的房屋在同一晚上被小偷闖入,系統會自動報警。給定一個代表每個房屋存放金額的非負整數數組,計算你在不觸動警報裝置的情況下,能夠偷竊到的最高金額。
大體思路:
(1)相鄰的房間不可以偷==》偷了i就不可以偷i-1.
(2)那麼假如i為一排房間的最後一間,那麼走過當前i個房間的最大值為:
dp[i]=max(dp[i-2]+numms[i],dp[i-1]);
因此,也需要兩個值dp[i-1],dp[i-2]。
class Solution { public int rob(int[] nums) { int pre1=0; int pre2=0; for(int i=0;i<nums.length;i++){ int temp=Math.max(nums[i]+pre2,pre1); pre2=pre1; pre1=temp; } return pre1; } }
4.搶劫一圈房子(環形的第一家和最後一家是相鄰的)
你是一個專業的小偷,計劃偷竊沿街的房屋,每間房內都藏有一定的現金。這個地方所有的房屋都圍成一圈,這意味着第一個房屋和最後一個房屋是緊挨着的。同時,相鄰的房屋裝有相互連通的防盜系統,如果兩間相鄰的房屋在同一晚上被小偷闖入,系統會自動報警。給定一個代表每個房屋存放金額的非負整數數組,計算你在不觸動警報裝置的情況下,能夠偷竊到的最高金額。
解題思路:
/**
(1)先考慮直線型的情況,當一共有i個房間時,偷了i,就不能再偷i-1.只能偷i-2.
所以 dp[i]=Math.max(nums[i]+dp[i-2],dp[i-1]);
(2)環形道的話,可以在直線型的基礎上進行考慮,因為第一和最後一個變成了相鄰,所以
偷了第一個就不能偷最後一個了。
從第二個開始偷,才可以偷最後一個。
因此,可以從這兩種路徑中選一個最大的作為最終的結果值。
**/
class Solution { public int rob(int[] nums) { //1.特殊值判斷 if(nums.length==1){ return nums[0]; } //環形解 int fromOne=maxVal(nums,0,nums.length-2); int fromTwo=maxVal(nums,1,nums.length-1); return Math.max(fromOne,fromTwo); } //直線型解 private int maxVal(int[]nums,int start,int end){ int pre1=0; int pre2=0; for(int i=start;i<=end;i++){ int temp=Math.max(nums[i]+pre2,pre1); pre2=pre1; pre1=temp; } return pre1; } }
5.大牛生小牛問題
假設農場中成熟的母牛每年都會生 1 頭小母牛,並且永遠不會死。第一年有 1 只小母牛,從第二年開始,母牛開始生小母牛。每隻小母牛 3 年之後成熟又可以生小母牛。給定整數 N,求 N 年後牛的數量。
思路:
(1)在前三年,只有母牛才可以生產。
(2)因為所有的牛都不會死,因此,第N-1年的所有牛dp[N-1]都會活到第N年。
(3) 因為成熟的母牛每年都會生 1 頭小母牛。因此,第N-3年中的所有牛到第N年都會新增一個小母牛。dp[N-3]。
N 年後牛的總數量為:一直的大母牛dp[N-1]+新增的小母牛dp[N-3]。

6.矩陣覆蓋問題
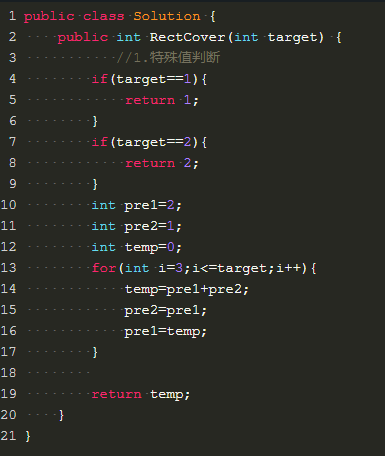
我們可以用2*1的小矩形橫着或者豎著去覆蓋更大的矩形。請問用n個2*1的小矩形無重疊地覆蓋一個2*n的大矩形,總共有多少種方法?
思路類似於常規跳台階。