機器學習(三):理解邏輯回歸及二分類、多分類代碼實踐
本文是機器學習系列的第三篇,算上前置機器學習系列是第八篇。本文的概念相對簡單,主要側重於代碼實踐。
上一篇文章說到,我們可以用線性回歸做預測,但顯然現實生活中不止有預測的問題還有分類的問題。我們可以從預測值的類型上簡單區分:連續變量的預測為回歸,離散變量的預測為分類。
一、邏輯回歸:二分類
1.1 理解邏輯回歸
我們把連續的預測值進行人工定義,邊界的一邊定義為1,另一邊定義為0。這樣我們就把回歸問題轉換成了分類問題。
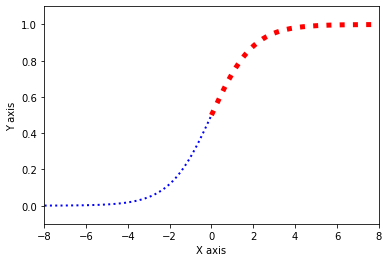
如上圖,我們把連續的變量分佈壓制在0-1的範圍內,並以0.5作為我們分類決策的邊界,大於0.5的概率則判別為1,小於0.5的概率則判別為0。
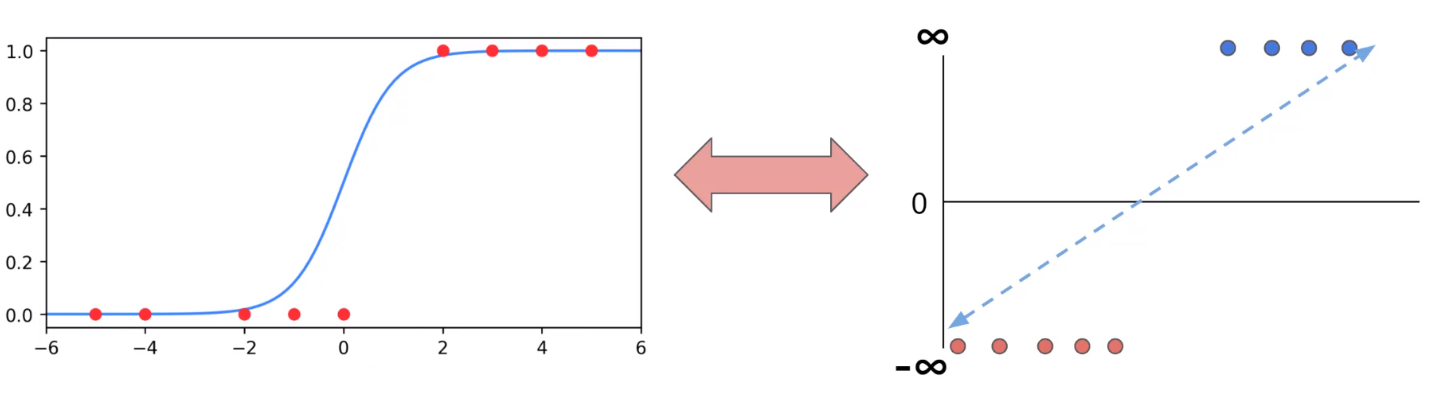
我們無法使用無窮大和負無窮大進行算術運算,我們通過邏輯回歸函數(Sigmoid函數/S型函數/Logistic函數)可以講數值計算限定在0-1之間。
$$ \sigma(x) = \frac{1}{1+e^{-x}} $$
以上就是邏輯回歸的簡單解釋。下面我們應用真實的數據案例來進行二分類代碼實踐。
1.2 代碼實踐 – 導入數據集
添加引用:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
導入數據集(大家不用在意這個域名):
df = pd.read_csv('//blog.caiyongji.com/assets/hearing_test.csv')
df.head()
| age | physical_score | test_result |
|---|---|---|
| 33 | 40.7 | 1 |
| 50 | 37.2 | 1 |
| 52 | 24.7 | 0 |
| 56 | 31 | 0 |
| 35 | 42.9 | 1 |
該數據集,對5000名參與者進行了一項實驗,以研究年齡和身體健康對聽力損失的影響,尤其是聽高音的能力。此數據顯示了研究結果對參與者進行了身體能力的評估和評分,然後必須進行音頻測試(通過/不通過),以評估他們聽到高頻的能力。
- 特徵:1. 年齡 2. 健康得分
- 標籤:(1通過/0不通過)
1.3 觀察數據
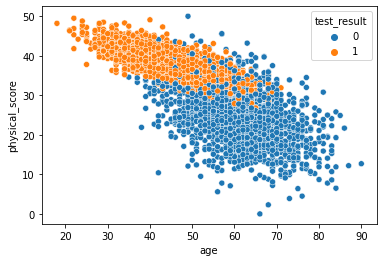
sns.scatterplot(x='age',y='physical_score',data=df,hue='test_result')
我們用seaborn繪製年齡和健康得分特徵對應測試結果的散點圖。
sns.pairplot(df,hue='test_result')
我們通過pairplot方法繪製特徵兩兩之間的對應關係。
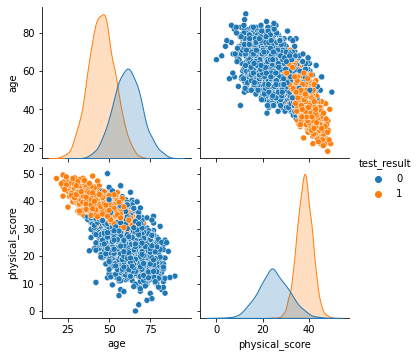
我們可以大致做出判斷,當年齡超過60很難通過測試,通過測試者普遍健康得分超過30。
1.4 訓練模型
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score,classification_report,plot_confusion_matrix
#準備數據
X = df.drop('test_result',axis=1)
y = df['test_result']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=50)
scaler = StandardScaler()
scaled_X_train = scaler.fit_transform(X_train)
scaled_X_test = scaler.transform(X_test)
#定義模型
log_model = LogisticRegression()
#訓練模型
log_model.fit(scaled_X_train,y_train)
#預測數據
y_pred = log_model.predict(scaled_X_test)
accuracy_score(y_test,y_pred)
我們經過準備數據,定義模型為LogisticRegression邏輯回歸模型,通過fit方法擬合訓練數據,最後通過predict方法進行預測。
最終我們調用accuracy_score方法得到模型的準確率為92.2%。
二、模型性能評估:準確率、精確度、召回率
我們是如何得到準確率是92.2%的呢?我們調用plot_confusion_matrix方法繪製混淆矩陣。
plot_confusion_matrix(log_model,scaled_X_test,y_test)
我們觀察500個測試實例,得到矩陣如下:
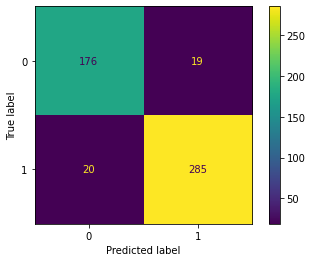
我們對以上矩陣進行定義如下:
- 真正類TP(True Positive) :預測為正,實際結果為正。如,上圖右下角285。
- 真負類TN(True Negative) :預測為負,實際結果為負。如,上圖左上角176。
- 假正類FP(False Positive) :預測為正,實際結果為負。如,上圖左下角19。
- 假負類FN(False Negative) :預測為負,實際結果為正。如,上圖右上角20。
準確率(Accuracy) 公式如下:
$$ Accuracy = \frac{TP+TN}{TP+TN+FP+FN} $$
帶入本例得:
$$ Accuracy = \frac{285+176}{285+176+20+19} = 0.922 $$
精確度(Precision) 公式如下:
$$ Precision = \frac{TP}{TP+FP} $$
帶入本例得:
$$ Precision = \frac{285}{285+19} = 0.9375 $$
召回率(Recall) 公式如下:
$$ Recall = \frac{TP}{TP+FN} $$
帶入本例得:
$$ Recall = \frac{285}{285+20} = 0.934 $$
我們調用classification_report方法可驗證結果。
print(classification_report(y_test,y_pred))

三、Softmax:多分類
3.1 理解softmax多元邏輯回歸
Logistic回歸和Softmax回歸都是基於線性回歸的分類模型,兩者無本質區別,都是從伯努利分結合最大對數似然估計。
最大似然估計:簡單來說,最大似然估計就是利用已知的樣本結果信息,反推最具有可能(最大概率)導致這些樣本結果出現的模型參數值。
術語「概率」(probability)和「似然」(likelihood)在英語中經常互換使用,但是它們在統計學中的含義卻大不相同。給定具有一些參數θ的統計模型,用「概率」一詞描述未來的結果x的合理性(知道參數值θ),而用「似然」一詞表示描述在知道結果x之後,一組特定的參數值θ的合理性。
Softmax回歸模型首先計算出每個類的分數,然後對這些分數應用softmax函數,估計每個類的概率。我們預測具有最高估計概率的類,簡單來說就是找得分最高的類。
3.2 代碼實踐 – 導入數據集
導入數據集(大家不用在意這個域名):
df = pd.read_csv('//blog.caiyongji.com/assets/iris.csv')
df.head()
| sepal_length | sepal_width | petal_length | petal_width | species |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 4.9 | 3 | 1.4 | 0.2 | setosa |
| 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5 | 3.6 | 1.4 | 0.2 | setosa |
該數據集,包含150個鳶尾花樣本數據,數據特徵包含花瓣的長度和寬度和萼片的長度和寬度,包含三個屬種的鳶尾花,分別是山鳶尾(setosa)、變色鳶尾(versicolor)和維吉尼亞鳶尾(virginica)。
- 特徵:1. 花萼長度 2. 花萼寬度 3. 花瓣長度 4 花萼寬度
- 標籤:種類:山鳶尾(setosa)、變色鳶尾(versicolor)和維吉尼亞鳶尾(virginica)
3.3 觀察數據
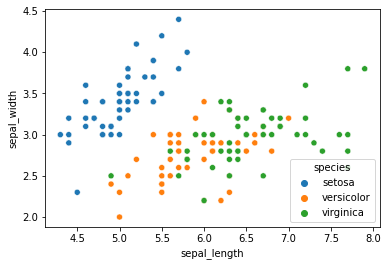
sns.scatterplot(x='sepal_length',y='sepal_width',data=df,hue='species')
我們用seaborn繪製花萼長度和寬度特徵對應鳶尾花種類的散點圖。
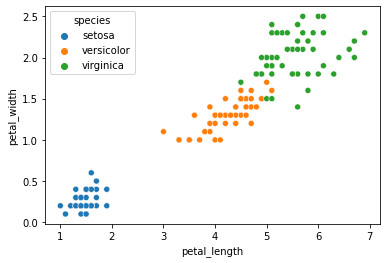
sns.scatterplot(x='petal_length',y='petal_width',data=df,hue='species')
我們用seaborn繪製花瓣長度和寬度特徵對應鳶尾花種類的散點圖。
sns.pairplot(df,hue='species')
我們通過pairplot方法繪製特徵兩兩之間的對應關係。

我們可以大致做出判斷,綜合考慮花瓣和花萼尺寸最小的為山鳶尾花,中等尺寸的為變色鳶尾花,尺寸最大的為維吉尼亞鳶尾花。
3.4 訓練模型
#準備數據
X = df.drop('species',axis=1)
y = df['species']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=50)
scaler = StandardScaler()
scaled_X_train = scaler.fit_transform(X_train)
scaled_X_test = scaler.transform(X_test)
#定義模型
softmax_model = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=50)
#訓練模型
softmax_model.fit(scaled_X_train,y_train)
#預測數據
y_pred = softmax_model.predict(scaled_X_test)
accuracy_score(y_test,y_pred)
我們經過準備數據,定義模型LogisticRegression的multi_class="multinomial"多元邏輯回歸模型,設置求解器為lbfgs,通過fit方法擬合訓練數據,最後通過predict方法進行預測。
最終我們調用accuracy_score方法得到模型的準確率為92.1%。
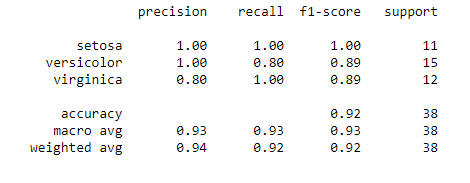
我們調用classification_report方法查看準確率、精確度、召回率。
print(classification_report(y_test,y_pred))
3.5 拓展:繪製花瓣分類
我們僅提取花瓣長度和花瓣寬度的特徵來繪製鳶尾花的分類圖像。
#提取特徵
X = df[['petal_length','petal_width']].to_numpy()
y = df["species"].factorize(['setosa', 'versicolor','virginica'])[0]
#定義模型
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=50)
#訓練模型
softmax_reg.fit(X, y)
#隨機測試數據
x0, x1 = np.meshgrid(
np.linspace(0, 8, 500).reshape(-1, 1),
np.linspace(0, 3.5, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
#預測
y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)
#繪製圖像
zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris virginica")
plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris versicolor")
plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris setosa")
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 7, 0, 3.5])
plt.show()
得到鳶尾花根據花瓣分類的圖像如下:
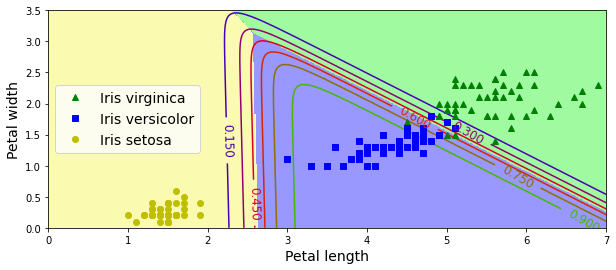
四、小結
相比於概念的理解,本文更側重上手實踐,通過動手編程你應該有「手熱」的感覺了。截至到本文,你應該對機器學習的概念有了一定的掌握,我們簡單梳理一下:
- 機器學習的分類
- 機器學習的工業化流程
- 特徵、標籤、實例、模型的概念
- 過擬合、欠擬合
- 損失函數、最小二乘法
- 梯度下降、學習率
7.線性回歸、邏輯回歸、多項式回歸、逐步回歸、嶺回歸、套索(Lasso)回歸、彈性網絡(ElasticNet)回歸是最常用的回歸技術 - Sigmoid函數、Softmax函數、最大似然估計
如果你還有不清楚的地方請參考:
- 機器學習(二):理解線性回歸與梯度下降並做簡單預測
- 機器學習(一):5分鐘理解機器學習並上手實踐
- 前置機器學習(五):30分鐘掌握常用Matplotlib用法
- 前置機器學習(四):一文掌握Pandas用法
- 前置機器學習(三):30分鐘掌握常用NumPy用法
- 前置機器學習(二):30分鐘掌握常用Jupyter Notebook用法
- 前置機器學習(一):數學符號及希臘字母

