Detecting rare visual relations using analogies 論文筆記

2021 年 2 月 1 日
AI
分類與分割

Background

論文動機：
- 各個實體的訓練樣本存在，但是它們的組合在訓練過程中很稀少或者是未出現過的。對所有可能的關係三元組收集足夠多的訓練數據是非常困難的
論文貢獻：
- 學習了結合subject、object以及predict individual embedding和表示關係三元組的visual phrase embedding的視覺關係表示方法。不同細粒度的表示，能夠捕獲更豐富的信息。
- 學習如何使用涉及相似object的關係之間的類比，將現有的訓練三元組visual phrase embedding遷移至未見過的關係三元組。
- 我們在兩個涉及rare and unseen具有挑戰性的數據集上展示我們的方法的優勢。

Model

第一部分

對subject (s)、object (o)、predicate (p)和visual phrase (vp)學習不同的visual-language embedding spaces。

假設訓練數據存在N個候選邊界框對。每一個候選邊界框對由subject candidate bounding box proposal 和 object candidate bounding box 組成。令\mathcal{V}_{s} 、 \mathcal{V}_{o} 、\mathcal{V}_{p} 分別表示 subject、object和 predicate 的詞彙表。則\mathcal{V}_{v p}=\mathcal{V}_{s} \times \mathcal{V}_{p} \times \mathcal{V}_{o} 表示三元組的詞彙表。

三元組t可以表示為t = (s , p , o)。對於每對subject 和 object邊界框，i \in [1 : N]，被標記為一個向量(y^{i}_{t})_{t \in {\mathcal{V}_{v p}}}。其中，當i^{th}對框能夠被關係三元組 t 描述時，y^{i}_{t} = 1，否則y^{i}_{t} = 0。subject、object和 predicate源於三元組標籤。（怎麼就源於三元組標籤了，怎麼通過三元組標籤去表示subject, object 和 predicate 的標籤？）

Learning representations of visual relations

在不同細粒度的 joint visual-semantic embedding spaces中，不同類型的embedding可以更好地表示視覺關係：

對於 unigram level，我們將 subject, object, predicate 表示在不同的 embedding space。
- visual embedding function的輸入為由其視覺表示 \mathbf{x}_{i} \in \mathbb{R}^{d_{v}}編碼的 object 候選對i。\mathbf{x}_{i}由CNN產生的視覺特徵和相關候選 object 相關的空間信息構成。
- language embedding 將一個由語言表示\mathbf{q}_{t} \in \mathbb{R}^{d_{q}}編碼三元組t作為輸入。\mathbf{x}_{i}由預訓練語言詞向量得到。
對於 trigram level，我們將整個三元組表示在 visual phrase embedding space。
網絡將subject, object 和 predicate的視覺特徵和語言特徵投影到獨立的空間。對於每一個輸入類型b \in \{s, o, p, vp \}，我們利用投影函數將視覺特徵和語言特徵嵌入到公共的d維空間中：

v^{b}_{i} = f^{b}_{v}(\mathbf{x}_{i}) (1)

w^{b}_{t} = f^{b}_{w}(\mathbf{q}_{t}) (2)

其中，v^{b}_{i}和w^{b}_{t}分別為視覺、語言表示輸出。投影函數為多層感知機。（是每一種輸入類型，有一個對應的投影函數，還是每一種細粒度對應一個投影函數？）
為了訓練embedding function的參數，最小化 log-likelihood：

\begin{aligned} \mathcal{L}_{b} &=\sum_{i=1}^{N} \sum_{t \in \mathcal{V}_{b}} \mathbb{1}_{y_{i}^{i}=1} \log \left(\frac{1}{1+e^{-\boldsymbol{w}_{t}^{b^{T}} \boldsymbol{v}_{i}^{b}}}\right) \\ &+\sum_{i=1}^{N} \sum_{t \in \mathcal{V}_{b}} \mathbb{1}_{y_{t}^{i}=0} \log \left(\frac{1}{1+e^{\boldsymbol{w}_{t}^{b^{T}} \boldsymbol{v}_{i}^{b}}}\right) \end{aligned}(3)

其中，第一個吸引項使visual representation v_{i}^{b}與其正確的language representation w^{b}_{t}更接近。第二個排斥項使不匹配的 visual-languale對分離。如上圖所示，對於每一種輸入類型都存在一個損失函數。訓練過程中，優化聯合損失：

\begin{aligned} \mathcal{L}_{joint} &=\mathcal{L}_{s} + \mathcal{L}_{o} + \mathcal{L}_{p} + \mathcal{L}_{vp}\end{aligned}(4)
推理期間，利用公式(1)將測試圖片嵌入為(v_{i}^{t})_{b}。類似地，利用公式(2)得到三元組t的編碼形式(w_{t}^{b})_{b}，作為language query。最後通過聚合不同嵌入類型的預測，計算triplet query t 與候選目標對 i 的相似性分數S：

S_{t, i}=\prod_{b \in\{s, p, o, v p\}} \frac{1}{1+e^{-\boldsymbol{w}_{t}^{b T} \boldsymbol{v}_{i}^{b}}} (5)

其中，b\in\{s, p, o, v p\}。
因為我們觀察到每種類型的嵌入會捕捉不同觀察到的視覺實體信息。如下圖所示，在 p 空間中，視覺實體person ride horse和person ride car因為相同的預測ride會被映射為同一點。比較而言，在 vp 空間中，這兩個實體會被映射為不同的點。這使得 vp 空間能夠很好地處理語言的多義詞（”ride”涉及的object不同時，會有不同的視覺表現，因此不能映射到同一點上）和同義詞（”person jump horse” 和 “person ride horse”應該被映射到靠近的點上，儘管它們預測的結果不同）。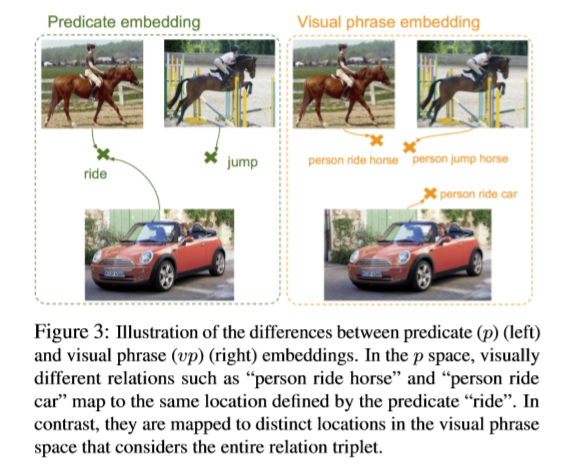

第二部分

Transferring embeddings to unseen triplets by analogy transformations

我們希望能夠顯式地通過類比推理，在測試期間，**將知識從訓練過程中出現的三元組知識遷移至未出現的三元組。**推理過程分為兩步：

如何從一個 visual phrase embedding 類比轉換到另一個。
- 為了將源三元組的t=(s, r, o)的 visual phrase embedding轉換成目標三元組t^{\prime}=\left(s^{\prime}, r^{\prime}, o^{\prime}\right)的 visual phrase embedding :
  
  \boldsymbol{w}_{t^{\prime}}^{v p}=\boldsymbol{w}_{t}^{v p}+\Gamma\left(t, t^{\prime}\right) (6)
  
  其中，\Gamma可以視為修正項，表示如何在聯合 visual-language空間中將\boldsymbol{w}_{t}^{v p}轉換為\boldsymbol{w}_{t^{\prime}}^{v p}，以計算與源三元組t類似的目標關係三元組t^{\prime}。
- 為了使 t 和 t^{\prime}的visual phrase embedding 通過\Gamma產生聯繫。將三元組分解為subject s, predicate p 和 object o。則公式(6)被改寫為：
  
  \boldsymbol{w}_{t^{\prime}}^{v p}=\boldsymbol{w}_{t}^{v p}+\Gamma\left[\begin{array}{c}\boldsymbol{w}_{t^{\prime}}^{s}-\boldsymbol{w}_{t}^{s} \\ \boldsymbol{w}_{t^{\prime}}^{p}-\boldsymbol{w}_{t}^{p} \\ \boldsymbol{w}_{t^{\prime}}^{o}-\boldsymbol{w}_{t}^{o}\end{array}\right] (7)
  
  其中，\boldsymbol{w}^{s}, \boldsymbol{w}^{p}和\boldsymbol{w}^{o}分別為對應的embedding。
  
  直覺上，我們希望\Gamma能夠對 object 的變化進行編碼。採用簡單的線性變換：
  
  \Gamma_{A}\left(t, t^{\prime}\right)=A\left[\begin{array}{c}w_{t^{\prime}}^{s}-w_{t}^{s} \\ w_{t^{\prime}}^{p}-w_{t}^{p} \\ w_{t^{\prime}}^{o}-w_{t}^{o}\end{array}\right] (8)
  
  其中，A \in \mathbb{R}^{d \times 3d}
- 通過最小化如下回歸損失學習 \Gamma 中的 A ：
  
  \mathcal{L}_{\text {transfer}}(A)=\sum_{i=1}^{N} \sum_{t^{\prime} \in \mathcal{V}_{v p}} \mathbb{1}_{y_{t}^{i}=1} \sum_{t \in \mathcal{N}_{t^{\prime}}}\left\|\boldsymbol{w}_{t^{\prime}}^{v p}-\tilde{\boldsymbol{w}}_{t}^{v p}(A)\right\|_{2} (9)
  
  其中，\tilde{\boldsymbol{w}}_{t}^{v p}(A) 為訓練目標三元組t^{\prime}的 viusal phrase embedding。\tilde{\boldsymbol{w}}_{t}^{v p}(A)=\boldsymbol{w}_{t}^{v p}+\Gamma_{A}\left(t, t^{\prime}\right) 為適合類比轉換的三元組轉換後的 visual phrase embedding。源三元組與目標三元組的 subject, object 和 predicate 只有一個不同。
確定哪一個 visual phrase 適合去進行推理。
- 測試期間，通過聚合相似的出現過的三元組t \in \mathcal{N}_{u}計算未出現過的三元組的 visual phrase embedding：
  
  \hat{\boldsymbol{w}}_{u}^{v p}=\sum_{t \in \mathcal{N}_{u}} G(t, u) \tilde{\boldsymbol{w}}_{t}^{v p} (10)
  
  其中，\tilde{\boldsymbol{w}}_{t}^{v p}=\boldsymbol{w}_{t}^{v p}+\Gamma\left(t, u\right)。具體可以分為兩步：
  - 通過 \Gamma 進行轉換。
  - 利用權重函數G進行聚合。G 根據每個三元組與u的相似性計算權重。對三元組進行分解，分別計算每種類型的相似性(因為 subject, object, predicate相較於 visual phrase space 而言限制較小)：
    
    G(t, u)=\sum_{b \in\{s, p, o\}} \alpha_{b} w_{t}^{b^{T}} w_{u}^{b} (11)
    
    利用點積計算相似性。\alpha_{b}為超參數。實際情況中，只保留k = 4個相似性最高的三元組通過公式(10)進行聚合。

Tags: 分類與分割