C. Three Bags【CF 1467】


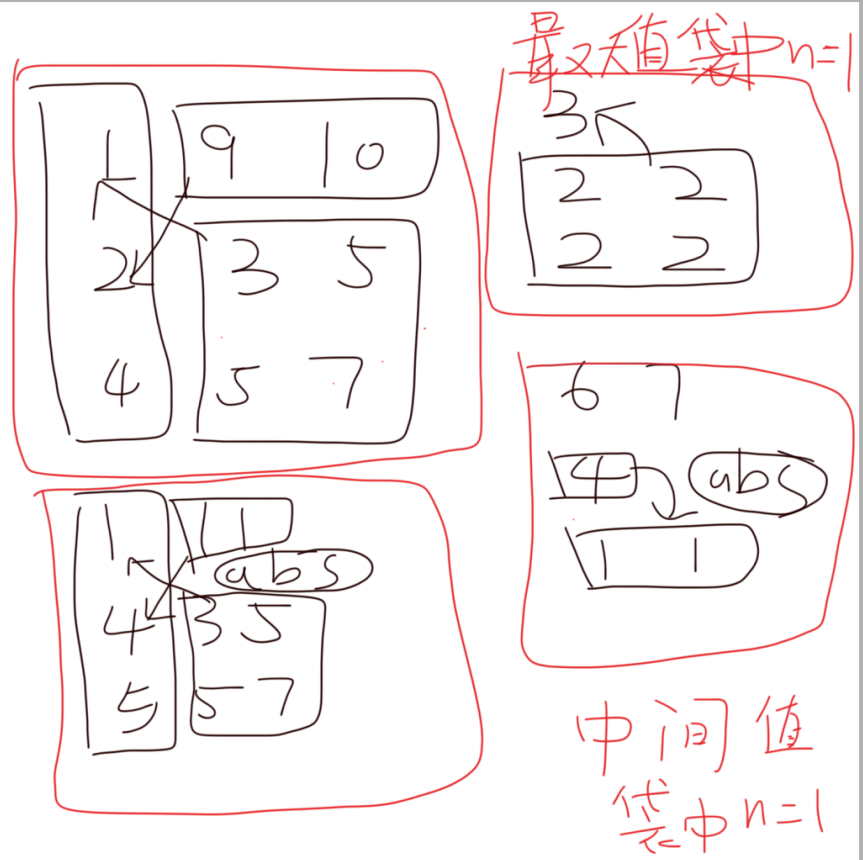
思路:對於一般情況,我們有三個袋子,容易想到把袋子里物品的價值排序。然後貪心,我們想讓最後的價值最大,則三個袋子最後都可以剩餘一個物品,這三個物品總和需要最大,最好的情況就是三個物品的符號「+」,「-」,「-」,這樣總價值直接可以算是每個袋子中物品絕對值的累加和。為了讓三個物品價值最大,我們可以容易想到,價值大的物品減去價值小的物品,讓可用價值儘可能大,而且最後剩餘每個袋子的最後物品符號分別是「+」「-」「-」。這樣,我們之前每個袋子的物品都排好了序,容易想到,對於三個袋子中,每個袋子價值最小的物品是關鍵。因為我們需要讓可用價值儘可能大,所以我們可以讓三個袋子中,最小值最大的那個物品為「+」,然後讓其他兩個袋子中的最小物品收集其他價值,這樣就滿足了三個袋子都只剩下一個物品且滿足「+」「-」「-」。我們可以讓最小值最大和最小值中間大的袋子中其他物品累加減去和最小值最小的物品讓其為「-」,然後讓最小值最小的其他物品累加和減去最小值中間大的那個物品讓其為「-」就可以了。但最小值最小的其他所有物品和最小值中間大的物品的差值會有特殊情況,例如:最小值的其他物品 1,1;中間值的最小值 4.這樣(4-1-1 = 2),這裡需要特判一下,我們發現兩者的差值只需要取一個abs就可以了,上面的例子可以轉化為:1 – 中間值放入最小值的袋中,變成了abs(-3+1)。
然後就是特殊情況,即三個袋子中任意一個袋子的物品只有一個的情況,需要特殊判斷。
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 #include <cmath> 6 #include <queue> 7 #include <vector> 8 #include <cstring> 9 #include <functional> 10 #include <map> 11 #define LL long long 12 #define lson(rt) (rt << 1) 13 #define rson(rt) (rt << 1 | 1) 14 using namespace std; 15 16 const int N = 1e3 + 10; 17 struct node 18 { 19 int v, id; 20 21 bool friend operator<(const node& a, const node& b) 22 { 23 return a.v < b.v; 24 } 25 }; 26 int a[N]; 27 28 void solve () 29 { 30 int n, m, k, x; 31 scanf("%d%d%d", &n, &m, &k); 32 vector<int > a[3]; 33 for(int i = 0; i < n; ++i) { 34 35 scanf("%d", &x); 36 a[0].push_back(x); 37 } 38 for(int i = 0; i < m; ++i) { 39 scanf("%d", &x); 40 a[1].push_back(x); 41 } 42 for(int i = 0; i < k; ++i) { 43 scanf("%d", &x); 44 a[2].push_back(x); 45 } 46 for(int i = 0; i < 3; ++i) sort(a[i].begin(), a[i].end()); 47 48 vector<node > vn; 49 vn.push_back({a[0][0], 0}); 50 vn.push_back({a[1][0], 1}); 51 vn.push_back({a[2][0], 2}); 52 53 sort(vn.begin(), vn.end()); 54 55 56 int maxx = vn[2].id; 57 int midd = vn[1].id; 58 int minn = vn[0].id; 59 60 long long maxv, midv, minv; 61 maxv = midv = minv = 0; 62 for(auto x : a[maxx]) maxv += x; 63 for(auto x : a[midd]) midv += x; 64 for(auto x : a[minn]) minv += x; 65 // printf("(%lld %lld %lld)\n", maxv, midv,minv); 66 midv -= a[midd][0]; 67 minv -= a[minn][0]; 68 maxv -= a[maxx][0]; 69 // printf("(%lld %lld %lld)\n", maxv, midv,minv); 70 // printf("(%d %d %d)\n", a[maxx].size(), a[midd].size(), a[minn].size()); 71 long long ans = 0; 72 if(a[minn].size() == 1) { 73 ans += maxv + midv + a[maxx][0] + a[midd][0] - a[minn][0]; 74 } else if(a[midd].size() == 1) { 75 // cout << "s" << endl; 76 ans += abs(minv + a[minn][0] - a[midd][0]); 77 ans += a[maxx][0] + maxv; 78 } else if(a[maxx].size() == 1 && a[maxx][0] < a[midd][0] + a[minn][0]) { 79 ans += midv + minv + a[midd][0] + a[minn][0] - a[maxx][0]; 80 } else { 81 // cout << "s" << endl; 82 ans += a[maxx][0] + maxv + midv - a[minn][0]; 83 ans += abs(minv - a[midd][0]); 84 } 85 86 printf("%lld\n", ans); 87 } 88 89 int main () 90 { 91 92 solve(); 93 94 return 0; 95 }


