[論文閱讀筆記] GEMSEC,Graph Embedding with Self Clustering
[論文閱讀筆記] GEMSEC: Graph Embedding with Self Clustering
本文結構
- 解決問題
- 主要貢獻
- 算法原理
- 參考文獻
(1) 解決問題
已經有一些工作在使用學習到的節點表示來做社區發現,但是僅僅局限在得到節點表示之後使用聚類算法來得到社區劃分,簡單說就是節點表示和目標任務分離了,學習到的節點表示並不能很有效地應用於聚類算法(因為可能節點表示向量所在的低維空間中並不存在容易容易劃分的簇,從而使用聚類算法也不能得到很好的社區劃分結果)。
(2) 主要貢獻
Contribution 1: 提出GEMSEC,一個基於序列的圖表徵模型,學習節點表徵的同時進行節點的聚類。
Contribution 2: 引入平滑正則項來迫使具有高度重疊鄰域的節點對有相似的節點表示。
(3) 算法原理
GEMSEC算法主要的框架還是遵循DeepWalk的算法框架,即隨機遊走生成語料庫,再利用簡單神經網絡來訓練節點表示向量。
- 對於隨機遊走部分,GEMSEC簡單採用DeepWalk的一階隨機遊走。
- 對於所使用的簡單神經網絡,原本DeepWalk採用的是以最大化窗口內節點共現概率為目標的Skip-Gram模型,而GEMSEC僅僅在Skip-Gram目標函數(窗口內節點的共現概率)的基礎上加上了和聚類有關的目標函數,從而將表示向量學習目標和聚類目標聯合在一起優化,得到更加適合聚類(簇的內聚程度高,簇間分明)的表示向量,在學習表示向量的同時也生成了節點的社區劃分。
總的目標函數=Skip-Gram目標函數+聚類目標函數,如下所示:
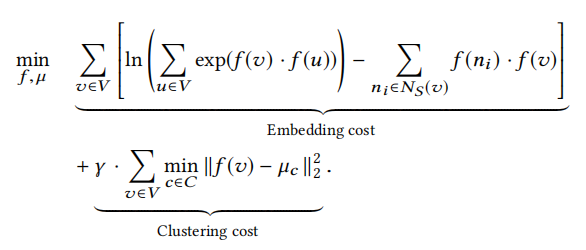
上述目標函數中用到的符號解釋如下:
\]
\]
\]
\]
\]
\]
上述目標函數中,第一項(公式中的Embedding cost)為使用了Softmax的節點共現概率函數化簡後的形式,主要作用是使得採樣的序列中同一個窗口內的節點的表示向量具有相似的表示。第二項(公式中的Clustering cost)為聚類的目標函數(類似Kmeans),旨在最小化節點與最近的聚類中心的距離,即增加簇的內聚度,訓練更適合聚類的表示向量。
此外論文中還引入了平滑正則化項(未在上述目標函數公式中給出),該項形式如下:
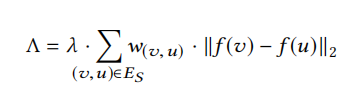
上述函數中用到的符號解釋如下:
\]
\]
\]
窗口內存在邊的節點對的正則化權重w(v,u)可由如下計算(採用網絡中的相似度計算方式確定,如Jaccard係數,即兩個節點共同鄰居的比例越大,兩個節點越相似):
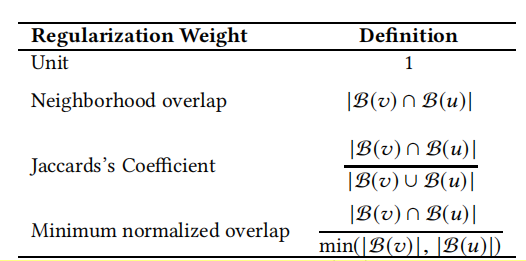
引入該平滑正則化項的目的是使得具有高度重疊鄰域的節點對有着更加相似的向量表示。 (該平滑正則化項也可以用於DeepWalk、Node2Vec等目標函數的設計)
因此最終Smooth GEMSEC算法的總的目標函數=共現概率目標+聚類目標+平滑正則化項。
(4) 參考文獻
Rozemberczki B, Davies R, Sarkar R, et al. Gemsec: Graph embedding with self clustering[C]//Proceedings of the 2019 IEEE/ACM international conference on advances in social networks analysis and mining. 2019: 65-72.

