程序員，你心裏需要有點樹

• 2019 年 10 月 3 日
• 筆記

看官，不要生氣，我沒有罵你也沒有鄙視你的意思，今天就是想單純的給大夥分享一下樹的相關知識，但是我還是想說作為一名程序員，自己心裏有沒有點樹？你會沒點數嗎？言歸正傳，樹是我們常用的數據結構之一，樹的種類很多有二叉樹、二叉查找樹、平衡二叉樹、紅黑樹、B樹、B+樹等等，我們今天就來聊聊二叉樹相關的樹。

什麼是樹?

首先我們要知道什麼是樹？我們平常中的樹是往上長有分支的而卻不會形成閉環，數據結構中的樹跟我們我們平時看到的樹類似，確切的說是跟樹根長得類似，我畫了一幅圖，讓大家更好的理解樹。

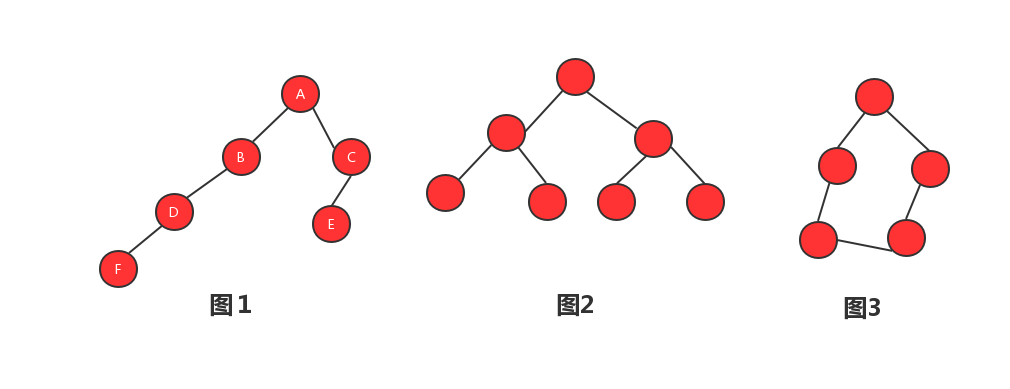
圖１、圖２都是樹，圖３不是樹。每個紅色的圓圈我們稱之為元素也叫節點，用線將兩個節點連接起來，這兩個節點就形成了父子關係,同一個父節點的子節點成為兄弟節點，這跟我們家族關係一樣，同一個父親的叫做兄弟姐妹，在家族裏面最大的稱為老子，樹裏面也是一樣的，只是不叫老子，叫做跟節點，沒有子節點的叫做葉子節點。我們拿圖１來做示例，A為根節點，B、C為兄弟節點，E、F為葉子節點。

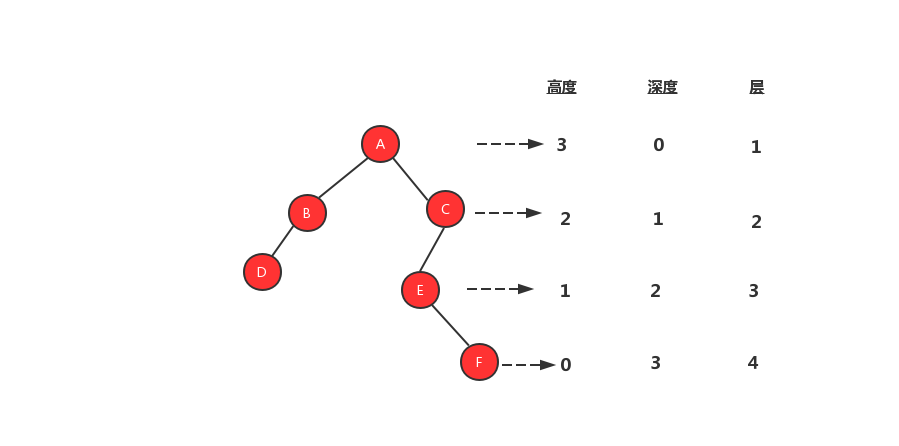
一顆樹還會涉及到三個概念高度、深度、層，我們先來看看這三個名詞的定義：

高度：節點到葉子節點的最長路徑，從０開始計數

深度：跟節點到這個節點所經歷的邊數，從０開始計數

層：節點距離根節點的距離，從１開始計數

知道了三個名詞的概念之後，我們用一張圖來更加形象的表示這三個概念。

以上就是樹的基本概念，樹的種類很多，我們主要來學學二叉樹。

二叉樹

二叉樹就像它的名字一樣，每個元素最多有兩個節點，分別稱為左節點和右節點。當然並不是每個元素都需要有兩個節點，有的可能只有左節點，有的可能只有右節點。就像國家開放二胎一樣，也不是每個人都需要生兩個孩子。下面我們來看看一顆典型的二叉樹。

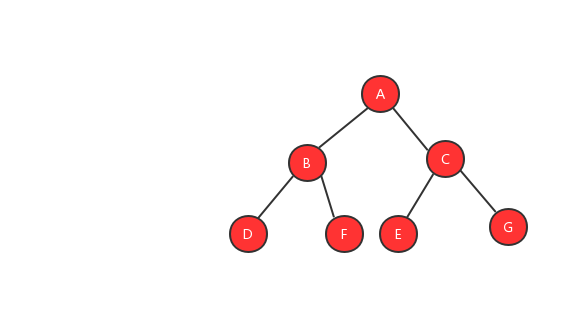
基於樹的存儲模式的不同，為了更好的利用存儲空間，二叉樹又分為完全二叉樹和非完全二叉樹，我們先來看看什麼是完全二叉樹、非完全二叉樹？

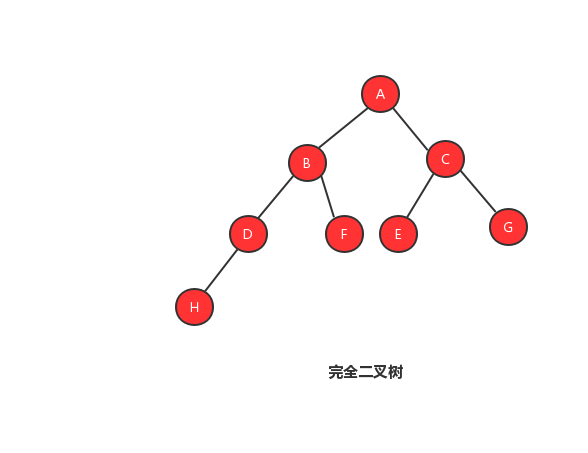
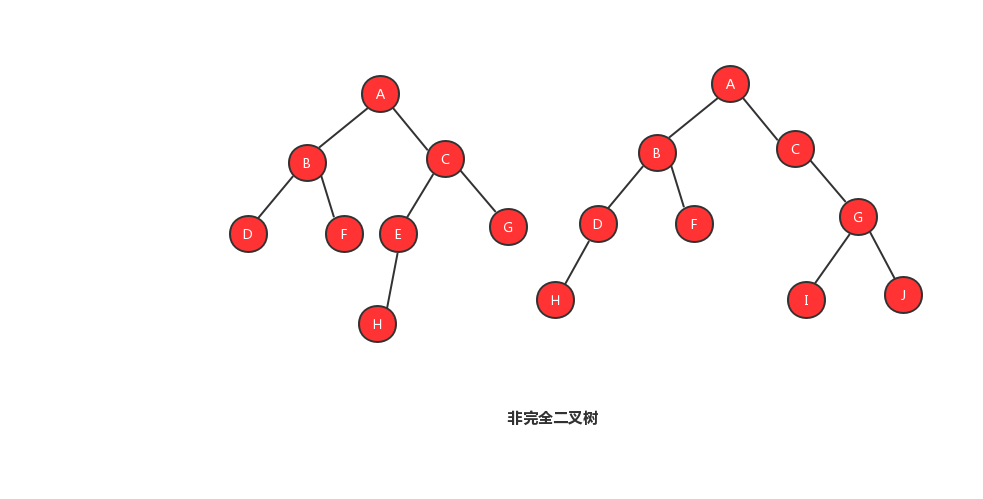
完全二叉樹的定義：葉子節點都在最底下兩層，最後一層的葉子節點都靠左排列，並且除了最後一層，其他層的節點個數都要達到最大

也許單看定義會看不明白，我們來看幾張圖，你就能夠明白什麼是完全二叉樹、非完全二叉樹。

１、完全二叉樹

２、非完全二叉樹

上面我們說了基於樹的存儲模式不同，而分為完全二叉樹和非完全二叉樹，那我們接下來來看看樹的存儲模式。

二叉樹的存儲模式

二叉樹的存儲模式有兩種，一種是基於指針或者引用的二叉鏈式存儲法，一種是基於數組的順序存儲法

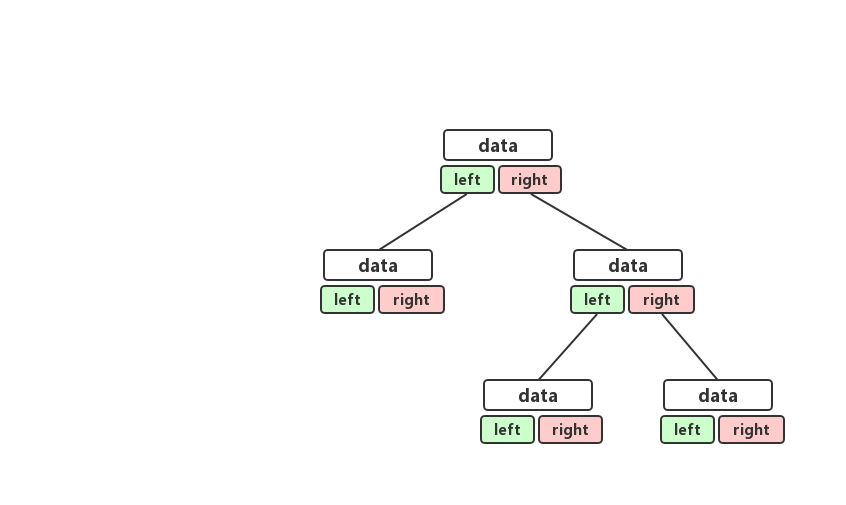
二叉鏈式存儲法

鏈式存儲法相對比較簡單，理解起來也非常容易，每一個節點都有三個字段，一個字段存儲着該節點的值，另外兩個字段存儲着左右節點的引用。我們順着跟位元組就可以很輕鬆的把整棵樹串起來，鏈式存儲法的結構大概長成這樣。

順序存儲法

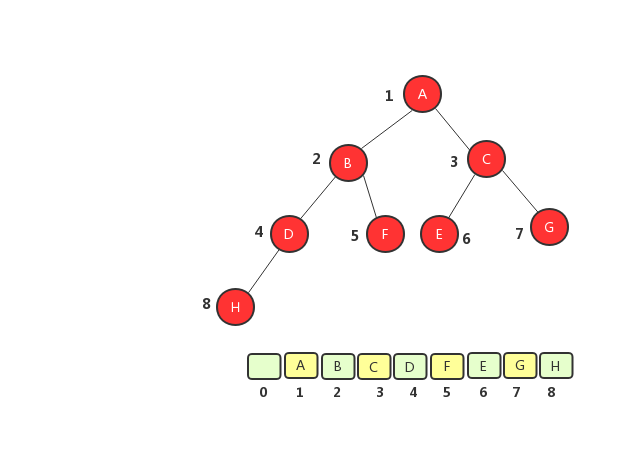
順序存儲法是基於數組實現的，數組是一段有序的內存空間，如果我們把跟節點的坐標定位i=1，左節點就是 2 * i = 2，右節點 2 * i+ 1 = 3，以此類推，每個節點都這麼算，然後就將樹轉化成數組了，反過來，按照這種規則我們也能將數組轉化成一棵樹。看到這裡我想你一定看出了一些弊端， 如果這是一顆不平衡的二叉樹是不是會造成大量的空間浪費呢？沒錯，這就是為什麼需要分完全二叉樹和非完全二叉樹。分別來看看這兩種樹基於數組的存儲模式。

完全二叉樹順序存儲法

非完全二叉樹順序存儲法

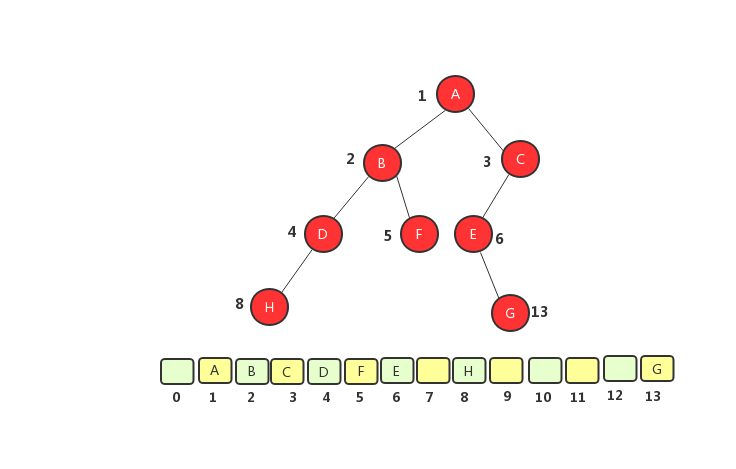
從圖中將樹轉化成數組之後可以看出，完全二叉樹用數組來存儲只浪費了一個下標為0的存儲空間，二非完全二叉樹則浪費了大量的空間。如果樹為完全二叉樹，用數組存儲比鏈式存儲節約空間，因為數組存儲不需要存儲左右節點的信息

上面我們了解了二叉樹的定義、類型、存儲方式，接下來我們一起了解一下二叉樹的遍歷，二叉樹的遍歷也是面試中經常遇到的問題。

二叉樹遍歷

要了解二叉樹的遍歷，我們首先需要實例化出一顆二叉樹，我們採用鏈式存儲的方式來定義樹，實例化樹需要樹的節點信息，用來存放該節點的信息，因為我們才用的是鏈式存儲，所以我們的節點信息如下。

/**   * 定義一棵樹   */  public class TreeNode {      // 存儲值      public int data;      // 存儲左節點      public TreeNode left;      // 存儲右節點      public TreeNode right;        public TreeNode(int data) {          this.data = data;      }  }  

定義完節點信息之後，我們就可以初始化一顆樹啦，下面是初始化樹的過程:

public static TreeNode buildTree() {      // 創建測試用的二叉樹      TreeNode t1 = new TreeNode(1);      TreeNode t2 = new TreeNode(2);      TreeNode t3 = new TreeNode(3);      TreeNode t4 = new TreeNode(4);      TreeNode t5 = new TreeNode(5);      TreeNode t6 = new TreeNode(6);      TreeNode t7 = new TreeNode(7);      TreeNode t8 = new TreeNode(8);        t1.left = t2;      t1.right = t3;      t2.left = t4;      t4.right = t7;      t3.left = t5;      t3.right = t6;      t6.left = t8;        return t1;  }

經過上面步驟之後，我們的樹就長成下圖所示的樣子，數字代表該節點的值。

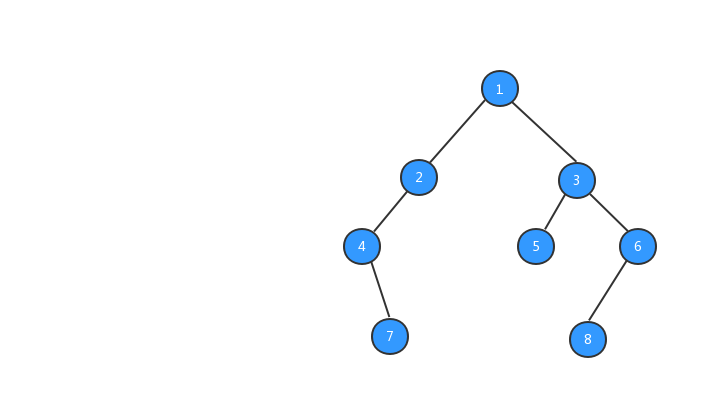
有了樹之後，我們就可以對樹進行遍歷啦，二叉樹的遍歷有三種方式，前序遍歷、中序遍歷、後續遍歷三種遍歷方式，三種遍歷方式與節點輸出的順序有關係。下面我們分別來看看這三種遍歷方式。

前序遍歷

前序遍歷：對於樹中的任意節點來說，先打印這個節點，然後再打印它的左子樹，最後打印它的右子樹。

為了方便大家的理解，我基於上面我們定義的二叉樹，對三種遍歷方式的執行流程都製作了動態圖，希望對你的閱讀有所幫助，我們先來看看前序遍歷的執行流程動態圖。

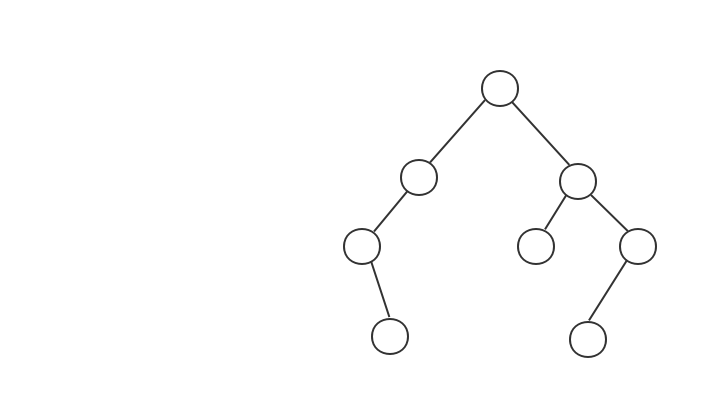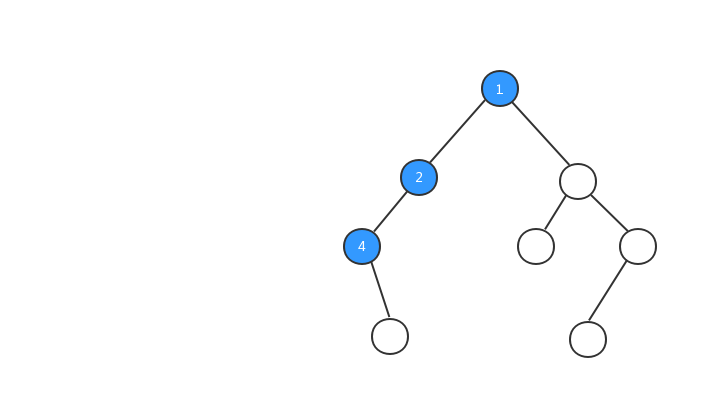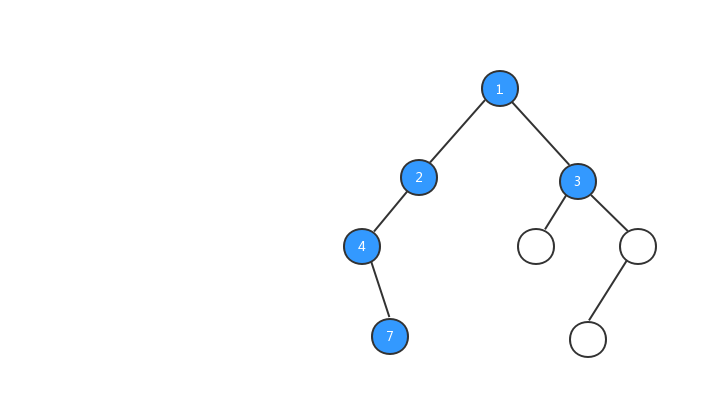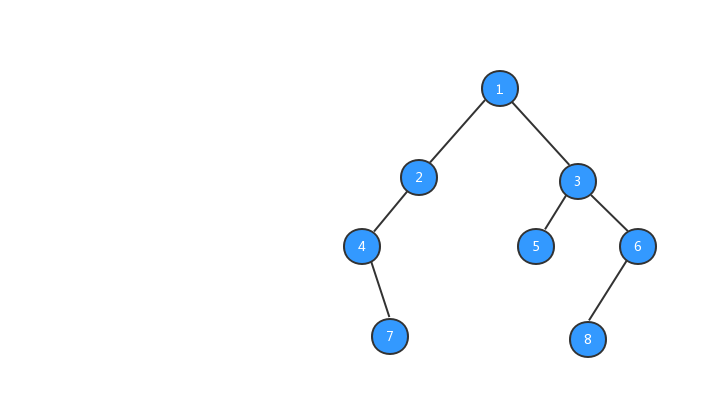
理解了前序遍歷的概念和看完前序遍歷執行流程動態圖之後，你心裏一定很想知道，在代碼中如何怎麼實現樹的前序遍歷？二叉樹的遍歷非常簡單，一般都是採用遞歸的方式進行遍歷，我們來看看前序遍歷的代碼：

// 先序遍歷，遞歸實現 先打印本身，再打印左節點，在打印右節點  public static void preOrder(TreeNode root) {        if (root == null) {          return;      }      // 輸出本身      System.out.print(root.data + " ");      // 遍歷左節點      preOrder(root.left);      // 遍歷右節點      preOrder(root.right);  }

中序遍歷

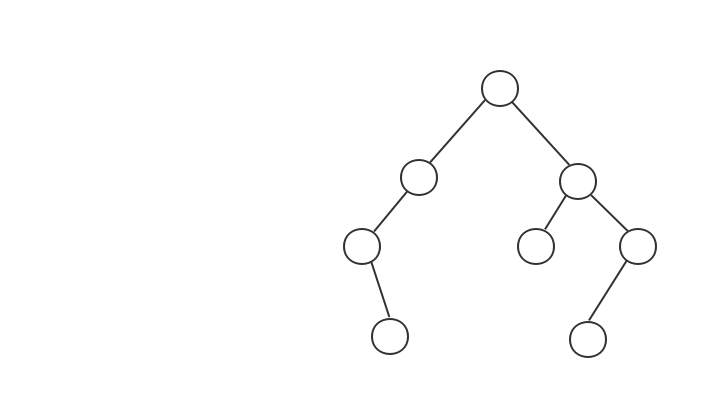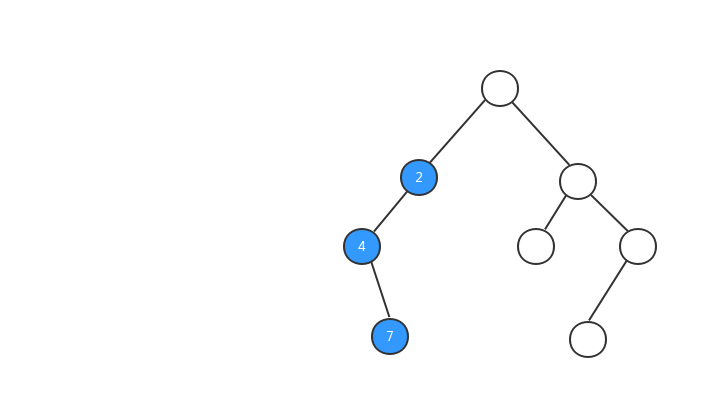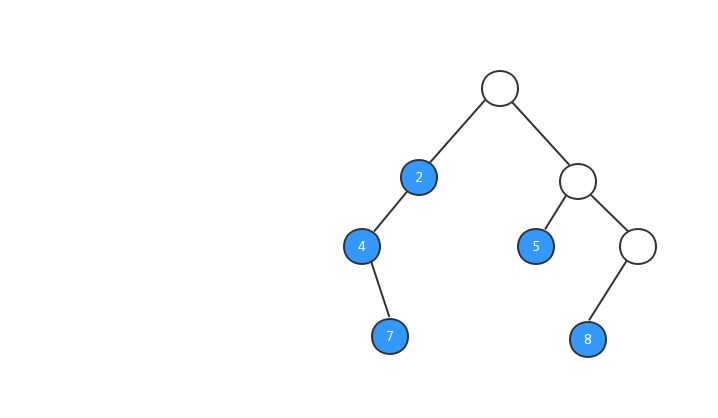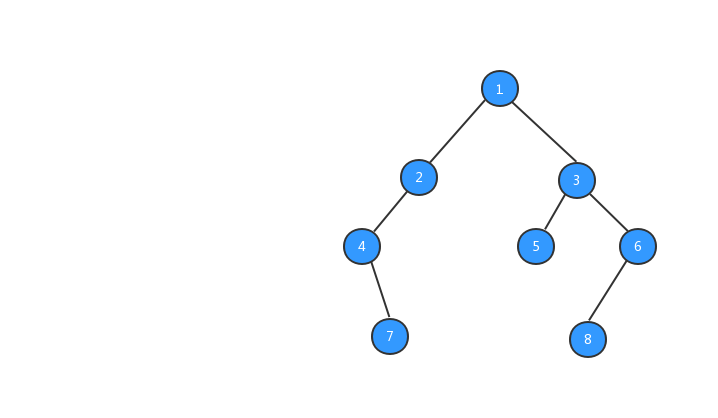
中序遍歷：對於樹中的任意節點來說，先打印它的左子樹，然後再打印它本身，最後打印它的右子樹。

跟前序遍歷一樣，我們來看看中序遍歷的執行流程動態圖。

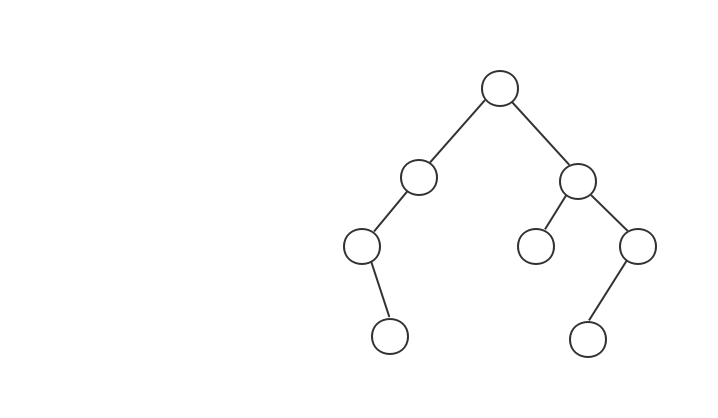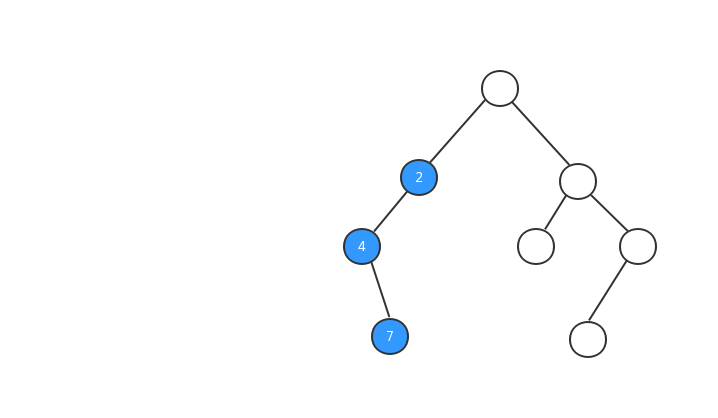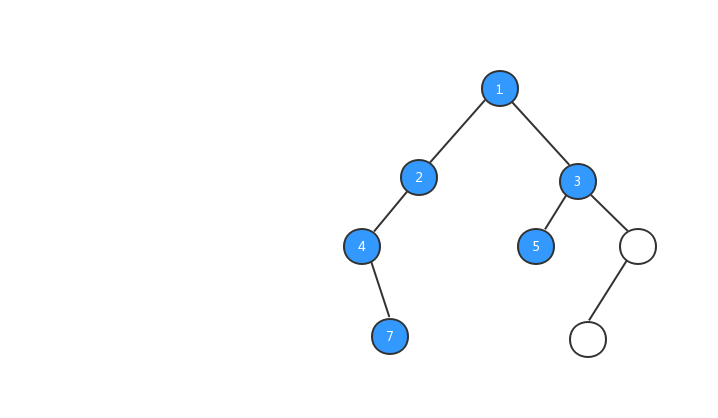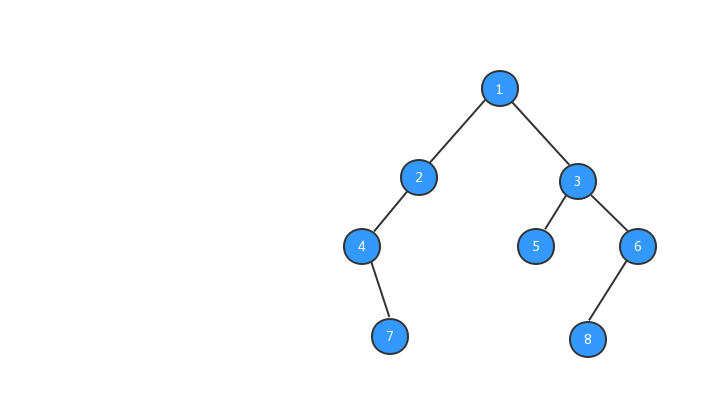
中序遍歷的代碼：

// 中序遍歷 先打印左節點，再輸出本身，最後輸出右節點  public static void inOrder(TreeNode root) {      if (root == null) {          return;      }      inOrder(root.left);      System.out.print(root.data + " ");      inOrder(root.right);  }

後序遍歷

後序遍歷：對於樹中的任意節點來說，先打印它的左子樹，然後再打印它的右子樹，最後打印這個節點本身。

跟前兩種遍歷一樣，理解概念之後，我們還是先來看張圖。

後序遍歷的實現代碼：

// 後序遍歷 先打印左節點，再輸出右節點，最後才輸出本身  public static void postOrder(TreeNode root) {      if (root == null) {          return;      }      postOrder(root.left);      postOrder(root.right);      System.out.print(root.data + " ");  }

二叉樹的遍歷還是非常簡單的，雖然有三種遍歷方式，但都是一樣的，只是輸出的順序不一樣而已，經過了上面這麼多的學習，我相信你一定對二叉樹有不少的認識，接下來我們來了解一種常用而且比較特殊的二叉樹：二叉查找樹

二叉查找樹

二叉查找樹又叫二叉搜索樹，從名字中我們就能夠知道，這種樹在查找方面一定有過人的優勢，事實確實如此，二叉查找樹確實是為查找而生的樹，但是它不僅僅支持快速查找數據，還支持快速插入、刪除一個數據。那它是怎麼做到這些的呢？我們先從二叉查找樹的概念開始了解。

二叉查找樹：在樹中的任意一個節點，其左子樹中的每個節點的值，都要小於這個節點的值，而右子樹節點的值都大於這個節點的值。

難以理解？記不住？沒關係的，下面我定義了一顆二叉查找樹，我們對着樹，來慢慢理解。

根據二叉查找樹的定義，每棵樹的左節點的值要小於這父節點，右節點的值要大於父節點。62節點的 所有左節點的值都要小於 62 ，所有右節點 的值都要大於 62 。對於這顆樹上的每一個節點都要滿足這個條件，我們拿我們樹上的另一個節點 35 來說，它的右子樹上的節點值最大不能超過 47 ，因為 35 是 47 的左子樹，根據二叉搜索樹的規則，左子樹的值要小於節點值。

二叉查找樹既然名字中帶有查找兩字，那我們就從二叉查找樹的查找開始學習二叉查找樹吧。

二叉查找樹的查找操作

由於二叉查找樹的特性，我們需要查找一個數據，先跟跟節點比較，如果值等於跟節點，則返回根節點，如果小於根節點，則必然在左子樹這邊，只要遞歸查找左子樹就行，如果大於，這在右子樹這邊，遞歸右子樹即可。這樣就能夠實現快速查找，因為每次查找都減少了一半的數據，跟二分查找有點相似，快速插入、刪除都是居於這個特性實現的。

下面我們用一幅動態圖來加強對二叉查找樹查找流程的理解，我們需要在上面的這顆二叉查找樹中找出值等於 37 的節點，我們一起來看看流程圖是怎麼實現的。

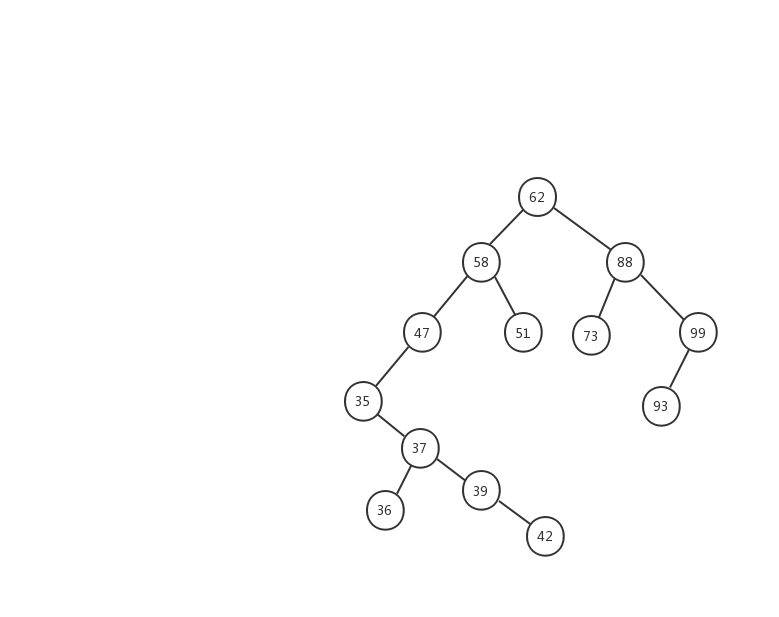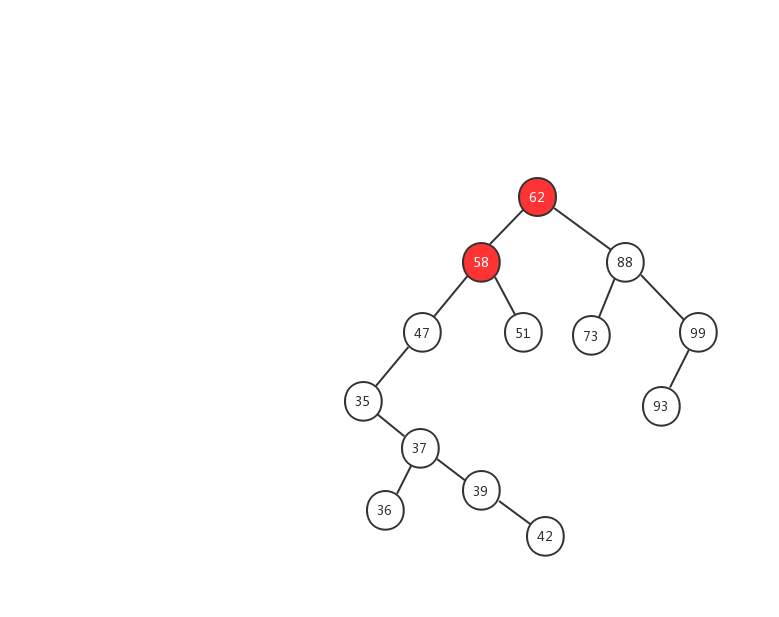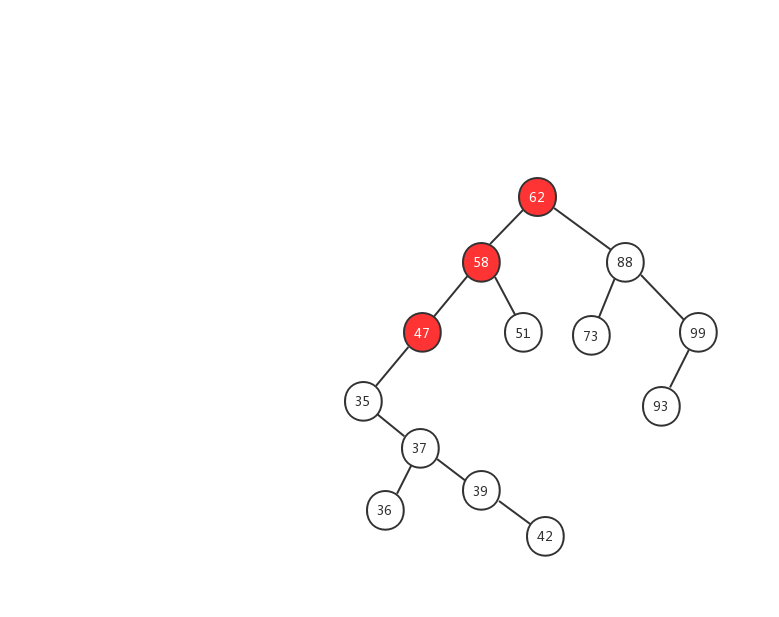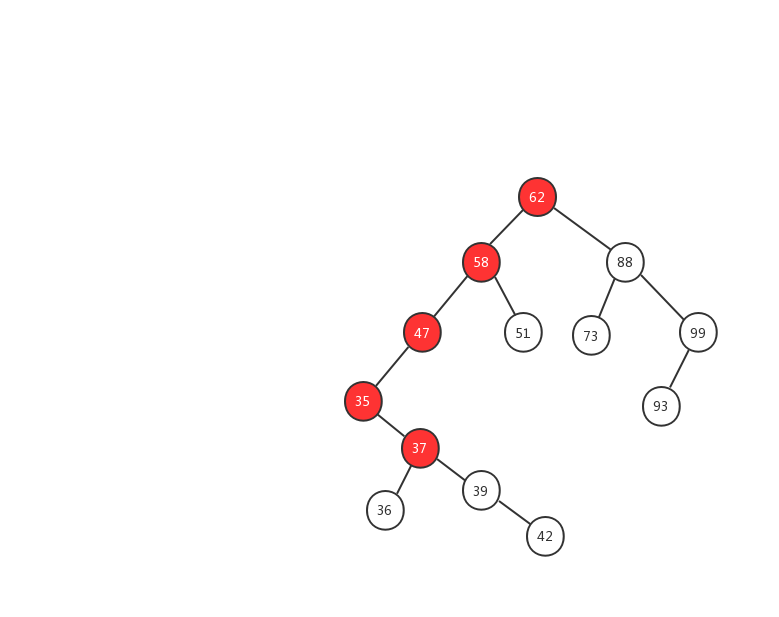
• 1、先用 37 跟 62 比較，37 < 62 ，在左子樹中繼續查找
• ２、左子樹的節點值為 58，37 < 58 ，繼續在左子樹中查找
• ３、左子樹的節點值為 47，37 < 47，繼續在左子樹中查找
• ４、左子樹的節點值為 35，37 > 35，在右子樹中查找
• ５、右子樹中的節點值為 37，37 = 37 ，返回該節點

講完了查找的概念之後，我們一起來看看二叉查找樹的查找操作的代碼實現

/**   * 根據值查找樹   * @param data　值   * @return   */  public TreeNode find(int data) {      TreeNode p = tree;      while (p != null) {          if (data < p.data) p = p.left;          else if (data > p.data) p = p.right;          else return p;      }      return null;  }

二叉查找樹的插入操作

插入跟查找差不多，也是從根節點開始找，如果要插入的數據比節點的數據大，並且節點的右子樹為空，就將新數據直接插到右子節點的位置；如果不為空，就再遞歸遍歷右子樹，查找插入位置。同理，如果要插入的數據比節點數值小，並且節點的左子樹為空，就將新數據插入到左子節點的位置；如果不為空，就再遞歸遍歷左子樹，查找插入位置。

假設我們要插入 63 ，我們用一張動態圖來看看插入的流程。

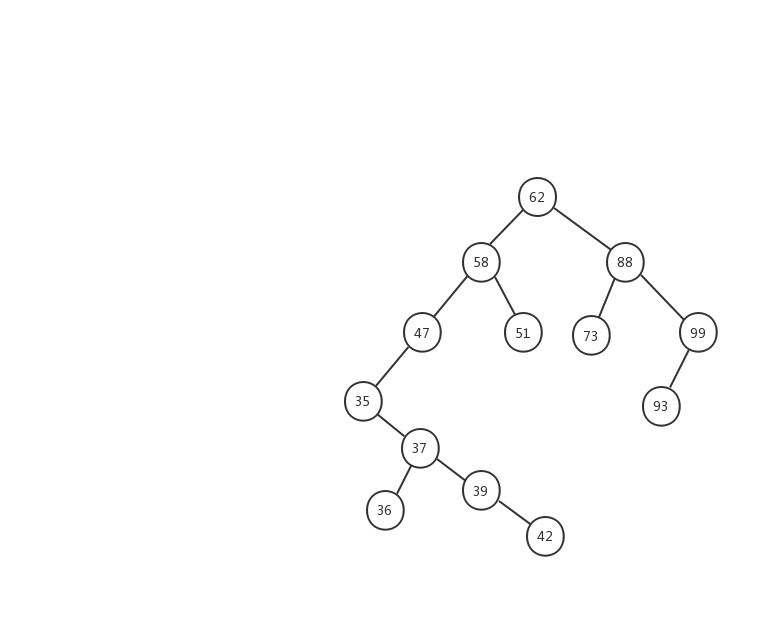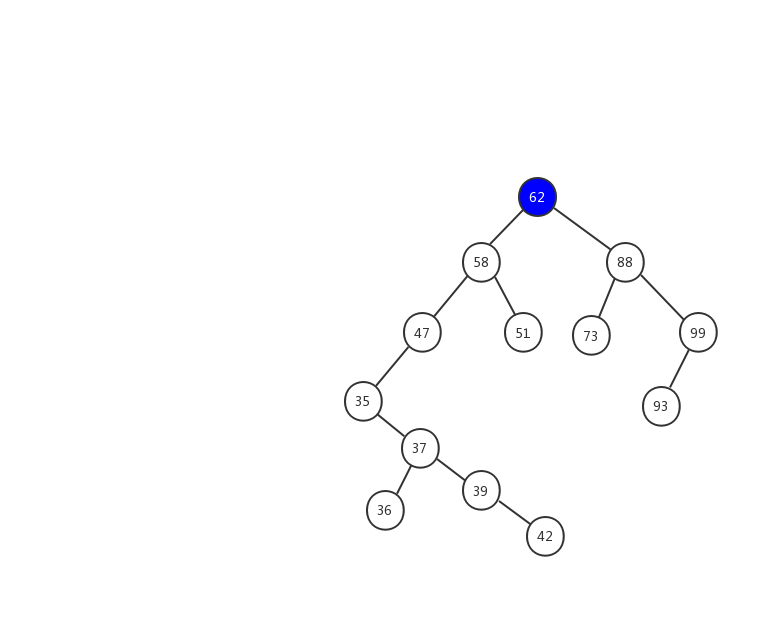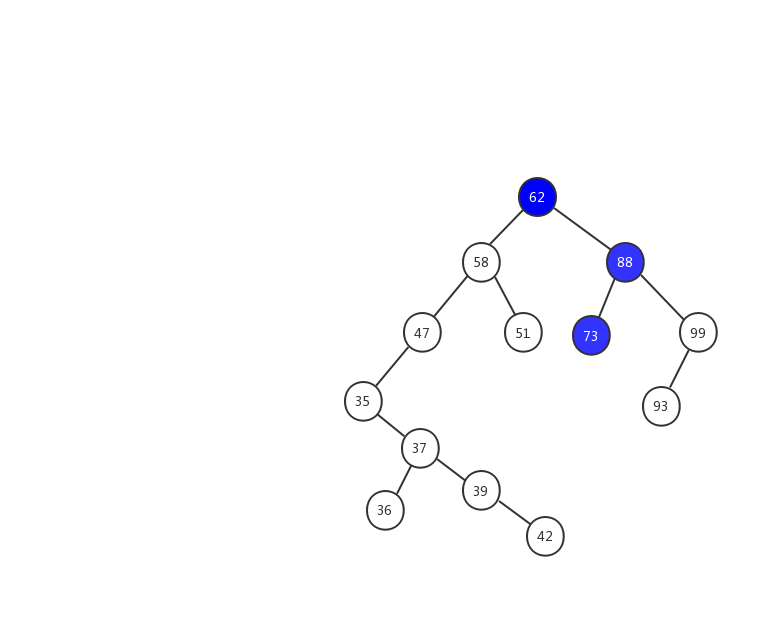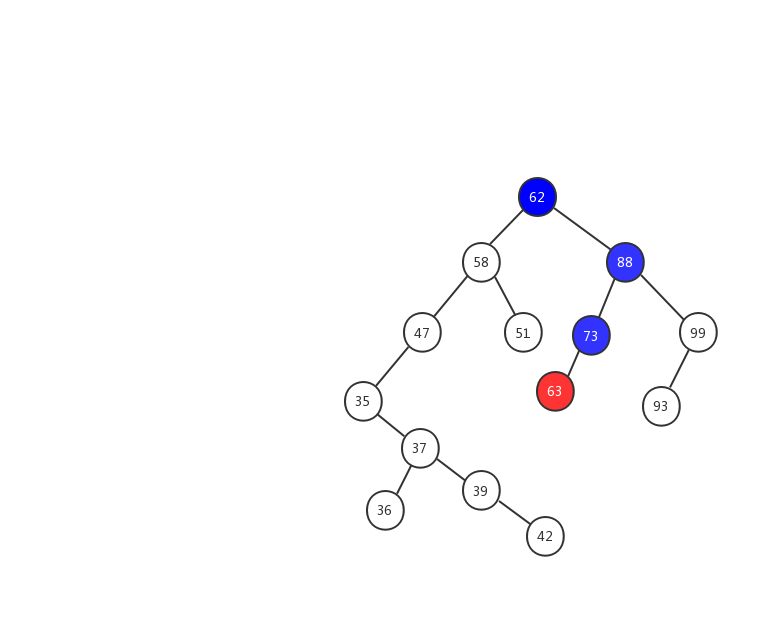
• 1、63 > 62 ，在樹的右子樹繼續查找.
• 2、63 < 88 ，在樹的左子樹繼續查找
• 3、63 < 73 ,因為 73 是葉子節點，所以 63 就成為了 73 的左子樹。

我們來看看二叉查找樹的插入操作實現代碼

/**   * 插入樹   * @param data   */  public void insert(int data) {      if (tree == null) {          tree = new TreeNode(data);          return;      }        TreeNode p = tree;        while (p != null) {          // 如果值大於節點的值，則新樹為節點的右子樹          if (data > p.data) {              if (p.right == null) {                  p.right = new TreeNode(data);                  return;              }              p = p.right;          } else { // data < p.data              if (p.left == null) {                  p.left = new TreeNode(data);                  return;              }              p = p.left;          }      }  }

二叉查找樹的刪除操作

刪除的邏輯要比查找和插入複雜一些，刪除分一下三種情況：

第一種情況：如果要刪除的節點沒有子節點，我們只需要直接將父節點中，指向要刪除節點的指針置為 null。比如圖中的刪除節點 51。

第二種情況：如果要刪除的節點只有一個子節點（只有左子節點或者右子節點），我們只需要更新父節點中，指向要刪除節點的指針，讓它指向要刪除節點的子節點就可以了。比如圖中的刪除節點 35。

第三種情況：如果要刪除的節點有兩個子節點，這就比較複雜了。我們需要找到這個節點的右子樹中的最小節點，把它替換到要刪除的節點上。然後再刪除掉這個最小節點，因為最小節點肯定沒有左子節點（如果有左子結點，那就不是最小節點了），所以，我們可以應用上面兩條規則來刪除這個最小節點。比如圖中的刪除節點 88

前面兩種情況稍微簡單一些，第三種情況，我製作了一張動態圖，希望能對你有所幫助。

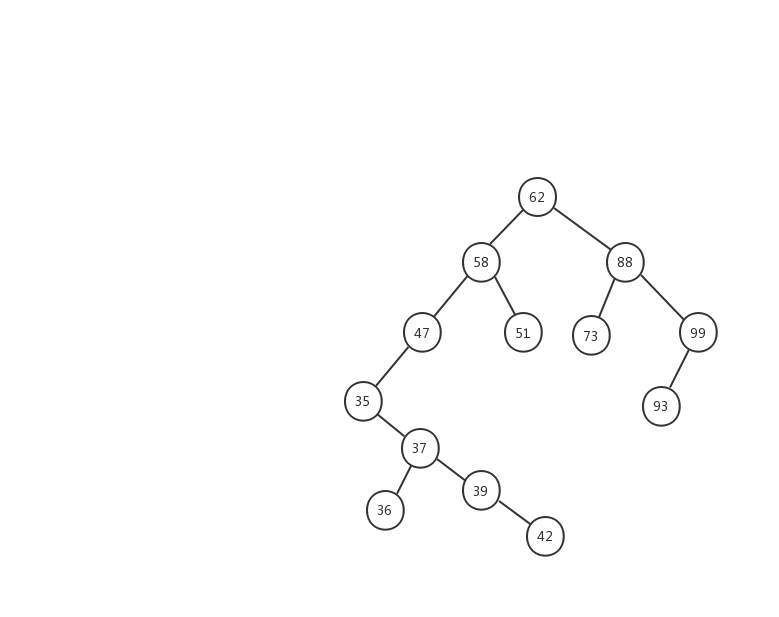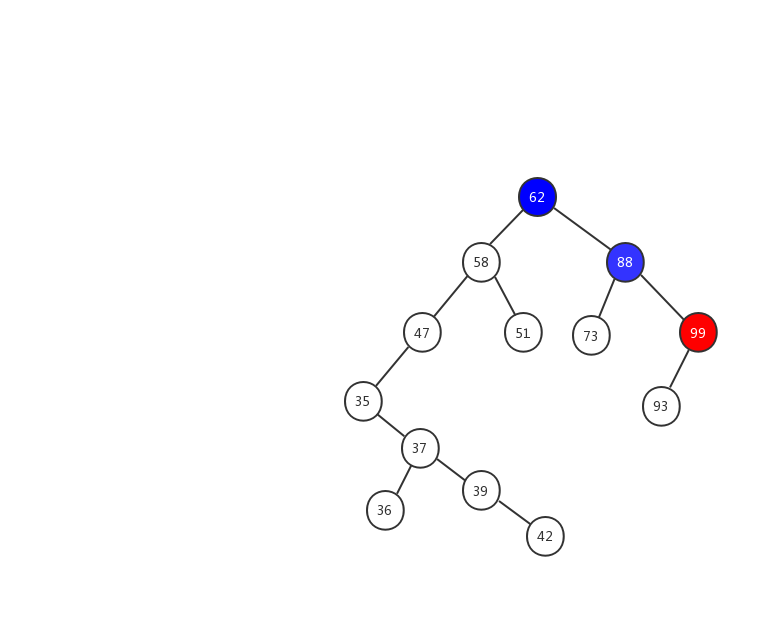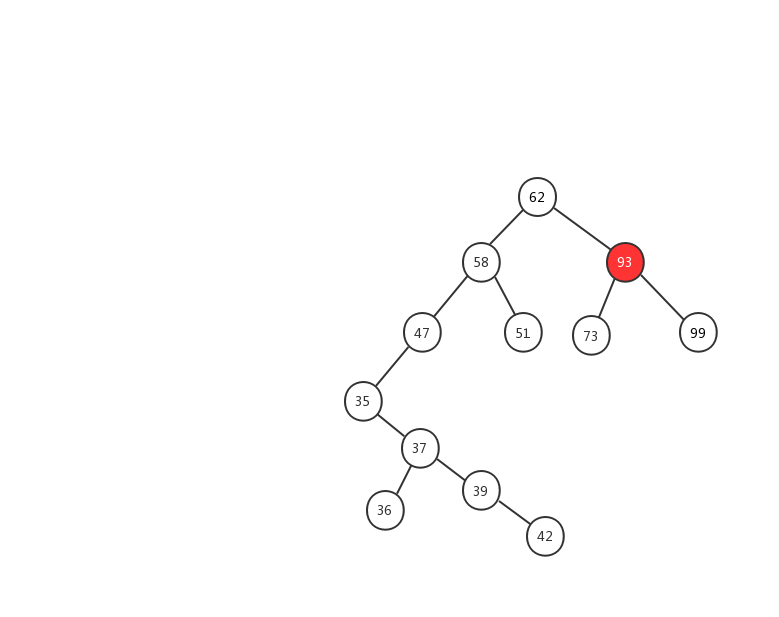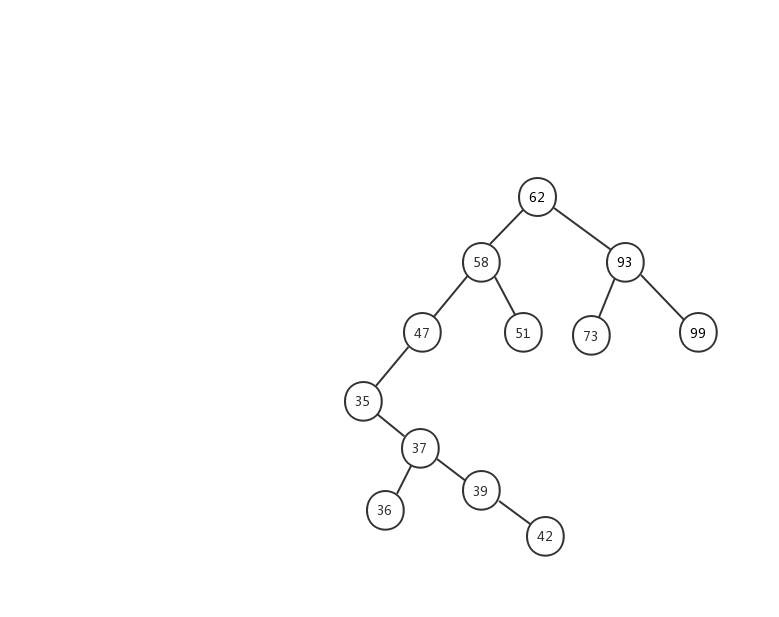
我們來看看二叉查找樹的刪除操作實現代碼

public void delete(int data) {      TreeNode p = tree; // p指向要刪除的節點，初始化指向根節點      TreeNode pp = null; // pp記錄的是p的父節點      while (p != null && p.data != data) {          pp = p;          if (data > p.data) p = p.right;          else p = p.left;      }      if (p == null) return; // 沒有找到        // 要刪除的節點有兩個子節點      if (p.left != null && p.right != null) { // 查找右子樹中最小節點          TreeNode minP = p.right;          TreeNode minPP = p; // minPP表示minP的父節點          while (minP.left != null) {              minPP = minP;              minP = minP.left;          }          p.data = minP.data; // 將minP的數據替換到p中          p = minP; // 下面就變成了刪除minP了          pp = minPP;      }        // 刪除節點是葉子節點或者僅有一個子節點      TreeNode child; // p的子節點      if (p.left != null) child = p.left;      else if (p.right != null) child = p.right;      else child = null;        if (pp == null) tree = child; // 刪除的是根節點      else if (pp.left == p) pp.left = child;      else pp.right = child;  }

我們上面了解了一些二叉查找樹的相關知識，由於二叉查找樹在極端情況下會退化成鏈表，例如每個節點都只有一個左節點，這是時間複雜度就變成了O(n)，為了避免這種情況，又出現了一種新的樹叫平衡二叉查找樹，由於本文篇幅有點長了，相信看到這裡的各位小夥伴已經有點疲憊了，關於平衡二叉查找樹的相關知識我就不在這裡介紹了。

最後

打個小廣告，金九銀十跳槽季，平頭哥給大家整理了一份較全面的 Java 學習資料，歡迎掃碼關注微信公眾號：「平頭哥的技術博文」領取，祝各位升職加薪。