數據競賽實戰(4)——交通事故理賠審核
- 2019 年 11 月 8 日
- 筆記
前言
1,背景介紹
在交通摩擦(事故)發生後,理賠員會前往現場勘察、採集信息,這些信息往往影響着車主是否能夠得到保險公司的理賠。訓練集數據包括理賠人員在現場對該事故方採集的36條信息,信息已經被編碼,以及該事故方最終是否獲得理賠。我們的任務是根據這36條信息預測該事故方沒有被理賠的概率
2,任務類型
入門二元分類模型
3,數據文件說明
train.csv 訓練集 文件大小為15.6MB
test.csv 預測集 文件大小為6.1MB
sample_submit.csv 提交示例 文件大小為1.4MB
4,數據變量說明
訓練集中共有200000條樣本,預測集中有80000條樣本。

5,評估方法
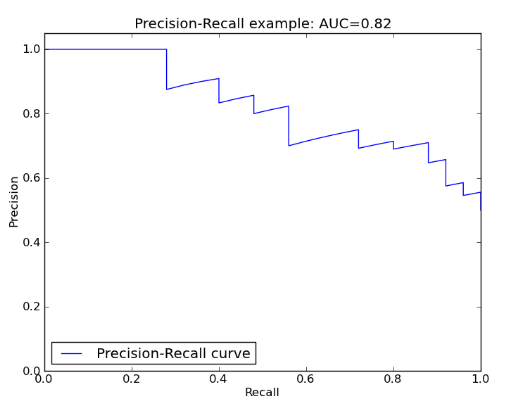
你的提交結果為每個測試樣本未通過審核的概率,也就是Evaluation為1的概率。評價方法為精度-召回曲線下面積(Precision-Recall AUC),以下簡稱PR-AUC。
PR-AUC的取值範圍是0到1。越接近1,說明模型預測的結果越接近真實結果。
5.1 精度和召回的定義和計算方式如下:
可以參考博文:機器學習筆記:常用評估方法
首先,我們先從混淆矩陣聊起,混淆矩陣是用來總結一個分類器結果的矩陣,對於K元分類,其實它就是一個 k * k 的表格,用來記錄分類器的預測結果。
對於最常見的二元分類來說,它的混淆矩陣是 2 * 2的,如下:
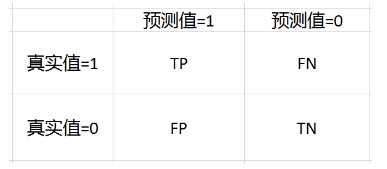
TP = True Positive = 真陽性; FP = False Positive = 假陽性
FN = False Negative = 假陰性; TN = True Negative = 真陰性
下面舉個例子
比如我們一個模型對15個樣本預測,然後結果如下:
預測值:1 1 1 1 1 0 0 0 0 0 1 1 1 0 1
真實值:0 1 1 0 1 1 0 0 1 0 1 0 1 0 0
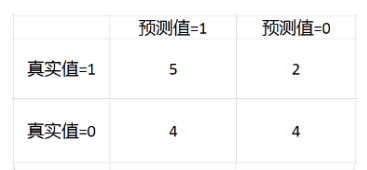
上面的就是混淆矩陣,混淆矩陣的這四個數值,經常被用來定義其他的一些度量。
準確度(Accuracy) = (TP+TN) / (TP+TN+FN+TN)
在上面的例子中,準確度 = (5+4) / 15 = 0.6
精度(precision, 或者PPV, positive predictive value) = TP / (TP + FP)
在上面的例子中,精度 = 5 / (5+4) = 0.556
召回(recall, 或者敏感度,sensitivity,真陽性率,TPR,True Positive Rate) = TP / (TP + FN)
在上面的例子中,召回 = 5 / (5+2) = 0.714
特異度(specificity,或者真陰性率,TNR,True Negative Rate) = TN / (TN + FP)
在上面的例子中,特異度 = 4 / (4+2) = 0.667
F1-值(F1-score) = 2*TP / (2*TP+FP+FN)
在上面的例子中,F1-值 = 2*5 / (2*5+4+2) = 0.625
5.2 精準率Precision,召回率Recall
精確率(正確率)和召回率是廣泛用於信息檢索和統計學分類領域的兩個度量值,用來評價結果的質量。其中精度是檢索出相關文檔樹與檢索出的文檔總數的比率,衡量的是檢索系統的查准率;召回率是指檢索出的相關文檔數和文檔庫中所有的相關文檔數的比率,衡量的是檢索系統的查全率。
一般來說,Precsion就是檢索出來的條目(比如:文檔,網頁等)有多少是準確的,Recall就是所有準確的條目有多少被檢索出來了,兩者定義如下:

精準度(又稱查准率)和召回率(又稱查全率)是一對矛盾的度量。一般來說,查准率高時,查全率往往偏低,而查全率高時,查准率又往往偏低,所以通常只有在一些簡單任務中,才可能使得查准率和查全率都很高。
5.3 PR-AUC的定義如下:
首先舉個例子:
比如100個測試樣本,根據我們的模型,我們得到了這100個點是被分為標籤1的概率y1, y2, y3,…y100、
下面我們需要閾值t,把概率轉化為標籤,如果 y_i 顯然,一個 t 的取值,對應着一組(精度,召回)。我們遍歷 t 所有的取值, 0, y1, y2, y3, … y100, 1。 我們就得到了102組(精度,召回)。
以召回為X軸,精度為Y軸,我們就可以在XOY坐標系中標出102個坐標點,把這102個點連成線,這個折線就稱為精度召回曲線。曲線與坐標軸圍成的面積就是精度-召回AUC。AUC越接近1,說明模型越好。
AUC是一種模型分類指標,且僅僅是二分類模型的評價指標。AUC是Area Under Curve(曲線下面積)的簡稱,那麼Curve就是ROC(Receiver Operating Characteristic),翻譯為“接受者操作特性曲線”。也就是說ROC是一條曲線,AUC是一個面積值。
ROC曲線應該盡量偏離參考線,越靠近左上越好。
AUC:ROC曲線下面積,參考面積為0.5,AUC應大於0.5,且偏離越多越好。
5.4 什麼是AUC?
AUC是ROC曲線所覆蓋的區域面積,顯然,AUC越大,分類器分類效果越好。
AUC =1 是完美分類器,採用這個預測模型時,不管設定什麼閾值都能得出完美預測。絕大多數預測的場合,不存在完美分類器。
0.5 < AUC < 1,優於隨機猜測,這個分類器(模型)妥善設置閾值的話,能有預測價值。
AUC = 0.5 , 和隨機猜想一樣,模型沒有預測價值。
AUC < 0.5,比隨機猜想還差,但只要總是反預測就行,這樣就由於隨機猜測。
AUC的物理意義:假設分類器的輸出是樣本屬於正類的score(置信度),則AUC的物理意義為:任意一對(正,負)樣本,正樣本的score大於負樣本的score的概率。
AUC的物理意義正樣本的預測結果大於負樣本的預測結果的概率。所以AUC反應的是分類器對樣本的排序能力。
另外值得注意的是:AUC對樣本是否均衡並不敏感,這也是不均衡樣本通常採用AUC評價分類器性能的一個原因。
5.5 PR-AUC的計算方法如下:
第一種方法就是:AUC為ROC曲線下的面積,那我們直接計算面積可得。面積為一個個小的梯形面積之和。計算的精度與閾值的精度有關。
第二種方法:根據AUC的物理意義,我們計算正樣本score大於負樣本的score的概率。取N* M(N為正樣本數,M為負樣本數)個二元組,比較score,最後得到AUC,時間複雜度為O(N*M)。
第三種方法:與第二種方法相似,直接計算正樣本score大於負樣本的概率。我們首先把所有樣本按照score排序,依次用rank表示他們,如最大score的樣本,rank = n(n=M+N),其次為 n-1。那麼對於正樣本中rank最大的樣本,rank_max,有M – 1個其他正樣本比他的score小。最後我們得到正樣本大於負樣本的概率的時間複雜度為 O(N+M)
from sklearn.metrics import roc_auc_score # y_test:實際的標籤, dataset_pred:預測的概率值。 roc_auc_score(y_test, dataset_pred)
使用sklearn.metrics.average_precision_score
>>> import numpy as np >>> from sklearn.metrics import average_precision_score >>> y_true = np.array([0, 0, 1, 1]) >>> y_predict = np.array([0.1, 0.4, 0.35, 0.8]) >>> average_precision_score(y_true, y_predict) 0.791666666
6,完整代碼,請移步小編的GitHub
傳送門:請點擊我
數據預處理
1,觀察數據有沒有缺失值
print(train.info()) <class 'pandas.core.frame.DataFrame'> RangeIndex: 10000 entries, 0 to 9999 Data columns (total 7 columns): city 10000 non-null int64 hour 10000 non-null int64 is_workday 10000 non-null int64 weather 10000 non-null int64 temp_1 10000 non-null float64 temp_2 10000 non-null float64 wind 10000 non-null int64 dtypes: float64(2), int64(5) memory usage: 547.0 KB None
我們可以看到,共有10000個觀測值,沒有缺失值。
2,觀察每個變量的基礎描述信息
print(train.describe()) city hour ... temp_2 wind count 10000.000000 10000.000000 ... 10000.000000 10000.000000 mean 0.499800 11.527500 ... 15.321230 1.248600 std 0.500025 6.909777 ... 11.308986 1.095773 min 0.000000 0.000000 ... -15.600000 0.000000 25% 0.000000 6.000000 ... 5.800000 0.000000 50% 0.000000 12.000000 ... 16.000000 1.000000 75% 1.000000 18.000000 ... 24.800000 2.000000 max 1.000000 23.000000 ... 46.800000 7.000000 [8 rows x 7 columns]
通過觀察可以得出一些猜測,如城市0 和城市1基本可以排除南方城市;整個觀測記錄時間跨度較長,還可能包含了一個長假期數據等等。
3,查看相關係數
(為了方便查看,絕對值低於0.2的就用nan替代)
corr = feature_data.corr() corr[np.abs(corr) < 0.2] = np.nan print(corr) city hour is_workday weather temp_1 temp_2 wind city 1.0 NaN NaN NaN NaN NaN NaN hour NaN 1.0 NaN NaN NaN NaN NaN is_workday NaN NaN 1.0 NaN NaN NaN NaN weather NaN NaN NaN 1.0 NaN NaN NaN temp_1 NaN NaN NaN NaN 1.000000 0.987357 NaN temp_2 NaN NaN NaN NaN 0.987357 1.000000 NaN wind NaN NaN NaN NaN NaN NaN 1.0
從相關性角度來看,用車的時間和當時的氣溫對借取數量y有較強的關係;氣溫和體感氣溫顯強正相關(共線性),這個和常識一致。
模型訓練及其結果展示
1,標杆模型:LASSO邏輯回歸模型
該模型預測結果結果的PR-AUC為:0.714644
# -*- coding: utf-8 -*- import pandas as pd from sklearn.linear_model import LogisticRegression # 讀取數據 train = pd.read_csv("train.csv") test = pd.read_csv("test.csv") submit = pd.read_csv("sample_submit.csv") # 刪除id train.drop('CaseId', axis=1, inplace=True) test.drop('CaseId', axis=1, inplace=True) # 取出訓練集的y y_train = train.pop('Evaluation') # 建立LASSO邏輯回歸模型 clf = LogisticRegression(penalty='l1', C=1.0, random_state=0) clf.fit(train, y_train) y_pred = clf.predict_proba(test)[:, 1] # 輸出預測結果至my_LASSO_prediction.csv submit['Evaluation'] = y_pred submit.to_csv('my_LASSO_prediction.csv', index=False)
2,標杆模型:隨機森林分類模型
該模型預測結果的PR-AUC為:0.850897
# -*- coding: utf-8 -*- import pandas as pd from sklearn.ensemble import RandomForestClassifier # 讀取數據 train = pd.read_csv("train.csv") test = pd.read_csv("test.csv") submit = pd.read_csv("sample_submit.csv") # 刪除id train.drop('CaseId', axis=1, inplace=True) test.drop('CaseId', axis=1, inplace=True) # 取出訓練集的y y_train = train.pop('Evaluation') # 建立隨機森林模型 clf = RandomForestClassifier(n_estimators=100, random_state=0) clf.fit(train, y_train) y_pred = clf.predict_proba(test)[:, 1] # 輸出預測結果至my_RF_prediction.csv submit['Evaluation'] = y_pred submit.to_csv('my_RF_prediction.csv', index=False)
我提交的結果:
![]()
這裡我嘗試了使用隨機森林進行關鍵特徵提取,然後對關鍵特徵進行模型訓練,發現效果不是很好,所以這裡就不貼特徵提取的代碼了。如果有需求,請參考我之前的博客。
KMeans 算法與交通事故理賠審核預測
K-Means 是基於劃分的聚類方法,他是數據挖掘十大算法之一。基於劃分的方法是將樣本集組成的矢量空間劃分成為多個區域,每個區域都存在一個樣本中心,通過建立映射關係,可以將所有樣本分類到其相應的中心。
1,經典的K-Means聚類算法步驟
- 1,初始化聚類中心
- 2,分配樣本到相近的聚類集合
- 3,根據步驟2的結果,更新聚類中心
- 4,若達到最大迭代步數或兩次迭代差小於設定的閾值則算法結束,否則重複步驟2.
經典的K-means算法在初始化聚類中心時採用的時隨機採樣的方式,不能保證得到期望的聚類結果,可以選擇重複訓練多個模型,選取其中表現最好的,但是有沒有更好的方法呢?David Arthur提出的 K-means++算法能夠有效地產生初始化的聚類中心。
首先隨機初始化一個聚類中心C1,然後通過迭代計算最大概率值X,將其加入到中心點中,重複該過程,直到選擇K個中心。
2,快速了解數據情況
顯示數據簡略信息,可以看到每列有多少非空的值,以及每列數據對應的數據類型。
本文數據對應的結果如下:
<class 'pandas.core.frame.DataFrame'> RangeIndex: 200000 entries, 0 to 199999 Data columns (total 37 columns): Q1 200000 non-null int64 Q2 200000 non-null int64 Q3 200000 non-null int64 Q4 200000 non-null int64 Q5 200000 non-null int64 Q6 200000 non-null int64 Q7 200000 non-null int64 Q8 200000 non-null int64 Q9 200000 non-null int64 Q10 200000 non-null int64 Q11 200000 non-null int64 Q12 200000 non-null int64 Q13 200000 non-null int64 Q14 200000 non-null int64 Q15 200000 non-null int64 Q16 200000 non-null int64 Q17 200000 non-null int64 Q18 200000 non-null int64 Q19 200000 non-null int64 Q20 200000 non-null int64 Q21 200000 non-null int64 Q22 200000 non-null int64 Q23 200000 non-null int64 Q24 200000 non-null int64 Q25 200000 non-null int64 Q26 200000 non-null int64 Q27 200000 non-null int64 Q28 200000 non-null int64 Q29 200000 non-null int64 Q30 200000 non-null int64 Q31 200000 non-null int64 Q32 200000 non-null int64 Q33 200000 non-null int64 Q34 200000 non-null int64 Q35 200000 non-null int64 Q36 200000 non-null int64 Evaluation 200000 non-null int64 dtypes: int64(37) memory usage: 56.5 MB None
想要了解特徵之間的相關性,可計算相關係數矩陣,然後可對某個特徵來排序
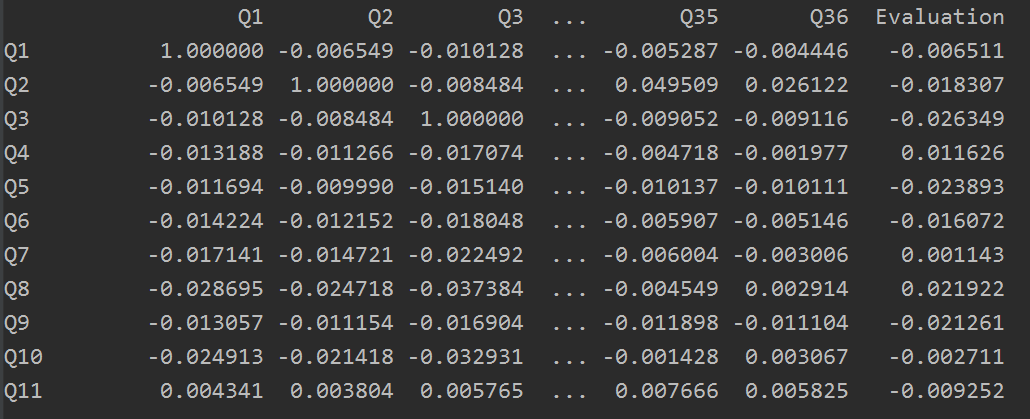
排序後結果如下:
Evaluation 1.000000 Q28 0.410700 Q30 0.324421 Q36 0.302709 Q35 0.224996 Q34 0.152743 Q32 0.049397 Q21 0.034897 Q33 0.032248 Q13 0.023603 Q8 0.021922 Q19 0.019694 Q20 0.013903 Q4 0.011626 Q27 0.004262 Q23 0.002898 Q7 0.001143 Q31 -0.000036 Q14 -0.000669 Q29 -0.002014 Q10 -0.002711 Q12 -0.005287 Q1 -0.006511 Q16 -0.007184 Q18 -0.007643 Q26 -0.008188 Q11 -0.009252 Q24 -0.010891 Q22 -0.011821 Q25 -0.012660 Q6 -0.016072 Q2 -0.018307 Q15 -0.019570 Q9 -0.021261 Q5 -0.023893 Q3 -0.026349 Q17 -0.028461 Name: Evaluation, dtype: float64
3,使用K-Means訓練模型
KMeans():n_clusters指要預測的有幾個類;init指初始化中心的方法,默認使用的是k-means++方法,而非經典的K-means方法的隨機採樣初始化,當然你可以設置為random使用隨機初始化;n_jobs指定使用CPU核心數,-1為使用全部CPU。
完整的代碼如下:
import pandas as pd traindata = pd.read_csv(r'data/train.csv') testdata = pd.read_csv(r'data/test.csv') # 去掉沒有意義的一列 traindata.drop('CaseId', axis=1, inplace=True) testdata.drop('CaseId', axis=1, inplace=True) # head() 默認顯示前5行數據,可指定顯示多行 # 例如 head(50)顯示前50行 # 查看每類有多少空值 # res = traindata.isnull().sum() # 顯示數據簡略信息,可以每列有多少非空的值,以及每列數據對應的數據類型 # res = traindata.info() # 以圖的形式,快速了解數據 # ~hist():繪製直方圖,參數figsize可指定輸出圖片的尺寸。 # traindata.hist(figsize=(20, 20)) # # 想要了解特徵之間的相關性,可計算相關係數矩陣,然後可對某個特徵來排序 # corr_matrix = traindata.corr() # # ascending=False 表示降序排列 # corr_matrix = corr_matrix['Evaluation'].sort_values(ascending=False) # print(corr_matrix) # 從訓練集中分類標籤 y = traindata['Evaluation'] traindata.drop('Evaluation', axis=1, inplace=True) from sklearn.cluster import KMeans clf = KMeans(n_clusters=2, init='k-means++', n_jobs=-1) clf.fit(traindata, y) y_pred = clf.predict(testdata) # 保存預測的結果 submitData = pd.read_csv(r'data/sample_submit.csv') submitData['Evaluation'] = y_pred submitData.to_csv("KMeans.csv", index=False)
結果如下:0.485968

K-means算法是數據挖掘的十大經典算法之一,但實際中如果想要得到滿意的效果,還是非常難的,這裡做一個嘗試,確實是不行的。
4,自己使用XGBoost訓練
直接訓練,代碼如下:
import pandas as pd import numpy as np from sklearn.model_selection import train_test_split import xgboost as xgb from sklearn.metrics import accuracy_score traindata = pd.read_csv(r'data/train.csv') testdata = pd.read_csv(r'data/test.csv') # 去掉沒有意義的一列 traindata.drop('CaseId', axis=1, inplace=True) testdata.drop('CaseId', axis=1, inplace=True) # 從訓練集中分類標籤 trainlabel = traindata['Evaluation'] traindata.drop('Evaluation', axis=1, inplace=True) traindata1, testdata1, trainlabel1 = traindata.values, testdata.values, trainlabel.values # 數據集分割 X_train, X_test, y_train, y_test = train_test_split(traindata1, trainlabel1, test_size=0.3, random_state=123457) # 訓練模型 model = xgb.XGBClassifier(max_depth=5, learning_rate=0.1, gamma=0.1, n_estimators=160, silent=True, objective='binary:logistic', nthread=4, seed=27, colsample_bytree=0.8) model.fit(X_train, y_train) # 對測試集進行預測 y_pred = model.predict(X_test) # 計算準確率 accuracy = accuracy_score(y_test, y_pred) print('accuracy:%2.f%%' % (accuracy * 100)) #查看AUC評價標準 # from sklearn import metrics ##必須二分類才能計算 # print("AUC Score (Train): %f" % metrics.roc_auc_score(y_test, y_pred)) def run_predict(): y_pred_test = model.predict_proba(testdata1)[:, 1] # 保存預測的結果 submitData = pd.read_csv(r'data/sample_submit.csv') submitData['Evaluation'] = y_pred_test submitData.to_csv("xgboost.csv", index=False) run_predict()
結果如下:

然後對XGBoost進行調參,調參結果如下:
這裡直接展示了模型的最佳參數:
XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1, colsample_bytree=0.6, gamma=0.3, learning_rate=0.1, max_delta_step=0, max_depth=6, min_child_weight=4, missing=None, n_estimators=1000, n_jobs=1, nthread=4, objective='binary:logistic', random_state=0, reg_alpha=1, reg_lambda=1, scale_pos_weight=1, seed=27, silent=True, subsample=0.9)
然後運行,得到的結果如下:

當然相比較之前的xgboost,結果提高了一些。
到目前為止,就做這些嘗試吧,看來xgboost還真是解題利器。有時間的話,繼續嘗試其他算法,那這些簡單的題,目的是繼續嘗試應用自己學到的算法。