Java 內功修鍊 之 數據結構與算法(一)
一、基本認識
1、數據結構與算法的關係?
(1)數據結構(data structure):
數據結構指的是 數據與數據 之間的結構關係。比如:數組、隊列、哈希、樹 等結構。
(2)算法:
算法指的是 解決問題的步驟。
(3)兩者關係:
程序 = 數據結構 + 算法。
解決問題可以有很多種方式,不同的算法實現 會得到不同的結果。正確的數據結構 是 好算法的基礎(算法好壞取決於 如何利用合適的數據結構去 處理數據、解決問題)。
(4)數據結構動態演示地址:
//www.cs.usfca.edu/~galles/visualization/Algorithms.html
2、數據結構分類?
(1)分類:
數據結構 可以分為 兩種:線性數據結構、非線性數據結構。
(2)線性數據結構:
線性數據結構指的是 數據元素之間存在一對一的線性關係。比如:一維數組、鏈表、隊列、棧。
其又可以分為:
順序存儲結構:指的是 使用一組地址連續的存儲單元 存儲數據元素 的結構,其每個元素節點僅用於 保存數據元素。比如:一維數組。
鏈式存儲結構:指的是 可使用一組地址不連續的存儲單元 存儲數據元素 的結構,其每個元素節點 保存數據元素 以及 相鄰數據元素的地址 信息。比如:鏈表。
(3)非線性數據結構:
非線性數據結構指的是 數據元素之間存在 一對多、多對多 的關係。比如:二維數組、多維數組、樹、圖 等。
3、時間複雜度、空間複雜度
(1)分析多個算法執行時間:
事前估算時間:程序運行前,通過分析某個算法的時間複雜度來判斷算法解決問題是否合適。
事後統計時間:程序運行後,通過計算程序運行時間來判斷(容易被計算機硬件、軟件等影響)。
註:
一般分析算法都是採用 事前估算時間,即估算分析 算法的 時間複雜度。
(2)時間頻度、時間複雜度:
時間頻度( T(n) ):
一個算法中 語句執行的次數 稱為 語句頻度 或者 時間頻度,記為 T(n)。
通常 一個算法花費的時間 與 算法中 語句的執行次數 成正比,即 某算法語句執行次數多,其花費時間就長。
時間複雜度( O(f(n)) ):
存在某個輔助函數 f(n),當 n 接近無窮大時,若 T(n) / f(n) 的極限值為不等於零的常數,則稱 f(n) 為 T(n) 的同數量級函數,記為 T(n) = O(f(n)),稱 O(f(n)) 為算法的漸進時間複雜度,簡稱 時間複雜度。
(3)通過 時間頻度( T(n) )推算 時間複雜度 ( O(f(n)) ):
對於一個 T(n) 表達式,比如: T(n) = an^2 + bn + c,其推算為 O(n) 需要遵循以下規則:
rule1:使用常數 1 替代表達式中的常數,若表達式存在高階項,則忽略常數項。
即:若 T(n) = 8,則其時間複雜度為 O(1)。若 T(n) = n^2 + 8,則其時間複雜度為 O(n^2)。
rule2:只保留最高階項,忽略所有低次項。
即:T(n) = 3n^2 + n^4 + 3n,其時間複雜度為 O(n^4)。
rule3:去除最高階項的係數。
即:T(n) = 3n^2 + 4n^3,其時間複雜度為 O(n^3)。
註:
T(n) 表達式不同,但是其對應的時間複雜度可能相同。
比如:T(n) = n^2 + n 與 T(n) = 3n^2 + 1 的時間複雜度均為 O(n^2)。
(4)常見時間複雜度
【常見時間複雜度(由小到大排序如下):】 O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(n^k) < O(2^n) 註: 時間複雜度越大,算法執行效率越低。 【常數階 O(1) :】 算法複雜度 與 問題規模無關。 比如: int a = 1; int b = 2; int c = a + b; 分析: 代碼中不存在循環、遞歸等結構,其時間複雜度即為 O(1)。 【對數階 O(logn) :】 算法複雜度 與 問題規模成對數關係。 比如: int i = 1; while(i < n) { i*=2; // 不斷乘 2 } 分析: 上述代碼中存在循環,設循環執行次數為 x,則循環退出條件為 2^x >= n。 從而推算出 x = logn,此時 log 以 2 為底,即時間複雜度為 O(logn)。 【線性階 O(n) :】 算法複雜度 與 問題規模成線性關係。 比如: for(int i = 0; i < n; i++) { System.out.println(i); } 分析: 代碼中存在循環,且循環次數為 n,即時間頻度為 T(n),從而時間複雜度為 O(n)。 【線性對數階 O(nlogn) :】 算法複雜度 與 問題規模成線性對數關係(循環嵌套)。 比如: for(int j = 0; j < n; j++) { int i = 1; while(i < n) { i*=2; // 不斷乘 2 } } 分析: 代碼中循環嵌套,完成 for 循環需要執行 n 次,每次均執行 while 循環 logn 次, 即總時間頻度為 T(nlogn), 從而時間複雜度為 O(nlogn)。 【平方階 O(n^2) :】 算法複雜度 與 問題規模成平方關係(循環嵌套)。 比如: for(int i = 0; i < n; i++) { for(int j = 0; j < n; j++) { System.out.println(i + j); } } 分析: 代碼中循環嵌套,總時間頻度為 T(n*n),即時間複雜度為 O(n^2) 【立方階 O(n^3) 、k 次方階 O(n^k) :】 類似於平方階 O(n^2),只是循環嵌套的層數更多了。 O(n^3) 表示三層循環。O(n^K) 表示四層循環。 【指數階 O(2^n) :】 算法複雜度 與 問題規模成指數關係(循環嵌套)。 這個算法的執行效率非常糟糕,一般都不考慮。 比如: int n = 3; for (int i = 0; i < Math.pow(2, n); i++) { System.out.println(i); } 分析: 上面循環,總時間頻度為 T(2^n),即時間複雜度為 O(2^n)。
(5)空間複雜度
空間複雜度 指的是算法所需耗費的存儲空間。與時間複雜度類似,但其關注的是算法執行所需佔用的臨時空間(非語句執行次數)。
一般算法分析更看重 時間複雜度,即保證程序執行速度快,比如:緩存 就是空間換時間。
二、基本數據結構以及代碼實現
1、稀疏數組(Sparse Array)
(1)什麼是稀疏數組?
當數組中 值為 0 的元素 大於 非 0 元素 且 非 0 元素 分佈無規律時,可以使用 稀疏數組 來表示該數組,其將一個大數組整理、壓縮成一個小數組,用於節約磁盤空間。
註:
不一定必須為 值為 0 的元素,一般 同一元素在數組中過多時即可。
使用 稀疏數組 的目的是為了 壓縮數組結構、節約磁盤空間(比如:一個二維數組 a[10][10] 可以存儲 100 個元素,但是其只存儲了 3 個元素後,那麼將會有 97 個空間被閑置,此時可以將 二維數組 轉為 稀疏數組 存儲,其最終轉換成 b[4][3] 數組進行保存,即從 a[10][10] 的數組 壓縮到 b[4][3],從而減少空間浪費)。
【舉例:】 定義二維數組 a[4][5],並存儲 3 個值如下: 0 0 0 0 0 0 1 0 2 0 0 0 0 0 0 0 0 1 0 0 此時,數組中元素為 0 的個數大於 非 0 元素個數,所以可以作為 稀疏數組 處理。 換種方式,比如 將 0 替換成 5 如下,也可以視為 稀疏數組 處理。 5 5 5 5 5 5 1 5 2 5 5 5 5 5 5 5 5 1 5 5
(2)二維數組轉為稀疏數組:
【如何處理:】 Step1:先記錄數組 有幾行幾列,有多少個不同的值。 Step2:將不同的值 的元素 的 行、列、值 記錄在一個 小規模的 數組中,從而將 大數組 縮減成 小數組。 【舉例:】 原二維數組如下: 0 0 0 0 0 0 1 0 2 0 0 0 0 0 0 0 0 1 0 0 經過處理後變為 稀疏數組 如下: 行 列 值 4 5 3 // 首先記錄原二維數組 有 幾行、幾列、幾個不同值 1 1 1 // 表示原二維數組中 a[1][1] = 1 1 3 2 // 表示原二維數組中 a[1][3] = 2 3 2 1 // 表示原二維數組中 a[3][2] = 1 可以看到,原二維數組 a[4][5] 轉為 稀疏數組 b[4][3],空間得到利用、壓縮。
(3)二維數組、稀疏數組 互相轉換實現
【二維數組 轉 稀疏數組:】 Step1:遍歷原始二維數組,得到 有效數據 個數 num。 Step2:根據有效數據個數創建 稀疏數組 a[num + 1][3]。 Step3:將原二維數組中有效數據存儲到 稀疏數組中。 註: 稀疏數組有 三列:分別為:行、 列、 值。 稀疏數組 第一行 存儲的為 原二維數組的行、列 以及 有效數據個數。其餘行存儲 有效數據所在的 行、列、值。 所以數組定義為 [num + 1][3] 【稀疏數組 轉 二維數組:】 Step1:讀取 稀疏數組 第一行數據並創建 二維數組 b[行][列]。 Step2:讀取其餘行,並賦值到新的二維數組中。 【代碼實現:】 package com.lyh.array; import java.util.HashMap; import java.util.Map; public class SparseArray { public static void main(String[] args) { // 創建原始 二維數組,定義為 4 行 10 列,並存儲 兩個 元素。 int[][] arrays = new int[4][10]; arrays[1][5] = 8; arrays[2][3] = 7; // 遍歷輸出原始 二維數組 System.out.println("原始二維數組如下:"); showArray(arrays); // 二維數組 轉 稀疏數組 System.out.println("\n二維數組 轉 稀疏數組如下:"); int[][] sparseArray = arrayToSparseArray(arrays); showArray(sparseArray); // 稀疏數組 再次 轉為 二維數組 System.out.println("\n稀疏數組 轉 二維數組如下:"); int[][] sparseToArray = sparseToArray(sparseArray); showArray(sparseToArray); } /** * 二維數組 轉 稀疏數組 * @param arrays 二維數組 * @return 稀疏數組 */ public static int[][] arrayToSparseArray(int[][] arrays) { // count 用於記錄有效數據個數 int count = 0; // HashMap 用於保存有效數據(把 行,列 用逗號分隔拼接作為 key,值作為 value) Map<String, Integer> map = new HashMap<>(); // 遍歷得到有效數據、以及總個數 for (int i = 0; i < arrays.length; i++) { for (int j = 0; j < arrays[i].length; j++) { if (arrays[i][j] != 0) { count++; map.put(i + "," + j, arrays[i][j]); } } } // 根據有效數據總個數定義 稀疏數組,並賦值 int[][] result = new int[count + 1][3]; result[0][0] = arrays.length; result[0][1] = arrays[0].length; result[0][2] = count; // 把有效數據從 HashMap 中取出 並放到 稀疏數組中 for(Map.Entry<String, Integer> entry : map.entrySet()) { String[] temp = entry.getKey().split(","); result[count][0] = Integer.valueOf(temp[0]); result[count][1] = Integer.valueOf(temp[1]); result[count][2] = entry.getValue(); --count; } return result; } /** * 遍歷輸出 二維數組 * @param arrays 二維數組 */ public static void showArray(int[][] arrays) { for (int[] a : arrays) { for (int data : a) { System.out.print(data + " "); } System.out.println(); } } /** * 稀疏數組 轉 二維數組 * @param arrays 稀疏數組 * @return 二維數組 */ public static int[][] sparseToArray(int[][] arrays) { int[][] result = new int[arrays[0][0]][arrays[0][1]]; for (int i = 1; i < arrays.length; i++) { result[arrays[i][0]][arrays[i][1]] = arrays[i][2]; } return result; } } 【輸出結果:】 原始二維數組如下: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 二維數組 轉 稀疏數組如下: 4 10 2 1 5 8 2 3 7 稀疏數組 轉 二維數組如下: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2、隊列(Queue)、環形隊列
(1)什麼是隊列?
隊列指的是一種 受限的、線性的數據結構,其僅允許在 一端進行插入操作(隊尾插入,rear),且在另一端進行 刪除操作(隊首刪除,front)。
隊列可以使用 數組 或者 鏈表 實現(一般採用數組實現,僅在首尾增刪,效率比鏈表高)。
其遵循 先進先出(First In First Out,FIFO) 原則,即先存入 隊列的值 先取出。
【使用 數組實現 隊列:】 需要注意三個值: maxSize: 表示隊列最大容量。 front: 表示隊列頭元素下標(指向隊列頭部的第一個元素的前一個位置),初始值為 -1. rear: 表示隊列尾元素下標(指向隊列尾部的最後一個元素),初始值為 -1。 臨界條件: front == rear 時,表示隊列為 空。 rear == maxSize - 1 時,表示隊列已滿。 rear - front, 表示隊列的存儲元素的個數。 數據進入隊列時: front 不動,rear++。 數據出隊列時: rear 不動,front++。
如下圖:
紅色表示入隊操作,rear 加 1。
黃色表示出隊操作,front 加 1。
每次入隊,向當前實際數組尾部添加元素,每次出隊,從當前實際數組頭部取出元素,符合 先進先出原則。

可以很明顯的看到,如果按照這種方式實現隊列,黃色區域的空間將不會被再次使用,即此時的隊列是一次性的。
那麼如何重複利用 黃色區域的空間?可以採用 環形隊列實現(看成一個環來實現)。
環形隊列在 上面隊列的基礎上稍作修改,當成環處理(數據首尾相連,可以通過 % 進行取模運算實現),核心是考慮 隊列 什麼時候為空,什麼時候為滿。
一般採用 犧牲一個 數組空間 作為判斷當前隊列是否已滿的條件。
【使用 數組 實現環形隊列:(此處僅供參考)】 需要注意三個值: maxSize: 表示隊列最大容量。 front: 表示隊列頭元素下標(指向隊列頭部的第一個元素),初始值為 0。 rear: 表示隊列尾元素下標(指向隊列尾部的最後一個元素的後一個位置),初始值為 0。 臨界條件: front == rear 時,表示隊列為 空。 (rear + 1) % maxSize == front 時,表示隊列已滿。 (rear - front + maxSize) % maxSize, 表示隊列的存儲元素的個數。 數據進入隊列時: front 不動,rear = (rear + 1) % maxSize。 數據出隊列時: rear 不動,front = (front + 1) % maxSize。

(2)使用數組實現隊列
【代碼實現:】 package com.lyh.queue; public class ArrayQueue<E> { private int maxSize; // 隊列最大容量 private int front; // 隊列首元素 private int rear; // 隊列尾元素 private Object[] queue; // 存儲隊列 /** * 構造初始隊列 * @param maxSize 隊列最大容量 */ public ArrayQueue(int maxSize) { this.maxSize = maxSize; queue = new Object[maxSize]; front = -1; rear = -1; } /** * 添加數據進入隊列 * @param e 待入數據 */ public void addQueue(E e) { if (isFull()) { System.out.println("隊列已滿"); return; } // 隊列未滿時,添加數據,rear 向後移動一位 queue[++rear] = e; } /** * 從隊列中取出數據 * @return 待取數據 */ public E getQueue() { if (isEmpty()) { System.out.println("隊列已空"); return null; } // 隊列不空時,取出數據,front 向後移動一位 return (E)queue[++front]; } /** * 輸出當前隊列所有元素 */ public void showQueue() { if (isEmpty()) { System.out.println("隊列已空"); return; } System.out.print("當前隊列存儲元素總個數為:" + getSize() + " 當前隊列為:"); for(int i = front + 1; i <= rear; i++) { System.out.print(queue[i] + " "); } System.out.println(); } /** * 獲取當前隊列實際大小 * @return 隊列實際存儲數據數量 */ public int getSize() { return rear - front; } /** * 判斷隊列是否為空 * @return true 為空 */ public boolean isEmpty() { return front == rear; } /** * 判斷隊列是否已滿 * @return true 已滿 */ public boolean isFull() { return rear == maxSize - 1; } public static void main(String[] args) { // 創建隊列 ArrayQueue<Integer> arrayQueue = new ArrayQueue<>(6); // 添加數據 arrayQueue.addQueue(10); arrayQueue.addQueue(8); arrayQueue.addQueue(9); arrayQueue.showQueue(); // 取數據 System.out.println(arrayQueue.getQueue()); System.out.println(arrayQueue.getQueue()); arrayQueue.showQueue(); } } 【輸出結果:】 當前隊列存儲元素總個數為:3 當前隊列為:10 8 9 10 8 當前隊列存儲元素總個數為:1 當前隊列為:9
(3)使用數組實現環形隊列
【代碼實現:】 package com.lyh.queue; public class ArrayCircleQueue<E> { private int maxSize; // 隊列最大容量 private int front; // 隊列首元素 private int rear; // 隊列尾元素 private Object[] queue; // 存儲隊列 /** * 構造初始隊列 * @param maxSize 隊列最大容量 */ public ArrayCircleQueue(int maxSize) { this.maxSize = maxSize; queue = new Object[maxSize]; front = 0; rear = 0; } /** * 添加數據進入隊列 * @param e 待入數據 */ public void addQueue(E e) { if (isFull()) { System.out.println("隊列已滿"); return; } // 隊列未滿時,添加數據,rear 向後移動一位 queue[rear] = e; rear = (rear + 1) % maxSize; } /** * 從隊列中取出數據 * @return 待取數據 */ public E getQueue() { if (isEmpty()) { System.out.println("隊列已空"); return null; } // 隊列不空時,取出數據,front 向後移動一位 E result = (E)queue[front]; front = (front + 1) % maxSize; return result; } /** * 輸出當前隊列所有元素 */ public void showQueue() { if (isEmpty()) { System.out.println("隊列已空"); return; } System.out.print("當前隊列存儲元素總個數為:" + getSize() + " 當前隊列為:"); for(int i = front; i < front + getSize(); i++) { System.out.print(queue[i] + " "); } System.out.println(); } /** * 獲取當前隊列實際大小 * @return 隊列實際存儲數據數量 */ public int getSize() { return (rear - front + maxSize) % maxSize; } /** * 判斷隊列是否為空 * @return true 為空 */ public boolean isEmpty() { return front == rear; } /** * 判斷隊列是否已滿 * @return true 已滿 */ public boolean isFull() { return (rear + 1) % maxSize == front; } public static void main(String[] args) { // 創建隊列 ArrayCircleQueue<Integer> arrayQueue = new ArrayCircleQueue<>(3); // 添加數據 arrayQueue.addQueue(10); arrayQueue.addQueue(8); arrayQueue.addQueue(9); arrayQueue.showQueue(); // 取數據 System.out.println(arrayQueue.getQueue()); System.out.println(arrayQueue.getQueue()); arrayQueue.showQueue(); } } 【輸出結果:】 隊列已滿 當前隊列存儲元素總個數為:2 當前隊列為:10 8 10 8 隊列已空
3、鏈表(Linked list)– 單鏈表 以及 常見筆試題
(1)什麼是鏈表?
鏈表指的是 物理上非連續、非順序,但是 邏輯上 有序 的 線性的數據結構。
鏈表 由 一系列節點 組成,節點之間通過指針相連,每個節點只有一個前驅節點、只有一個後續節點。節點包含兩部分:存儲數據元素的數據域 (data)、存儲下一個節點的指針域 (next)。
可以使用 數組、指針 實現。比如:Java 中 ArrayList 以及 LinkedList。
(2)單鏈表實現?
單鏈表 指的是 單向鏈表,首節點沒有前驅節點,尾節點沒有後續節點。只能沿着一個方向進行 遍歷、獲取數據的操作(即某個節點無法獲取上一個節點的數據)。
可參考://www.cnblogs.com/l-y-h/p/11385295.html
註:
頭節點(非必須):僅用於作為鏈表起點,放在鏈表第一個節點前,無實際意義。
首節點:指鏈表第一個節點,即頭節點後面的第一個節點。
頭節點是非必須的,使用頭節點是方便操作鏈表而設立的。如下代碼實現採用 頭節點 方式實現。
【模擬 指針形式 實現 單鏈表:】 模擬節點: 節點包括 數據域(保存數據) 以及 指針域(指向下一個節點)。 class Node<E> { E data; // 數據域,存儲節點數據 Node next; // 指針域,指向下一個節點 public Node(E data) { this.data = data; } public Node(E data, Node<E> next) { this.data = data; this.next = next; } } 【增刪節點:】 直接添加節點 A 到鏈表末尾: 先得遍歷得到最後一個節點 B 所在位置,條件為: B.next == null, 然後將最後一個節點 B 的 next 指向該節點, 即 B.next = A。 向指定位置插入節點: 比如: A->B 中插入 C, 即 A->C->B,此時,先讓 C 指向 B,再讓 A 指向 C。 即 C.next = A.next; // 此時 A.next = B A.next = C; 直接刪除鏈表末尾節點: 先遍歷到倒數第二個節點 C 位置,條件為:C.next.next == null; 然後將其指向的下一個節點置為 null 即可,即 C.next = null。 刪除指定位置的節點: 比如: A->C->B 中刪除 C,此時,直接讓 A 指向 B。 即: A.next = C.next;

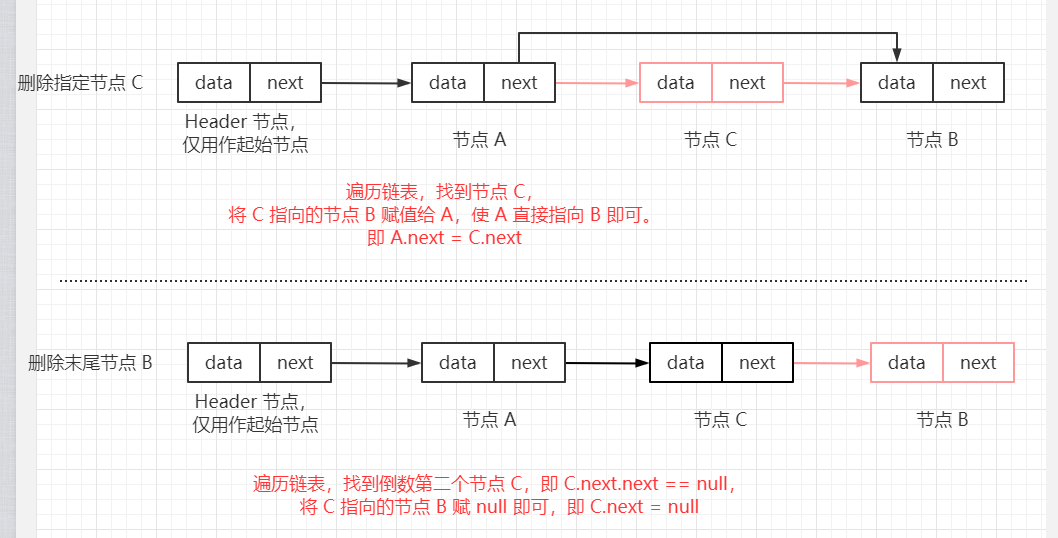
【代碼實現:】 package com.lyh.com.lyh.linkedlist; public class SingleLinkedList<E> { private int size; // 用於保存鏈表實際長度 private Node<E> header; // 用於保存鏈表頭節點,僅用作 起點,不存儲數據。 public SingleLinkedList(Node<E> header) { this.header = header; } /** * 在鏈表末尾添加節點 * @param data 節點數據 */ public void addLastNode(E data) { Node<E> newNode = new Node<>(data); // 根據數據創建一個 新節點 Node<E> temp = header; // 使用臨時變量保存頭節點,用於輔助遍歷鏈表 // 遍歷鏈表 while(temp.next != null) { temp = temp.next; } // 在鏈表末尾添加節點,鏈表長度加 1 temp.next = newNode; size++; } /** * 在鏈表末尾添加節點 * @param newNode 節點 */ public void addLastNode(Node<E> newNode) { Node<E> temp = header; // 使用臨時變量保存頭節點,用於輔助遍歷鏈表 // 遍歷鏈表 while(temp.next != null) { temp = temp.next; } // 在鏈表末尾添加節點,鏈表長度加 1 temp.next = newNode; size++; } /** * 在鏈表指定位置 插入節點 * @param node 待插入節點 * @param index 指定位置(1 ~ n, 1 表示第一個節點位置) */ public void insert(Node<E> node, int index) { Node<E> temp = header; // 使用臨時變量保存頭節點,用於輔助遍歷鏈表 // 節點越界則拋出異常 if (index < 1 || index > size) { throw new IndexOutOfBoundsException("Index: " + index + ", Size: " + size); } // 若節點為鏈表末尾,則調用 末尾添加 節點的方法 if (index == size) { addLastNode(node); return; } // 若節點不是鏈表末尾,則遍歷找到插入位置 while(index != 1) { temp = temp.next; index--; } // A -> B 變為 A -> C -> B, 即 A.next = B 變為 C.next = A.next, A.next = C,即 A 指向 C,C 指向 B。 node.next = temp.next; temp.next = node; size++; } /** * 返回鏈表長度 * @return 鏈表長度 */ public int size() { return size; } /** * 輸出鏈表 */ public void showList() { Node<E> temp = header.next; // 使用臨時變量保存第一個節點,用於輔助遍歷鏈表 if (size == 0) { System.out.println("當前鏈表為空"); return; } // 鏈表不為空時遍歷鏈表 System.out.print("當前鏈表長度為: " + size + " 當前鏈表為: "); while(temp != null) { System.out.print(temp + " ===> "); temp = temp.next; } System.out.println(); } /** * 刪除最後一個節點 */ public void deleteLastNode() { Node<E> temp = header; // 使用臨時變量保存頭節點,用於遍歷鏈表 if (size == 0) { System.out.println("當前鏈表為空,無需刪除"); return; } while(temp.next.next != null) { temp = temp.next; } temp.next = null; size--; } /** * 刪除指定位置的元素 * @param index 指定位置(1 ~ n, 1 表示第一個節點位置) */ public void delete(int index) { Node<E> temp = header; // 使用臨時變量保存頭節點,用於輔助遍歷鏈表 // 節點越界則拋出異常 if (index < 1 || index > size) { throw new IndexOutOfBoundsException("Index: " + index + ", Size: " + size); } // 若節點為鏈表末尾,則調用 末尾刪除 節點的方法 if (index == size) { deleteLastNode(); return; } // 遍歷鏈表,找到刪除位置 while(index != 1) { index--; temp = temp.next; } // A -> C -> B 變為 A -> B,即 A.next = C, C.next = B 變為 A.next = C.next,即 A 直接指向 B temp.next = temp.next.next; size--; } public static void main(String[] args) { // 創建一個單鏈表 SingleLinkedList<String> singleLinkedList = new SingleLinkedList(new Node("Header")); // 輸出,此時鏈表為空 singleLinkedList.showList(); System.out.println("======================================="); // 給鏈表添加數據 singleLinkedList.addLastNode("Java"); singleLinkedList.addLastNode(new Node<>("JavaScript")); singleLinkedList.insert(new Node<>("Phthon"), 1); singleLinkedList.insert(new Node<>("C"), 3); // 輸出鏈表 singleLinkedList.showList(); System.out.println("======================================="); // 刪除鏈表數據 singleLinkedList.deleteLastNode(); singleLinkedList.delete(2); // 輸出鏈表 singleLinkedList.showList(); System.out.println("======================================="); } } class Node<E> { E data; // 數據域,存儲節點數據 Node<E> next; // 指針域,指向下一個節點 public Node(E data) { this.data = data; } public Node(E data, Node<E> next) { this.data = data; this.next = next; } @Override public String toString() { return "Node{ data = " + data + " }"; } } 【輸出結果:】 當前鏈表為空 ======================================= 當前鏈表長度為: 4 當前鏈表為: Node{ data = Phthon } ===> Node{ data = Java } ===> Node{ data = JavaScript } ===> Node{ data = C } ===> ======================================= 當前鏈表長度為: 2 當前鏈表為: Node{ data = Phthon } ===> Node{ data = JavaScript } ===> =======================================
(3)常見的單鏈表筆試題
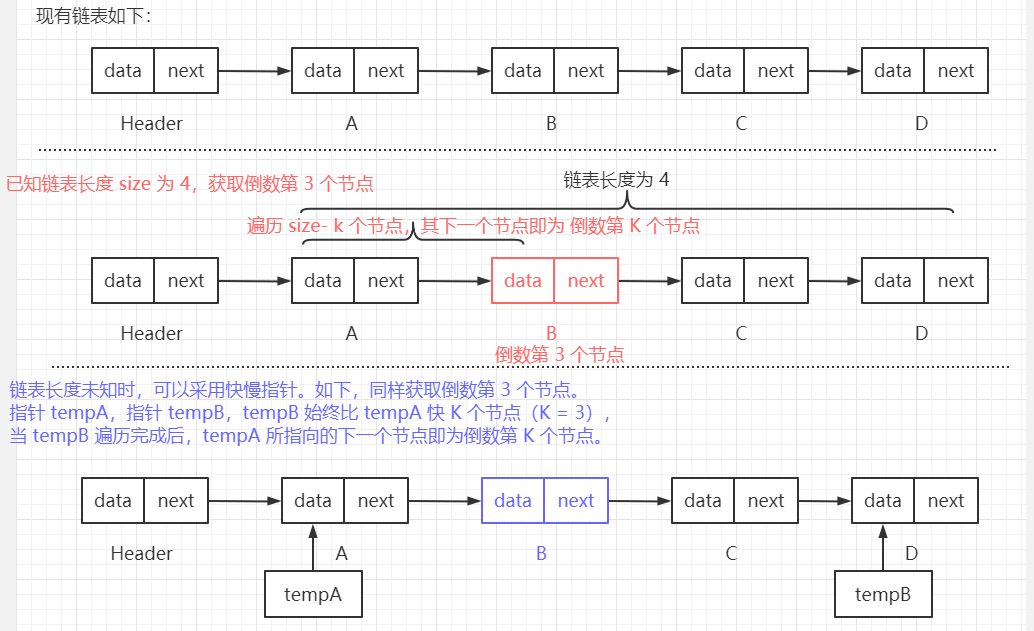
【筆試題一:】 找到當前鏈表中倒數 第 K 個節點。 【筆試題一解決思路:】 思路一: 鏈表長度 size 可知時,則可以遍歷 size - k 個節點,從而找到倒數第 K 個節點。 當然 size 可以通過遍歷一遍鏈表得到,這會消耗時間。 思路二: 鏈表長度 size 未知時,可使用 快慢指針 解決。 使用兩個指針 A、B 同時遍歷,且指針 B 始終比指針 A 快 K 個節點, 當 指針 B 遍歷到鏈表末尾時,此時 指針 A 指向的下一個節點即為倒數第 K 個節點。 【核心代碼如下:】 /** * 獲取倒數第 K 個節點。 * 方式一: * size 可知,遍歷 size - k 個節點即可 * @param k K 值,(1 ~ n,1 表示倒數第一個節點) * @return 倒數第 K 個節點 */ public Node<E> getLastKNode(int k) { Node<E> temp = header.next; // 使用臨時變量存儲第一個節點,用於輔助鏈表遍歷 // 判斷節點是否越界 if (k < 1 || k > size) { throw new IndexOutOfBoundsException("Index: " + k + ", Size: " + size); } // 遍歷 size - k 個節點,即可找到倒數第 K 個節點 for (int i = 0; i < size - k; i++) { temp = temp.next; } return temp; } /** * 獲取倒數第 K 個節點。 * 方式二: * size 未知時,使用快慢節點, * 節點 A 比節點 B 始終快 k 個節點,A,B 同時向後遍歷,當 A 遍歷完成後,B 遍歷的位置下一個位置即為倒數第 K 個節點。 * @param k K 值,(1 ~ n,1 表示倒數第一個節點) * @return 倒數第 K 個節點 */ public Node<E> getLastKNode2(int k) { Node<E> tempA = header; // 使用臨時變量存儲頭節點,用於輔助鏈表遍歷 Node<E> tempB = header; // 使用臨時變量存儲頭節點,用於輔助鏈表遍歷 // 節點越界判斷 if (k < 1) { throw new IndexOutOfBoundsException("Index: " + k); } // A 比 B 快 K 個節點 while(tempA.next != null && k != 0) { tempA = tempA.next; k--; } // 節點越界判斷 if (k != 0) { throw new IndexOutOfBoundsException("K 值大於鏈表長度"); } // 遍歷,當 A 到鏈表末尾時,B 所處位置下一個位置即為倒數第 K 個節點 while(tempA.next != null) { tempA = tempA.next; tempB = tempB.next; } return tempB.next; }
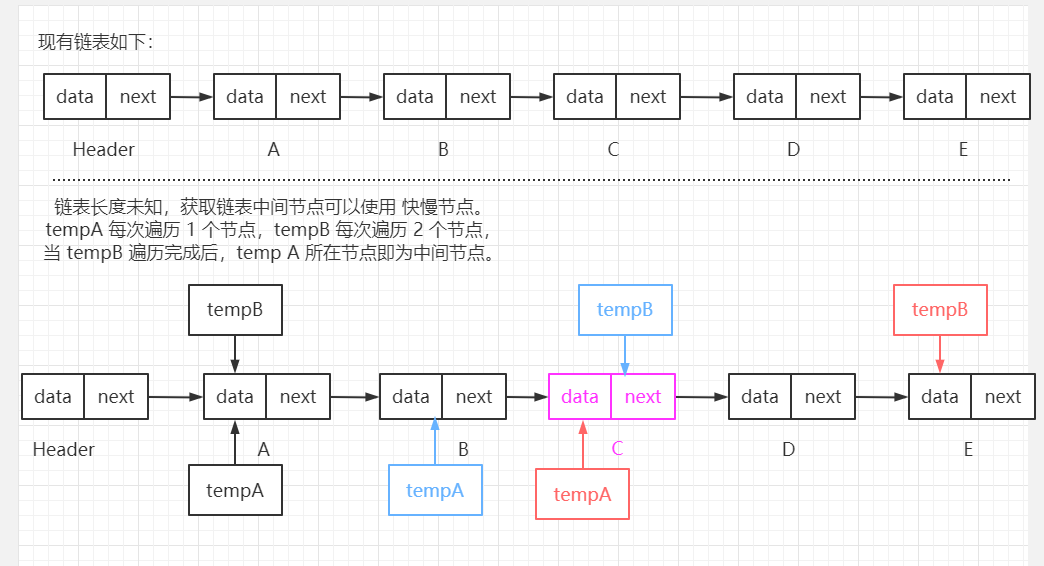
【筆試題二:】 找到當前鏈表的中間節點(鏈表長度未知)。 【筆試題二解決思路:】 鏈表長度未知,可以採用 快慢指針 方式解決。 此處與解決 上題 倒數第 K 個節點類似,只是此時節點 B 比 節點 A 每次都快 1 個節點(即 A 每次遍歷移動一個節點,B 會遍歷移動兩個節點)。 【核心代碼如下:】 /** * 鏈表長度未知時,獲取鏈表中間節點 * @return 鏈表中間節點 */ public Node<E> getHalfNode() { Node<E> tempA = header.next; // 使用臨時變量保存第一個節點,用於輔助遍歷鏈表 Node<E> tempB = header.next; // 使用臨時變量保存第一個節點,用於輔助遍歷鏈表 // 循環遍歷 B 節點,B 節點每次都比 A 節點快一個節點(每次多走一個節點),所以當 B 遍歷完成後,A 節點所處位置即為中間節點。 while(tempB.next != null && tempB.next.next != null) { tempA = tempA.next; tempB = tempB.next.next; } return tempA; }
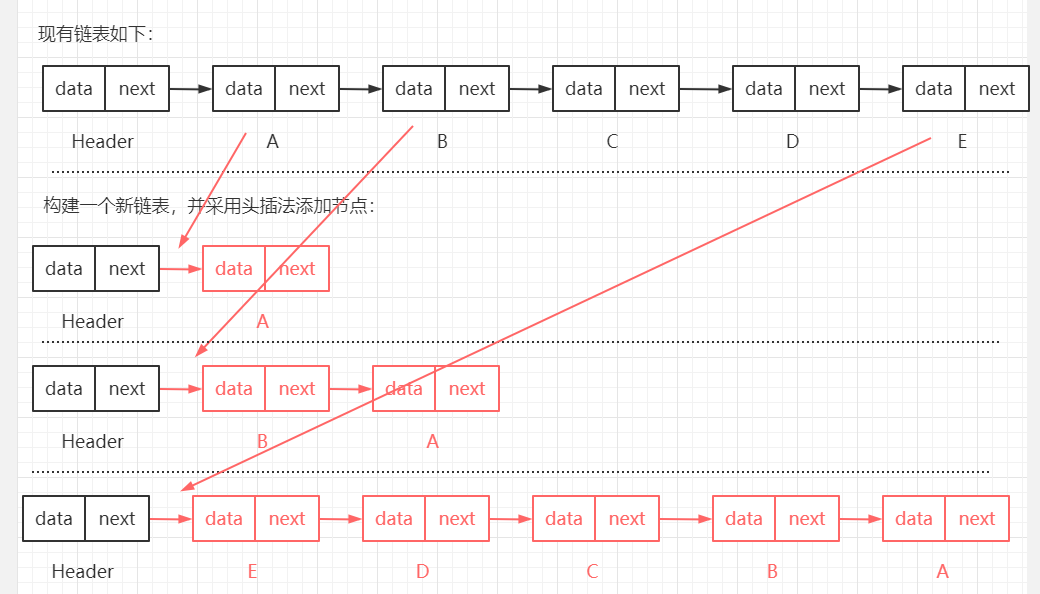
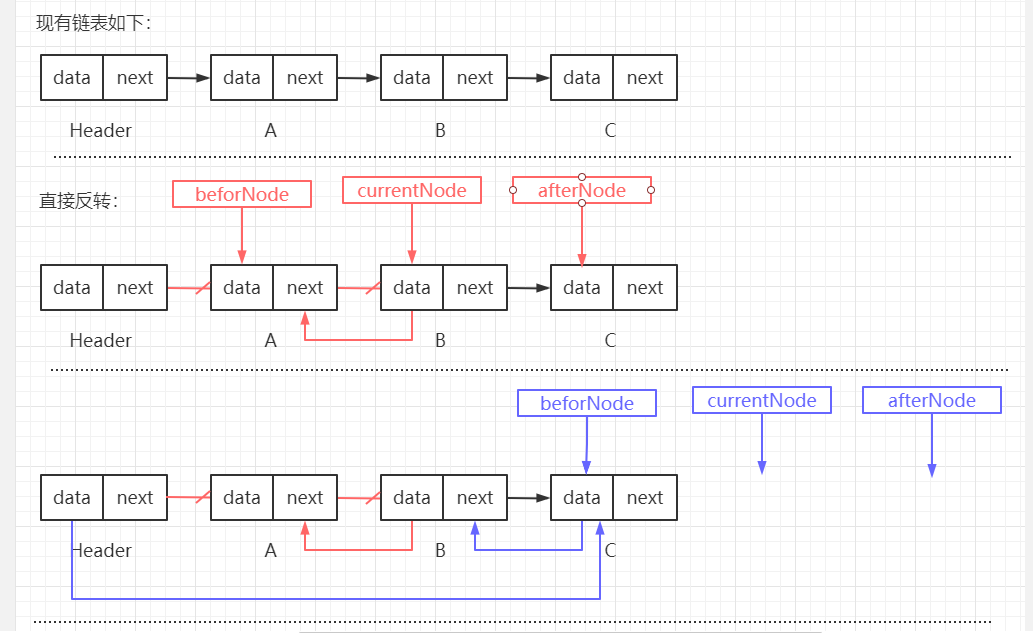
【筆試題三:】 反轉鏈表。 【筆試題三解決思路:】 思路一: 頭插法,新建一個鏈表,遍歷原始鏈表,將每個節點通過頭插法插入新鏈表。 頭插法,即每次均在第一個節點位置處進行插入操作。 思路二: 直接反轉。 通過三個指針來輔助,beforeNode、currentNode、afterNode,此時 beforeNode -> currentNode -> afterNode。 其中: beforeNode 為當前節點上一個節點。 currentNode 為當前節點。 afterNode 為當前節點下一個節點。 遍歷鏈表,使 currentNode -> beforeNode。 【核心代碼如下:】 /** * 鏈表反轉。 * 方式一: * 頭插法,新建一個鏈表,遍歷原始鏈表,將每個節點通過頭插法插入新鏈表。 * @return */ public SingleLinkedList<E> reverseList() { Node<E> temp = header.next; // 使用臨時變量存儲第一個節點,用於輔助遍歷原鏈表 SingleLinkedList singleLinkedList = new SingleLinkedList(new Node("newHeader")); // 新建一個鏈表 // 若原鏈表為空,則直接返回 空的 新鏈表 if (temp == null) { return singleLinkedList; } // 遍歷原鏈表,並調用新鏈表的 頭插法添加節點 while(temp != null) { singleLinkedList.addFirstNode(new Node(temp.data)); temp = temp.next; } return singleLinkedList; } /** * 頭插法插入節點,每次均在第一個節點位置處進行插入 * @param node 待插入節點 */ public void addFirstNode(Node<E> node) { Node<E> temp = header.next; // 使用臨時變量保存第一個節點,用於輔助遍歷鏈表 // 若鏈表為空,則直接賦值即可 if (temp == null) { header.next = node; size++; return; } // 若鏈表不為空,則在第一個節點位置進行插入 node.next = temp; header.next = node; size++; } /** * 鏈表反轉。 * 方式二: * 直接反轉,通過三個指針進行輔助。此方式會直接變化當前鏈表。 */ public void reverseList2() { // 鏈表為空直接返回 if (header.next == null) { System.out.println("當前鏈表為空"); return; } Node<E> beforeNode = null; // 指向當前節點的上個節點 Node<E> currentNode = header.next; // 指向當前節點 Node<E> afterNode = null; // 指向當前節點的下一個節點 // 遍歷節點 while(currentNode != null) { afterNode = currentNode.next; // 獲取當前節點的下一個節點 currentNode.next = beforeNode; // 將當前節點指向上一個節點 beforeNode = currentNode; // 上一個節點後移 currentNode = afterNode; // 當前節點後移,為了下一個遍歷 } header.next = beforeNode; // 遍歷結束後,beforeNode 為最後一個節點,使用 頭節點 指向該節點,即可完成鏈表反轉 }
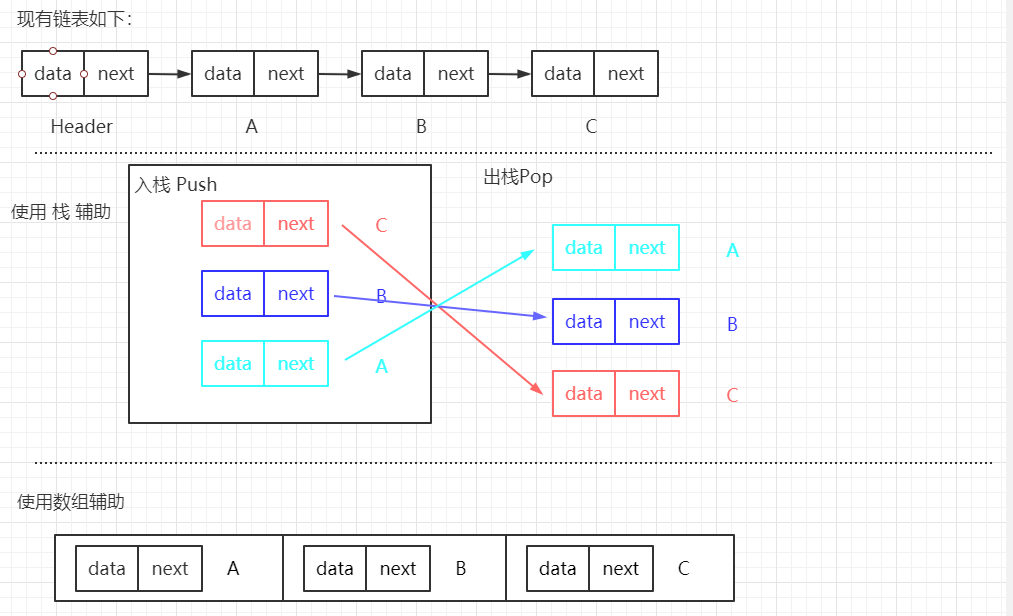
【筆試題四:】 打印輸出反轉鏈表,不能反轉原鏈表。 【筆試題四解決思路:】 思路一(此處不重複演示,詳見上例代碼): 由於不能反轉原鏈表,可以與上例頭插法相同, 新建一個鏈表並使用頭插法添加節點,最後遍歷輸出新鏈表。 思路二: 使用棧進行輔助。棧屬於先進後出結構。 可以先遍歷鏈表並存入棧中,然後依次取出棧頂元素即可。 思路三: 使用數組進行輔助(有序結構存儲一般均可,比如 TreeMap 存儲,根據 key 倒序輸出亦可)。 遍歷鏈表並存入數組,然後反序輸出數組即可(註:若是反序存入數組,可以順序輸出)。 【核心代碼如下:】 /** * 不改變當前鏈表下,反序輸出鏈表。 * 方式一: * 借用棧結構進行輔助。棧是先進後出結構。 * 先遍歷鏈表並依次存入棧,然後從棧頂挨個取出數據,即可得到反序鏈表。 */ public void printReverseList() { Node<E> temp = header.next; // 使用臨時變量保存第一個節點,用於輔助鏈表遍歷 Stack<Node<E>> stack = new Stack(); // 使用棧存儲節點 // 判斷鏈表是否為空 if (temp == null) { System.out.println("當前鏈表為空"); return; } // 遍歷節點,使用棧存儲鏈表各節點。 while(temp != null) { stack.push(temp); temp = temp.next; } // 遍歷輸出棧 while(stack.size() > 0) { System.out.print(stack.pop() + "==>"); } System.out.println(); } /** * 不改變當前鏈表下,反序輸出鏈表。 * 方式二: * 採用數組輔助。 * 遍歷鏈表存入數組,最後反序輸出數組即可(註:若是反序存入數組,可以順序輸出)。 */ public void printReverseList2() { Node<E> temp = header.next; // 使用臨時變量保存第一個節點,用於輔助鏈表遍歷 int length = size(); Node<E>[] nodes = new Node[length]; // 使用數組存儲鏈表節點 // 判斷鏈表是否為空 if(temp == null) { System.out.println("當前鏈表為空"); return; } // 遍歷鏈表,存入數組,此處反序存入數組,後面順序輸出即可 while(temp != null) { nodes[--length] = temp; temp = temp.next; } System.out.println(Arrays.toString(nodes)); }
上述所有單鏈表相關代碼完整版如下(有部分地方還需修改,僅供參考):
4、鏈表(Linked list)– 雙向鏈表、環形鏈表(約瑟夫環)
(1)雙向鏈表
通過上面單鏈表相關操作,可以知道 單鏈表的 查找方向唯一。
而雙向鏈表在 單鏈表的 基礎上在 添加一個指針域(pre),這個指針域用來指向 當前節點的上一個節點,從而實現 鏈表 雙向查找(某種程度上提高查找效率)。
【使用指針 模擬實現 雙向鏈表:】 模擬節點: 在單鏈表的基礎上,增加了一個 指向上一個節點的 指針域。 class Node2<E> { Node<E> pre; // 指針域,指向當前節點的上一個節點 Node<E> next; // 指針域,指向當前節點的下一個節點 E data; // 數據域,存儲節點數據 public Node2(E data) { this.data = data; } public Node2(E data, Node<E> pre, Node<E> next) { this.data = data; this.pre = pre; this.next = next; } } 【增刪節點:】 直接添加節點 A 到鏈表末尾: 首先得遍歷到鏈表最後一個節點 B 的位置,條件: B.next = null。 然後將 B 下一個節點指向 A, A 上一個節點指向 B。即 B.next = A; A.pre = B。 指定位置添加節點 C: 比如: A -> B 變為 A -> C -> B。 即 A.next = B; B.pre = A; 變為 C.next = B; C.pre = B.pre; B.pre.next = C; B.pre = C; 直接刪除鏈表末尾節點 A: 遍歷到鏈表最後一個節點 B 的位置,然後將其下一個節點指向 null 即可,即 B.next = null; 刪除指定位置的節點 C: 比如: A -> C -> B 變為 A -> B。 C.pre.next = C.next; C.next.pre = C.pre;


(2)雙向鏈表代碼實現如下:
【代碼實現:】 package com.lyh.com.lyh.linkedlist; public class DoubleLinkedList<E> { private int size = 0; // 用於保存鏈表實際長度 private Node2<E> header; // 用於保存鏈表頭節點,僅用作 起點,不存儲數據。 public DoubleLinkedList(Node2<E> header) { this.header = header; } /** * 直接在鏈表末尾添加節點 * @param node 待添加節點 */ public void addLastNode(Node2<E> node) { Node2<E> temp = header; // 使用臨時變量保存頭節點,用於輔助鏈表遍歷 // 遍歷鏈表至鏈表末尾 while(temp.next != null) { temp = temp.next; } // 添加節點 temp.next = node; node.pre = temp; size++; } /** * 直接在鏈表末尾添加節點 * @param data 待添加數據 */ public void addLastNode2(E data) { Node2<E> temp = header; // 使用臨時節點保存頭節點,用於輔助鏈表遍歷 Node2<E> newNode = new Node2<>(data); // 創建新節點 // 遍歷鏈表至鏈表末尾 while(temp.next != null) { temp = temp.next; } // 添加節點 temp.next = newNode; newNode.pre = temp; size++; } /** * 遍歷輸出鏈表 */ public void showList() { Node2<E> temp = header.next; // 使用臨時變量保存第一個節點,用於輔助遍歷鏈表 // 判斷鏈表是否為空 if(temp == null) { System.out.println("當前鏈表為空"); return; } // 遍歷輸出鏈表 System.out.print("當前鏈表長度為: " + size() + " == 當前鏈表為: "); while(temp != null) { System.out.print(temp + " ==> "); temp = temp.next; } System.out.println(); } /** * 返回鏈表長度 * @return 鏈表長度 */ public int size() { return this.size; } /** * 在指定位置添加節點 * @param index 1 ~ n(1 表示 第一個節點) */ public void insert(int index, Node2<E> newNode) { Node2<E> temp = header; // 使用臨時變量保存頭節點,用於輔助鏈表遍歷 // 遍歷找到指定位置 while(index != 0 && temp.next != null) { temp = temp.next; index--; } if (index != 0) { throw new IndexOutOfBoundsException("指定位置有誤: " + index); } newNode.next = temp; newNode.pre = temp.pre; temp.pre.next = newNode; temp.pre = newNode; size++; } /** * 刪除指定位置的節點 * @param index 1 ~ n(1 表示第一個節點) */ public void delete(int index) { Node2<E> temp = header; // 使用臨時變量保存頭節點,用於輔助鏈表遍歷 // 遍歷找到待刪除節點位置 while(index != 0 && temp.next != null) { index--; temp = temp.next; } // 判斷節點是否存在 if (index != 0) { throw new IndexOutOfBoundsException("指定節點位置不存在"); } temp.pre.next = temp.next; // 若節點為最後一個節點,則無需對下一個節點進行賦值操作 if (temp.next != null) { temp.next.pre = temp.pre; } size--; } /** * 直接刪除鏈表末尾節點 */ public void deleteLastNode() { Node2<E> temp = header; // 使用臨時變量保存頭節點,用於輔助鏈表遍歷 // 判斷鏈表是否為空 if (temp.next == null) { System.out.println("當前鏈表為空"); return; } // 遍歷鏈表至最後一個節點 while(temp.next != null) { temp = temp.next; } temp.pre.next = null; size--; } public static void main(String[] args) { // 創建雙向鏈表 DoubleLinkedList<String> doubleLinkedList = new DoubleLinkedList<>(new Node2<>("header")); // 輸出鏈表 doubleLinkedList.showList(); System.out.println("=========================="); // 添加節點 doubleLinkedList.addLastNode(new Node2<>("Java")); doubleLinkedList.addLastNode2("JavaScript"); doubleLinkedList.insert(2, new Node2<>("E")); doubleLinkedList.insert(1, new Node2<>("F")); // 輸出鏈表 doubleLinkedList.showList(); System.out.println("=========================="); doubleLinkedList.delete(1); doubleLinkedList.deleteLastNode(); // 輸出鏈表 doubleLinkedList.showList(); System.out.println("=========================="); } } class Node2<E> { Node2<E> pre; // 指針域,指向當前節點的上一個節點 Node2<E> next; // 指針域,指向當前節點的下一個節點 E data; // 數據域,存儲節點數據 public Node2(E data) { this.data = data; } public Node2(E data, Node2<E> pre, Node2<E> next) { this.data = data; this.pre = pre; this.next = next; } @Override public String toString() { return "Node2{ pre= " + (pre != null ? pre.data : null) + ", next= " + (next != null ? next.data : null) + ", data= " + data + '}'; } } 【輸出結果:】 當前鏈表為空 ========================== 當前鏈表長度為: 4 == 當前鏈表為: Node2{ pre= header, next= Java, data= F} ==> Node2{ pre= F, next= E, data= Java} ==> Node2{ pre= Java, next= JavaScript, data= E} ==> Node2{ pre= E, next= null, data= JavaScript} ==> ========================== 當前鏈表長度為: 2 == 當前鏈表為: Node2{ pre= header, next= E, data= Java} ==> Node2{ pre= Java, next= null, data= E} ==> ==========================
(3)單向環形鏈表
單向循環鏈表 指的是 在單鏈表基礎上,將 最後一個節點的指針域 指向第一個節點,從而使鏈表變成一個環狀結構。
其最常見的應用場景就是 約瑟夫環 問題。
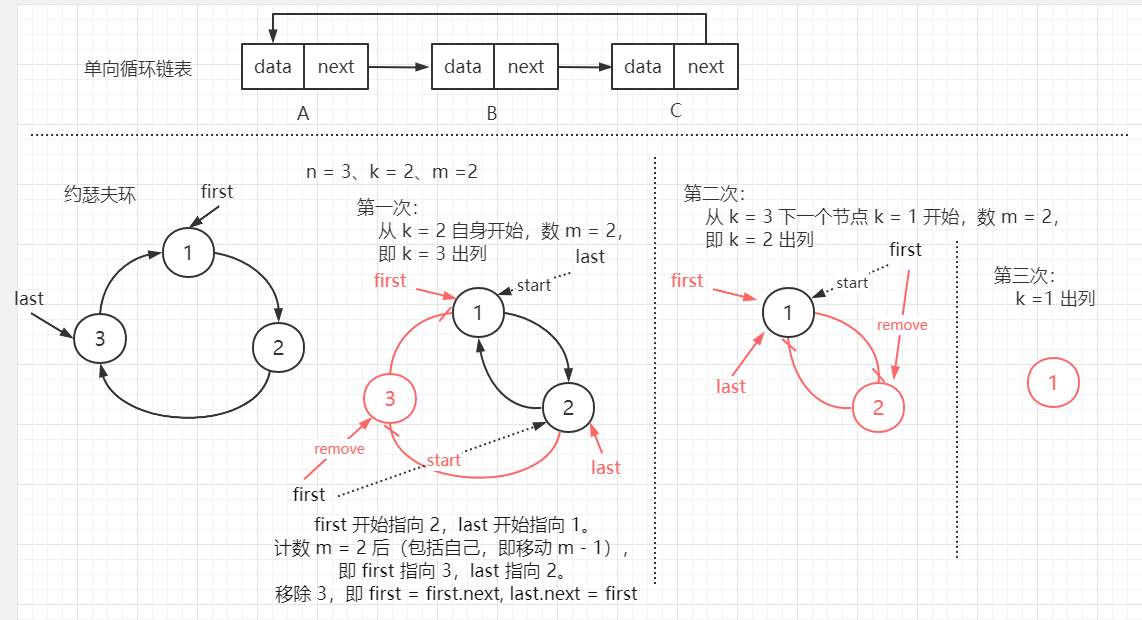
【約瑟夫(josephu)環問題:】 已知 n 個人圍成一圈,編號由 1 ~ n,從編號為 k (1 <= k <= n)的人開始從 1 報數,數到 m 的那個人出列。 並從下一個人開始重新報數,再次數到 m 的人出列,依次類推,直至所有人出列,問 n 個人的出隊編號(或者最後一個出隊的是誰)。 【解決思路:】 使用一個不帶頭節點的單向循環鏈表處理。 先構成一個有 n 個節點的單向循環鏈表(構建一個單鏈表,並另最後一個節點 last 指向 第一個節點,即 last.next = first), 由 k 節點開始從 1 計數,移動 m 個節點後將對應的節點從鏈表中刪除。並從下一個節點開始計數,直至最後一個節點。 使用 兩個節點指針來輔助鏈表遍歷 -- first(指向當前第一個節點、且用於表示待移除的節點)、last(指向當前最後一個節點)。 先遍歷到 k 點(即 first 指向 k 點,last 指向 k 點上一個節點),計數(包括自身,所以 first、last 移動 m - 1 個節點), 此時 first 指向的即為待輸出的節點,輸出後,將其移除。即 first = first.next; last.next = first; 同理,從移除節點的下一個節點開始操作,當鏈表只剩最後一個節點,即 first == last 時,遍歷結束,輸出最後一個節點 即可。 註: last.next == first 表示環滿 last == first 表示環空,即環里只有一個節點 【代碼實現:】 package com.lyh.com.lyh.linkedlist; public class CircleSingleLinkedList<E> { private Node3<E> first; // 保存第一個節點 /** * 構成單向環形鏈表 * @param num 鏈表節點個數 (1 ~ n, 1 表示 1 個節點) */ public void addNode(int num) { // 判斷 num 是否合適 if (num < 1) { throw new IndexOutOfBoundsException("數據不能構成環"); } Node3 temp = null; // 輔助指針,用於記錄尾節點 // 添加節點,構成循環鏈表 for (int i = 1; i <= num; i++) { Node3 node = new Node3(i); // 構建新節點 if (i == 1) { // 只有一個節點時,即為首節點 first = node; temp = first; } else { // 添加尾節點 temp.next = node; temp = node; } } // 尾節點指向首節點,構成環 temp.next = first; } /** * 遍歷輸出當前環形鏈表 */ public void showList() { Node3<E> temp = first; // 使用臨時變量存儲第一個節點,用於輔助鏈表遍歷 if (temp == null) { System.out.println("當前鏈表為空"); return; } System.out.print("當前鏈表為: "); while(temp.next != first) { System.out.print(temp + " ==> "); temp = temp.next; } System.out.println(temp); } /** * 按要求輸出 移除節點 順序 * @param num 節點總數(n) * @param start 開始節點編號(1 ~ n) * @param count 計數(1 ~ m) */ public void printList(int num, int start, int count) { Node3<E> last = first; // 用於記錄當前鏈表最後一個節點 if (last == null || start < 1 || start > num) { throw new RuntimeException("參數不合法"); } // 遍歷,得到最後一個節點 while(last.next != first) { last = last.next; } // 找到開始節點, first 表示開始節點,last 表示最後一個節點(即開始節點的上一個節點) while(start != 1) { last = last.next; first = first.next; start--; } // 遍歷輸出節點(開始節點、最後節點重合時 即鏈表只存在一個節點) while(last != first) { // 找到待移除節點,由於當前節點會被計算,所以只需移動 count - 1 個節點。 for (int i = 1; i < count; i++) { first = first.next; last = last.next; } System.out.print(first + " ==> "); // 移除節點(first 為被移除節點, 即 last -> first -> A 變為 fisrt = A 且 last -> A) first = first.next; last.next = first; } System.out.println(last); } public static void main(String[] args) { // 構建一個空的循環鏈表 CircleSingleLinkedList<Integer> circleSingleLinkedList = new CircleSingleLinkedList<>(); circleSingleLinkedList.showList(); System.out.println("========================"); // 添加節點 int num = 5; // 節點個數 circleSingleLinkedList.addNode(num); circleSingleLinkedList.showList(); System.out.println("========================"); // 輸出節點 出鏈表順序 int start = 2; // 開始編號 K int count = 2; // 計數 circleSingleLinkedList.printList(num, start, count); } } class Node3<E> { Node3<E> next; // 指針域,存儲下一個節點 E data; // 數據域,存儲節點數據 public Node3(E data) { this.data = data; } public Node3(Node3<E> next, E data) { this.next = next; this.data = data; } @Override public String toString() { return "Node3{ data= " + data + '}'; } } 【輸出結果:】 當前鏈表為空 ======================== 當前鏈表為: Node3{ data= 1} ==> Node3{ data= 2} ==> Node3{ data= 3} ==> Node3{ data= 4} ==> Node3{ data= 5} ======================== Node3{ data= 3} ==> Node3{ data= 5} ==> Node3{ data= 2} ==> Node3{ data= 1} ==> Node3{ data= 4}
5、棧(Stack)
(1)什麼是棧?
棧指的是一種 受限、線性的數據結構,其僅允許在 一端 進行插入(棧頂插入 push)、刪除操作(棧頂刪除 pop)。其允許插入、刪除的一端為 棧頂(Top),另一端為棧底(Bottom)。
棧可以使用 數組 或者 鏈表 實現(一般採用數組實現,僅在首或尾增刪,效率比鏈表高)。其遵循 先進後出(First In Last Out,FILO) 原則,即先存入 棧的值 後取出。

(2)常用場景:
二叉樹遍歷(迭代法)。
圖的深度優先搜索法。
表達式轉換與求值(比如:中綴表達式 轉 後綴表達式)。
堆棧,比如:JVM 虛擬機棧 處理遞歸、子程序調用時,存儲下一個指令地址 或者 參數、變量。
(3)使用數組模擬棧操作
【使用數組模擬棧操作:】 定義 top 用於記錄當前棧頂指向,初始值為 -1。 數據 data 進棧時,top 先加 1 再賦值,即 stack[++top] = data。 數據 data 出棧時,先保存出棧的值,top 再減 1,即 data = stack[top--] 【代碼實現:】 package com.lyh.stack; public class ArrayStack { private int maxSize; // 記錄棧的大小(最大容量) private String[] stack; // 用於記錄 private int top = -1; // 用於初始化棧頂位置 public ArrayStack(int maxSize) { this.maxSize = maxSize; this.stack = new String[maxSize]; } /** * 判斷棧是否為空 * @return true 為空 */ public boolean isEmpty() { return top == -1; } /** * 判斷棧是否已滿 * @return true 表示已滿 */ public boolean isFull() { return top == maxSize - 1; } /** * 數據入棧 * @param data 待入棧數據 */ public void push(String data) { // 判斷棧是夠已滿,已滿則不能再添加數據 if (isFull()) { System.out.println("棧滿,無法添加"); return; } // top 加 1,並存值 this.stack[++top] = data; } /** * 數據出棧 * @return 出棧數據 */ public String pop() { // 判斷棧是否為空,為空則無法返回數據 if(isEmpty()) { System.out.println("棧空,無數據"); return null; } // 取值,top 減 1 return this.stack[top--]; } /** * 遍歷輸出棧元素 */ public void showList() { // 判斷棧是否為空 if (isEmpty()) { System.out.println("棧空"); return; } System.out.print("當前棧存儲數據個數為: " + (top + 1) + " 當前棧輸出為: "); for(int i = top; i >= 0; i--) { System.out.print(this.stack[i] + " == "); } System.out.println(); } public static void main(String[] args) { // 實例化棧 ArrayStack arrayStack = new ArrayStack(10); // 遍歷棧 arrayStack.showList(); System.out.println("========================"); // 數據入棧 arrayStack.push("Java"); arrayStack.push("Python"); arrayStack.push("JavaScript"); // 遍歷棧 arrayStack.showList(); System.out.println("========================"); // 數據出棧 System.out.println(arrayStack.pop()); System.out.println("========================"); // 遍歷棧 arrayStack.showList(); System.out.println("========================"); } } 【輸出結果:】 棧空 ======================== 當前棧存儲數據個數為: 3 當前棧輸出為: JavaScript == Python == Java == ======================== JavaScript ======================== 當前棧存儲數據個數為: 2 當前棧輸出為: Python == Java == ========================
6、使用棧計算 前綴(波蘭)、中綴、逆波蘭(後綴)表達式
(1)表達式的三種表示形式:
表達式可以分為三種表示形式:
前綴(波蘭)表達式。其運算符在操作數之前。
中綴表達式。常見的算術公式(運算符在操作數中間),其括號不可省。
後綴(逆波蘭)表達式。其運算符在操作數之後。
舉例(以下為表達式的三種表示形式):
前綴表達式:+ 3 4
中綴表達式:3 + 4
後綴表達式:4 3 +
註:
中綴表達式雖然易讀,但是計算機處理起來稍微有點麻煩(比如:括號的處理),不如 前綴、後綴 處理方便(消除了括號)。
所以一般處理表達式時 會對表達式進行轉換,比如:中綴表達式轉為後綴表達式,然後再對 後綴表達式進行處理。
中綴轉後綴、中綴轉前綴 過程類似,需要注意的是(詳細可見下面轉換步驟):
中綴轉前綴時,從右至左掃描字符串,且遇到右括號 “)” 直接入棧。
中綴轉後綴時,從左至右掃描字符串,且遇到左括號 “(” 直接入棧。
(2)前綴表達式 以及 中綴 轉 前綴
【前綴(波蘭)表達式:】 基本概念: 前綴表達式又稱為 波蘭表達式,其運算符(+、-、*、/)位於操作數前。 舉例: 一個表達式為:(3 + 4) * 5 - 6,其 對應的前綴表達式為 - * + 3 4 5 6。 如何處理前綴表達式: Step1:需要一個棧來存儲操作數,從右至左掃描表達式。 Step1.1:如果掃描的是數字,那麼就將數字入棧, Step1.2:如果掃描的是字符(+、-、*、/),就彈出棧頂值兩次,並通過運算符進行計算,最後將結果再次入棧。 Step2:重複 Step1 過程直至 表達式掃描完成,最後棧中的值即為 表達式結果。 如何處理前綴表達式(- * + 3 4 5 6): Step1:從右至左掃描,依次將 6 5 4 3 入棧。此時棧元素為 6 5 4 3。 Step1.1:掃描到 +,彈出棧頂值 3、4,相加(4 + 3 = 7)併入棧,即 此時棧元素為 6 5 7。 Step1.2:掃描到 *,彈出棧頂值 7、5,相乘(5 * 7 = 35)併入棧,即 此時棧元素為 6 35。 Step1.3:掃描到 -,彈出棧頂值 6、35,相減(35 - 6 = 29)併入棧,即 此時棧元素為 29。 【中綴表達式 轉換為 前綴表達式:】 中綴表達式轉前綴表達式步驟: Step1:初始化兩個棧 A、B,A 用於記錄 運算符、B 用於記錄 中間結果。 Step2:從右至左掃描 中綴表達式。 Step2.1:如果掃描的是數字,直接將其壓入棧 B。 Step2.2:如果掃描的是運算符(+、-、*、/),則比較當前運算符 與 A 棧頂運算符 的優先級。 Step2.2.1:若 A 為空 或者 棧頂運算符為右括號 ")",則當前運算符 直接入棧。 Step2.2.2:若上麵條件不滿足,則比較優先級,若當前運算符優先級 比 A 棧頂運算符 優先級高,則當前運算符 也入棧。 Step2.2.3:若上麵條件不滿足,即當前運算符優先級低,則將 A 棧頂運算符彈出並壓入 B 棧。重新執行 Step2.2 進行運算符比較。 Step2.3:如果掃描的是括號 Step2.3.1:如果為右括號 ")",則直接壓入 A 棧。 Step2.3.2:如果為左括號 "(",則依次彈出 A 棧頂元素並壓入 B 棧,直至遇到 右括號 ")",此時 這對括號可以 捨棄。 Step2.4:重複上面掃描步驟,直至表達式掃描完成。 Step3:將 A 棧中剩餘元素依次取出並壓入 B 棧。 Step4:此時 B 棧順序取出結果即為前綴表達式。 中綴表達式 "(3 + 4) * 5 - 6" 如何 轉為前綴表達式 "- * + 3 4 5 6": Step1:初始化兩個棧 A、B。A 存儲運算符,B 存儲中間結果。從右到左掃描中綴表達式。 Step1.1:掃描到 6,直接存入 B 棧,此時 A 棧元素為 空,B 棧元素為 6。 Step1.2:掃描到 -,此時 A 棧為空,直接存入 A 棧,此時 A 棧元素為 -,B 棧元素為 6。 Step1.3:掃描到 5,直接存入 B 棧,此時 A 棧元素為 -,B 棧元素為 6 5。 Step1.4:掃描到 *,當前運算符 * 比 A 棧頂運算符 優先級高,直接入棧,即此時 A 棧元素為 - *,B 棧元素為 6 5。 Step1.5:掃描到 ),直接入 A 棧,此時 A 棧元素為 - * ),B 棧元素為 6 5。 Step1.6:掃描到 4,直接存入 B 棧,此時 A 棧元素為 - * ),B 棧元素為 6 5 4。 Step1.7:掃描到 +,由於棧頂元素為右括號 ")",直接入 A 棧,此時 A 棧元素為 - * ) +,B 棧元素為 6 5 4。 Step1.8:掃描到 3,直接入 B 棧,此時 A 棧元素為 - * ) +,B 棧元素為 6 5 4 3。 Step1.9:掃描到左括號 "(",A 棧頂元素出棧並壓入 B 棧直至遇到 右括號 ")",且移除括號,此時 A 棧元素為 - *, B 棧元素為 6 5 4 3 +。 Step2:將 A 棧剩餘元素依次取出並壓入 B 棧。此時 A 棧為空,B 棧元素為 6 5 4 3 + * -。 Step3:將 B 依次取出即為前綴表達式 "- * + 3 4 5 6"。
(3)中綴表達式
【中綴表達式:】 基本概念: 中綴表達式就是最常見的運算表達式,其運算符在操作數中間。 註: 中綴表達式括號不可省,其用於表示運算的優先順序。 舉例: 一個表達式為:(3 + 4) * 5 - 6,這就是中綴表達式。 如何處理中綴表達式: Step1:需要兩個棧 A、B,A 用於存放 操作數,B 用於存放 符號(運算符、括號)。 Step2:從左到右掃描 中綴表達式。 Step2.1:如果掃描的是 數字,則直接壓入 A 棧。 Step2.2:如果掃描的是 運算符(+、-、*、/),則比較當前運算符 與 B 棧頂運算符 的優先級。 Step2.2.1:若 B 為空 或者 棧頂元素為左括號 "(",則當前運算符直接入棧。 Step2.2.2:若上麵條件不滿足,則比較優先級,若當前運算符 比 B 棧頂運算符 優先級高,則當前運算符 入 B 棧。 Step2.2.3:若上麵條件不滿足,即當前運算符優先級低,則將 B 棧頂運算符彈出,並彈出 A 棧頂兩個數據進行 計算,最後將計算結果存入 A 棧。重新執行 Step2.2 進行運算符比較。 Step2.3:如果掃描的是括號: Step2.3.1:若為左括號 "(",則直接壓入 B 棧。 Step2.3.2:若為右括號 ")",則依次彈出 B 棧運算符直至遇到左括號 "(",B 棧每取一個元素,A 棧取兩個元素,計算後將結果重新壓入 A 棧。 Step2.4:重複上面掃描步驟,直至表達式掃描完成。 Step3:依次取出 B 棧頂運算符 以及 A 棧頂元素 計算,最後結果即為 表達式結果。 註: 直接處理中綴表達式,在於其會直接通過 運算符 進行運算。 如何處理中綴表達式 "(3 + 4) * 5 - 6": Step1:初始化兩個棧 A、B。A 用於記錄 操作數, B 用於記錄 運算符。 Step2:從左至右掃描 中綴表達式。 Step2.1:掃描到左括號 "(",直接入 B 棧,此時 A 棧元素為空,B 棧元素為 (。 Step2.2:掃描到 3,直接入 A 棧,此時 A 棧元素為 3,B 棧元素為 (。 Step2.3:掃描到 +,此時 B 棧頂元素為左括號 "(",直接入 B 棧,此時 A 棧元素為 3,B 棧元素為 ( +。 Step2.4:掃描到 4,直接入 A 棧,此時 A 棧元素為 4,B 棧元素為 ( +。 Step2.5:掃描到右括號 ")",B 棧頂元素 + 出棧,A 棧彈出 4、 3,計算後重新壓入 A 棧, B 繼續彈出棧頂元素為左括號 "(",直接將其出棧。此時 A 棧元素為 7,B 棧元素為空。 Step2.6:掃描到 *,B 棧元素為空,直接入 B 棧,此時 A 棧元素為 7,B 棧元素為 *。 Step2.7:掃描到 5,直接入 A 棧,此時 A 棧元素為 7 5,B 棧元素為 *。 Step2.8:掃描到 -,當前運算符 - 比 B 棧頂運算符優先級 低,B 棧頂運算符出棧,A 棧彈出 5、7,計算後壓入 A 棧, 此時 B 棧為空,當前運算符直接壓入 B 棧,即此時 A 棧元素為 35,B 棧元素為 -。 Step2.9:掃描到 6,直接入 A 棧,此時 A 棧元素為 35 6, B 棧元素為 -。 Step3:取出 B 棧頂元素 -,A 棧彈出元素 6、35,計算後壓入 A 棧,此時 B 棧為空,即表達式計算結束,A 棧最終結果即為表達式結果,即 29。
(4)後綴表達式 以及 中綴 轉 後綴
【後綴(逆波蘭)表達式:】 基本概念: 後綴表達式又稱為 逆波蘭表達式,其運算符位於操作數之後。 舉例: 一個表達式為:(3 + 4) * 5 - 6,其 對應的前綴表達式為:3 4 + 5 * 6 - 如何處理後綴表達式: Step1:需要一個棧來存儲操作數,從左至右掃描表達式。 Step1.1:如果掃描的是數字,那麼就將數字入棧, Step1.2:如果掃描的是字符(+、-、*、/),就彈出棧頂值兩次,並通過運算符進行計算,最後將結果再次入棧。 Step2:重複 Step1 過程直至 表達式掃描完成,最後棧中的值即為 表達式結果。 如何處理後綴表達式(3 4 + 5 * 6 -): Step1:從左至右掃描,依次將 3 4 入棧。此時棧元素為 3 4。 Step1.1:掃描到 +,彈出棧頂值 3、4,相加併入棧,即 此時棧元素為 7。 Step1.2:掃描到 5,入棧,即 此時棧元素為 7 5。 Step1.3:掃描到 *,彈出棧頂值 5、7,相乘併入棧,即 此時棧元素為 35。 Step1.4:掃描到 6,入棧,即 此時棧元素為 35 6。 Step1.5:掃描到 -,彈出棧頂值 6、35,相減併入棧,即 此時棧元素為 29。 【中綴表達式 轉換為 後綴表達式:】 中綴表達式轉後綴表達式步驟: Step1:初始化兩個棧 A、B,A 用於記錄 運算符、B 用於記錄 中間結果。 Step2:從左至右掃描 中綴表達式。 Step2.1:如果掃描的是數字,直接將其壓入棧 B。 Step2.2:如果掃描的是運算符(+、-、*、/),則比較當前運算符 與 A 棧頂運算符 的優先級。 Step2.2.1:若 A 為空 或者 棧頂運算符為左括號 "(",則當前運算符 直接入棧。 Step2.2.2:若上麵條件不滿足,則比較優先級,若當前運算符優先級 比 A 棧頂運算符 優先級高,則當前運算符 也入棧。 Step2.2.3:若上麵條件不滿足,即當前運算符優先級低,則將 A 棧頂運算符彈出並壓入 B 棧。重新執行 Step2.2 進行運算符比較。 Step2.3:如果掃描的是括號 Step2.3.1:如果為左括號 "(",則直接壓入 A 棧。 Step2.3.2:如果為右括號 ")",則依次彈出 A 棧頂元素並壓入 B 棧,直至遇到 左括號 "(",此時 這對括號可以 捨棄。 Step2.4:重複上面掃描步驟,直至表達式掃描完成。 Step3:將 A 棧中剩餘元素依次取出並壓入 B 棧。 Step4:此時 B 棧逆序結果即為後綴表達式。 註: 實際寫代碼時,由於 B 棧自始至終不會進行彈出操作,且其結果的 逆序 才是 後綴表達式。 所以為了減少一次 逆序 的過程,可以直接使用 數組 或者 鏈表 進行存儲,然後 順序讀取即可。 中綴表達式 "(3 + 4) * 5 - 6" 如何 轉為後綴表達式 "3 4 + 5 * 6 -": Step1:初始化兩個棧 A、B。A 存儲運算符,B 存儲中間結果。從左至右掃描中綴表達式。 Step1.1:掃描到左括號 "(",壓入 A 棧,此時 A 棧元素為 (,B 棧元素為空。 Step1.2:掃描到 3,壓入 B 棧,此時 A 棧元素為 (,B 棧元素為 3。 Step1.3:掃描到 +,由於 A 棧頂元素為左括號 "(",所以直接入棧。此時 A 棧元素為 ( +,B 棧元素為 3。 Step1.4:掃描到 4,壓入 B 棧,此時 A 棧元素為 ( +,B 棧元素為 3 4。 Step1.5:掃描到右括號 ),A 棧元素依次出棧壓入 B 直至遇到左括號 "(",並移除括號。此時 A 棧元素為 空,B 棧元素為 3 4 +。 Step1.6:掃描到 *,由於 A 棧為空直接入棧,此時 A 棧元素為 *,B 棧元素為 3 4 +。 Step1.7:掃描到 5,壓入 B 棧,A 棧元素為 *,B 棧元素為 3 4 + 5。 Step1.8:掃描到 -,當前運算符 - 優先級低於 A 優先級,所以 A 棧頂元素彈出並壓入 B 棧,此時 A 棧為空,當前運算符直接存入。此時 A 棧元素為 -,B 棧元素為 3 4 + 5 *。 Step1.9:掃描到 6,壓入 B 棧,此時 A 棧元素為 -,B 棧元素為 3 4 + 5 * 6。 Step2:將 A 剩餘元素出棧並壓入 B。此時 A 棧為空,B 棧元素為 3 4 + 5 * 6 -。 Step3:將 B 棧元素依次取出並倒序輸出,即為 後綴表達式 "3 4 + 5 * 6 -"。
(5)中綴表達式、前綴表達式、後綴表達式代碼實現
如下代碼,實現 基本表達式(多位數且帶括號)的 +、-、*、/。
此處直接使用 Stack 類作為 棧 使用,不使用自定義棧結構。
【代碼實現:】 package com.lyh.stack; import java.util.ArrayList; import java.util.List; import java.util.Stack; public class Expression { public static void main(String[] args) { Expression expressionDemo = new Expression(); // 定義一個表達式(默認格式正確,此處不做過多的格式校驗) // String expression = ("2+3*(7-4)+8/4").trim(); String expression = ("(13-6)*5-6").trim(); System.out.println("當前表達式為: " + expression); System.out.println("================================"); List<String> infixExpressionList = expressionDemo.transfor(expression); System.out.println("表達式轉換後為中綴表達式: " + infixExpressionList); System.out.println("================================"); System.out.println("中綴表達式求值為: " + expressionDemo.infixExpression(infixExpressionList)); System.out.println("================================"); List<String> prefixExpressionList = expressionDemo.infixToPrefix(infixExpressionList); System.out.println("中綴表達式: " + infixExpressionList + " 轉為 前綴表達式: " + prefixExpressionList); System.out.println("前綴表達式求值為: " + expressionDemo.prefixExpression(prefixExpressionList)); System.out.println("================================"); List<String> suffixExpressionList = expressionDemo.infixToSuffix(infixExpressionList); System.out.println("中綴表達式: " + infixExpressionList + " 轉為 後綴表達式: " + suffixExpressionList); System.out.println("後綴表達式求值為: " + expressionDemo.suffixExpression(suffixExpressionList)); System.out.println("================================"); } /** * 字符串轉換成集合保存,便於操作 * @param expression 待轉換的表達式 * @return 轉換完成的表達式 */ public List<String> transfor(String expression) { // 用於保存最終結果 List<String> result = new ArrayList<>(); // 用於轉換多位數 String temp = ""; // 遍歷字符串,將其 數據取出(可能存在多位數) 挨個存入集合 for(int i = 0; i < expression.length(); i++) { // 遇到多位數,就使用 temp 拼接 while(i < expression.length() && expression.charAt(i) >= '0' && expression.charAt(i) <= '9') { temp += expression.charAt(i); i++; } // 將多位數存放到集合中 if (temp != "") { result.add(temp); temp = ""; } // 存放符號(+、-、*、/、括號) if (i < expression.length()) { result.add(String.valueOf(expression.charAt(i))); } } return result; } /** * 中綴表達式求值(從左到右掃描表達式) * @param expression 表達式 * @return 計算結果 */ public String infixExpression(List<String> expression) { Stack<String> stackA = new Stack<>(); // 用於存放操作數,簡稱 A 棧 Stack<String> stackB = new Stack<>(); // 用於存放運算符,簡稱 B 棧 // 遍歷集合,取出表達式中 數據 以及 運算符 存入棧中並計算 expression.forEach(x -> { // 如果取出的是數據,直接存放進 A 棧 if (x.matches("\\d+")) { stackA.push(x); } else { // 如果當前運算符為右括號 ")" if (")".equals(x)) { // 依次取出 B 棧頂運算符 以及 A 棧頂兩個元素進行計算,計算結果再存入 A 棧,直至遇到左括號 "(" while(stackB.size() > 0 && !"(".equals(stackB.peek())) { stackA.push(calculate(stackA.pop(), stackA.pop(), stackB.pop())); } // 移除左括號 "(" 與 當前運算符右括號 ")",即此次比較結束。 stackB.pop(); } else { // 比較運算符優先級,判斷當前運算符是直接進入 B 棧,還是先取出優先級高的運算符計算後、再將當前運算符入棧。 while(true) { // 如果 當前運算符為左括號 "(" 或者 B 棧為空 或者 B 棧頂元素為 左括號 "(" 或者 當前運算符優先級 高於 B 棧頂元素優先級,則當前運算符直接入棧 if ("(".equals(x) || stackB.size() == 0 || "(".equals(stackB.peek()) || priority(x) > priority(stackB.peek())) { stackB.push(x); break; } // 以上條件均不滿足,即當前運算符優先級 小於等於 B 棧頂元素優先級 // if (priority(x) <= priority(stackB.peek())) { // 依次取出 B 棧頂運算符 以及 A 棧頂兩個元素進行計算,計算結果再存入 A 棧 stackA.push(calculate(stackA.pop(), stackA.pop(), stackB.pop())); // } } } } }); // 依次取出 B 棧頂運算符 以及 A 棧頂兩個元素進行計算,計算結果再存入 A 棧 while(stackB.size() > 0) { stackA.push(calculate(stackA.pop(), stackA.pop(), stackB.pop())); } return stackA.pop(); } /** * 返回運算符優先級 * @param operator 運算符 * @return 優先級(0 ~ n, 0 為最小優先級) */ public int priority(String operator) { switch (operator) { case "+": return 1; case "-": return 1; case "*": return 2; case "/": return 2; default: return 0; } } /** * 根據運算符 計算 兩數據,並返回計算結果 * @param num 數據 A * @param num2 數據 B * @param operator 運算符 * @return 計算結果 */ public String calculate(String num, String num2, String operator) { String result = ""; switch (operator) { case "+": result = String.valueOf(Integer.valueOf(num2) + Integer.valueOf(num)); break; case "-": result = String.valueOf(Integer.valueOf(num2) - Integer.valueOf(num)); break; case "*": result = String.valueOf(Integer.valueOf(num2) * Integer.valueOf(num)); break; case "/": result = String.valueOf(Integer.valueOf(num2) / Integer.valueOf(num)); break; default: result = ""; break; } return result; } /** * 前綴表達式求值(從右到左掃描表達式) * @param expression 前綴表達式 * @return 計算結果 */ public String prefixExpression(List<String> expression) { Stack<String> stackA = new Stack<>(); // 用於存儲操作數,簡稱 A 棧 // 從右到左掃描表達式 for (int i = expression.size() - 1; i >= 0; i--) { // 用於保存當前表達式數據(操作數 或者 運算符) String temp = expression.get(i); // 如果當前數據為 操作數,則直接存入 A 棧 if (temp.matches("\\d+")) { stackA.push(temp); } else { // 若為運算符,則依次彈出 A 棧頂兩個數據,並根據運算符進行計算,計算結果重新存入 A 棧 // 此處順序要注意,與後綴有區別 String num2 = stackA.pop(); String num = stackA.pop(); stackA.push(calculate(num, num2, temp)); } } // 掃描結束後,A 棧最終結果即為 表達式結果 return stackA.pop(); } /** * 中綴表達式轉前綴表達式(從右到左掃描表達式) * @param expression 中綴表達式 * @return 前綴表達式 */ public List<String> infixToPrefix(List<String> expression) { Stack<String> stackA = new Stack<>(); // 用於保存 操作符(運算符),簡稱 A 棧 Stack<String> stackB = new Stack<>(); // 用於保存 中間結果(存儲數據以及運算符,存儲過程中不會有出棧操作),簡稱 B 棧 List<String> result = new ArrayList<>(); // 用於記錄最終結果 // 從右到左掃描表達式,取出數據、運算符 並計算 for (int i = expression.size() - 1; i >= 0; i--) { // 用於表示集合當前取出的數據 String temp = expression.get(i); // 如果取出的為 操作數,直接存入 B 棧 if (temp.matches("\\d+")) { stackB.push(temp); } else { // 如果取出的是左括號 if ("(".equals(temp)) { // 依次彈出 A 棧頂元素並壓入 B 棧,直至遇到 右括號 ")" while(stackA.size() > 0 && !")".equals(stackA.peek())) { stackB.push(stackA.pop()); } // 移除 A 棧頂右括號 ")" stackA.pop(); } else { // 比較運算符優先級,判斷運算符直接進入 A 棧 還是 先彈出 A 棧頂元素並壓入 B 棧後、再將當前運算符入 A 棧 while(true) { // 如果當前運算符為右括號 ")" 或者 A 棧為空 或者 A 棧頂元素為右括號 ")" 或者 當前運算符優先級 高於 A 棧頂運算符,則直接入 A 棧 if (")".equals(temp) || stackA.size() == 0 || ")".equals(stackA.peek()) || priority(temp) > priority(stackA.peek())) { stackA.push(temp); break; } // 若上麵條件均不滿足,即當前運算符優先級小於等於 A 棧頂運算符,則彈出 A 棧頂運算符並壓入 B 棧 stackB.push(stackA.pop()); } } } } // 依次將 A 棧剩餘元素彈出並壓入到 B 棧 while(stackA.size() > 0) { stackB.push(stackA.pop()); } // 依次取出 B 棧元素,即為 前綴表達式 while(stackB.size() > 0) { result.add(stackB.pop()); } return result; } /** * 中綴表達式轉後綴表達式(從左到右掃描表達式) * @param expression 中綴表達式 * @return 後綴表達式 */ public List<String> infixToSuffix(List<String> expression) { Stack<String> stackA = new Stack<>(); // 用於保存 操作符(運算符),簡稱 A 棧 // Stack<String> stackB = new Stack<>(); // 用於保存 中間結果,簡稱 B 棧 // 由於 B 棧反序輸出才是後綴表達式,此處可以直接存放在 集合中,順序讀取即為 後綴表達式。 List<String> result = new ArrayList<>(); // 用於保存 最終結果,此處用來替代 B 棧,後面簡稱 B 棧。 // 從左到右掃描後綴表達式 expression.forEach(x -> { // 如果取出的是 操作數,直接存入 B 棧 if (x.matches("\\d+")) { result.add(x); } else { // 如果操作符是右括號 ")" if (")".equals(x)) { // 依次將 A 棧頂運算符彈出 並壓入 B 棧,直至遇到左括號 "(" while(stackA.size() > 0 && !"(".equals(stackA.peek())) { result.add(stackA.pop()); } // 移除 A 棧頂左括號 "(" stackA.pop(); } else { // 比較運算符優先級,判斷運算符直接進入 A 棧 還是 先彈出 A 棧頂元素並壓入 B 棧後、再將當前運算符入 A 棧 while(true) { // 如果當前運算符為左括號 "(" 或者 A 棧為空 或者 A 棧頂運算符為左括號 "(" 或者 當前運算符優先級 高於 A 棧頂運算符,則直接入 A 棧 if ("(".equals(x) || stackA.size() == 0 || "(".equals(stackA.peek()) || priority(x) > priority(stackA.peek())) { stackA.push(x); break; } // 如果上麵條件均不滿足,即當前運算符 優先級 小於或等於 A 棧頂運算符 // 則將 A 棧頂運算符取出並 放入 B 棧 result.add(stackA.pop()); } } } }); // 依次將 A 棧頂運算符取出放入 B 棧 while(stackA.size() > 0) { result.add(stackA.pop()); } return result; } /** * 後綴表達式求值(從左到右掃描表達式) * @param expression 後綴表達式 * @return 計算結果 */ public String suffixExpression(List<String> expression) { Stack<String> stackA = new Stack<>(); // 用於保存 操作數,簡稱 A 棧 // 從左到右掃描表達式 expression.forEach(x -> { // 如果是 數字,直接進 A 棧 if (x.matches("\\d+")) { stackA.push(x); } else { // 是運算符,則取出 A 棧頂兩元素,並計算,將計算結果重新壓入 A 棧 stackA.push(calculate(stackA.pop(), stackA.pop(), x)); } }); // 掃描結束後,A 棧最終結果即為 表達式結果 return stackA.pop(); } } 【輸出結果:】 當前表達式為: (13-6)*5-6 ================================ 表達式轉換後為中綴表達式: [(, 13, -, 6, ), *, 5, -, 6] ================================ 中綴表達式求值為: 29 ================================ 中綴表達式: [(, 13, -, 6, ), *, 5, -, 6] 轉為 前綴表達式: [-, *, -, 13, 6, 5, 6] 前綴表達式求值為: 29 ================================ 中綴表達式: [(, 13, -, 6, ), *, 5, -, 6] 轉為 後綴表達式: [13, 6, -, 5, *, 6, -] 後綴表達式求值為: 29 ================================
7、遞歸與回溯、八皇后問題
(1)遞歸:
遞歸指的是 方法調用自身方法去解決問題的過程。
其目的是 將一個複雜的大問題 轉換為 與原問題類似的小問題去求解。遞歸必須得有結束條件,否則將會陷入無限遞歸(導致棧溢出異常)。
常用場景:快排、歸併排序、二分查找、漢諾塔、八皇后 等問題。
(2)回溯:
回溯指的是 類似枚舉的選優搜索過程,當條件不符合時,返回上一層(即回溯)重新判斷。
其解決的是 某種場景下有許多個解,依次判斷每個解是否合適,如果不合適就回退到上一層,重新判斷下一個解是否合適。
常見場景:八皇后 問題。
(3)八皇后問題分析
【八皇后問題介紹:】 在一個 8 * 8 的國際象棋棋盤上,擺放 八個皇后,且皇后之間不能相互攻擊,總共有多少種擺法。 不能相互攻擊 即: 任意兩個皇后 不能同時 處在 同一行、同一列、同一斜線上。 【思路分析:】 採用 回溯 方法解決。 每次放置皇后時,均從每行的第一列開始嘗試,並校驗該皇后位置是否與其他皇后位置發生衝突,如果不衝突則遞歸調用下一個皇后進行放置, 如果衝突則嘗試當前皇后位置的下一個位置是否能夠放置,若當前皇后在當前行的所有列均放置失敗,則回溯到上一個皇后所處位置,使上一個皇后放置在其下一列 並重新判斷該位置是否衝突。 即: Step1:第一個皇后放在第一行第一列。 Step2:第二個皇后放在第二行第一列,判斷是否會攻擊,如果會攻擊,則將 第二個皇后放在第二行第二列 進行判斷。 若仍會攻擊,則依次放置下去,直至第二行第八列。若仍會攻擊,則後續不用執行(此時第二個皇后 8 個位置均放置失敗),回溯到 上一行 並再次枚舉。 Step3:第二個皇后放好後,同理放置第三個皇后 直至 放置第八個 皇后,若均不衝突則 為一個解。 【判斷皇后之間是否攻擊:】 使用一維數組 a[8] 存儲可行的 八皇后 放置位置(二維數組亦可)。 每一個數組元素存儲範圍為 0~7,分別表示第 1 ~ 8 位置。 判斷皇后之間是否攻擊:設當前為第 n 個皇后,記為 a[n]。 同一行:不需要考慮,每次都是不同行。 同一列:遍歷一維數組,如果 a[i] == a[n],則表示當前存在攻擊。 for(int i = 0; i < n; i++) { if (a[i] == a[n]) { return false; } } 同一斜線:遍歷一維數組,若 Math.abs(n - i) == Math.abs(a[n] - a[i]),則存在攻擊。 for(int i = 0; i < n; i++) { if (Math.abs(n - i) == Math.abs(a[n] - a[i])) { return false; } } 註: i 指的是第 i+1 個皇后,a[i] 指的是第 i+1 個皇后所佔據的位置(0~7)。 所以 a[i] == a[n] 時表示同一列。 Math.abs(n - i) == Math.abs(a[n] - a[i]) 表示同一斜線(看成等腰直角三角形)。

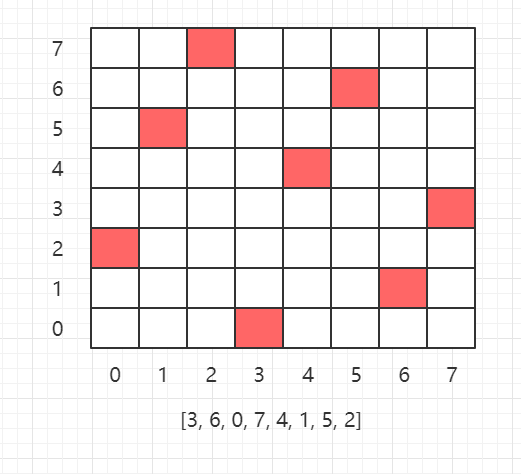
【八皇后代碼實現:】 package com.lyh.recursion; import java.util.Arrays; public class EightQueens { private int maxsize = 8; // 定義最大為 8 皇后 private int count = 0; // 用於記錄皇后放置總解法數 private int[] arrays = new int[maxsize]; // 用於存儲 8 皇后的解法,範圍為 0 ~ 7,表示第 1 ~ 8 位置 public EightQueens() { } public EightQueens(int maxsize) { this.maxsize = maxsize; arrays = new int[this.maxsize]; } public static void main(String[] args) { EightQueens eightQueens = new EightQueens(); eightQueens.putQueen(0); System.out.println("總解法: " + eightQueens.count); } /** * 檢查當前皇后的放置位置 是否 與其他皇后位置衝突 * @param n 當前為第 n+1 皇后 * @return true 表示不衝突 */ public boolean check(int n) { // 遍歷當前所有皇后,已放置 0 ~ n-1 個皇后,即 第 1 ~ n 皇后位置 for(int i = 0; i < n; i++) { // arrays[i] == arrays[n] 表示兩皇后在同一列 // Math.abs(n - i) == Math.abs(arrays[n] - arrays[i]) 表示兩皇后在同一斜線上(看成等腰直角三角形處理) if (arrays[i] == arrays[n] || Math.abs(n - i) == Math.abs(arrays[n] - arrays[i])) { return false; } } return true; } /** * 遞歸 + 回溯 放置皇后 * @param n 第 n+1 個皇后 */ public void putQueen(int n) { // 所有皇后放置完成,打印皇后放置方法 // 此處為第一個出口,即 8 個皇后全部放置完成時。 if (n == maxsize) { System.out.println(Arrays.toString(arrays)); count++; return; } // 枚舉依次求解,遍歷 0 ~ maxsize - 1,表示當前皇后放置在第 1 ~ maxsize 個位置。 // 此處為第二個出口,若遍歷完成,n 仍不為 8,即 第 n-1 個皇后 8 個位置均放置失敗,後續無需再做,回溯到上一個皇后放置位置的下一個位置 for (int i = 0; i < maxsize; i++) { // 放置皇后 arrays[n] = i; // 當前皇后放置不衝突,則放置下一個皇后,若衝突則結束當前循環並判斷下一個位置是否衝突 if (check(n)) { putQueen(n + 1); } } } } 【輸出結果:】 [0, 4, 7, 5, 2, 6, 1, 3] [0, 5, 7, 2, 6, 3, 1, 4] [0, 6, 3, 5, 7, 1, 4, 2] [0, 6, 4, 7, 1, 3, 5, 2] [1, 3, 5, 7, 2, 0, 6, 4] [1, 4, 6, 0, 2, 7, 5, 3] [1, 4, 6, 3, 0, 7, 5, 2] [1, 5, 0, 6, 3, 7, 2, 4] [1, 5, 7, 2, 0, 3, 6, 4] [1, 6, 2, 5, 7, 4, 0, 3] [1, 6, 4, 7, 0, 3, 5, 2] [1, 7, 5, 0, 2, 4, 6, 3] [2, 0, 6, 4, 7, 1, 3, 5] [2, 4, 1, 7, 0, 6, 3, 5] [2, 4, 1, 7, 5, 3, 6, 0] [2, 4, 6, 0, 3, 1, 7, 5] [2, 4, 7, 3, 0, 6, 1, 5] [2, 5, 1, 4, 7, 0, 6, 3] [2, 5, 1, 6, 0, 3, 7, 4] [2, 5, 1, 6, 4, 0, 7, 3] [2, 5, 3, 0, 7, 4, 6, 1] [2, 5, 3, 1, 7, 4, 6, 0] [2, 5, 7, 0, 3, 6, 4, 1] [2, 5, 7, 0, 4, 6, 1, 3] [2, 5, 7, 1, 3, 0, 6, 4] [2, 6, 1, 7, 4, 0, 3, 5] [2, 6, 1, 7, 5, 3, 0, 4] [2, 7, 3, 6, 0, 5, 1, 4] [3, 0, 4, 7, 1, 6, 2, 5] [3, 0, 4, 7, 5, 2, 6, 1] [3, 1, 4, 7, 5, 0, 2, 6] [3, 1, 6, 2, 5, 7, 0, 4] [3, 1, 6, 2, 5, 7, 4, 0] [3, 1, 6, 4, 0, 7, 5, 2] [3, 1, 7, 4, 6, 0, 2, 5] [3, 1, 7, 5, 0, 2, 4, 6] [3, 5, 0, 4, 1, 7, 2, 6] [3, 5, 7, 1, 6, 0, 2, 4] [3, 5, 7, 2, 0, 6, 4, 1] [3, 6, 0, 7, 4, 1, 5, 2] [3, 6, 2, 7, 1, 4, 0, 5] [3, 6, 4, 1, 5, 0, 2, 7] [3, 6, 4, 2, 0, 5, 7, 1] [3, 7, 0, 2, 5, 1, 6, 4] [3, 7, 0, 4, 6, 1, 5, 2] [3, 7, 4, 2, 0, 6, 1, 5] [4, 0, 3, 5, 7, 1, 6, 2] [4, 0, 7, 3, 1, 6, 2, 5] [4, 0, 7, 5, 2, 6, 1, 3] [4, 1, 3, 5, 7, 2, 0, 6] [4, 1, 3, 6, 2, 7, 5, 0] [4, 1, 5, 0, 6, 3, 7, 2] [4, 1, 7, 0, 3, 6, 2, 5] [4, 2, 0, 5, 7, 1, 3, 6] [4, 2, 0, 6, 1, 7, 5, 3] [4, 2, 7, 3, 6, 0, 5, 1] [4, 6, 0, 2, 7, 5, 3, 1] [4, 6, 0, 3, 1, 7, 5, 2] [4, 6, 1, 3, 7, 0, 2, 5] [4, 6, 1, 5, 2, 0, 3, 7] [4, 6, 1, 5, 2, 0, 7, 3] [4, 6, 3, 0, 2, 7, 5, 1] [4, 7, 3, 0, 2, 5, 1, 6] [4, 7, 3, 0, 6, 1, 5, 2] [5, 0, 4, 1, 7, 2, 6, 3] [5, 1, 6, 0, 2, 4, 7, 3] [5, 1, 6, 0, 3, 7, 4, 2] [5, 2, 0, 6, 4, 7, 1, 3] [5, 2, 0, 7, 3, 1, 6, 4] [5, 2, 0, 7, 4, 1, 3, 6] [5, 2, 4, 6, 0, 3, 1, 7] [5, 2, 4, 7, 0, 3, 1, 6] [5, 2, 6, 1, 3, 7, 0, 4] [5, 2, 6, 1, 7, 4, 0, 3] [5, 2, 6, 3, 0, 7, 1, 4] [5, 3, 0, 4, 7, 1, 6, 2] [5, 3, 1, 7, 4, 6, 0, 2] [5, 3, 6, 0, 2, 4, 1, 7] [5, 3, 6, 0, 7, 1, 4, 2] [5, 7, 1, 3, 0, 6, 4, 2] [6, 0, 2, 7, 5, 3, 1, 4] [6, 1, 3, 0, 7, 4, 2, 5] [6, 1, 5, 2, 0, 3, 7, 4] [6, 2, 0, 5, 7, 4, 1, 3] [6, 2, 7, 1, 4, 0, 5, 3] [6, 3, 1, 4, 7, 0, 2, 5] [6, 3, 1, 7, 5, 0, 2, 4] [6, 4, 2, 0, 5, 7, 1, 3] [7, 1, 3, 0, 6, 4, 2, 5] [7, 1, 4, 2, 0, 6, 3, 5] [7, 2, 0, 5, 1, 4, 6, 3] [7, 3, 0, 2, 5, 1, 6, 4] 總解法: 92
三、排序算法
1、常見內排序
之前總結過一篇,此處不重複介紹,對其稍作補充說明。
詳見://www.cnblogs.com/l-y-h/p/12391241.html
2、基數排序(Radix Sort)
(1)什麼是基數排序?
基數排序是桶排序的擴展,其將 整數 按照 位數(個位、十位、百位等)進行劃分,每次劃分後將劃分的結果存放到相應的桶中,最終達到排序的目的。
基數排序屬於穩定排序。
【基數排序步驟:(此時無法處理負數)】 Step1:首先定義一個桶數組,編號為 0 ~ 9,分別表示用於存儲符合 0 ~ 9 的數據。 且每個桶元素 又是一個數組,用於存儲符合 0 ~ 9 的數據。 Step2:對於一組數據,從每個數的 個位 開始進行劃分(個位範圍為 0 ~ 9),將數據分別存儲到 桶數組中。 然後遍歷輸出得到新的數組。 Step3:對於新的一組數據,從每個數的 十位 開始劃分,進行 Step2 同樣操作。 Step4:同理,處理 百位、千位,若一個數沒有 百位、千位,則將其視為 0 處理。 註: 首先得獲取當前數據中 最大數據 的位數,然後再進行 位數劃分。 比如: 7 99 10 8 中最大數據為 兩位數,需進行 個位、十位 劃分。 45 123 34 中最大數據為 三位數,需進行 個位、十位、百位 劃分。 【基數排序存在 負數 時處理:】 可以先找到 負數的最小值,然後將所有數據 整體加上 負數最小值的絕對值 加 1,記為 min = |負數最小值|, 即 讓所有數據均變為 非負數,然後再去排序,最後將結果 再整體減去 min 即可。 註: 若 最大值、最小值 瀕臨極限時,可能會造成數據溢出(此時慎用)。 【給數據 arr {38, 65, 97, 76, 13, 27, 49} 排序,並按照從小到大的順序輸出】 Step1:首先定義一個 二維數組 a[10][arr.length] 表示桶,分別用於存儲符合 0 ~ 9 的數據。 Step2:按照 個位 進行劃分。 38 個位為 8,進入 a[8] 桶。 65 個位為 5,進入 a[5] 桶。 97 個位為 7,進入 a[7] 桶。 76 個位為 6,進入 a[6] 桶。 13 個位為 3,進入 a[3] 桶。 27 個位為 7,進入 a[7] 桶。 49 個位為 9,進入 a[9] 桶。 即: 0 1 2 3 13 4 5 65 6 76 7 97 27 8 38 9 49 依次取出桶中元素,存入新數組中。即 {13, 65, 76, 97, 27, 38, 49} Step3:根據新數組按照 十位 進行劃分。 13 十位為 1,進入 a[1] 桶。 65 十位為 6,進入 a[6] 桶。 76 十位為 7,進入 a[7] 桶。 97 十位為 9,進入 a[9] 桶。 27 十位為 2,進入 a[2] 桶。 38 十位為 3,進入 a[3] 桶。 49 十位為 4,進入 a[4] 桶。 即: 0 1 13 2 27 3 38 4 49 5 6 65 7 76 8 9 97 依次取出桶中元素,存入新數組中。即 {13, 27, 38, 49, 65, 76, 97}
(2)代碼實現
【代碼實現:】 package com.lyh.sort; import java.util.Arrays; public class RadixSort { public static void main(String[] args) { int[] arrays = new int[]{38, 65, 97, 76, 13, 27, 49}; radixSort(arrays); System.out.println("===================="); // int[] arrays = new int[]{38, 65, 0, -1, 13, 27, 49}; int[] arrays2 = new int[]{38, 65, 0, -1, 13, 27, -10}; radixSort(arrays2); } /** * 基數排序(包括負數排序) * @param arrays 待排序數組 */ public static void radixSort(int[] arrays) { // 判斷數組是否合法 if (arrays.length <= 0) { System.out.println("數據為空"); return; } // 獲取當前數據中最大值、最小值 int max = arrays[0]; int min = arrays[0]; for (int array : arrays) { if (max < array) { max = array; } if (min > array) { min = array; } } // min 小於 0,即當前存在負數,則將所有數據 加上 min 的絕對值,使其變為非負數 if (min < 0) { for (int i = 0; i < arrays.length; i++) { arrays[i] -= min; } max -= min; } // 定義二維數組,用於表示 桶,存儲數據,bucket[0] ~ bucket[9] 分別用於存儲 0 ~ 9 的數據 int[][] bucket = new int[10][arrays.length]; // 定義一維數組,用於表示 每個桶存儲 數據的個數,bucketCount[0] ~ bucketCount[9] 分別用於存儲 bucket[0] ~ bucket[9] 中數據的個數 int[] bucketCount = new int[10]; // 獲取當前 最大值 的位數,根據 位數 確定需要進行 幾次 數據劃分操作 int maxLength = (max + "").length(); // 根據位數,按照 個位、十位、百位、千位 的順序進行劃分 for (int i = 0, m = 1; i < maxLength; i++, m *= 10) { // 遍曆數組,將數據劃分到 桶中存儲 for (int j = 0; j < arrays.length; j++) { int temp = arrays[j] / m % 10; // 獲取 個位、十位、百位 的值 bucket[temp][bucketCount[temp]++] = arrays[j]; // 桶存儲數據,相應的 bucketCount 也要加 1 } int index = 0; // 用於記錄新數組最後一個值的索引 // 遍歷桶,取出數據組成新的數組, k < bucketCount.length 或者 k < bucket[0].length 均可,都表示 10(0 ~ 9) for (int k = 0; k < bucketCount.length; k++) { // 當前桶存在數據時,取出數據存入數組中,並將該桶置空 // 此處只需將 bucketCount 相應位置置 0 即可(無需將 bucket 置空,每次存儲數據時均會覆蓋,儘管會存在無用值,但無影響) if (bucketCount[k] > 0) { // 將桶元素複製到新數組中 // 源數組 bucket[k], 開始位置 0, 目標數組 arrays,目標數組起始位置 index,複製源數組的數據個數 bucketCount[k] System.arraycopy(bucket[k],0, arrays, index, bucketCount[k]); index += bucketCount[k]; // 當前桶記錄清空 bucketCount[k] = 0; } } System.out.println("第 " + (i + 1) + " 次劃分結果: " + Arrays.toString(arrays)); } // 如果存在負數,則需要減去 相應的值 if (min < 0) { for (int i = 0; i < arrays.length; i++) { arrays[i] += min; } } System.out.println("最終排序結果為: " + Arrays.toString(arrays)); } } 【輸出結果:】 第 1 次劃分結果: [13, 65, 76, 97, 27, 38, 49] 第 2 次劃分結果: [13, 27, 38, 49, 65, 76, 97] 最終排序結果為: [13, 27, 38, 49, 65, 76, 97] ==================== 第 1 次劃分結果: [10, 0, 23, 75, 37, 48, 9] 第 2 次劃分結果: [0, 9, 10, 23, 37, 48, 75] 最終排序結果為: [-10, -1, 0, 13, 27, 38, 65]
(3)分析:
若數據中出現相同的值,且向桶存放數據以及從桶取數據的過程中不會出現交換值的情況,故排序是穩定的。
每次均會遍曆數據 n,且最大位數為 k,即 時間複雜度為 O(n*k)。
需要使用二維數組存儲 桶元素,使用一維數組存儲 桶存儲元素個數,即空間複雜度為 O(10 * n + 10),即空間複雜度為 O(n)。
四、查找算法
1、順序(線性)查找
(1)什麼是 線性查找?
最簡單直接的一種查找方式,基本思想是 對於待查找數據 key, 從數據的第一個記錄開始,逐個 與 key 比較,若存在與 key 相同的值則查找成功,若不存在則查找失敗。
(2)代碼實現
【代碼實現:】 package com.lyh.search; public class LinearSearch { public static void main(String[] args) { int[] arrays = new int[]{100, 40, 78, 24, 10, 16}; int key = 10; int index = linearSearch(arrays, key); if (index != -1) { System.out.println("查找成功,下標為: " + index); } else { System.out.println("查找失敗"); } } /** * 順序查找,返回元素下標 * @param arrays 待查找數組 * @param key 待查找數據 * @return 查找失敗返回 -1,查找成功返回 0 ~ n-1 */ public static int linearSearch(int[] arrays, int key) { // 遍曆數組,挨個匹配 for (int i = 0; i < arrays.length; i++) { if (arrays[i] == key) { return i; } } return -1; } } 【輸出結果:】 查找成功,下標為: 4
(3)分析
順序查找效率是比較低的,n 個數據最壞情況下需要比較 n 次,即時間複雜度為 O(n)。
2、二分(折半)查找
(1)什麼是 折半查找?
是一個效率較高的查找方法。其要求必須採用 順序存儲結構 且 存儲數據有序。
【基本實現思路:】 Step1:確定數組的中間下標。 middle = (left + right) / 2。將數據 分為左右兩部分。 Step2:將待查找數據 key 與 中間元素 arrays[middle] 比較。 Step2.1:如果 key > arrays[middle],則說明要查找數據在 middle 下標右側,需要在右側數據進行查找(遞歸)。 Step2.2:如果 key < arrays[middle],則說明要查找數據在 middle 下標左側,需要在左側數據進行查找(遞歸)。 Step2.3:如果 key == arrays[middle],則說明查找成功。 上面遞歸結束條件: 查找成功,結束遞歸。 查找失敗,即 left > right 時,退出遞歸。 【舉例:】 在 {13, 27, 38, 49, 65, 76, 97} 中查找 key = 27。 第一次折半: left = 0, right = 6, middle = 3 即 a[left] = 13, a[right] = 97, a[middle] = 49。 由於待查找數據 key < a[middle],則從左側剩餘數據 {13, 27, 38, 49} 開始查找。 第二次折半: left = 0, right = 2, middle = 1 即 a[left] = 0, a[right] = 38, a[middle] = 27。 由於待查找數據 key == a[middle],則查找成功。
(2)代碼實現
【代碼實現:】 package com.lyh.search; public class BinarySearch { public static void main(String[] args) { int[] arrays = new int[]{13, 27, 38, 49, 65, 76, 97}; int key = 27; int index = binarySearch(arrays, 0, arrays.length - 1, key); if (index != -1) { System.out.println("查找成功,下標為: " + index); } else { System.out.println("查找失敗"); } } /** * 折半查找,返回元素下標 * @param arrays 待查找數組 * @param left 最左側下標 * @param right 最右側下標 * @param key 待查找數據 * @return 查找失敗返回 -1,查找成功返回元素下標 0 ~ n */ public static int binarySearch(int[] arrays, int left, int right, int key) { // 若 left > right,則表示查找失敗 if (left <= right) { // 獲取中間下標 int middle = (left + right) / 2; if (key == arrays[middle]) { return middle; } else if (key > arrays[middle]) { return binarySearch(arrays, middle + 1, right, key); } else { return binarySearch(arrays, left, middle - 1, key); } } return -1; } } 【輸出結果:】 查找成功,下標為: 1
(3)分析:
每次查找數據均折半,設折半次數為 x,則 2^x = n,即折半次數為 x = logn,時間複雜度為 O(logn)。效率比順序查找高。
3、插值查找
(1)什麼是插值查找?
插值查找類似於 折半查找,其區別在於 中間節點 是自適應的。
採用自適應節點是為了 使 middle 值更靠近 key,從而 減少 key 比較次數。
【插值查找、折半查找區別:】 折半查找 求 middle: middle = (left + right) / 2 = left + (right - left) / 2. 插值查找 求 middle: middle = left + (right - left) * (key - a[left]) / (a[right] - a[left]). 即 使用 (key - a[left]) / (a[right] - a[left]) 去替換 1 / 2,可以在某種情況下提高查找效率。 對於數據量較大、且數據分佈較均勻的 數據來說,使用 插值查找 速度較快(較少比較次數)。 註: 除法可能會遇到異常(java.lang.ArithmeticException: / by zero)。 【舉例:】 對於 0 ~ 99 的數,查找 27, 若採用 折半查找,需要折半 5 次。 若採用 插值查找,需要折半 1 次。
(2)代碼實現
【代碼實現:】 package com.lyh.search; public class InsertionSearch { public static void main(String[] args) { int[] arrays = new int[100]; for(int i = 0; i < arrays.length; i++) { arrays[i] = i; } int key = 27; int index = insertionSearch(arrays, 0, arrays.length - 1, key); if (index != -1) { System.out.println("查找成功,下標為: " + index); } else { System.out.println("查找失敗"); } } /** * 插值查找,返回元素下標 * @param arrays 待查找數組 * @param left 最左側下標 * @param right 最右側下標 * @param key 待查找數據 * @return 查找失敗返回 -1,查找成功返回元素下標 0 ~ n */ public static int insertionSearch(int[] arrays, int left, int right, int key) { // 數據不符合時,退出遞歸 if (left > right || key > arrays[right] || key < arrays[left]) { return -1; } // 自適應節點 int middle = left + (right - left) * (key - arrays[left]) / (arrays[right] - arrays[left]); if (key == arrays[middle]) { return middle; } else if (key > arrays[middle]) { return insertionSearch(arrays, middle + 1, right, key); } else { return insertionSearch(arrays, left, middle + 1, key); } } } 【輸出結果:】 查找成功,下標為: 27
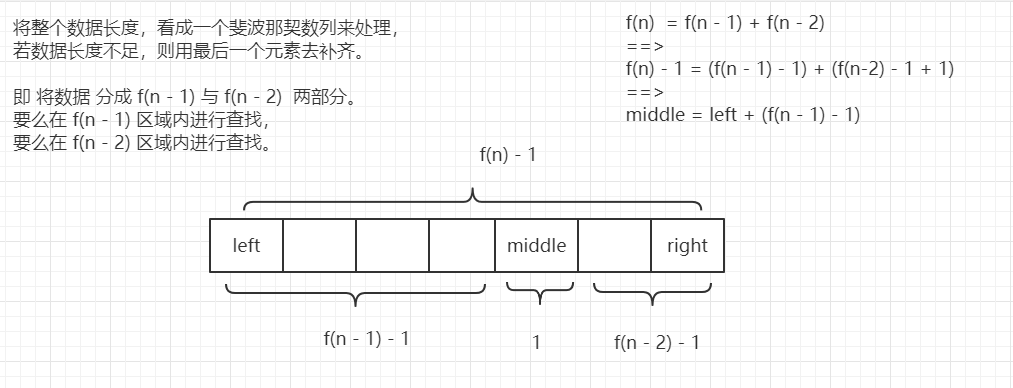
4、斐波那契(黃金分割)查找
(1)什麼是 斐波那契 查找?
斐波那契查找 與 折半查找、插值查找 類似,都是改變中間節點的位置。
此時的 中間節點 位於 黃金分割點 附近。
【黃金分割比例:】 黃金分割比例指 將一個整體分為兩個部分,其中 較小部分 : 較大部分 = 較大部分 : 整體,且值約為 0.618,此比例稱為黃金分割比例。 比如: 1 米長繩子,分為 0.618 與 0.382 兩部分,則 0.382 :0.618 == 0.618 :1。 【斐波那契數列:】 斐波那契公式: f(1) = 1; f(2) = 1; f(n) = f(n - 1) + f(n - 2); n > 2 即:數列 {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...} 斐波那契數列兩個相鄰數的比例,近似於 0.618。 比如: 21 : 34 == 0.6176470588235294 : 1 34 : 55 == 0.6181818181818182 : 1 【斐波那契查找算法原理:】 如何求黃金分割點: 由於斐波那契數列公式為 f(n) = f(n - 1) + f(n - 2), 且 f(n -1 ) : f(n - 2) == 0.618。 想要使用 斐波那契處理 數據,即將數據按照 f(n-1) 與 f(n-2) 分成兩部分即可。 比如:f(n) - 1 = (f(n - 1) - 1) + (f(n - 2) - 1 + 1); 分為 (f(n - 1) - 1) 與 (f(n - 2) - 1 + 1) 兩部分。 此時 left + (f(n - 1) - 1) 即為黃金分割點 middle。 斐波那契查找: 其將一組數據長度 看成是 斐波那契數列 進行處理,若當前數據長度 不滿足 斐波那契數列,則使用 最後一個元素將其補齊。 長度符合後,記新數組為 temp,根據 middle 計算出中間節點,並進行判斷。 若 key > temp[middle],則需要在右側進行遞歸判斷,而此時右側屬於 f(n - 2) 部分,即 k = k - 2; 若 key < temp[middle],則需要在左側進行遞歸判斷,而此時左側屬於 f(n - 1) 部分,即 k = k - 1; 若 key == temp[middle],則查找成功。 【舉例:】 在 {13, 27, 38, 49, 65, 76, 97} 中查找 key = 27。 Step1:補齊數據。 當前數據 arrays 長度為 7,而與之相近的斐波那契數列值為 8(f(n) = 8, n = 5),需要將其補齊。 即數據變為 temp = {13, 27, 38, 49, 65, 76, 97, 97}. Step2:開始第一次查找操作,中間節點 middle = left + (f(n - 1) - 1) left = 0,right = 7,n = 5,middle = 4, key < temp[middle],即下次在左側 {13, 27, 38, 49} 進行查找(right = middle - 1 = 3)。 左側部分等同於 f(n - 1) 區,所以 n 減 1, 即 n = 4。 Step3:開始第二次查找, left = 0, right = 3,n = 4, middle = 2 key < temp[middle],即下次在左側 {13, 27} 進行查找(right = middle - 1 = 1)。 左側部分等同於 f(n - 1) 區,所以 n 減 1, 即 n = 3。 Step3:開始第三次查找, left = 0, right = 1,n = 3, middle = 1 key == temp[middle],查找成功。
(2)代碼實現
【代碼實現:】 package com.lyh.search; import java.util.Arrays; public class FibonacciSearch { public static void main(String[] args) { int[] arrays = new int[]{13, 27, 38, 49, 65, 76, 97}; int key = 27; int index = fibonacciSearch(arrays, key); if (index != -1) { System.out.println("查找成功,當前下標為: " + index); } else { System.out.println("查找失敗"); } } /** * 返回斐波那契數組(使用 迭代 實現) * @return 斐波那契數組 */ public static int[] fibonacci(int length) { if (length < 0) { return null; } int[] fib = new int[length]; if (length >= 1) { fib[0] = 1; } if (length >= 2) { fib[1] = 1; } for (int i = 2; i < length; i++) { fib[i] = fib[i - 1] + fib[i - 2]; } return fib; } /** * 斐波那契查找,返回對應數據下標 * 將數據長度看成 斐波那契數列,將數據分為 f(n - 1)、 f(n - 2) 兩部分 * @param arrays 待查找數組 * @param key 待查找數據 * @return 查找失敗返回 -1,查找成功返回相應的下標 */ public static int fibonacciSearch(int[] arrays, int key) { int n = 0; // 用於記錄當前 分隔點 下標 int[] fibs = fibonacci(arrays.length); // 用於記錄斐波那契數列 // 獲取第一次分割點下標 while (arrays.length > fibs[n]) { n++; } // 若當前數組長度 不滿足 斐波那契數列,則使用最後一個元素 去填充新數組,使新長度滿足 斐波那契數列 int[] temp = Arrays.copyOf(arrays, fibs[n]); for (int i = arrays.length; i < fibs[n]; i++) { temp[i] = arrays[arrays.length - 1]; } // 開始查找 int left = 0; int right = temp.length - 1; while(left <= right) { // 獲取中間節點,將數據區域分為 f(n - 1), f(n - 2) 兩部分 int middle = left + fibs[n - 1] - 1; if (key == temp[middle]) { // 查找成功 return middle; } else if (key > temp[middle]) { // 當前查找失敗,下次在右側 f(n - 2) 區域進行查找 left = middle + 1; n -= 2; } else { // 當前查找失敗,下次在左側 f(n - 1) 區域進行查找 right = middle - 1; n -= 1; } } // 查找失敗,即 left > right,返回 -1 return -1; } } 【輸出結果:】 查找成功,當前下標為: 1
四、哈希表、樹
1、哈希表(散列表)
(1)什麼是哈希表?
哈希表是一種 根據 關鍵碼(key) 直接訪問值(value)的 一種數據映射結構。其通過一個映射函數,將 關鍵碼 映射到 表中的某一個位置 進行訪問(可以提高查找速度)。
哈希表可以使用 數組 + 鏈表、 或者 數組 + 二叉樹 的形式實現。
適用於 查詢性能要求高、數據之間無邏輯關係 的場景。
【數組 + 鏈表 形式實現哈希表:】 基本結構: 使用 數組(連續的存儲空間) 表示一個散列表。 每個數組元素 存儲的 是一個 單鏈表(用於存儲 映射函數 相同的值)。 即 鏈表數組,定義一個 鏈表結構,在用其 定義數組。 基本過程: 對於一個數,通過 散列函數(hash(),可以通過 取模 或者 位運算) 計算 key,並將其映射到 散列表(數組)的 某個位置。 對於相同的 hash 值(產生 hash 衝突),通常採用 拉鏈法來解決。 簡單地講,就是將 hash(key) 得到的結果 作為 數組的下標,若多個 key 的 hash(key) 相同,那麼在當前數組下標的位置建立一個鏈表來保存數據。 【數組 + 鏈表 形式實現哈希表 核心代碼結構:】 Step1:定義鏈表節點: /** * 鏈表節點 * @param <K> key * @param <V> value */ class Node<K, V> { K key; // key,用於 散列函數 計算的值 V value; // value,節點真實存儲數據 Node<K, V> next; // 指向下一個節點 public Node(K key, V value) { this.key = key; this.value = value; } } Step2:構建鏈表: /** * 鏈表,用於存儲數據 * @param <K> * @param <V> */ class NodeList<K, V> { Node<K, V> first; // 第一個節點,即存儲真實數據,非頭指針 } Step3:構建鏈表數組,以及散列函數。 /** * 定義 哈希 結構,鏈表數組 * @param <K> * @param <V> */ class HashTable<K, V> { private int size = 16; // 默認大小為 16 NodeList<K, V>[] table; // 鏈表數組,散列函數 確定 數組下標位置,數組元素(鏈表) 用於存儲值 public HashTable() { this(16); } public HashTable(int size) { // 保存哈希表大小 this.size = size; // 構建哈希表(數組) this.table = new NodeList[this.size]; // 初始化每個數組元素 -- 鏈表,否則默認為 null for (int i = 0; i < this.size; i++) { this.table[i] = new NodeList<>(); } } /** * 散列函數,此處以 模運算 為例,可以使用 位運算 * @param key 待計算的 key * @return 哈希值(數組下標) */ public int hash(K key) { return key.hashCode() % size; } } 【實現簡單的增、查:】 添加節點: 首先根據 key 通過 散列函數 計算後,得到 數組下標。 根據數組下標定位到 相應的鏈表,然後進行添加操作。 若當前鏈表為空,則添加數據為第一個節點。 若當前鏈表不空,則遍歷鏈表,若發現相同 key,則替換其 value。 若沒有相同 key,則遍歷到鏈表末尾並添加節點。 查找節點: 同樣根據 key 計算出數組下標,然後定位到相應的鏈表。 遍歷鏈表,並比較 key,若 key 相同則返回 value, 若鏈表遍歷完成仍不存在相同 key 則返回 null。

(2)代碼實現
【代碼實現:】 package com.lyh.tree; public class HashTableDemo { public static void main(String[] args) { HashTable<Integer, String> hashTable = new HashTable<>(4); hashTable.list(); System.out.println("================="); for (int i = 0; i < 10; i++) { hashTable.put(i, i + ""); } hashTable.list(); System.out.println("================="); hashTable.put(1, "Java"); hashTable.put(2, "Python"); hashTable.list(); System.out.println("================="); System.out.println("key = 2 的 value 為: " + hashTable.get(2)); } } /** * 定義 哈希 結構,鏈表數組 * @param <K> * @param <V> */ class HashTable<K, V> { private int size = 16; // 默認大小為 16 NodeList<K, V>[] table; // 鏈表數組,散列函數 確定 數組下標位置,數組元素(鏈表) 用於存儲值 public HashTable() { this(16); } public HashTable(int size) { // 保存哈希表大小 this.size = size; // 構建哈希表(數組) this.table = new NodeList[this.size]; // 初始化每個數組元素 -- 鏈表,否則默認為 null for (int i = 0; i < this.size; i++) { this.table[i] = new NodeList<>(); } } /** * 散列函數,此處以 模運算 為例,可以使用 位運算 * @param key 待計算的 key * @return 哈希值(數組下標) */ public int hash(K key) { return key.hashCode() % size; } /** * 向哈希表中添加數據 * @param key * @param value */ public void put(K key, V value) { // 通過 散列函數 根據 key 計算出 數組下標位置,然後向鏈表中添加數據 this.table[hash(key)].add(key, value); } /** * 查找節點 * @param key 查找條件 * @return 節點數據 */ public V get(K key) { // 通過 散列函數 根據 key 計算出 數組下標位置,然後從鏈表中取出數據 return this.table[hash(key)].find(key); } /** * 輸出哈希表 */ public void list() { // 遍曆數組,輸出每個鏈表 for (int i = 0; i < this.size; i++) { this.table[i].list(i); } } } /** * 鏈表,用於存儲數據 * @param <K> * @param <V> */ class NodeList<K, V> { Node<K, V> first; // 第一個節點,即存儲真實數據,非頭指針 /** * 在鏈表末尾添加節點 * @param key key * @param value value */ public void add(K key, V value) { // 保存數據到 鏈表第一個節點 if (first == null) { first = new Node<>(key, value); return; } Node<K, V> temp = first; // 使用臨時變量保存 第一個節點,用於輔助鏈表遍歷 // 遍歷鏈表到末尾,並添加節點 while(temp.next != null) { // 如果 key 相等,則替換原來的 value if (key.equals(temp.key)) { temp.value = value; return; } temp = temp.next; } temp.next = new Node<>(key, value); } /** * 遍歷輸出鏈表 * @param i 當前數組下標,表示當前為第 i+1 鏈表 */ public void list(int i) { Node<K, V> temp = first; // 使用臨時變量保存 第一個節點,用於輔助鏈表遍歷 // 判斷鏈表是否為空 if (temp == null) { System.out.println("第 " + (i + 1) + " 鏈表為空"); return; } // 遍歷輸出鏈表 System.out.print("第 " + (i + 1) + " 鏈表為: "); while(temp != null) { System.out.print("[ key = " + temp.key + ", value = " + temp.value + " ] ==> "); temp = temp.next; } System.out.println(); } /** * 查找節點 * @param key 查找條件 * @return 查找失敗返回 null,查找成功返回相應節點的 value */ public V find(K key) { Node<K, V> temp = first; // 使用臨時變量保存 第一個節點,用於輔助鏈表遍歷 // 遍歷鏈表,若發現相同 key,則返回 while(temp != null) { if (key.equals(temp.key)) { return temp.value; } temp = temp.next; } return null; } } /** * 鏈表節點 * @param <K> key * @param <V> value */ class Node<K, V> { K key; // key,用於 散列函數 計算的值 V value; // value,節點真實存儲數據 Node<K, V> next; // 指向下一個節點 public Node(K key, V value) { this.key = key; this.value = value; } } 【輸出結果:】 第 1 鏈表為空 第 2 鏈表為空 第 3 鏈表為空 第 4 鏈表為空 ================= 第 1 鏈表為: [ key = 0, value = 0 ] ==> [ key = 4, value = 4 ] ==> [ key = 8, value = 8 ] ==> 第 2 鏈表為: [ key = 1, value = 1 ] ==> [ key = 5, value = 5 ] ==> [ key = 9, value = 9 ] ==> 第 3 鏈表為: [ key = 2, value = 2 ] ==> [ key = 6, value = 6 ] ==> 第 4 鏈表為: [ key = 3, value = 3 ] ==> [ key = 7, value = 7 ] ==> ================= 第 1 鏈表為: [ key = 0, value = 0 ] ==> [ key = 4, value = 4 ] ==> [ key = 8, value = 8 ] ==> 第 2 鏈表為: [ key = 1, value = Java ] ==> [ key = 5, value = 5 ] ==> [ key = 9, value = 9 ] ==> 第 3 鏈表為: [ key = 2, value = Python ] ==> [ key = 6, value = 6 ] ==> 第 4 鏈表為: [ key = 3, value = 3 ] ==> [ key = 7, value = 7 ] ==> ================= key = 2 的 value 為: Python
2、樹
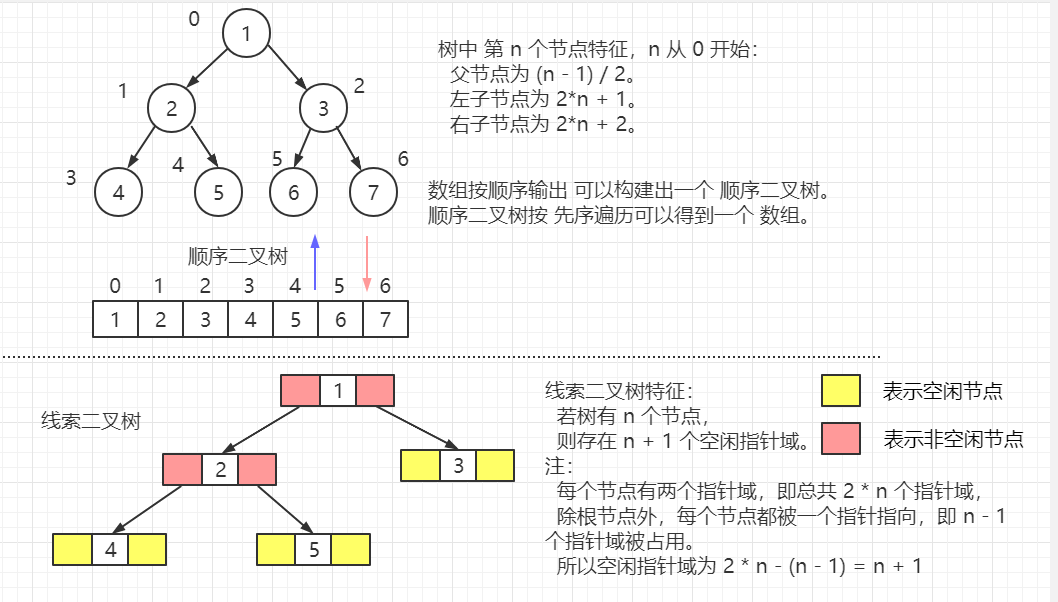
(1)什麼是樹?
樹是一種 由 n 個節點組成的一種 具有層次關係的、類似樹形的 數據結構。
其每個節點 均有 零個或 多個 子節點,每一個節點最多只有一個 父節點,沒有父節點的 節點 稱為 根節點。
(2)為什麼需要樹 這種 數據結構?
前面介紹了 數組、鏈表、以及 哈希表 等數據結構,可以用來存儲數據。
所謂 存在即合理,每種數據結構的出現,必然能解決某種問題,下面分析一下優缺點。
【數組存儲:】 數組採用 連續的 存儲方式來 存儲元素。查詢快、增刪慢。 優點: 可以通過 下標的方式 來訪問(查找)元素,速度快。 且對於有序數組,可以通過 折半查找、插值查找 等方式提高 查找(檢索)效率。 缺點: 對於 插入操作,可能會伴隨着 數組擴容、數組元素整體後移等操作,效率較低。 【鏈表存儲:】 鏈表採用 不連續的 存儲方式來 存儲元素。增刪快、查詢慢。 優點: 插入、刪除節點時,無需整體移動元素,只需要修改 前、後 指針域 即可。效率較高。 缺點: 進行查找時,需要從頭開始遍歷鏈表,若鏈表過長,查詢效率將會較低。 【哈希存儲:】 哈希 採用 數組 + 鏈表 的方式存儲元素,每個 數組元素 存儲的是一個 鏈表。 優點: 其結合了 數組、鏈表 的優點,增、刪、改、查 效率都可以,時間複雜度為 O(1)。 缺點: 由於哈希 存儲的元素是無序的,若想按 順序輸出,實現起來就有點 麻煩。 且哈希只是單次查詢效率高,若執行 n 次查找,時間複雜度將退化到 O(n)。 哈希表由數組實現,擴容也是影響效率的一個問題。 【樹存儲:(以二叉排序樹為例)】 二叉排序樹要求 任何一個 非葉子節點,其左子節點小於 當前節點,其右子節點 大於當前節點。 即 數據是有序的(中序遍歷可得到有序序列)。其在一定程度上保證 增刪 以及 查找的速率 較高。 註: 二叉排序樹可能存在三種定義: 左子節點 小於等於 當前節點,右子節點 大於 當前節點。 左子節點 小於 當前節點,右子節點 大於等於 當前節點。 左子節點 小於 當前節點,右子節點 大於 當前節點。
(3)常見樹分類:
二叉樹、二叉排序樹(BST)、平衡二叉樹(AVL)、2-3 樹、B 樹(B-Tree)、B+ 樹、赫夫曼樹、紅黑樹 等。
3、二叉樹、遍歷二叉樹(遞歸實現 前序、中序、後序 遍歷)
(1)二叉樹基本概念:
二叉樹 是一種要求 每個節點 最多只有 兩個子節點 的樹結構。
註:
樹 轉 數組:
可以通過 前序遍歷、中序遍歷、後序遍歷 三種遍歷形式 遍歷 二叉樹 得到。
數組 轉 樹:
根據 前序遍歷 + 中序遍歷 得到的數組數據 逆向推出 二叉樹。
根據 中序遍歷 + 後序遍歷 得到的數組數據 逆向推出 二叉樹。
根據順序二叉樹的 特點(2*n + 1 、2*n + 2) 構建 順序二叉樹。
【二叉樹常見分類:】 滿二叉樹: 如果 一個 n 層的二叉樹 的所有葉子節點均在最後一層, 且節點總數為 2^n - 1,則該樹為 滿二叉樹。 完全二叉樹: 一棵深度為 k 的有 n 個結點的二叉樹,對樹中的結點按從上至下、從左到右的順序進行編號, 如果編號為 i(1 ≤ i ≤ n)的結點與滿二叉樹中編號為 i 的結點在二叉樹中的位置相同,則這棵二叉樹稱為完全二叉樹。 順序二叉樹: 是二叉樹的一種 存儲形式(按照數組順序,從上到下、從左到右 依次 給二叉樹 添加樹節點,得到一個完全二叉樹 或者 滿二叉樹), 其 可以在 數組 與 樹 之間相互轉換。即 根據一個數組,可以得到 樹 的結構,從樹也可以反推 數組。 特點: 順序二叉樹通常只考慮 完全二叉樹。 其第 n 個元素的左子節點為 2*n + 1。 其第 n 個元素的右子節點為 2*n + 2。 其第 n 個元素的父節點為 (n - 1) / 2。 (n 從 0 開始,即從數組第一個元素下標開始計數)。 線索二叉樹: 對於 n 個節點的 二叉樹,其總共含有 2*n - (n - 1) = n + 1 個空的指針域。 利用這些空的指針域,存放 當前節點 在 某次遍歷(前序、中序、後續)下的 前驅、後繼 節點的指針。 這些指向 前驅、後繼 節點的指針稱為 線索,使用這種線索的二叉樹 稱為線索二叉樹。 即 線索二叉樹的本質 是 將二叉樹 當前節點的空閑指針 改為 指向當前節點 前驅 或者 後繼 節點的過程。 而根據遍歷的分類,前驅、後繼節點會不同,可以分為: 前序線索二叉樹、中序線索二叉樹、後序線索二叉樹。 還有 二叉搜索樹(BST)、平衡二叉搜索樹(AVT)等後續介紹。

(2)二叉樹三種遍歷方式(樹 轉 數組)
樹 轉 數組:
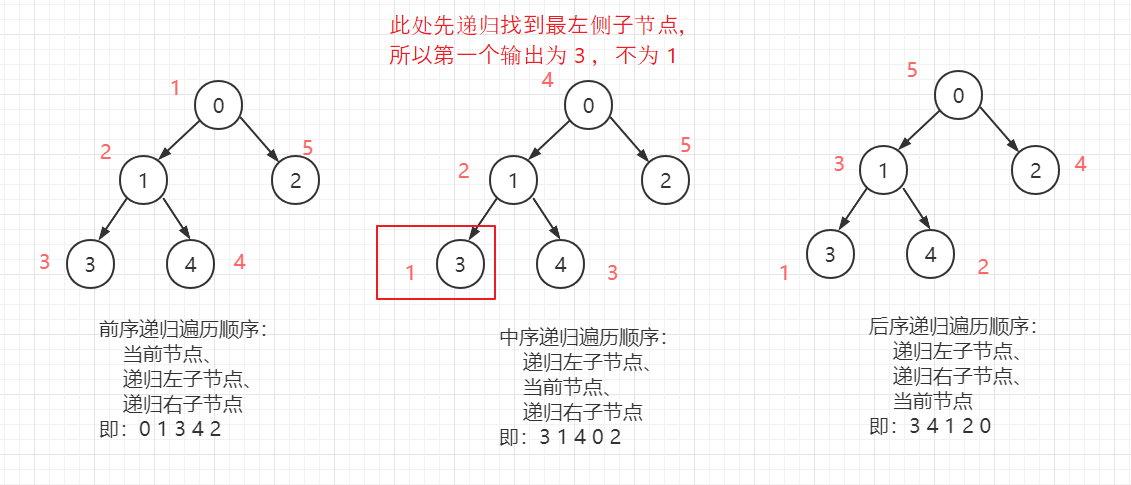
樹 轉 數組,也即 樹的各節點 的遍歷順序,按照 當前節點、左子節點、右子節點 遍歷的先後可以分為三種遍歷:前序遍歷、中序遍歷、後序遍歷。
此時以 遞歸方式實現,後續會補充 迭代實現。
【前序遍歷:】 節點遍歷順序: 先輸出 當前節點,再輸出 左子節點,最後輸出 右子節點。 遍歷、查找步驟: 對於一顆 二叉樹,若二叉樹為空,則直接結束。 否則 輸出 當前節點(若為查找,則在此處進行 值 比較,查找成功則退出)。 前序遍歷 左子樹。 前序遍歷 右子樹。 刪除節點: 刪除的規則可以自定義,不同的規則對應不同的代碼實現。 比如:刪除某帶有左、右子樹的節點,是整體刪除 還是 將子節點 旋轉到當前節點位置。 此處以整體刪除為例: 由於二叉樹是單向的(此處可以理解成 單鏈表 刪除處理), 需要判斷 當前節點的 子節點 是否為待刪除的節點。若是,則直接將當前節點 子節點 置 null 即可。 即: if (this.left.data == key) { this.left = null; return; } if (this.right.data == key) { this.right = null; return; } 【中序遍歷:】 節點遍歷順序: 先輸出 左子節點,再輸出 當前節點,最後輸出 右子節點。 遍歷、查找步驟: 對於一顆 二叉樹,若二叉樹為空,則直接結束。 否則 前序遍歷 左子樹。 輸出 當前節點(若為查找,則在此處進行 值 比較)。 前序遍歷 右子樹。 【後序遍歷:】 節點遍歷順序: 先輸出 左子節點,再輸出 右子節點,最後輸出 當前節點。 遍歷、查找步驟: 對於一顆 二叉樹,若二叉樹為空,則直接結束。 否則 前序遍歷 左子樹。 前序遍歷 右子樹。 輸出 當前節點(若為查找,則在此處進行 值 比較)。 【代碼實現:】 package com.lyh.tree; /** * 構建二叉樹 * @param <K> */ public class BinaryTree<K> { private TreeNode<K> root; // 設置根節點 public BinaryTree(TreeNode<K> root) { this.root = root; } public static void main(String[] args) { // 構建二叉樹 TreeNode<String> root = new TreeNode<>("0"); TreeNode<String> treeNode = new TreeNode<>("1"); TreeNode<String> treeNode2 = new TreeNode<>("2"); TreeNode<String> treeNode3 = new TreeNode<>("3"); TreeNode<String> treeNode4 = new TreeNode<>("4"); root.left = treeNode; root.right = treeNode2; treeNode.left = treeNode3; treeNode.right = treeNode4; // 設置樹 根節點 BinaryTree<String> binaryTree = new BinaryTree<>(root); // 前序遍歷 System.out.print("前序遍歷: "); binaryTree.prefixList(); System.out.println("\n====================="); // 中序遍歷 System.out.print("中序遍歷: "); binaryTree.infixList(); System.out.println("\n====================="); // 後序遍歷 System.out.print("後序遍歷: "); binaryTree.suffixList(); System.out.println("\n====================="); // 前序查找 System.out.print("前序查找, "); TreeNode<String> search = binaryTree.prefixSearch("1"); if (search != null) { System.out.println("查找成功, 當前節點為: " + search + " ,其左節點為: " + search.left + " ,其右節點為: " + search.right); } else { System.out.println("查找失敗"); } System.out.println("\n====================="); // 刪除節點 System.out.print("刪除節點, "); int result = binaryTree.deleteNode("3"); if (result != -1) { System.out.println("成功"); } else { System.out.println("失敗"); } System.out.print("當前樹的前序遍歷為: "); binaryTree.prefixList(); System.out.println("\n====================="); } /** * 前序遍歷 */ public void prefixList() { // 判斷根節點是否存在 if (root == null) { System.out.println("當前樹為 空樹"); return; } // 存在根節點,則進行前序遍歷 root.prefixList(); } /** * 前序查找 */ public TreeNode<K> prefixSearch(K data) { // 判斷根節點是否存在 if (root == null) { return null; } // 存在根節點,則進行前序遍歷 return root.prefixSearch(data); } /** * 中序遍歷 */ public void infixList() { // 判斷根節點是否存在 if (root == null) { System.out.println("當前樹為 空樹"); return; } // 存在根節點,則進行中序遍歷 root.infixList(); } /** * 後序遍歷 */ public void suffixList() { // 判斷根節點是否存在 if (root == null) { System.out.println("當前樹為 空樹"); return; } // 存在根節點,則進行後序遍歷 root.suffixList(); } /** * 刪除節點,刪除失敗返回 -1,否則返回 1 * @param data 待刪除節點 * @return 刪除失敗返回 -1,否則返回 1 */ public int deleteNode(K data) { // 當根節點存在時,才可以進行刪除節點操作 if (root != null) { // 若恰好為 根節點,則直接將根節點置 null if (data.equals(root.data)) { root = null; return 1; } // 否則遞歸刪除 return root.deleteNode(data); } return -1; } } /** * 定義樹節點 * @param <K> */ class TreeNode<K> { K data; // 保存節點數據 TreeNode<K> left; // 保存節點的 左子節點 TreeNode<K> right; // 保存節點的 右子節點 public TreeNode(K data) { this.data = data; } @Override public String toString() { return "TreeNode{ data= " + data + "}"; } /** * 前序遍歷 */ public void prefixList() { // 輸出當前節點 System.out.print(this + " "); // 若左子樹不為空,則遞歸前序遍歷 左子樹 if (this.left != null) { this.left.prefixList(); } // 若右子樹不為空,則遞歸前序遍歷 右子樹 if (this.right != null) { this.right.prefixList(); } } /** * 前序查找 * @param data 待查找數據 * @return 查找失敗返回 null,查找成功返回相應的數據 */ public TreeNode<K> prefixSearch(K data) { // 若當前節點即為待查找節點,則直接返回 if (data.equals(this.data)) { return this; } TreeNode<K> result = null; // 用於保存查找節點 // 如果左子樹不為空,則遞歸前序查找 左子樹 if (this.left != null) { result = this.left.prefixSearch(data); } // 若左子樹查找成功,則返回 if (result != null) { return result; } // 如果右子樹不為空,則遞歸前序查找 右子樹 if (this.right != null) { result = this.right.prefixSearch(data); } return result; } /** * 中序遍歷 */ public void infixList() { // 若左子樹不為空,則遞歸中序遍歷 左子樹 if (this.left != null) { this.left.infixList(); } // 輸出當前節點 System.out.print(this + " "); // 若右子樹不為空,則遞歸中序遍歷 右子樹 if (this.right != null) { this.right.infixList(); } } /** * 後序遍歷 */ public void suffixList() { // 若左子樹不為空,則遞歸後序遍歷 左子樹 if (this.left != null) { this.left.suffixList(); } // 若右子樹不為空,則遞歸後序遍歷 右子樹 if (this.right != null) { this.right.suffixList(); } // 輸出當前節點 System.out.print(this + " "); } /** * 刪除節點,此處若為非葉子節點,直接連同其 子節點 一起刪除 * @param data 待刪除數據 * @return 刪除失敗返回 -1,否則 返回 1 */ public int deleteNode(K data) { // 如果刪除節點 恰好為 左子節點,則直接將 左子節點 置 null if (this.left != null && data.equals(this.left.data)) { this.left = null; return 1; } // 如果刪除節點 恰好為 右子節點,則直接將 右子節點 置 null if (this.right != null && data.equals(this.right.data)) { this.right = null; return 1; } int result = -1; // 若左子樹不為 null,則遞歸左子樹 查找節點並刪除 if (this.left != null) { result = this.left.deleteNode(data); if (result != -1) { return result; } } // 若右子樹不為 null,則遞歸右子樹 查找節點並刪除 if (this.right != null) { result = this.right.deleteNode(data); } return result; } } 【輸出結果:】 前序遍歷: TreeNode{ data= 0} TreeNode{ data= 1} TreeNode{ data= 3} TreeNode{ data= 4} TreeNode{ data= 2} ===================== 中序遍歷: TreeNode{ data= 3} TreeNode{ data= 1} TreeNode{ data= 4} TreeNode{ data= 0} TreeNode{ data= 2} ===================== 後序遍歷: TreeNode{ data= 3} TreeNode{ data= 4} TreeNode{ data= 1} TreeNode{ data= 2} TreeNode{ data= 0} ===================== 前序查找, 查找成功, 當前節點為: TreeNode{ data= 1} ,其左節點為: TreeNode{ data= 3} ,其右節點為: TreeNode{ data= 4} ===================== 刪除節點, 成功 當前樹的前序遍歷為: TreeNode{ data= 0} TreeNode{ data= 1} TreeNode{ data= 4} TreeNode{ data= 2} =====================
4、還原二叉樹(前序 + 中序、後序 + 中序)
(1) 還原二叉樹(數組 轉 樹)
前面通過 前序、中序、後序 遍歷 可以 得到樹的節點數據,那麼根據 前序遍歷、中序遍歷、後序遍歷 得到的數據能否反推 出 樹結構呢?
數組 轉 樹(此處 不考慮 數組中存在相同值的情況,即各個樹節點均不同):
使用 前序遍歷 + 中序遍歷 或者 後序遍歷 + 中序遍歷 的形式可以反推。
其中:
前序遍歷、後序遍歷 存在是為了 定位 根節點 所在位置。
根節點定位後,就可以將 中序遍歷 數組 分為 左、右 兩部分(形成左、右 子樹),遞歸處理即可。
使用 前序 + 後序 數組的方式 雖然可以定位 根節點,但是不知道如何 劃分 左、右子樹,從而無法正確推導出 二叉樹。
(2)思路分析、代碼實現
【前序遍歷結果 + 中序遍歷結果 還原 二叉樹:】 前序遍歷結果格式為: [{根節點}{左子樹}{右子樹}] 中序遍歷結果格式為: [{左子樹}{根節點}{右子樹}] 還原步驟: 前序結果 第一個值 必為 根節點(當前節點), 通過該節點,可以將 中序結果 劃分為 左子樹、右子樹。 通過 中序結果 劃分的左子樹的大小 可以將 前序結果 除根節點外 的值 劃分為 左子樹、右子樹。 然後將 前序、中序 劃分的 左子樹、右子樹 進行遞歸處理。 舉例: 前序遍歷結果: [0, 1, 3, 4, 2] 中序遍歷結果: [3, 1, 4, 0, 2] 第一次劃分: 前序結果:[0, 1, 3, 4, 2],中序結果:[3, 1, 4, 0, 2] 根節點為 0,將中序結果劃分為 左子樹:[3, 1, 4], 右子樹: [2] 根據中序結果 左子樹大小劃分 前序結果為 左子樹:[1, 3 ,4], 右子樹:[2] 第二次劃分: 前序結果:[1, 3, 4],中序結果:[3, 1, 4] 根節點為 1,將中序結果劃分為 左子樹:[3], 右子樹: [4] 根據中序結果 左子樹大小劃分 前序結果為 左子樹:[3], 右子樹:[4] 第三次劃分: 前序結果:[3],中序結果:[3] 根節點為 3,將中序結果劃分為 左子樹:[], 右子樹: [] 根據中序結果 左子樹大小劃分 前序結果為 左子樹:[], 右子樹:[] 第四次劃分: 前序結果、中序結果 均為空,退出。 同理依次進行處理。。。 【後序遍歷結果 + 中序遍歷結果 還原 二叉樹:】 後序遍歷結果格式為: [{左子樹}{右子樹}{根節點}] 中序遍歷結果格式為: [{左子樹}{根節點}{右子樹}] 與 前序遍歷 處理類似,只是此時根節點 位於末尾。 還原步驟: 後序結果 最後一個值 必為 根節點(當前節點), 通過該節點,可以將 中序結果 劃分為 左子樹、右子樹。 通過 中序結果 劃分的左子樹的大小 可以將 後序結果 除根節點外 的值 劃分為 左子樹、右子樹。 然後將 後序、中序 劃分的 左子樹、右子樹 進行遞歸處理。 【代碼實現:】 package com.lyh.tree; import java.util.ArrayList; import java.util.Arrays; import java.util.List; public class ArrayToBinaryTree<K> { public static void main(String[] args) { // 構建二叉樹 TreeNode6<String> root = new TreeNode6<>("0"); TreeNode6<String> treeNode = new TreeNode6<>("1"); TreeNode6<String> treeNode2 = new TreeNode6<>("2"); TreeNode6<String> treeNode3 = new TreeNode6<>("3"); TreeNode6<String> treeNode4 = new TreeNode6<>("4"); root.left = treeNode; root.right = treeNode2; treeNode.left = treeNode3; treeNode.right = treeNode4; // 設置樹 根節點 ArrayToBinaryTree<String> binaryTree = new ArrayToBinaryTree<>(); // 獲取前序遍歷結果 List<String> prefixResult = binaryTree.prefixList(root); List<String> prefixResult2 = binaryTree.prefixList2(root); System.out.println("前序遍歷結果(方式一): " + prefixResult); System.out.println("前序遍歷結果(方式二): " + prefixResult2); System.out.println("================================="); // 獲取中序遍歷結果 List<String> infixResult = binaryTree.infixList(root); System.out.println("中序遍歷結果: " + infixResult); System.out.println("================================="); // 獲取後序遍歷結果 List<String> suffixResult = binaryTree.suffixList(root); System.out.println("後序遍歷結果: " + suffixResult); System.out.println("================================="); // 使用 前序遍歷結果 + 中序遍歷結果 還原 二叉樹 TreeNode6 root2 = binaryTree.prefixAndInfixToTree(prefixResult.toArray(new String[]{}), infixResult.toArray(new String[]{})); System.out.println("還原後的二叉樹前序遍歷如下: " + binaryTree.prefixList(root2)); System.out.println("還原後的二叉樹中序遍歷如下: " + binaryTree.infixList(root2)); System.out.println("還原後的二叉樹後序遍歷如下: " + binaryTree.suffixList(root2)); System.out.println("================================="); // 使用 後序遍歷結果 + 中序遍歷結果 還原 二叉樹 TreeNode6 root3 = binaryTree.suffixAndInfixToTree(suffixResult.toArray(new String[]{}), infixResult.toArray(new String[]{})); System.out.println("還原後的二叉樹前序遍歷如下: " + binaryTree.prefixList(root3)); System.out.println("還原後的二叉樹中序遍歷如下: " + binaryTree.infixList(root3)); System.out.println("還原後的二叉樹後序遍歷如下: " + binaryTree.suffixList(root3)); System.out.println("================================="); } /** * 根據 前序遍歷結果 + 中序遍歷結果 還原 二叉樹(此處不考慮 二叉樹 節點相同值,即默認 二叉樹 節點均不相同、沒有重複元素) * @param prefixResult 前序遍歷結果 * @param infixResult 中序遍歷結果 * @return 樹的根節點 */ public TreeNode6<K> prefixAndInfixToTree(K[] prefixResult, K[] infixResult) { // 遞歸結束條件 if (prefixResult == null || infixResult == null || prefixResult.length <= 0 || infixResult.length <= 0) { return null; } // 前序遍歷結果 第一個值 肯定為 樹的根節點 TreeNode6<K> root = new TreeNode6<>(prefixResult[0]); // 查找、記錄 中序序列 中 根節點 位置 int index = 0; for (int i = 0; i < infixResult.length; i++) { if (prefixResult[0].equals(infixResult[i])) { index = i; break; } } // 根據 根節點,將 中序遍歷結果 劃分為 左子樹 以及 右子樹,中序結果 左邊即為左子樹,右邊即為 右子樹 // 中序遍歷結果:[{左子樹}{根節點}{右子樹}] K[] leftInfixResult = Arrays.copyOfRange(infixResult, 0, index); K[] rightInfixResult = Arrays.copyOfRange(infixResult, index + 1, infixResult.length); // 根據左子樹 個數,將剩餘 前序遍歷 結果劃分為 左子樹、右子樹 // 前序遍歷結果為:[{根節點}{左子樹}{右子樹}] K[] leftPrefixResult = Arrays.copyOfRange(prefixResult, 1, leftInfixResult.length + 1); K[] rightPrefixResult = Arrays.copyOfRange(prefixResult, leftInfixResult.length + 1, prefixResult.length); // 設置 根(當前)節點 左、右子樹 root.left = prefixAndInfixToTree(leftPrefixResult, leftInfixResult); root.right = prefixAndInfixToTree(rightPrefixResult, rightInfixResult); return root; } /** * 根據 後序遍歷結果 + 前序遍歷結果 還原 二叉樹 * @param suffixResult 後序遍歷結果 * @param infixResult 前序遍歷結果 * @return 樹的根節點 */ public TreeNode6<K> suffixAndInfixToTree(K[] suffixResult, K[] infixResult) { if (suffixResult == null || infixResult == null || suffixResult.length <= 0 || infixResult.length <= 0) { return null; } // 後序遍歷結果 最後一個值 肯定為 根節點(當前節點) TreeNode6<K> root = new TreeNode6<>(suffixResult[suffixResult.length - 1]); // 查找、記錄 中序序列 中 根節點 位置 int index = 0; for(int i = 0; i < infixResult.length; i++) { if (root.data.equals(infixResult[i])) { index = i; break; } } // 根據 根節點,將 中序遍歷結果 劃分為 左子樹 以及 右子樹,中序結果 左邊即為左子樹,右邊即為 右子樹 // 中序遍歷結果:[{左子樹}{根節點}{右子樹}] K[] leftInfixResult = Arrays.copyOfRange(infixResult, 0, index); K[] rightInfixResult = Arrays.copyOfRange(infixResult, index + 1, infixResult.length); // 根據左子樹 個數,將剩餘 後序遍歷 結果劃分為 左子樹、右子樹 // 後序遍歷結果為:[{左子樹}{右子樹}{根節點}] K[] leftSuffixResult = Arrays.copyOfRange(suffixResult, 0, leftInfixResult.length); K[] rightSuffixResult = Arrays.copyOfRange(suffixResult, leftInfixResult.length, suffixResult.length - 1); // 設置 根(當前)節點 左、右子樹 root.left = suffixAndInfixToTree(leftSuffixResult, leftInfixResult); root.right = suffixAndInfixToTree(rightSuffixResult, rightInfixResult); return root; } /** * 返回前序遍歷結果(方式一) * @param root 樹的根節點 * @return 前序遍歷結果 */ public List<K> prefixList(TreeNode6<K> root) { if (root == null) { System.out.println("當前為空樹"); return null; } return root.prefixList(new ArrayList<>()); } /** * 返回前序遍歷結果(方式二) * @param root 樹的根節點 * @return 前序遍歷結果 */ public List<K> prefixList2(TreeNode6<K> root) { if (root == null) { System.out.println("當前為空樹"); return null; } List<K> result = new ArrayList<>(); root.prefixList2(result); return result; } /** * 中序遍歷 * @param root 樹的根節點 * @return 中序遍歷結果 */ public List<K> infixList(TreeNode6<K> root) { if (root == null) { System.out.println("當前為空樹"); return null; } List<K> result = new ArrayList<>(); root.infixList(result); return result; } /** * 後序遍歷 * @param root 樹的根節點 * @return 後序遍歷結果 */ public List<K> suffixList(TreeNode6<K> root) { if (root == null) { System.out.println("當前為空樹"); return null; } List<K> result = new ArrayList<>(); root.suffixList(result); return result; } } /** * 定義樹節點 * @param <K> */ class TreeNode6<K> { K data; // 保存節點數據 TreeNode6<K> left; // 保存 左子節點 TreeNode6<K> right; // 保存 右子節點 public TreeNode6(K data) { this.data = data; } /** * 前序遍歷(第一種方式:帶有返回值的遍歷) * @param list 前序遍歷序列 * @return 前序遍歷結果 */ public List<K> prefixList(List<K> list) { // 用於保存當前序列,作用域只存在當前方法,返回時 作用域消失,即 遞歸時無需考慮會影響 上一次結果 List<K> result = new ArrayList<>(list); // 添加當前節點 result.add(this.data); // 遞歸添加左子節點 if (this.left != null) { result = this.left.prefixList(result); } // 遞歸添加右子節點 if (this.right != null) { result = this.right.prefixList(result); } return result; } /** * 前序遍歷(第二種方式:無返回值的遍歷) * @param result 前序遍歷序列 */ public void prefixList2(List<K> result) { // 保存當前節點 result.add(this.data); // 遞歸添加左子節點 if (this.left != null) { this.left.prefixList2(result); } // 遞歸添加右子節點 if (this.right != null) { this.right.prefixList2(result); } } /** * 中序遍歷 * @param result 中序遍歷序列 */ public void infixList(List<K> result) { // 遞歸遍歷 左子節點 if (this.left != null) { this.left.infixList(result); } // 保存當前節點 result.add(this.data); // 遞歸遍歷 右子節點 if (this.right != null) { this.right.infixList(result); } } /** * 後序遍歷 * @param result 後序遍歷序列 */ public void suffixList(List<K> result) { // 遞歸遍歷 左子節點 if (this.left != null) { this.left.suffixList(result); } // 遞歸遍歷 右子節點 if (this.right != null) { this.right.suffixList(result); } // 保存當前節點 result.add(this.data); } } 【輸出結果:】 前序遍歷結果(方式一): [0, 1, 3, 4, 2] 前序遍歷結果(方式二): [0, 1, 3, 4, 2] ================================= 中序遍歷結果: [3, 1, 4, 0, 2] ================================= 後序遍歷結果: [3, 4, 1, 2, 0] ================================= 還原後的二叉樹前序遍歷如下: [0, 1, 3, 4, 2] 還原後的二叉樹中序遍歷如下: [3, 1, 4, 0, 2] 還原後的二叉樹後序遍歷如下: [3, 4, 1, 2, 0] ================================= 還原後的二叉樹前序遍歷如下: [0, 1, 3, 4, 2] 還原後的二叉樹中序遍歷如下: [3, 1, 4, 0, 2] 還原後的二叉樹後序遍歷如下: [3, 4, 1, 2, 0] =================================
5、順序二叉樹(數組 與 樹 互轉)
(1)什麼是順序二叉樹:
是二叉樹的一種 存儲形式(按照數組順序,從上到下、從左到右 依次 給二叉樹 添加樹節點,得到一個完全二叉樹 或者 滿二叉樹),
其 可以在 數組 與 樹 之間相互轉換。即 根據一個數組,可以得到 樹 的結構,從樹也可以反推 數組。
特點:
順序二叉樹通常只考慮 完全二叉樹。
其第 n 個元素的左子節點為 2*n + 1。
其第 n 個元素的右子節點為 2*n + 2。
其第 n 個元素的父節點為 (n – 1) / 2。 (n 從 0 開始,即從數組第一個元素下標開始計數)。
(2)代碼實現:
【核心:】 對於第 n 個元素(n 從 0 開始計數): 其左子節點為 2*n + 1。 其右子節點為 2*n + 2。 無論 數組 轉 樹 還是 樹 轉 數組,都是根據這兩個 值進行對應。 註: 通過先序、中序、後序 可以遍歷樹, 那麼在遍歷的同時將節點 設置到相應的 數組下標處,那麼即可完成 樹 轉 數組。 【代碼實現:】 package com.lyh.tree; import java.util.Arrays; public class ArrayBinaryTree<K> { private K[] arrays; public ArrayBinaryTree(K[] arrays) { this.arrays = arrays; } public static void main(String[] args) { // 構建數組 Integer[] arrays = new Integer[]{1, 2, 3, 4, 5, 6, 7}; ArrayBinaryTree<Integer> arrayBinaryTree = new ArrayBinaryTree<>(arrays); // 數組轉為 樹 TreeNode2 root = arrayBinaryTree.arraysToTree(); // 輸出數組 System.out.println("數組為: " + Arrays.toString(arrays)); System.out.println("=============================="); // 輸出樹 的前序遍歷結果 System.out.print("樹 的前序遍歷為: "); root.prefixList(); System.out.println("\n=============================="); // 輸出樹 的中序遍歷結果 System.out.print("樹 的中序遍歷為: "); root.infixList(); System.out.println("\n=============================="); // 輸出樹 的後序遍歷結果 System.out.print("樹 的後序遍歷為: "); root.suffixList(); System.out.println("\n=============================="); System.out.print("樹 轉為數組為: "); Object[] result = arrayBinaryTree.treeToArray(root); System.out.println(Arrays.toString(result)); } /** * 數組 轉 樹 * @return 樹的根節點,若數組為空 則返回 null。 */ public TreeNode2<K> arraysToTree() { // 若數組為空,則不進行 轉樹 操作 if (arrays == null || arrays.length == 0) { System.out.println("數據為空,無法轉為樹"); return null; } // 設置根節點 TreeNode2 root = new TreeNode2(arrays[0]); // 根據數組值 構建樹 root.arrayToTree(arrays, 0); return root; } public Object[] treeToArray(TreeNode2<K> root) { // 判斷樹 是否為空樹 if (root == null) { System.out.println("數據為空,無法轉為數組"); return null; } // 樹非空,計算樹節點個數 int length = root.size() + 1; // 聲明一個數組 Object[] arrays = new Object[length]; // 將樹的數據 放入 數組對應 下標處 root.treeToArray(arrays, 0); return arrays; } } /** * 定義樹節點 * @param <K> */ class TreeNode2<K> { K data; // 保存節點數據 TreeNode2<K> left; // 保存節點的 左子節點 TreeNode2<K> right; // 保存節點的 右子節點 public TreeNode2(K data) { this.data = data; } @Override public String toString() { return "TreeNode2{ data = " + data + " }"; } /** * 數組 轉 樹 * @param arrays 待轉換數組 * @param index 當前數組下標(從 0 開始,表示數組第一個元素,同樣表示為 根節點) */ public void arrayToTree(K[] arrays, int index) { // 若當前節點存在 左節點,則遞歸構建 左子樹 if (index * 2 + 1 < arrays.length) { this.left = new TreeNode2<>(arrays[index * 2 + 1]); this.left.arrayToTree(arrays, index * 2 + 1); } // 若當前節點存在 右節點,則遞歸構建 右子樹 if (index * 2 + 2 < arrays.length) { this.right = new TreeNode2<>(arrays[index * 2 + 2]); this.right.arrayToTree(arrays, index * 2 + 2); } } /** * 二叉樹 轉 數組(先序遍歷實現) * @param arrays 待轉換數組 * @param index 數組下標 */ public void treeToArray(Object[] arrays, int index) { // 設置當前節點 到相應的數組下標處 arrays[index] = this.data; // 遍歷左子樹 if (this.left != null) { this.left.treeToArray(arrays, index * 2 + 1); } // 遍歷右子樹 if (this.right != null) { this.right.treeToArray(arrays, index * 2 + 2); } } /** * 前序遍歷 */ public void prefixList() { // 輸出當前節點 System.out.print(this + " "); // 若左子樹不為空,則遞歸前序遍歷 左子樹 if (this.left != null) { this.left.prefixList(); } // 若右子樹不為空,則遞歸前序遍歷 右子樹 if (this.right != null) { this.right.prefixList(); } } /** * 中序遍歷 */ public void infixList() { // 若左子樹不為空,則遞歸中序遍歷 左子樹 if (this.left != null) { this.left.infixList(); } // 輸出當前節點 System.out.print(this + " "); // 若右子樹不為空,則遞歸中序遍歷 右子樹 if (this.right != null) { this.right.infixList(); } } /** * 後序遍歷 */ public void suffixList() { // 若左子樹不為空,則遞歸後序遍歷 左子樹 if (this.left != null) { this.left.suffixList(); } // 若右子樹不為空,則遞歸後序遍歷 右子樹 if (this.right != null) { this.right.suffixList(); } // 輸出當前節點 System.out.print(this + " "); } /** * 求樹節點總數 * @return 樹節點總數 */ public int size() { int left = 0; // 左節點個數 int right = 0; // 右節點個數 // 遞歸求左節點個數 if (this.left != null) { left = 1 + this.left.size(); } // 遞歸求右節點個數 if (this.right != null) { right = 1 + this.right.size(); } // 返回總個數 return left + right; } } 【輸出結果:】 數組為: [1, 2, 3, 4, 5, 6, 7] ============================== 樹 的前序遍歷為: TreeNode2{ data = 1 } TreeNode2{ data = 2 } TreeNode2{ data = 4 } TreeNode2{ data = 5 } TreeNode2{ data = 3 } TreeNode2{ data = 6 } TreeNode2{ data = 7 } ============================== 樹 的中序遍歷為: TreeNode2{ data = 4 } TreeNode2{ data = 2 } TreeNode2{ data = 5 } TreeNode2{ data = 1 } TreeNode2{ data = 6 } TreeNode2{ data = 3 } TreeNode2{ data = 7 } ============================== 樹 的後序遍歷為: TreeNode2{ data = 4 } TreeNode2{ data = 5 } TreeNode2{ data = 2 } TreeNode2{ data = 6 } TreeNode2{ data = 7 } TreeNode2{ data = 3 } TreeNode2{ data = 1 } ============================== 樹 轉為數組為: [1, 2, 3, 4, 5, 6, 7]
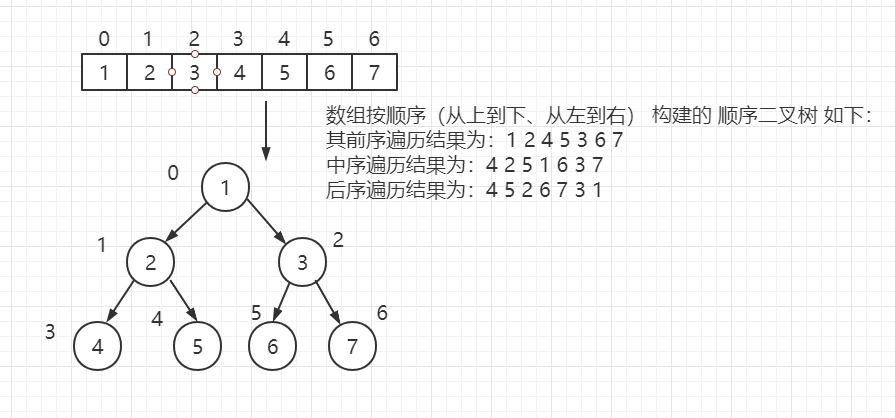
6、線索二叉樹
(1)什麼是線索二叉樹?
對於 n 個節點的 二叉樹,其總共含有 2*n – (n – 1) = n + 1 個空的指針域。
利用這些空的指針域,存放 當前節點 在 某次遍歷(前序、中序、後續)下的 前驅、後繼 節點的指針。
這些指向 前驅、後繼 節點的指針稱為 線索,使用這種線索的二叉樹 稱為線索二叉樹。
即 線索二叉樹的本質 是 將二叉樹 當前節點的空閑指針 改為 指向當前節點 前驅 或者 後繼 節點的過程。
而根據遍歷的分類,前驅、後繼節點會不同,可以分為:
前序線索二叉樹、中序線索二叉樹、後序線索二叉樹。
(2)代碼實現 中序線索二叉樹
【定義樹節點:】 對於每個節點的 左、右指針域 來說,可能是 空閑指針域,也可能指向 左、右 子節點。 需要對其進行區分,可以定義指針類型,比如:leftType,值為 0 時表示指向子節點, 值為 1 時表示為 空閑指針域(存儲線索 -- 前驅、後繼節點) 樹節點: class TreeNode3<K> { K data; // 保存節點數據 TreeNode3<K> left; // 保存左子節點 TreeNode3<K> right; // 保存右子節點 byte leftType; // 值為 0 時表示為 左子節點,值為 1 時表示存儲線索 -- 前驅節點 byte rightType; // 值為 0 時表示為 右子節點,值為 1 時表示存儲線索 -- 後繼節點 public TreeNode3(K data) { this.data = data; } @Override public String toString() { return "TreeNode3{ data= " + data + " }"; } } 【構建線索二叉樹(以 中序遍歷 構建 線索二叉樹 為例):】 首先得構建一個 二叉樹,可以使用 順序二叉樹(詳見上例,數組 轉 二叉樹) 或者 手動構建。 中序遍歷二叉樹時,無法直接 明確 當前節點的 前驅、後繼 節點。 可以使用變量 preNode 用於記錄 當前節點的前驅節點。 若 當前節點 node 的左指針域 left 為 null,則將其 指向 前驅節點 preNode,並修改指針類型為 線索。 若 前驅節點 preNode 的右指針域 right 為 null,則將其 指向 當前節點 node,並修改指針類型為 線索。 在進入下一個 節點前,需要使用 前驅節點 保存 當前節點。 註: 此處使用變量記錄 前驅節點 即可,當然使用 另一個變量 nextNode 記錄 後繼節點亦可實現。 即: // 設置前驅節點 if (node.left == null) { node.left = preNode; // 指向 當前節點 的前驅節點 node.leftType = 1; // 修改左指針域 指針類型為 線索 } // 設置後繼節點 if (preNode != null && preNode.right == null) { preNode.right = node; preNode.rightType = 1; // 修改右指針域 指針類型為 線索 } // 進入下一個節點前,保存當前節點,作為前驅節點 preNode = node; 【遍歷 線索二叉樹(使用中序遍歷 並根據 後繼節點 的方式輸出 中序線索二叉樹):】 由於 樹節點 的 左、右指針 並不一定為空(存放了 前驅、後繼 節點),原始的二叉樹 前序、中序、後序遍歷 方式已不適用。 但是一般通過其 前驅節點 或者 後繼節點 查找。 以後繼節點為例: 與 原始遍歷 相同,按照 左子節點、當前節點、右子節點 的順序 訪問。 訪問左子樹,若 當前節點 左子節點為 線索(指向 前驅節點),則輸出 當前節點,若不是,則按照 中序遍歷 方式進行遍歷。 訪問右子樹,若 當前節點 右子節點為 線索(指向 後繼節點),則輸出 後繼節點,若不是,則按照 中序遍歷 方式進行遍歷。 即: // 從 根節點 開始遍歷(中序方式) while(node != null) { // 遍歷左指針域, leftType = 0 時為左子樹,依次往下遍歷,直至 leftType = 1。表示當前節點的左指針域 線索化(即當前節點為有效節點) while(node.leftType == 0) { node = node.left; } // 操作當前節點 System.out.print(node + " "); // 遍歷右指針域,若當前節點的 右指針域 線索化,則輸出當前節點的 後繼節點 while(node.rightType == 1) { node = node.right; System.out.print(node + " "); } // 當前節點 右指針域 非線索化,則替換當前節點,開始下一次循環 node = node.right; } 前驅節點方式: 與後繼節點相反處理,按照 右子節點、當前節點、左子節點 的順序訪問。 最後返回的是 樹的 逆序中序遍歷 的順序。 【代碼實現:】 package com.lyh.tree; import java.util.Arrays; /** * 線索二叉樹 * @param <K> */ public class ThreadBinaryTree<K> { private TreeNode3<K> preNode; // 用於記錄當前節點的上一個節點 public static void main(String[] args) { // 將數組 轉為 順序二叉樹 Integer[] arrays = new Integer[]{1, 2, 3, 4, 5}; ThreadBinaryTree<Integer> threadBinaryTree = new ThreadBinaryTree<>(); TreeNode3<Integer> root = threadBinaryTree.arrayToTree(arrays, 0); // 使用 中序遍歷 遍歷 順序二叉樹,並添加線索,使其成為 中序線索二叉樹 threadBinaryTree.infixCreateThreadBinaryTree(root); // 中序遍歷 以 後繼節點 的方式 輸出 中序線索二叉樹 System.out.println("原數組為: " + Arrays.toString(arrays)); System.out.println("數組 ==> 轉為中序線索二叉樹(後繼節點方式) 輸出為: "); threadBinaryTree.infixNextNodeList(root); System.out.println("\n數組 ==> 轉為中序線索二叉樹(前驅節點方式) 輸出為: "); threadBinaryTree.infixPreNodeList(root); } /** * 根據數組構建一個 順序二叉樹 * @param arrays 數組 * @param index 數組下標 * @return 順序二叉樹 */ public TreeNode3<K> arrayToTree(K[] arrays, int index) { TreeNode3<K> root = null; // 設置根節點 // 遞歸數組並將對應的值存入 順序二叉樹 if (index >= 0 && index < arrays.length) { // 設置當前節點 root = new TreeNode3<>(arrays[index]); // 設置當前節點左子節點 root.left = arrayToTree(arrays, index * 2 + 1); // 設置當前節點右子節點 root.right = arrayToTree(arrays, index * 2 + 2); } return root; } /** * 中序遍歷並創建線索化二叉樹 * @param node 樹節點 */ public void infixCreateThreadBinaryTree(TreeNode3<K> node) { // 判斷當前節點是否為空,即 葉子節點 或者 空樹 if (node == null) { return; } // 遍歷左子節點 infixCreateThreadBinaryTree(node.left); // 操作當前節點 // 設置前驅節點 if (node.left == null) { node.left = preNode; // 指向 當前節點 的前驅節點 node.leftType = 1; // 修改左指針域 指針類型為 線索 } // 設置後繼節點 if (preNode != null && preNode.right == null) { preNode.right = node; preNode.rightType = 1; // 修改右指針域 指針類型為 線索 } // 進入下一個節點前,保存當前節點,作為前驅節點 preNode = node; // 遍歷右子節點 infixCreateThreadBinaryTree(node.right); } /** * 以中序遍歷方式 並根據 後繼節點 輸出 中序線索二叉樹 * @param node 根節點 */ public void infixNextNodeList(TreeNode3<K> node) { // 從 根節點 開始遍歷(中序方式) while(node != null) { // 遍歷左指針域, leftType = 0 時為左子樹,依次往下遍歷,直至 leftType = 1。表示當前節點的左指針域 線索化(即當前節點為有效節點) while(node.leftType == 0) { node = node.left; } // 操作當前節點 System.out.print(node + " "); // 遍歷右指針域,若當前節點的 右指針域 線索化,則輸出當前節點的 後繼節點 while(node.rightType == 1) { node = node.right; System.out.print(node + " "); } // 當前節點 右指針域 非線索化,則替換當前節點,開始下一次循環 node = node.right; } } /** * 以中序遍歷方式 並根據 前驅節點 反向輸出 中序線索二叉樹 * @param node 根節點 */ public void infixPreNodeList(TreeNode3 node) { // 從根節點開始遍歷 while(node != null) { // 遍歷右指針域,找到線索化 節點 while(node.right != null && node.rightType == 0) { node = node.right; } // 操作當前節點 System.out.print(node + " "); // 遍歷左指針域,若當前左指針域 線索化,則輸出當前節點的 前驅節點 while(node.left != null && node.leftType == 1) { node = node.left; System.out.print(node + " "); } // 當前節點 左指針域 非線索化,則替換當前節點,開始下一次循環 node = node.left; } } } /** * 定義樹節點 * @param <K> */ class TreeNode3<K> { K data; // 保存節點數據 TreeNode3<K> left; // 保存左子節點 TreeNode3<K> right; // 保存右子節點 byte leftType; // 值為 0 時表示為 左子節點,值為 1 時表示存儲線索 -- 前驅節點 byte rightType; // 值為 0 時表示為 右子節點,值為 1 時表示存儲線索 -- 後繼節點 public TreeNode3(K data) { this.data = data; } @Override public String toString() { return "TreeNode3{ data= " + data + " }"; } } 【輸出結果:】 原數組為: [1, 2, 3, 4, 5] 數組 ==> 轉為中序線索二叉樹(後繼節點方式) 輸出為: TreeNode3{ data= 4 } TreeNode3{ data= 2 } TreeNode3{ data= 5 } TreeNode3{ data= 1 } TreeNode3{ data= 3 } 數組 ==> 轉為中序線索二叉樹(前驅節點方式) 輸出為: TreeNode3{ data= 3 } TreeNode3{ data= 1 } TreeNode3{ data= 5 } TreeNode3{ data= 2 } TreeNode3{ data= 4 }
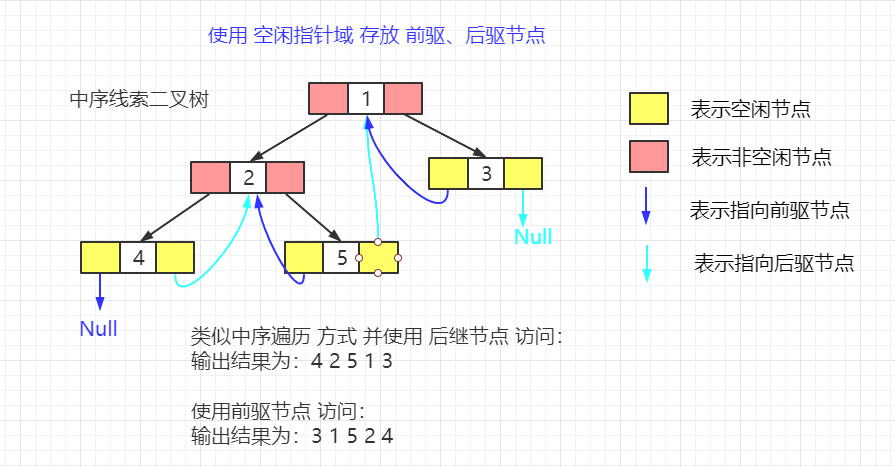
7、哈夫曼樹(HuffmanTree、最優二叉樹)
(1)什麼是哈夫曼樹?
哈夫曼樹 又稱 最優二叉樹。對於 n 個節點 且 每個節點有一個值(權值),將這 n 個節點構建成一個 二叉樹,使得該樹的 帶權路徑長度(weighted path length,簡稱 wpl)最小。這樣的二叉樹 稱為 最優二叉樹(或者 哈夫曼樹)。
註:
哈夫曼樹構建完成後,n 個節點 均為 哈夫曼樹 的葉子節點。
【基本關鍵詞概念:】
路徑 與 路徑長度:
在一棵樹中,一個節點 到達 另一個節點 之間的 分支通路 稱為 路徑。
通路中 分支的總數 稱為 路徑長度。
節點的權:
簡單的理解為 節點中帶有某含義的值。
節點的帶權路徑長度:
從根節點 到 該節點之間的路徑長度 與 該節點的 權的乘積。
樹的帶權路徑長度:
該樹所有的 葉子節點 的帶權路徑長度 之和。
哈夫曼樹(最優二叉樹):
樹的帶權路徑(wpl)最小的二叉樹 為 哈夫曼樹。
一般權值越大的節點 離 根節點 越近 的二叉樹才是最優二叉樹。
wpl 相同的二叉樹 其 哈夫曼樹可能不同。
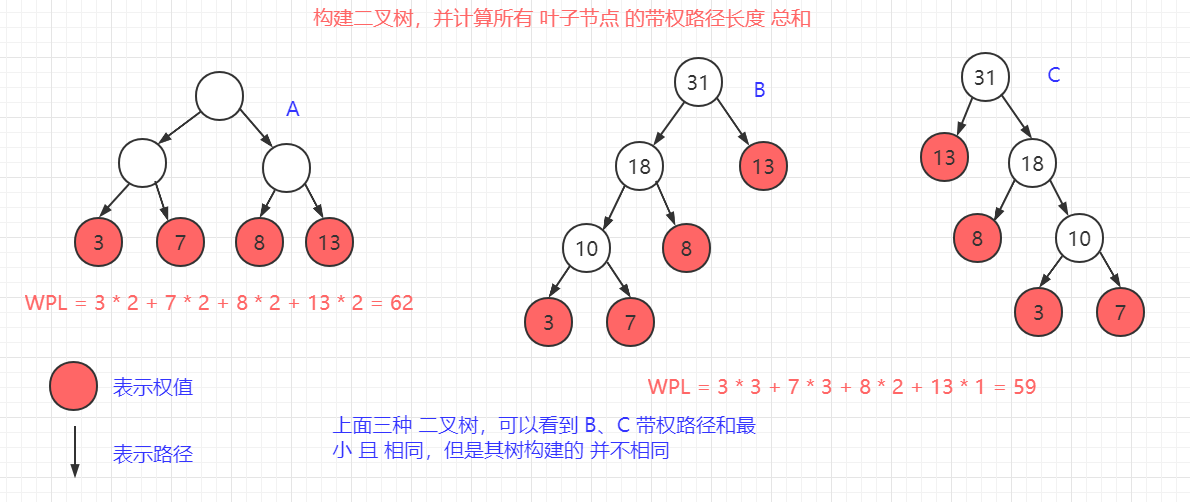
(2)創建 哈夫曼樹
【哈夫曼樹創建步驟:】 Step1:對於一組數據,先將數據 按照 權值 從小到大 排序。 Step2:將數據中每一個值 視為一個樹節點(最簡單的二叉樹), Step2.1:從數據中選取 權值 最小的兩個值 作為 左、右子節點 並構建一個新的二叉樹。 Step2.2:新的二叉樹 權值為 左、右子節點 權值之和。 Step2.3:刪除已被選擇的左、右節點,並將新的節點 加入 數據中(按照權值從小到大排序)。 Step3:重複 Step2 操作,直至數據中只剩 一個值,即 哈夫曼樹的 根節點。 註: 一般來說 權值最大 的葉子節點 離 根節點越近的 二叉樹為 最優二叉樹。 所以每次拼接時,均選取當前節點中 最小權值的兩個節點進行拼接,將最大權值的節點留在最後拼接。 【代碼實現:】 package com.lyh.tree; import java.util.ArrayList; import java.util.Arrays; import java.util.Collections; import java.util.List; /** * 哈夫曼樹 */ public class HuffmanTree<K> { public static void main(String[] args) { // 根據數組構建哈夫曼樹(此處構建規則為 左子節點權值 小於 右子節點) int[] arrays = new int[]{8, 3, 7, 13}; HuffmanTree<String> huffmanTree = new HuffmanTree<>(); TreeNode4 root = huffmanTree.createHuffmanTree(arrays); // 輸出哈夫曼樹前序遍歷 System.out.print("哈夫曼樹前序遍歷為: "); root.prefixList(); } /** * 構建哈夫曼樹,返回樹的根節點 * @param arrays 待構建樹的數組(節點 權值 組成的數組) * @return 哈夫曼樹根節點 */ public TreeNode4<K> createHuffmanTree(int[] arrays) { // 構建樹節點,此處借用 集合,並利用集合進行排序操作 List<TreeNode4<K>> lists = new ArrayList<>(); Arrays.stream(arrays).forEach( x -> { lists.add(new TreeNode4<>(x)); }); // 遍歷構建哈夫曼樹,此處規則為 左子節點權值 小於 右子節點權值 while (lists.size() > 1) { // 節點按權值 從小到大排序 Collections.sort(lists); // 獲取左子節點 TreeNode4<K> leftNode = lists.get(0); // 獲取右子節點 TreeNode4<K> rightNode = lists.get(1); // 組合成 二叉樹 TreeNode4<K> parentNode = new TreeNode4<>(leftNode.value + rightNode.value); parentNode.left = leftNode; parentNode.right = rightNode; // 從集合中移除已使用節點,並將新節點添加到集合中 lists.remove(leftNode); lists.remove(rightNode); lists.add(parentNode); } // 集合中最後元素即為 哈夫曼樹 根節點 return lists.get(0); } } /** * 定義樹節點 * @param <K> */ class TreeNode4<K> implements Comparable<TreeNode4<K>>{ K data; // 保存節點值 int value; // 保存節點權值 TreeNode4<K> left; // 保存左子節點 TreeNode4<K> right; // 保存右子節點 public TreeNode4(int value) { this.value = value; } @Override public String toString() { return "TreeNode4{ value = " + value + " }"; } @Override public int compareTo(TreeNode4<K> o) { return this.value - o.value; } /** * 前序遍歷 */ public void prefixList() { // 輸出當前節點 System.out.print(this + " "); // 遍歷左子節點 if (this.left != null) { this.left.prefixList(); } // 遍歷右子節點 if (this.right != null) { this.right.prefixList(); } } } 【輸出結果:】 哈夫曼樹前序遍歷為: TreeNode4{ value = 31 } TreeNode4{ value = 13 } TreeNode4{ value = 18 } TreeNode4{ value = 8 } TreeNode4{ value = 10 } TreeNode4{ value = 3 } TreeNode4{ value = 7 }
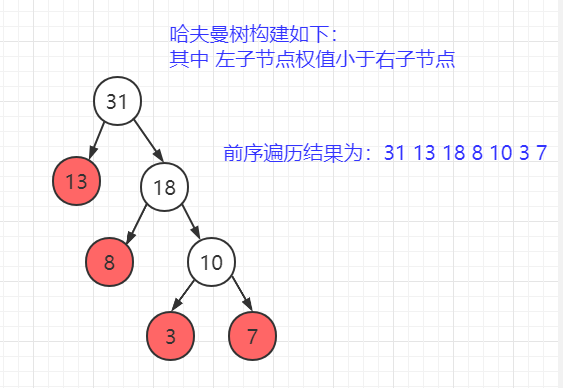
8、哈夫曼編碼 實現 文件壓縮、解壓
(1)什麼是 哈夫曼編碼?
哈夫曼編碼 是一種 可變字長編碼,可用於數據壓縮、節省存儲空間。
將文件轉為 位元組數組,並根據 各位元組 出現頻率為權值,構建哈夫曼樹,並得到每個位元組的 哈夫曼編碼(出現頻率越高的位元組 其編碼 越短,從而達到縮減存儲空間的目的),再根據 哈夫曼編碼將 位元組轉換為對應的 二進制 串,最後以 8 位為單位 壓縮二進制串 成 位元組數組,即可實現 文件的壓縮。
(2)補充點 二進制 與 整數 相互轉換的概念
【Java 中二進制 與 整數 互相轉換:】 String 轉 int: int parseInt(String s, int radix); 其中: s 表示 二進制字符串, radix 表示進制, 即 按照 幾進制 去 處理 二進制字符串。 int 轉 String: String toBinaryString(int i); 其中: i 表示待轉換的整數。 註: 若結果為非負數,輸出結果 前面的 0 會省略(處理時需要額外注意)。 比如: 5 可以為 101、0101、00101,,但是最終輸出結果為 101. int 轉 byte(強轉): byte (byte)parseInt(String s, int radix) 【Java 中整數以 二進制 補碼形式存儲:】 Java 中整數使用 二進制 補碼 的形式存儲, 正數的 補碼、反碼、原碼 均相同。 負數的 補碼為 反碼 加 1。 反碼為 符號位不變,其餘各位取反。 比如: "10000101" 轉為 int 型整數時, 即 Integer.parseInt("10000101", 2); 由於 "1000 0101" 轉為 int,而 int 為 4 位元組,即為 "0000 0000 0000 0000 0000 0000 1000 0101", 其符號位為 0,即整數,補碼與原碼相同,即最終顯示為整數 133. "10000101" 轉為 byte 型整數時,即 (byte)Integer.parseInt("10000101", 2); 由於 "10000101" 轉為 byte,而 byte 為 1 位元組,即為 "10000101", 其符號位為 1,表示負數,其反碼為符號位不變,各位取反,即 "11111010"。 而 補碼為其反碼 加 1,即最終為 "11111011",即最終顯示為整數 -123. 註: byte 範圍為 -128 ~ 127,即 10000000 ~ 01111111。符號位不做計算。 【壓縮處理最後一個位元組可能遇到的問題:】 以 8 位為單位 將 二進制串 轉為 位元組(整數)數組 的時候,若 最後一個二進制串 不足 8 位,需要額外注意: 若不足 8 位直接存儲為 位元組,則解碼時 可能會出錯。 比如: (byte)Integer.parseInt("0101", 2); 轉為 byte 時其值為 5. (byte)Integer.parseInt("00101", 2); 轉為 byte 時其值也為 5. 若直接存儲,那麼解碼時, Integer.toBinaryString(5); 輸出為 101, 由於轉換的是非負數,其前面的 0 會省略。並不知道其前面到底有 幾個 0,從而解碼失敗。 我的解決方法是: 額外增加一個位元組用於記錄 最後一個 二進制串 的實際位數。 若 最後一個二進制串 轉換為 byte 整數時 為 負數,則其符號位肯定為 1,肯定滿足 8 位,此時記錄 有效位數為 8 位。 若 最後一個二進制串 轉換為 非負數,則其 解碼時 前面的 0 會省略,此時先將其 高位補 0,然後根據最後一個 位元組記錄的 有效位數 去截取即可。 比如: 0101 轉為 byte 整數 5,則額外增加一個位元組整數 4,表示有效位數為 4 位。 00101 轉為 byte 整數 5,則額外增加一個位元組整數 5,表示有效位數為 5 位。 10000101 轉為 byte 整數 -123,則額外增加要給位元組整數 8,表示有效位數為 8 位。 註: 由於 0 會被省略,所以需要對 非負數 進行 高位補位,即 0101 需要變為 00000101。 可以與 256 進行 按位與運算,即 5 | 256 = 0101 | 100000000 = 100000101, 此時截取 後 8 位二進制串即為 補位成功的 二進制串。 此時,對於 0101,其有效位數為 4 位,即截取 後四位 二進制串。 對於 00101,其有效位數為 5 位,即截取 後五為 二進制串。
(3)哈夫曼如何 壓縮、解壓
【壓縮文件的流程:】 Step1:讀取文件,根據文件中 位元組(字符) 出現的頻率 作為權值,構建出 哈夫曼樹。 將 位元組 頻率按 從小到大 排序,並構建 哈夫曼樹。 Step2:通過 哈夫曼樹,可以得到每個 位元組 的唯一編碼。 將指向左子節點分支命名為 0,指向右子節點分支命名為 1, 則從根節點 到 某個節點的路徑 記為 該節點的 編碼(比如:00,010,001 等)。 Step3:使用編碼 去替換掉 位元組。 將文件中所有的 位元組 替換成 二進制編碼。 Step4:將 8 位二進制 作為一個位元組 進行轉碼,轉成位元組數組 進行存儲, 最後一個 二進制串 不足 8 位時按 8 位處理,並額外增加一個位元組用於記錄其實際位數。 Step5:將 位元組數組 以及 編碼表 同時 輸出到文件中(完成壓縮)。 【解壓文件的流程:】 Step1:讀取文件中的 位元組數組 以及 編碼表。 Step2:將 位元組數組 轉為對應 的二進制串。 Step3:根據編碼表 得到解碼錶,並根據 解碼錶 將 二進制串 轉為字符。 Step4:輸出到文件即可。

(3)代碼實現
【代碼實現:】 package com.lyh.tree; import java.io.*; import java.util.*; public class HuffmanCode { private Map<Byte, String> huffmanCodes = new HashMap<>(); // 用於保存 編碼集,位元組為 key,編碼為 value private Map<String, Byte> huffmanDeCodes = new HashMap<>(); // 用於保存 解碼集,位元組為 value,編碼為 key public static void main(String[] args) { // 測試 普通字符串 test(); // 測試讀取、壓縮文件 // String srcFile = "G:/1.pdf"; // String zipFile = "G:/zip.pdf"; // String unzipFile = "G:/unzip.pdf"; // testZipFile(srcFile, zipFile); // testUnzipFile(zipFile, unzipFile); } /** * 測試文件 壓縮 */ public static void testZipFile(String srcFile, String zipFile) { FileInputStream fis = null; OutputStream os = null; ObjectOutputStream oos = null; try { // 讀取文件,將文件轉為 對應的位元組數組 fis = new FileInputStream(srcFile); byte[] b = new byte[fis.available()]; fis.read(b); // 根據 位元組數組 生成 哈夫曼樹 以及 哈夫曼編碼,根據 哈夫曼編碼將 原位元組數組 壓縮 成新的位元組數組 HuffmanCode huffmanCode = new HuffmanCode(); byte[] zipResult = huffmanCode.zipFile(b); // 輸出文件,將 位元組數組 輸出到文件中,以對象的形式存儲 數據,方便讀取。 os = new FileOutputStream(zipFile); oos = new ObjectOutputStream(os); // 記錄壓縮後的位元組數組 oos.writeObject(zipResult); // 記錄編碼集 oos.writeObject(huffmanCode.huffmanCodes); } catch (Exception e) { System.out.println("文件操作異常"); } finally { try { fis.close(); oos.close(); os.close(); } catch (IOException e) { System.out.println("文件關閉失敗"); } } } /** * 測試文件 解壓 */ public static void testUnzipFile(String srcFile, String unzipFile) { InputStream is = null; ObjectInputStream ois = null; FileOutputStream fos = null; try { // 讀取文件,將文件轉為 對應的 位元組數組 以及 哈夫曼編碼 is = new FileInputStream(srcFile); ois = new ObjectInputStream(is); // 讀取 位元組數組 byte[] b = (byte[])ois.readObject(); // 讀取 編碼集 Map<Byte, String> codes = (Map<Byte, String>) ois.readObject(); // 根據 編碼集 將 位元組數組 解碼,得到解壓後的數組 HuffmanCode huffmanCode = new HuffmanCode(); huffmanCode.huffmanCodes = codes; byte[] unzipResult = huffmanCode.deCompressAndConvert(b); // 將解壓後的數組寫入文件 fos = new FileOutputStream(unzipFile); fos.write(unzipResult); } catch (Exception e) { System.out.println("文件操作異常"); } finally { try { ois.close(); is.close(); fos.close(); } catch (Exception e) { System.out.println("文件"); } } } /** * 測試 壓縮、解壓 普通字符串 * Step1:讀取 普通字符串 轉為位元組數組, * Step2:根據位元組數組 構建 哈夫曼樹, * Step3: 根據 哈夫曼樹 得到 所有葉子節點的 編碼,組成編碼集。 */ public static void test() { // 將字符轉為 位元組數組,並生成對應的 哈夫曼樹 HuffmanCode huffmanCode = new HuffmanCode(); String data = "Java C++"; TreeNode5 root = huffmanCode.createHuffman(data.getBytes()); System.out.println("當前字符串為: " + data); System.out.println("轉為位元組數組為: " + Arrays.toString(data.getBytes())); // 前序遍歷輸出 哈夫曼樹 System.out.println("位元組數組轉哈夫曼樹後,前序遍歷輸出哈夫曼樹: "); root.prefixList(); System.out.println("\n==============================="); // 根據 哈夫曼樹,生成 位元組對應的 編碼表 huffmanCode.getCodes(root); System.out.println("輸出當前哈夫曼樹 葉子節點 對應的編碼表: "); huffmanCode.hufumanCodesList(); System.out.println("\n==============================="); // 根據編碼集,將 字符串對應的位元組數組 轉為 二進制,並以 8 位為單位 進一步轉為 位元組數組存儲 System.out.println("壓縮前的位元組數組為: " + Arrays.toString(data.getBytes())); byte[] result = huffmanCode.convertAndCompress(data.getBytes()); System.out.println("壓縮後的位元組數組為: " + Arrays.toString(result)); System.out.println("\n==============================="); // 解壓位元組數組 byte[] newReult = huffmanCode.deCompressAndConvert(result); System.out.println("解壓後的位元組數組為: " + Arrays.toString(newReult)); System.out.println("解壓後的字符串為:" + new String(newReult)); } /** * 壓縮文件 * @param arrays 待壓縮位元組數組 * @return 壓縮後的位元組數組 */ public byte[] zipFile(byte[] arrays) { // 根據位元組數組 位元組出現頻率 構建 哈夫曼樹,根據 哈夫曼樹 生成對應的 哈夫曼編碼 getCodes(createHuffman(arrays)); // 根據 哈夫曼編碼 將位元組數組 對應的位元組 轉為 二進制串,二進制串 以 8 位為單位再轉為 位元組數組存儲 return convertAndCompress(arrays); } /** * 解壓文件 * @param arrays 待解壓位元組數組 * @return 解壓後的位元組數組 */ public byte[] unzipFile(byte[] arrays) { return deCompressAndConvert(arrays); } /** * 構建哈夫曼樹 * @param arrays 位元組數組 * @return 哈夫曼樹根節點 */ public TreeNode5 createHuffman(byte[] arrays) { // 遍歷位元組數組,記錄 每個位元組 出現的頻率作為 權值,使用 哈希表,key 存位元組,value 存位元組出現頻率 Map<Byte, Long> map = new HashMap<>(); for (byte temp : arrays) { map.put(temp, map.getOrDefault(temp, 0L) + 1); } // 根據 權值 創建樹節點 List<TreeNode5> lists = new ArrayList<>(); for (Map.Entry<Byte, Long> temp : map.entrySet()) { lists.add(new TreeNode5(temp.getKey(), temp.getValue())); } // Collections.sort(lists); // System.out.println("權值集合為: " + lists); // System.out.println("==============================="); // 遍歷構建 哈夫曼樹 while(lists.size() > 1) { // 排序,從小到大排序(即 哈夫曼樹 左子節點權值 小於 右子節點) Collections.sort(lists); // 獲取左子節點 TreeNode5 leftNode = lists.get(0); // 獲取右子節點 TreeNode5 rightNode = lists.get(1); // 創建二叉樹(此處非葉子節點 值為 null,只含有權值) TreeNode5 parentNode = new TreeNode5(null, leftNode.value + rightNode.value); parentNode.left = leftNode; parentNode.right = rightNode; // 移除已使用節點,添加新節點 lists.remove(leftNode); lists.remove(rightNode); lists.add(parentNode); } // 返回哈夫曼樹根節點 return lists.get(0); } /** * 獲取 哈夫曼樹 所有 葉子節點 的路徑,即 編碼字符串。 * 規定:左分支為 0,右分支 為 1. * @param node 哈夫曼樹根節點 */ public void getCodes(TreeNode5 node, String code, StringBuilder stringBuilder) { // 構建一個新的 StringBuilder 用於拼接字符串,當某次遞歸方法調用結束後,此變量作用域會消失,即不會影響之前的 StringBuilder StringBuilder stringBuilder2 = new StringBuilder(stringBuilder); stringBuilder2.append(code); // 判斷當前節點是否為 空 if (node != null) { // 若當前節點值不為 null,即為 葉子節點 if (node.data != null) { // 保存到 編碼集 中 huffmanCodes.put(node.data, stringBuilder2.toString()); } else { // 遞歸遍歷左子樹(左子節點),左分支為 0 getCodes(node.left, "0", stringBuilder2); // 遞歸遍歷右子樹(右子節點),右分支為 1 getCodes(node.right, "1", stringBuilder2); } } } /** * 重載 獲取 編碼集方法,根據 根節點 遍歷 哈夫曼樹 * @param root 哈夫曼樹根節點 */ public void getCodes(TreeNode5 root) { getCodes(root, "", new StringBuilder()); } /** * 根據 編碼集 得到 解碼集 * @param huffmanCodes 解碼集 */ public void getDeCodes(Map<Byte, String> huffmanCodes) { for (Map.Entry<Byte, String> temp : huffmanCodes.entrySet()) { huffmanDeCodes.put(temp.getValue(), temp.getKey()); } } /** * 輸出 編碼表 */ public void hufumanCodesList() { for(Map.Entry<Byte, String> map : huffmanCodes.entrySet()) { System.out.print("[ Byte = " + map.getKey() + ", String = " + map.getValue() + " ] ==> "); } } /** * 輸出 解碼錶 */ public void hufumanDeCodesList() { for(Map.Entry<String, Byte> map : huffmanDeCodes.entrySet()) { System.out.print("[ String = " + map.getKey() + ", Byte = " + map.getValue() + " ] ==> "); } } /** * 將 字符串 對應的位元組數組,根據 編碼表 轉為 對應的 二進制串。 * 將 二進制串 以 8 位為 一個單位,進一步轉為 位元組數組 * @param arrays 待壓縮的位元組數組(字符串轉換的位元組數組) * @return 壓縮後的位元組數組 */ public byte[] convertAndCompress(byte[] arrays) { // 根據 編碼表,將 位元組數組 轉為對應的 二進制串 並 拼接 StringBuilder stringBuilder = new StringBuilder(); for (byte temp : arrays) { stringBuilder.append(huffmanCodes.get(temp)); } // System.out.println("轉換的二進制串為: " + stringBuilder.toString()); // 以 8 位二進制為單位,將 二進制串 轉為位元組數組,不足 8 位 按 8 位處理,並額外增加一個位元組用於記錄其實際長度。 // byte[] result = new byte[stringBuilder.length() % 8 == 0 ? stringBuilder.length() / 8 : stringBuilder.length() / 8 + 1]; byte[] result = new byte[(stringBuilder.length() + 7) / 8 + 1]; for(int i = 0, j = 0; i < result.length && j < stringBuilder.length(); i++, j += 8) { if (j + 8 < stringBuilder.length()) { /** * 整數使用 補碼 的形式存儲, * 正數的 補碼、反碼、原碼 均相同。 * 負數的 補碼為 反碼 加 1。 * 反碼為 符號位不變,其餘各位取反。 * 比如: 1110 0110,其符號位為 1,表示負數,則其轉為整數後 為 其反碼 加 1,即 1001 1010,即 -26 */ result[i] = (byte)Integer.parseInt(stringBuilder.substring(j, j + 8), 2); } else { // 額外增加一個位元組用於記錄其實際長度,若 恰好為 8 位,則記錄 8 位,否則 記錄 1 ~ 7 result[i] = (byte)Integer.parseInt(stringBuilder.substring(j), 2); result[i + 1] = (byte)stringBuilder.substring(j).length(); } } return result; } /** * 將壓縮後的位元組數組 轉為 二進制字符串,並根據 編碼表(解碼錶) 轉為 位元組數組 * @param arrays 壓縮後的位元組數組 * @return 解壓後的位元組數組 */ public byte[] deCompressAndConvert(byte[] arrays) { // 用於字符串拼接 StringBuilder stringBuilder = new StringBuilder(); // 遍歷壓縮後的位元組數組,轉為對應的 二進制 字符串 for (int i = 0; i < arrays.length - 1; i++) { /** * 使用 Integer.toBinaryString() 可以將 int 型 轉為 二進制 字符串。 * 所以先將 byte 轉為 int,但由於 int 為 4 位元組,byte 為 1 位元組,所以需要截取 int 後 8 位作為 byte 對應的 二進制字符串。 * Integer.toBinaryString() 對於非負數,其前面的 0 會默認不顯示,可能造成不足 8 位的情況,所以需要對其 進行 補位。 * 比如: * Integer.toBinaryString(5) 輸出為 101,但其真實對應的應該為 0000 0101, * 可以使用 5 | 256 的方式,即 101 | 1 0000 0000 進行 按位與運算。結果為 1 0000 0101,再截取 後 8 位即為對應的 二進制字符串。 * * Integer.toBinaryString() 對於負數,轉換為 int 後,會顯示 32 位,首位為 1,所以無需補位,直接截取低 8 位即可。 * * 倒數最後一個位元組,表示 倒數第二個位元組 實際轉換的 二進制串 位數, * 所以 處理倒數第二個位元組時,需要根據 倒數最後一個位元組 進行 字符串截取操作。 */ int temp = arrays[i]; // 低 8 位 與 1 0000 0000 進行按位與運算,比如: 101 | 1 0000 0000 = 1 0000 0101 temp |= 256; String str = Integer.toBinaryString(temp); // 若當前為倒數第二個位元組,則根據 倒數第一個位元組 記錄的值 去截取 倒數第二個位元組 的實際字符串 if (i + 1 == arrays.length - 1) { stringBuilder.append(str.substring(arrays[i + 1] + 1)); } else { stringBuilder.append(str.substring(str.length() - 8)); } } // 根據 編碼集 得到 解碼集 getDeCodes(huffmanCodes); System.out.println("輸出編碼表 對應的 解碼錶: "); hufumanDeCodesList(); System.out.println("\n==============================="); // 保存轉換的二進制字符串 List<Byte> list = new ArrayList<>(); // 根據解碼集,將 二進制字符串 轉換成 位元組數組 for(int i = 0, j = 1; j <= stringBuilder.length(); j++) { Byte temp = huffmanDeCodes.get(stringBuilder.substring(i, j)); if (temp != null) { list.add(temp); i = j; } } // 第一種返回方式:Byte[] newResult = list.toArray(new Byte[list.size()]); // 第二種返回方式: byte[] result = new byte[list.size()]; for(int i = 0; i < list.size(); i++) { result[i] = list.get(i); } return result; } } /** * 定義樹節點 */ class TreeNode5 implements Comparable<TreeNode5> { Byte data; // 保存節點數據 Long value; // 保存節點權值(字符出現頻率) TreeNode5 left; // 保存左子節點 TreeNode5 right; // 保存右子節點 @Override public int compareTo(TreeNode5 o) { return (int)(this.value - o.value); } public TreeNode5(Byte data, Long value) { this.data = data; this.value = value; } @Override public String toString() { return "TreeNode5{ data = " + data + ", value = " + value + " }"; } /** * 前序遍歷 */ public void prefixList() { // 輸出當前節點 System.out.print(this + " "); // 遍歷左子節點 if (this.left != null) { this.left.prefixList(); } // 遍歷右子節點 if (this.right != null) { this.right.prefixList(); } } } 【輸出結果:】 當前字符串為: Java C++ 轉為位元組數組為: [74, 97, 118, 97, 32, 67, 43, 43] 位元組數組轉哈夫曼樹後,前序遍歷輸出哈夫曼樹: TreeNode5{ data = null, value = 8 } TreeNode5{ data = null, value = 4 } TreeNode5{ data = 97, value = 2 } TreeNode5{ data = 43, value = 2 } TreeNode5{ data = null, value = 4 } TreeNode5{ data = null, value = 2 } TreeNode5{ data = 32, value = 1 } TreeNode5{ data = 67, value = 1 } TreeNode5{ data = null, value = 2 } TreeNode5{ data = 118, value = 1 } TreeNode5{ data = 74, value = 1 } =============================== 輸出當前哈夫曼樹 葉子節點 對應的編碼表: [ Byte = 32, String = 100 ] ==> [ Byte = 97, String = 00 ] ==> [ Byte = 67, String = 101 ] ==> [ Byte = 118, String = 110 ] ==> [ Byte = 74, String = 111 ] ==> [ Byte = 43, String = 01 ] ==> =============================== 壓縮前的位元組數組為: [74, 97, 118, 97, 32, 67, 43, 43] 壓縮後的位元組數組為: [-26, 37, 5, 4] =============================== 輸出編碼表 對應的 解碼錶: [ String = 00, Byte = 97 ] ==> [ String = 110, Byte = 118 ] ==> [ String = 100, Byte = 32 ] ==> [ String = 111, Byte = 74 ] ==> [ String = 01, Byte = 43 ] ==> [ String = 101, Byte = 67 ] ==> =============================== 解壓後的位元組數組為: [74, 97, 118, 97, 32, 67, 43, 43] 解壓後的字符串為:Java C++
9、二叉排序樹(二叉搜索樹、BST)
(1)什麼是 BST?
BST 可以是 Binary Sort Tree 的縮寫(二叉排序樹),也可以是 Binary Search Sort 的縮寫(二叉搜索樹)。其查詢效率 相比於 鏈式結構 高。
【BST 特點:】
對於一顆二叉樹,其滿足如下定義:
任何一個非葉子節點,其左子節點的值 小於 當前節點。
任何一個非葉子節點,其右子節點的值 大於 當前節點。
註:
若存在 節點相等的情況,可以將該節點 放在 左子節點 或者 右子節點 處。
即 二叉排序樹可能存在三種定義:
左子節點 小於等於 當前節點,右子節點 大於 當前節點。
左子節點 小於 當前節點,右子節點 大於等於 當前節點。
左子節點 小於 當前節點,右子節點 大於 當前節點。

(2)BST 增、刪、查 操作
此處規定 左子節點 小於 當前節點,右子節點 大於等於 當前節點。
【添加節點:】 若 待添加節點 小於 當前節點,則 遞歸向 當前節點 左子節點 進行添加操作。 若 待添加節點 大於等於 當前節點,則 遞歸向 當前節點 右子節點 進行添加操作。 【查找節點:】 若 待查找節點 等於 當前節點,則 查找成功。 若 待查找節點 小於 當前節點,則 遞歸向 左子節點 查找。 若 待查找節點 大於等於 當前節點,則 遞歸向 右子節點 查找。 【刪除節點:】 刪除節點可能存在三種情況: 刪除的是 葉子節點。 刪除的是 非葉子節點,且 只有一個子節點。 刪除的是 非葉子節點,且 有兩個子節點。 若刪除的是 葉子節點: Step1:先去查找需要刪除的節點是否存在,存在則進行下面操作。 Step2:若刪除節點為 根節點,則根節點直接置 null。即 root = null; Step3:若刪除節點不是 根節點,則 找到 待刪除節點的 父節點, 若 待刪除節點為 父節點 的 左子節點,則將左子節點置 null。即 parent.left = null; 若 待刪除節點為 父節點 的 右子節點,則將右子節點置 null。即 parent.right = null; 若刪除的是 非葉子節點,且 只有一個子節點。 Step1 同上。 Step2:若刪除節點為 根節點,則根節點直接指向 子節點即可。 Step3:找到 待刪除節點的 父節點,並判斷 待刪除節點 子節點 是 左子節點 還是 右子節點。 若 待刪除節點為 父節點 的 左子節點,且 待刪除節點 存在 左子節點,則 父節點的 左子節點 直接指向 刪除節點的左子節點。即 parent.left = node.left; 若 待刪除節點為 父節點 的 左子節點,且 待刪除節點 存在 右子節點,則 父節點的 左子節點 直接指向 刪除節點的右子節點。即 parent.left = node.right; 若 待刪除節點為 父節點 的 右子節點,且 待刪除節點 存在 左子節點,則 父節點的 右子節點 直接指向 刪除節點的左子節點。即 parent.right = node.left; 若 待刪除節點為 父節點 的 右子節點,且 待刪除節點 存在 右子節點,則 父節點的 右子節點 直接指向 刪除節點的右子節點。即 parent.right = node.right; 若刪除的是 非葉子節點,且 有兩個子節點。 Step1 同上。 Step2:找到 待刪除節點,並找到 其右子樹最小值 或者 左子樹最大值, 刪除找到的節點,並將其值置於 待刪除節點處。 即 保證將 左子樹 的最大值 放置到 中間節點 或者 將 右子樹 最小值 放到中間節點。 使得 左子樹的所有節點 小於 中間節點, 右子樹的所有節點 大於等於 中間節點。 【代碼實現:】 package com.lyh.tree; import java.util.ArrayList; import java.util.Arrays; import java.util.List; public class BinarySearchTree { private TreeNode7 root; // 設置根節點 public static void main(String[] args) { // 構造二叉排序樹 BinarySearchTree binarySearchTree = new BinarySearchTree(); int[] arrays = new int[]{7, 3, 10, 12, 5, 1, 9}; for (int temp : arrays) { binarySearchTree.addNote(temp); } // 輸出原數組 System.out.println("原數組為: " + Arrays.toString(arrays)); System.out.println("======================================"); // 輸出中序遍歷結果 System.out.println("二叉排序樹中序遍歷結果為: " + binarySearchTree.infixList()); System.out.println("======================================"); // 輸出查找結果 System.out.println("查找 10: " + binarySearchTree.search(10)); System.out.println("查找 20: " + binarySearchTree.search(20)); System.out.println("查找 9: " + binarySearchTree.search(9)); System.out.println("======================================"); // 輸出查找節點的父節點 System.out.println("查找 9: " + binarySearchTree.searchParent(9)); System.out.println("查找 7: " + binarySearchTree.searchParent(7)); System.out.println("======================================"); // 輸出刪除後的 二叉搜索樹 for (int i = 0; i < arrays.length; i++) { System.out.println("刪除 " + arrays[i] + " : " + binarySearchTree.deleteNode(arrays[i])); System.out.println("二叉排序樹中序遍歷結果為: " + binarySearchTree.infixList()); System.out.println("======================================"); } } /** * 添加節點 * @param data 數據 */ public void addNote(int data) { if (root == null) { root = new TreeNode7(data); return; } root.addNode(new TreeNode7(data)); } /** * 中序遍歷 * @return 中序遍歷結果 */ public List infixList() { if (root == null) { System.out.println("為空樹"); return null; } return root.infixList(new ArrayList()); } /** * 查找節點 * @param data 待查找數據 * @return 若查找失敗返回 null */ public TreeNode7 search(int data) { // 根節點不存在時,返回 null if (root == null) { return null; } return root.search(data); } /** * 查找節點的父節點 * @param data 待查找數據 * @return 若查找失敗返回 null */ public TreeNode7 searchParent(int data) { // 根節點不存在時,返回 null if (root == null) { return null; } return root.searchParent(data); } /** * 刪除節點 * @param data 待刪除節點 * @return 刪除失敗返回 -1,刪除成功返回 0 */ public int deleteNode(int data) { // 先查找 待刪除節點 是否存在 TreeNode7 node = search(data); // 刪除節點存在,則進行刪除操作 if (node != null) { // 查找待刪除節點的父節點 TreeNode7 parent = searchParent(data); // 刪除節點不為根節點時, // 若刪除的是 葉子節點,則判斷當前 刪除節點為 父節點的左子節點 還是 右子節點 if (node.left == null && node.right == null) { // parent 為空,則刪除節點為 根節點,直接將 根節點置 null if (parent == null) { root = null; return 0; } if (parent.left != null && parent.left.data == data) { parent.left = null; } else { parent.right = null; } return 0; } // 若刪除的是 非葉子節點,且只有一個 左子節點。 if (node.left != null && node.right == null) { // parent 為空,則刪除節點為 根節點,直接賦值為 左子節點 即可 if (parent == null) { root = node.left; return 0; } // 若待刪除節點為 父節點的左子節點 if (parent.left != null && parent.left.data == data) { parent.left = node.left; } else { // 若 待刪除節點為 父節點的 右子節點 parent.right = node.left; } return 0; } // 若刪除的是 非葉子節點,且只有一個 右子節點 if (node.right != null && node.left == null) { // parent 為空,則刪除節點為 根節點,直接賦值為 右子節點 即可 if (parent == null) { root = node.right; return 0; } // 若待刪除節點為 父節點的左子節點 if (parent.left != null && parent.left.data == data) { parent.left = node.right; } else { // 若 待刪除節點為 父節點的 右子節點 parent.right = node.right; } return 0; } // 若刪除的是 非葉子節點,且有兩個 子節點 // 找到 右子樹 最小值,並覆蓋 待刪除節點,則滿足 二叉搜索樹條件 TreeNode7 minRightNode = node.right; while(minRightNode.left != null) { minRightNode = minRightNode.left; } // 記錄 右子樹最小值 int minRightData = minRightNode.data; // 刪除 右子樹最小值 deleteNode(minRightData); // 將最小值 覆蓋 待刪除節點,即完成 刪除操作 node.data = minRightData; return 0; } // 刪除節點不存在,返回 -1,表示刪除失敗 return -1; } } /** * 定義樹節點 */ class TreeNode7 { int data; // 保存節點數據 TreeNode7 left; // 保存 左子節點 TreeNode7 right; // 保存 右子節點 public TreeNode7(int data) { this.data = data; } @Override public String toString() { return "TreeNode7{ data = " + data + ", left = " + left + ", right = " + right + " }"; } /** * 中序遍歷 * @param result 中序遍歷結果 * @return 中序遍歷結果 */ public List infixList(List result) { // 遞歸遍歷 左子節點 if (this.left != null) { this.left.infixList(result); } // 保存 當前節點 result.add(this.data); // 遞歸遍歷 右子節點 if (this.right != null) { this.right.infixList(result); } return result; } /** * 添加節點 * @param node 節點 */ public void addNode(TreeNode7 node) { // 節點不存在時,不添加 if (node == null) { return; } // 節點存在時 if (this.data > node.data) { // 數據小於當前節點時,在左子樹進行添加 if (this.left != null) { this.left.addNode(node); } else { this.left = node; } } else { // 數據大於等於當前節點是,在右子樹進行添加 if (this.right != null) { this.right.addNode(node); } else { this.right = node; } } } /** * 查找節點 * @param data 待查找數據 * @return 查找失敗返回 null */ public TreeNode7 search(int data) { // 當前節點 即為 待查找節點 if (this.data == data) { return this; } // 若 當前節點 大於 待查找節點,則遞歸左子樹進行查找 if (this.data > data && this.left != null) { return this.left.search(data); } // 若 當前節點 小於等於 待查找節點,則遞歸右子樹進行查找 if (this.data <= data && this.right != null) { return this.right.search(data); } // 查找失敗返回 null return null; } /** * 查找節點 * @param data 待查找數據 * @return 查找失敗返回 null */ public TreeNode7 searchParent(int data) { // 若當前節點 左子樹 或者 右子樹 查找數據成功,返回 當前節點 if ((this.left != null && this.left.data == data) || (this.right != null && this.right.data == data)) { return this; } // 若 當前節點 大於 待查找節點,則遞歸 左子樹查找 if (this.data > data && this.left != null) { return this.left.searchParent(data); } // 若 當前節點 小於等於 待查找節點,則遞歸 右子樹查找 if (this.data <= data && this.right != null) { return this.right.searchParent(data); } // 查找失敗,返回 null return null; } } 【輸出結果:】 原數組為: [7, 3, 10, 12, 5, 1, 9] ====================================== 二叉排序樹中序遍歷結果為: [1, 3, 5, 7, 9, 10, 12] ====================================== 查找 10: TreeNode7{ data = 10, left = TreeNode7{ data = 9, left = null, right = null }, right = TreeNode7{ data = 12, left = null, right = null } } 查找 20: null 查找 9: TreeNode7{ data = 9, left = null, right = null } ====================================== 查找 9: TreeNode7{ data = 10, left = TreeNode7{ data = 9, left = null, right = null }, right = TreeNode7{ data = 12, left = null, right = null } } 查找 7: null ====================================== 刪除 7 : 0 二叉排序樹中序遍歷結果為: [1, 3, 5, 9, 10, 12] ====================================== 刪除 3 : 0 二叉排序樹中序遍歷結果為: [1, 5, 9, 10, 12] ====================================== 刪除 10 : 0 二叉排序樹中序遍歷結果為: [1, 5, 9, 12] ====================================== 刪除 12 : 0 二叉排序樹中序遍歷結果為: [1, 5, 9] ====================================== 刪除 5 : 0 二叉排序樹中序遍歷結果為: [1, 9] ====================================== 刪除 1 : 0 二叉排序樹中序遍歷結果為: [9] ====================================== 刪除 9 : 0 為空樹 二叉排序樹中序遍歷結果為: null ======================================
10、平衡二叉樹(AVL)
(1)什麼是 平衡二叉樹?
平衡二叉樹(Balanced Binary Tree)也稱為 自平衡二叉搜索樹(Self Balanced Binary Search Tree),也稱為 AVL 樹(人名縮寫)。用於提高 二叉搜索樹 的查詢效率。
其本質上 仍是 一顆 二叉搜索樹,只是其會自動 旋轉節點(平衡條件),用於保證 樹的高度。
平衡條件:
每個節點 的 左、右子樹 的高度差的絕對值 不超過 1。且 左、右兩個子樹 也是 平衡二叉樹。
普通 二叉搜索樹 構建如下:
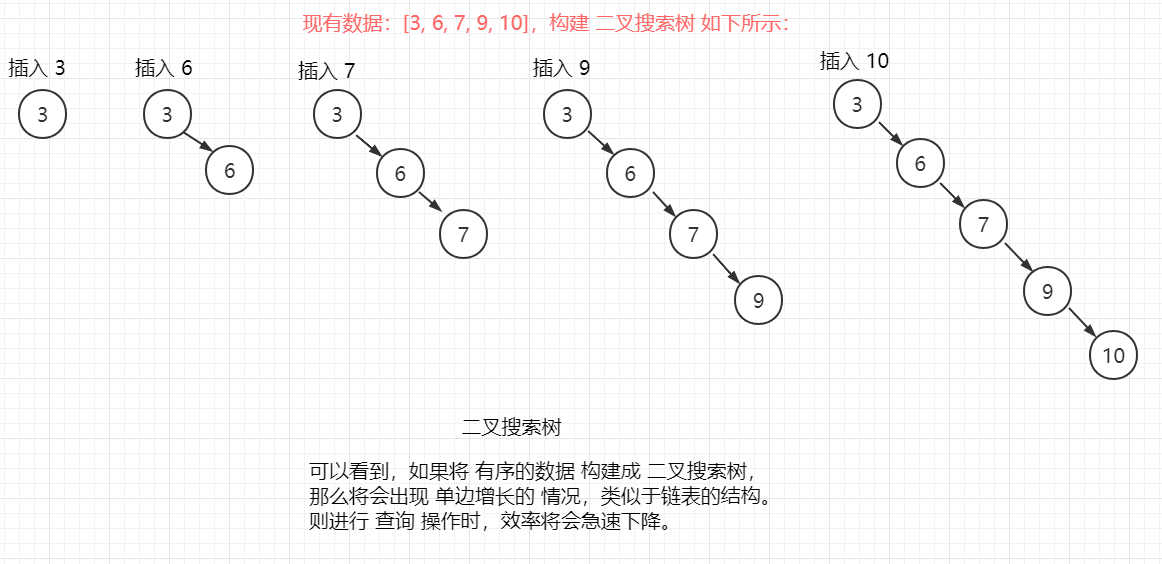
平衡二叉搜索樹構建如下:
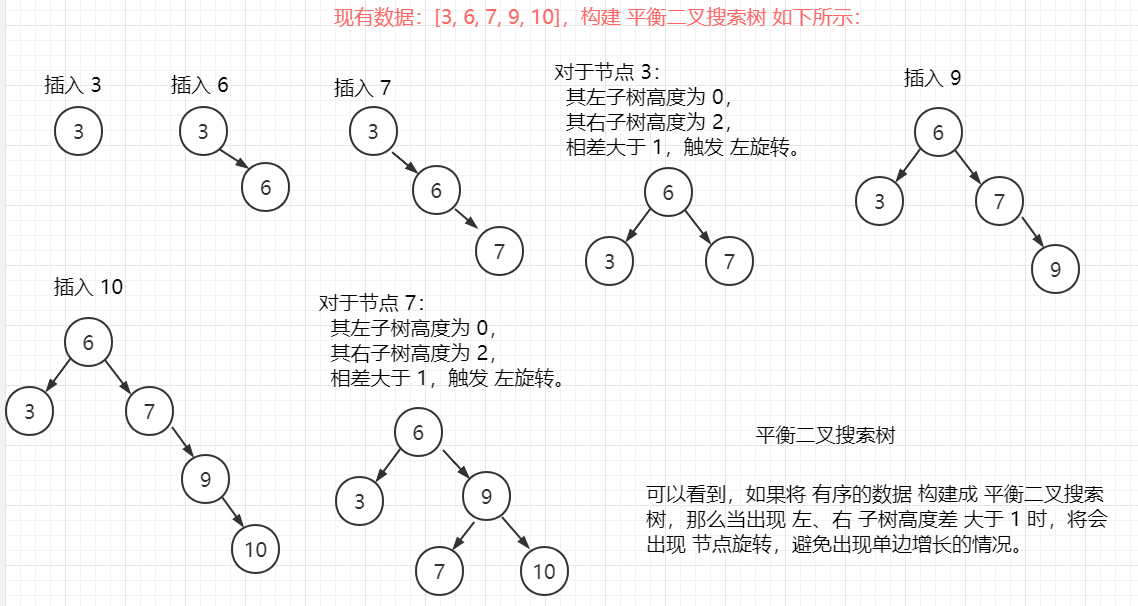
(2)如何實現平衡?
當 左、右子樹 出現高度差 大於 1 時,為了實現平衡,節點需要進行旋轉。
【節點的 高度、深度:(此處僅個人理解,有不對的地方還望不吝賜教)】 當前節點的高度:從 當前節點 開始 到 葉子節點 最長路徑 的節點數。 當前節點的深度:從 根節點 開始 到當前節點 最長路徑 的節點數。 註: 此處假定 節點不存在時為 0。節點存在記為 1。 雖然樹的 高度、深度相同,但具體到 某個節點的 高度、深度 不一定相同。 比如: A B C E F G 如上圖所示, B 節點 高度為 3(B->E->G,3個節點),深度為 2(A->B,2個節點)。 C 節點高度為 2(C->F,2個節點),深度為 2(A->C,兩個節點)。 【旋轉類型:】 左旋轉。 右旋轉。 雙旋轉(左旋轉、右旋轉)。 【左旋轉:】 左子樹高度 小於 右子樹高度,且 高度差 大於 1, 此時 需要將 右子樹節點 向左旋轉,降低 右子樹的高度。 步驟(某個節點需要旋轉時): Step1:創建一個新的節點,用於保存 當前節點的值。 Step2:將新節點的左子樹 設置成 當前節點的 左子樹。 Step3:將新節點的右子樹 設置成 當前節點的 右子樹的左子樹。 Step4:將當前節點的值 設置成 右子樹根節點的值。 Step5:將當前節點的右子樹 設置成 右子樹的右子樹。 Step6:將當前節點的左子樹 設置成 新節點。 【右旋轉:】 左子樹高度 大於 右子樹高度,且 高度差 大於 1, 此時 需要將 左子樹節點 向右旋轉,降低 左子樹的高度。 步驟(某個節點需要旋轉時): Step1:創建一個新的節點,用於保存 當前節點的值。 Step2:將新節點的右子樹 設置成 當前節點的 右子樹。 Step3:將新節點的左子樹 設置成 當前節點的 左子樹的右子樹。 Step4:將當前節點的值 設置成 左子樹根節點的值。 Step5:將當前節點的左子樹 設置成 右子樹的左子樹。 Step6:將當前節點的右子樹 設置成 新節點。 【單一 左旋轉、右旋轉 出現的問題:】 只存在 左旋轉、右旋轉時,可能造成 死循環。需要兩者結合使用。 比如: 插入節點 C 如下: A B C A 節點右子樹高度為 2,左子樹高度為 1,需要進行 左旋轉。 左旋轉後: B A C 此時,B 節點左子樹高度為 2,右子樹高度為 1,需要進行 右旋轉。 右旋轉後: A B C 發現右旋轉後,又回到了最初的起點。從而出現死循環。 【雙旋轉:】 結合左旋轉、右旋轉。 先旋轉 子節點,再旋轉 當前節點。 步驟(存在兩種情況): 情況一(當前節點符合右旋轉時): 若當前節點 左子樹 的 右子樹的高度 大於 左子樹 的 左子樹的高度, 則先 對 當前節點的 左節點 進行 左旋轉。 然後再 對當前節點 進行 右旋轉。 情況二(當前節點符合左旋轉時): 若當前節點 右子樹 的 左子樹的高度 大於 右子樹的 右子樹的高度, 則 先對 當前節點的 右節點 進行 右旋轉。 然後再 對當前節點進行左旋轉。
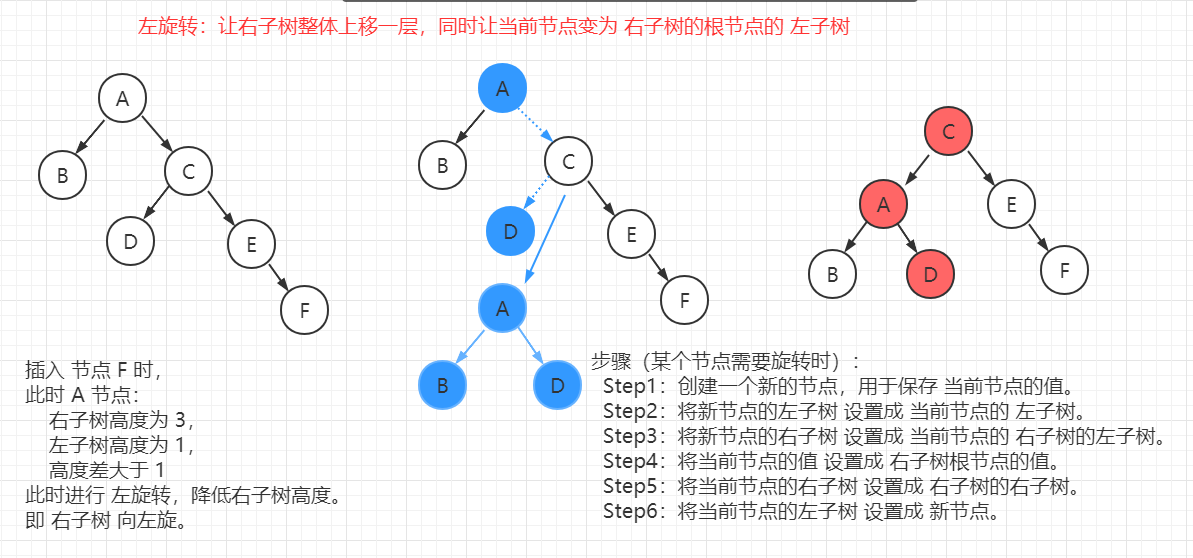
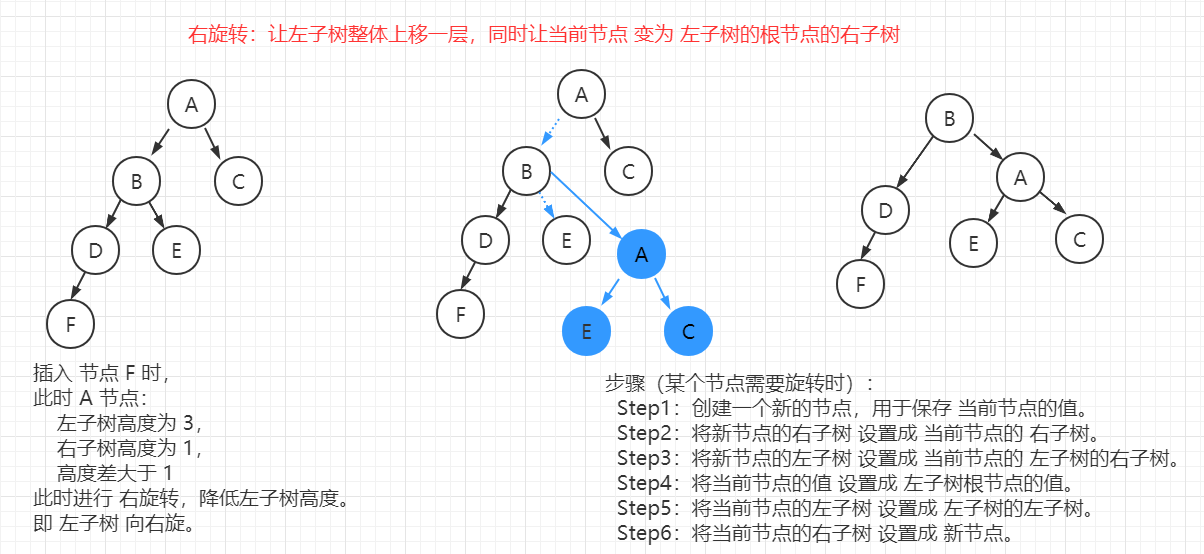


(3)代碼實現
【代碼實現:】 package com.lyh.tree; import java.util.ArrayList; import java.util.Arrays; import java.util.List; public class BalanceBinarySearchTree { private TreeNode8 root; // 設置根節點 public static void main(String[] args) { int[] arrays = new int[]{3, 6, 7, 9, 10}; // int[] arrays = new int[]{10, 11, 7, 6, 8, 9}; System.out.println("原數組為: " + Arrays.toString(arrays)); System.out.println("====================================="); // 構建普通的 二叉搜索樹 System.out.println("構建普通 二叉搜索樹:"); BalanceBinarySearchTree balanceBinarySearchTree2 = new BalanceBinarySearchTree(); for (int temp : arrays) { balanceBinarySearchTree2.addNote2(temp); } System.out.println("中序遍歷為: " + balanceBinarySearchTree2.infixList()); // 輸出根節點、以及根節點高度 System.out.println(balanceBinarySearchTree2.root); System.out.println(balanceBinarySearchTree2.root.getHeight()); System.out.println("====================================="); // 構建 平衡二叉樹 System.out.println("構建平衡二叉樹:"); BalanceBinarySearchTree balanceBinarySearchTree = new BalanceBinarySearchTree(); for (int temp : arrays) { balanceBinarySearchTree.addNote(temp); } System.out.println("中序遍歷為: " + balanceBinarySearchTree.infixList()); // 輸出根節點、以及根節點高度 System.out.println(balanceBinarySearchTree.root); System.out.println(balanceBinarySearchTree.root.getHeight()); System.out.println("====================================="); } /** * 添加節點(平衡二叉搜索樹 添加節點的方式,節點會旋轉) * @param data 數據 */ public void addNote(int data) { if (root == null) { root = new TreeNode8(data); return; } root.addNode(new TreeNode8(data)); } /** * 添加節點(普通 二叉搜索樹 添加節點的方式) * @param data 數據 */ public void addNote2(int data) { if (root == null) { root = new TreeNode8(data); return; } root.addNode2(new TreeNode8(data)); } /** * 中序遍歷 * @return 中序遍歷結果 */ public List infixList() { if (root == null) { System.out.println("為空樹"); return null; } return root.infixList(new ArrayList()); } } /** * 定義樹節點 */ class TreeNode8 { int data; // 保存節點數據 TreeNode8 left; // 保存 左子節點 TreeNode8 right; // 保存 右子節點 public TreeNode8(int data) { this.data = data; } @Override public String toString() { return "TreeNode8{ data = " + data + ", left = " + left + ", right = " + right + " }"; } /** * 中序遍歷 * * @param result 中序遍歷結果 * @return 中序遍歷結果 */ public List infixList(List result) { // 遞歸遍歷 左子節點 if (this.left != null) { this.left.infixList(result); } // 保存 當前節點 result.add(this.data); // 遞歸遍歷 右子節點 if (this.right != null) { this.right.infixList(result); } return result; } /** * 添加節點(平衡二叉搜索樹 添加節點的方式,節點會旋轉) * @param node 節點 */ public void addNode(TreeNode8 node) { // 節點不存在時,不添加 if (node == null) { return; } // 節點存在時 if (this.data > node.data) { // 數據小於當前節點時,在左子樹進行添加 if (this.left != null) { this.left.addNode(node); } else { this.left = node; } } else { // 數據大於等於當前節點是,在右子樹進行添加 if (this.right != null) { this.right.addNode(node); } else { this.right = node; } } // 添加節點後需要判斷 當前節點是否需要旋轉 // 當前節點左子樹高度 大於 右子樹高度,且差值超過 1,則需要進行 右旋轉 if (this.getLeftHeight() - this.getRightHeight() > 1) { // 當前節點 左子樹 的左子節點高度 小於 左子樹 的右子節點高度時,需要先對 左子樹進行 左旋轉 if (this.left != null && this.left.getLeftHeight() < this.left.getRightHeight()) { this.left.leftRotate(); } // 當前節點進行右旋轉 this.rightRotate(); return; } // 當前節點右子樹高度 大於 左子樹高度,其差值超過 1,則需要進行 左旋轉 if (this.getRightHeight() - this.getLeftHeight() > 1) { // 當前節點 右子樹 的左子節點高度 大於 右子樹 的右子節點高度時,需要先對 右子樹進行 右旋轉 if (this.right != null && this.right.getLeftHeight() > this.right.getRightHeight()) { this.right.rightRotate(); } // 當前節點進行左旋轉 this.leftRotate(); } } /** * 添加節點(普通 二叉搜索樹 添加節點的方式) * @param node 節點 */ public void addNode2(TreeNode8 node) { // 節點不存在時,不添加 if (node == null) { return; } // 節點存在時 if (this.data > node.data) { // 數據小於當前節點時,在左子樹進行添加 if (this.left != null) { this.left.addNode2(node); } else { this.left = node; } } else { // 數據大於等於當前節點是,在右子樹進行添加 if (this.right != null) { this.right.addNode2(node); } else { this.right = node; } } } /** * 返回節點的高度 * @return 節點的高度,節點不存在則返回 0。 */ public int getHeight() { return this == null ? 0 : Math.max(this.getLeftHeight(), this.getRightHeight()) + 1; } /** * 返回 左子樹 的高度 * @return 左子樹的高度 */ public int getLeftHeight() { return this.left == null ? 0 : this.left.getHeight(); } /** * 返回 右子樹 的高度 * @return 右子樹的高度 */ public int getRightHeight() { return this.right == null ? 0 : this.right.getHeight(); } /** * 節點進行左旋轉 */ public void leftRotate() { // 創建一個新節點,並保存當前節點的值 TreeNode8 newNode = new TreeNode8(this.data); // 新節點的 左子樹設置成 當前節點的左子樹 newNode.left = this.left; // 新節點的 右子樹設置成 當前節點的 右子樹的左子樹 newNode.right = this.right.left; // 當前節點的值 設置成 其右子樹 根節點的值 this.data = this.right.data; // 當前節點的 左子樹 設置成 新節點 this.left = newNode; // 當前節點的 右子樹 設置成 其右子樹的右子樹 this.right = this.right.right; } /** * 節點進行右旋轉 */ public void rightRotate() { // 創建一個新節點,用於保存當前節點的值 TreeNode8 newNode = new TreeNode8(this.data); // 新節點的 左子樹設置成 當前節點的 左子樹的右子樹 newNode.left = this.left.right; // 新節點的 右子樹設置成 當前節點的 右子樹 newNode.right = this.right; // 當前節點的值 設置成 其左子樹 根節點的值 this.data = this.left.data; // 當前節點的 左子樹 設置成 其左子樹的左子樹 this.left = this.left.left; // 當前節點的 右子樹 設置成 其右子樹的右子樹 this.right = newNode; } } 【輸出結果:】 原數組為: [3, 6, 7, 9, 10] ===================================== 構建普通 二叉搜索樹: 中序遍歷為: [3, 6, 7, 9, 10] TreeNode8{ data = 3, left = null, right = TreeNode8{ data = 6, left = null, right = TreeNode8{ data = 7, left = null, right = TreeNode8{ data = 9, left = null, right = TreeNode8{ data = 10, left = null, right = null } } } } } 5 ===================================== 構建平衡二叉樹: 中序遍歷為: [3, 6, 7, 9, 10] TreeNode8{ data = 6, left = TreeNode8{ data = 3, left = null, right = null }, right = TreeNode8{ data = 9, left = TreeNode8{ data = 7, left = null, right = null }, right = TreeNode8{ data = 10, left = null, right = null } } } 3 =====================================