LeetCode刷題總結-數組篇(中)
- 2019 年 11 月 6 日
- 筆記
本文接着上一篇文章《LeetCode刷題總結-數組篇(上)》,繼續講第二個常考問題:矩陣問題。
矩陣也可以稱為二維數組。在LeetCode相關習題中,作者總結髮現主要考點有:矩陣元素的遍歷、矩陣位置的旋轉、矩陣行或列次序的交換、空間複雜度為O(1)等。本期共12道題,2道簡單題,8道中等題,2道困難題。
- 例1是楊輝三角的一個延申題,是一道非常經典的矩陣習題,本題理想解法是動態規劃,但是也可以採用遞歸來求解。
- 例2是一道順時針訪問矩陣元素的習題,在不少面試題中有見到。
- 例3、例4和例5則強調如果利用矩陣本身的空間,來變換矩陣中的元素,即空間複雜度為O(1)。用到了元素間交換和位運算策略,其中相關解法很巧妙。
- 例6是一道如何移動矩陣的問題。
- 例7和例8則是考察我們快速理解題意,並在較短時間內完成較高質量代碼的能力。即編寫的代碼爭取一次性通過。
- 例9考察我們如何把二分查找的應用場景由一維數組轉換到二維數組。
- 例10是一道動態規劃結合矩陣的經典習題,並且還可以延申出求最短路徑的問題。
- 例11則很有意思,該題是上篇例6中《和為K的子數組》的一個升級版,把一維數組的場景變換成了二維的場景,並結合了動態思想,因此題目難度由中等變成了困難。
- 例12是一道困難級別的習題,該題主要考察如何我們的數學分析能力,如何靈活變換矩陣的行和列,以及細節處理能力。
例1 楊輝三角 II
題號:119,難度:簡單(可參考 楊輝三角,題號:118,難度:簡單)
題目描述:

解題思路:
依據楊輝三角的規律,當前行的數據和上一行的數據有着遞推關係:dp[i][j] = dp[i-1][j-1] + dp[i-1][j]。依據該遞推公式可以寫一個較為清晰的動態規劃解法,其空間複雜度為O(k)。但是,也可以採用遞歸的思想來解決。此處提供一個應用遞歸思想來解決該問題的代碼。
具體代碼:
class Solution { public List<Integer> getRow(int rowIndex) { List<Integer> result = new ArrayList<>(); if(rowIndex + 1 <= 0) return result; dfs(result, rowIndex+1); return result; } public void dfs(List<Integer> result, int rowIndex) { if(rowIndex == 1) { result.add(1); return; } dfs(result, rowIndex - 1); int len = result.size(); int temp = 1; for(int i = 1;i < len;i++) { int t = result.get(i); result.set(i, temp+result.get(i)); temp = t; } result.add(1); } }
執行結果:

例2 螺旋矩陣
題號:54,難度:中等
題目描述:

解題思路:
這題只需要不停的往內順時針旋轉訪問即可。但是,在實現代碼時需要注意邊界的問題。另外,依據LeetCode上評論的解答思路,可以給訪問過的元素做一個標記,或者統計當前已經訪問的元素個數,這樣更加有利於判斷訪問結束的時間節點。
具體代碼:
class Solution { public List<Integer> spiralOrder(int[][] matrix) { if(matrix.length == 0) return new ArrayList<Integer>(); List<Integer> result = new ArrayList<>(); int start_x = 0, start_y = 0; int max_x = matrix.length, max_y = matrix[0].length; int len = matrix.length * matrix[0].length; while(result.size() < len) { int x = start_x, y = start_y; for(;y < max_y && result.size() < len;y++) result.add(matrix[x][y]); // 向右 y = y -1; for(x = x + 1;x < max_x && result.size() < len;x++) result.add(matrix[x][y]); // 向下 x = x - 1; for(y = y -1;y >= start_y && result.size() < len;y--) result.add(matrix[x][y]); // 向左 y = y + 1; for(x = x - 1;x > start_x && result.size() < len;x--) result.add(matrix[x][y]); // 向上 max_x--; max_y--; start_x++; start_y++; } return result; } }
執行結果:

例3 旋轉圖像
題號:48,難度:中等
題目描述:

解題思路:
這題可以理解為是例2的一個演化版。題目意思說明為n*n的矩陣,所以不用考慮長方形矩陣的情形。下面代碼給出的解答思路為依據正方形矩陣不停往內進行旋轉轉圈,每次轉動的步數為邊長長度減去1的大小,每往內旋轉一步,正方形邊長減2。另外,看到LeetCode評論的解答思路,有一個很有意思:把矩陣翻轉兩次,第一次沿着主對角線翻轉,第二次沿着垂直中線翻轉。
具體代碼:
class Solution { public void rotate(int[][] matrix) { for(int i = 0;i < matrix.length;i++) { int len = matrix.length - i * 2; while(--len > 0) { int temp = matrix[i][i]; // 左移 for(int j = i + 1;j < matrix.length - i;j++) temp = swap(matrix, i, j, temp); // 下移 for(int j = i + 1;j < matrix.length - i;j++) temp = swap(matrix, j, matrix.length - i -1, temp); } // 右移 for(int j = matrix.length - i - 2;j >= i;j--) temp = swap(matrix, matrix.length - i -1, j, temp); // 上移 for(int j = matrix.length - i - 2;j >= i;j--) temp = swap(matrix, j, i, temp); } } } public int swap(int[][] matrix, int i, int j, int temp) { int t = matrix[i][j]; matrix[i][j] = temp; return t; } }
執行結果:
例4 矩陣置零
題號:73,難度:中等
題目描述:

解題思路:
先說一下空間複雜度為O(m+n)的思路(PS:該思路不符合題意的原地算法要求)。申請兩個一維數組,一個表示矩陣行,一個表示矩陣列。然後,遍歷矩陣中所有元素,一旦出現零,把該零對應行和對應列的一維數組的值標記為常數1。最後,分別按行和按列給原始矩陣賦值零。
現在參考LeetCode上一個評論的思路,空間複雜度為O(2)。申請兩個布爾變量cow和col,分別記錄原矩陣第0行和第0列中是否存在零,如果存在標記為True,否則標記為False。然後,接下來的思路就是上面O(m+n)的解決思路,唯一不同的是此時的空間是採用原始矩陣的空間。
具體代碼:
class Solution { public void setZeroes(int[][] matrix) { boolean row = false, col = false; for(int i = 0;i < matrix.length;i++) { if(matrix[i][0] == 0) { row = true; break; } } for(int j = 0;j < matrix[0].length;j++) { if(matrix[0][j] == 0) { col = true; break; } } for(int i = 1;i < matrix.length;i++) { for(int j = 1;j < matrix[0].length;j++) { if(matrix[i][j] == 0) { matrix[i][0] = 0; matrix[0][j] = 0; } } } for(int i = 1;i < matrix.length;i++) { if(matrix[i][0] == 0) { for(int j = 1;j < matrix[0].length;j++) matrix[i][j] = 0; } } for(int j = 1;j < matrix[0].length;j++) { if(matrix[0][j] == 0) { for(int i = 1;i < matrix.length;i++) matrix[i][j] = 0; } } if(row) { for(int i = 0;i < matrix.length;i++) matrix[i][0] = 0; } if(col) { for(int j = 0;j < matrix[0].length;j++) matrix[0][j] = 0; } } }
執行結果:

例5 生命遊戲
題號:289,難度:中等
題目描述:

解題思路:
此題在要求採用原地算法,即不能應用額外的空間來更新原始的矩陣元素。此題的解決方案需要使用位運算來解決。
先觀察題目對活細胞和死細胞的定義,然後把它們轉化為二進制表示。
活細胞:1變換為二進制01,如果活細胞變為死細胞,只需要把01變為11,即1變為3,其最後一位依然可以識別為活細胞。
死細胞:0變換為二進制00,如果死細胞變為活細胞,只需要把00變為10,即0變為2,其最後一位依然可以識別為死細胞。
最後,採用board[i][j]&1進行位運算的法則來求取一個細胞周圍的活細胞數量,並更新當前細胞的狀態。
具體代碼:
class Solution { public void gameOfLife(int[][] board) { // 01表示活細胞,01——>11變為死細胞,即由1變為3 // 00表示死細胞,00——>10變為活細胞,即由0變為2 for(int i = 0;i < board.length;i++) { for(int j = 0;j < board[0].length;j++) { int count = countLive(board, i, j); if((board[i][j] & 1) == 1) { if(count < 2 || count > 3) board[i][j] = 3; } else { if(count == 3) board[i][j] = 2; } } } for(int i = 0;i < board.length;i++) { for(int j = 0;j < board[0].length;j++) { if(board[i][j] == 3) board[i][j] = 0; if(board[i][j] == 2) board[i][j] = 1; } } } public int countLive(int[][] board, int x, int y) { int[][] step = {{-1, -1}, {-1, 0}, {-1, 1}, {0, -1}, {0, 1}, {1, -1}, {1, 0}, {1, 1}}; int count = 0; for(int i = 0;i < step.length;i++) { int temp_x = x + step[i][0]; int temp_y = y + step[i][1]; if(temp_x >= 0 && temp_x < board.length && temp_y >= 0 && temp_y < board[0].length) { if((board[temp_x][temp_y] & 1) == 1) count++; } } return count; } }
執行結果:

例6 圖像重疊
題號:835,難度:中等
題目描述:

解題思路:
此題注意如何處理矩陣的移動,使得移動後兩個矩陣進行匹配。直接採用兩個for循環表示其中一個矩陣移動後的位置。具體變換形式參考代碼。
具體代碼:
class Solution { public int largestOverlap(int[][] A, int[][] B) { int result = 0, len = A.length; for(int i = 0;i < len;i++) { for(int j = 0;j < len;j++) { int count1 = 0, count2 = 0; for(int m = 0;m < len - i;m++) { for(int n = 0;n < len - j;n++) { count1 += (A[m][n] & B[m+i][n+j]); count2 += (B[m][n] & A[m+i][n+j]); } } result = Math.max(result, count1); result = Math.max(result, count2); } } return result; } }
執行結果:

例7 車的可用捕獲量
題號:999,難度:簡單
題目描述:

解題思路:
本題較為簡單,直接遍歷矩陣找到車的位置,然後在車能行走的四個方向依次遍歷即可。(放入此題的意圖,題目比較長,讀懂題意需要耗費一些時間,另外編寫代碼需要注意邊界問題)
具體代碼:
class Solution { public int numRookCaptures(char[][] board) { for(int i = 0;i < board.length;i++) { for(int j = 0;j < board[0].length;j++) { if(board[i][j] == 'R') return getResult(board, i, j); } } return 0; } public int getResult(char[][] board, int x, int y) { int count = 0; int tempX = x, tempY = y; //向上 while(--tempX >= 0) { if(board[tempX][y] == 'B') break; else if(board[tempX][y] == 'p') { count++; break; } } tempX = x; //向下 while(++tempX < board.length) { if(board[tempX][y] == 'B') break; else if(board[tempX][y] == 'p') { count++; break; } } //向左 while(--tempY >= 0) { if(board[x][tempY] == 'B') break; else if(board[x][tempY] == 'p') { count++; break; } } tempY = y; //向右 while(++tempY < board[0].length) { if(board[x][tempY] == 'B') break; else if(board[x][tempY] == 'p') { count++; break; } } return count; } }
執行結果:

例8 可以攻擊國王的皇后
題號:1222,難度:中等
題目描述:
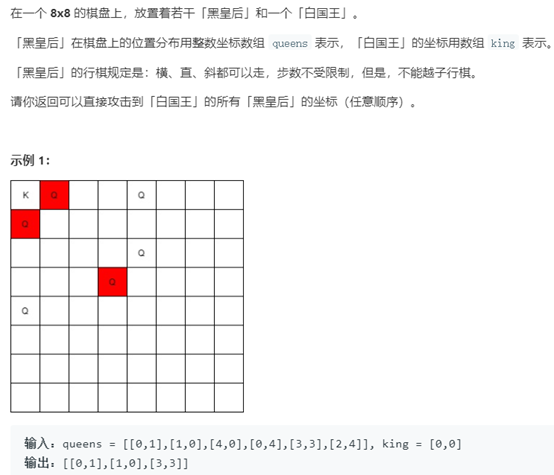
解題思路:
此題是例7的一個小小的升級版,重點還是處理邊界問題,以及快速編寫代碼和一次通過的能力。
具體代碼:
class Solution { private int[][] used; public List<List<Integer>> queensAttacktheKing(int[][] queens, int[] king) { used = new int[8][8]; used[king[0]][king[1]] = 2; for(int i = 0;i < queens.length;i++) used[queens[i][0]][queens[i][1]] = 1; List<List<Integer>> result = new ArrayList<>(); for(int i = 0;i < queens.length;i++) { if(judgeQ(queens[i][0], queens[i][1])) { List<Integer> temp = new ArrayList<>(); temp.add(queens[i][0]); temp.add(queens[i][1]); result.add(temp); } } return result; } public boolean judgeQ(int x, int y) { int x1 = x; while(--x1 >= 0) { if(used[x1][y] == 2) return true; if(used[x1][y] == 1) break; } int x2 = x; while(++x2 < 8) { if(used[x2][y] == 2) return true; if(used[x2][y] == 1) break; } int y1 = y; while(--y1 >= 0) { if(used[x][y1] == 2) return true; if(used[x][y1] == 1) break; } int y2 = y; while(++y2 < 8) { if(used[x][y2] == 2) return true; if(used[x][y2] == 1) break; } int x3 = x, y3 = y; while(--x3 >= 0 && --y3 >= 0) { if(used[x3][y3] == 2) return true; if(used[x3][y3] == 1) break; } int x4 = x, y4 = y; while(++x4 < 8 && ++y4 < 8) { if(used[x4][y4] == 2) return true; if(used[x4][y4] == 1) break; } int x5 = x, y5 = y; while(--x5 >= 0 && ++y5 < 8) { if(used[x5][y5] == 2) return true; if(used[x5][y5] == 1) break; } int x6 = x, y6 = y; while(++x6 < 8 && --y6 >= 0) { if(used[x6][y6] == 2) return true; if(used[x6][y6] == 1) break; } return false; } }
執行結果:

例9 搜索二維矩陣
題號:74,難度:中等
題目描述:

解題思路:
正常的想法是把矩陣想像成一個一維數組,然後採用二分查找的思路來實現。但是,這種方法可能需要處理(1,m)和(m,1)這兩種特殊的二維矩陣邊界問題(PS:在LeetCode上看到過直接應用二分查找很快解決的代碼)。因為矩陣按照行是有序的,不妨採用每行最後一個值作為邊界與目標值進行比較大小,每次增加一行或者減少一列的數據,具體實現可參考代碼。
具體代碼:
class Solution { /* 二分查找的代碼 public boolean searchMatrix(int[][] matrix, int target) { if (matrix.length == 0 || matrix[0].length == 0) return false; int begin, mid, end; begin = mid = 0; int len1 = matrix.length, len2 = matrix[0].length; end = len1 * len2 - 1; while (begin < end) { mid = (begin + end) / 2; if (matrix[mid / len2][mid % len2] < target) begin = mid + 1; else end = mid; } return matrix[begin / len2][begin % len2] == target; } */ public boolean searchMatrix(int[][] matrix, int target) { if(matrix.length == 0) return false; int row = 0, col = matrix[0].length-1; while(row < matrix.length && col >= 0){ if(matrix[row][col] < target) row++; else if(matrix[row][col] > target) col--; else return true; } return false; } }
執行結果:

例10 最小路徑和
題號:64,難度:中等
題目描述:

解題思路:
此題最直接的思路是採用遞歸進行深度搜索遍歷來解決,但是提交代碼後發現會出現超時的問題。此時,需要考慮應用動態規劃的思想來解題。動態規劃的轉換方程:dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j],另外需要考慮矩陣邊界的問題。
具體代碼:
class Solution { public int minPathSum(int[][] grid) { int[][] dp = new int[grid.length + 1][grid[0].length + 1]; for(int i = 1;i < dp.length;i++) { for(int j = 1;j < dp[0].length;j++) { if(i == 1) dp[i][j] = dp[i][j-1] + grid[i-1][j-1]; else if(j == 1) dp[i][j] = dp[i-1][j] + grid[i-1][j-1]; else dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + grid[i-1][j-1]; } } return dp[grid.length][grid[0].length]; } }
執行結果:

例11 元素和為目標值的子矩陣數量
題號:1074,難度:困難
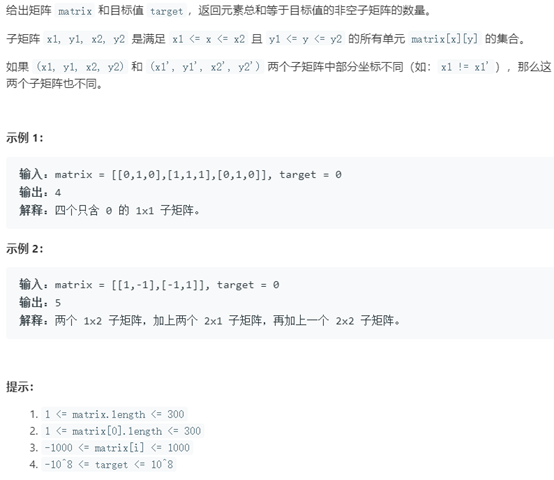
題目描述:
解題思路:
這道題其實是《和為K的子數組,題號:560,難度:中等》的一個升級版,560題是一維數組,本題是二維數組,其和變成了一個子矩陣的形式。此處我們可以採用把矩陣每行的元素變換成從該行開始道當前元素的和,另外單獨選兩列求矩陣和,這樣就把二維數組變成了列形式的一維數組求和。此時,解題思路就和560題一樣。
具體代碼:
class Solution { public int numSubmatrixSumTarget(int[][] matrix, int target) { for(int i = 0;i < matrix.length;i++) for(int j = 1;j < matrix[0].length;j++) matrix[i][j] += matrix[i][j-1]; int result = 0; for(int j1 = 0;j1 < matrix[0].length;j1++) { for(int j2 = j1;j2 < matrix[0].length;j2++) { Map<Integer, Integer> map = new HashMap<>(); map.put(0,1); int pre = 0; for(int i = 0;i < matrix.length;i++) { int val = pre + (j1 == 0 ? matrix[i][j2] : matrix[i][j2] - matrix[i][j1-1]); result += map.getOrDefault(val - target, 0); map.put(val, map.getOrDefault(val, 0)+1); pre = val; } } } return result; } }
執行結果:

例12 變為棋盤
題號:782,難度:困難
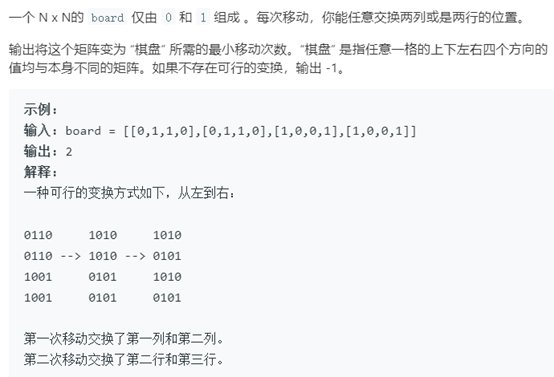
題目描述:
解題思路:
本題分析一下01出現的規律,可知如果n為偶數,那麼每行每列中0和1的個數必然相等;如果n為奇數,那麼0和1個數差的絕對值為1。由於矩陣只能交換行和列,結果要出現0和1不斷相間排列,那麼所有行中只能出現兩種模式的01排列方式,並且這兩種排列方式互補。例如,n=4, 第一行排序:1001,那麼其他行要不等於1001,要麼等於0110,否則就不可能轉換為棋盤,直接輸出-1即可。對於列的情況,和行一樣。(PS:此題需要處理最小變換次數的邊界問題,分奇偶討論行或者列的最小交換次數)
具體代碼:
class Solution { public int movesToChessboard(int[][] board) { if(check(board)) { int row = 0, start = board[0][0]; for(int i = 1;i < board.length;i++) { if(board[i][0] == start) row++; start = 1 - start; } int col = 0; start = board[0][0]; for(int j = 1;j < board[0].length;j++) { if(board[0][j] == start) col++; start = 1 - start; } if(board.length % 2 == 0) { // 分奇數偶數討論行和列最小交換次數 row = Math.min(board.length-row, row); col = Math.min(board.length-col, col); } else { if(row % 2 == 1) row = board.length-row; if(col % 2 == 1) col = board.length-col; } return row / 2 + col / 2; } return -1; } public boolean judgeEqual(int[][] board, int i, int j) { for(int k = 0;k < board[0].length;k++) { if(board[i][k] != board[j][k]) return false; } return true; } public boolean judgeNotEqual(int[][] board, int i, int j) { for(int k = 0;k < board[0].length;k++) { if(board[i][k] == board[j][k]) return false; } return true; } public boolean check(int[][] board) { int row_0 = 0, row_1 = 0, col_0 = 0, col_1 = 0; for(int i = 0;i < board[0].length;i++) { if(board[0][i] == 0) row_0++; else if(board[0][i] == 1) row_1++; if(board[i][0] == 0) col_0++; else if(board[i][0] == 1) col_1++; } if(Math.abs(row_0 - row_1) > 1 || row_0+row_1 != board[0].length) return false; if(Math.abs(col_0 - col_1) > 1 || col_0+col_1 != board.length) return false; row_0 = 0; row_1 = 0; for(int j = 1;j < board[0].length;j++) { if(judgeEqual(board, 0, j)) row_0++; else if(judgeNotEqual(board, 0, j)) row_1++; else return false; } return true; } }
執行結果: