前言

前面介紹學習的大多是線性表相關的內容，把指針搞懂後其實也沒有什麼難度。規則相對是簡單的。

再數據結構中樹、圖才是數據結構標誌性產物，(線性表大多都現成api可以使用),因為樹的難度相比線性表大一些並且樹的拓展性很強，你所知道的樹、二叉樹、二叉排序樹，AVL樹，線索二叉樹、紅黑樹、B數、線段樹等等高級數據結構。然而二叉排序樹是所有的基礎，所以徹底搞懂二叉排序樹也是非常重要的。

樹

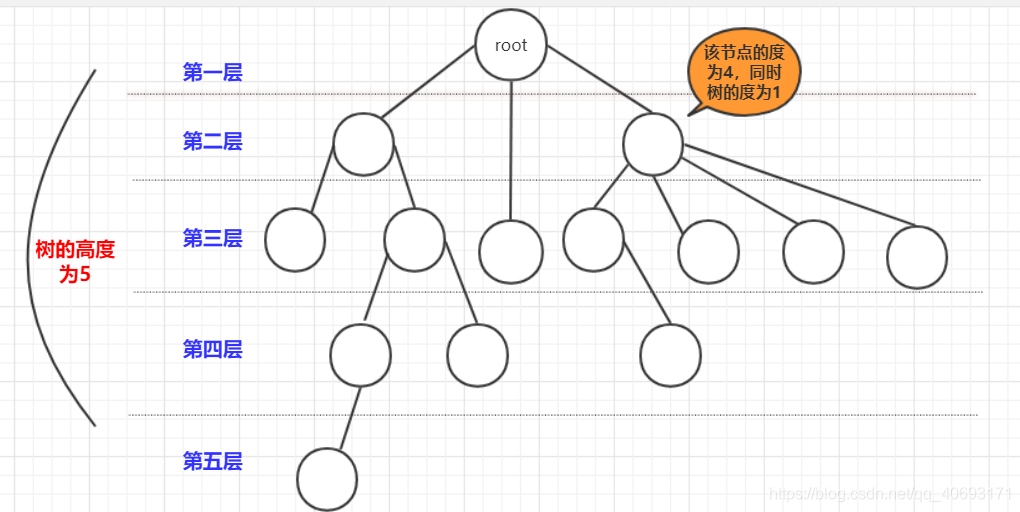
參考王道數據結構

二叉樹也是樹的一種，而二叉排序樹又是二叉樹的一種。

• 樹是遞歸的，將樹的任何一個節點以及節點下的節點都能組合成一個新的樹。並且很多操作基於遞歸完成。
• 根節點： 最上面的那個節點(root)，根節點沒有前驅節點，只有子節點（0個或多個都可以）
• 層數： 一般認為根節點是第1層(有的也說第0層)。而樹的高度就是層數最高(上圖層數開始為1)節點的層數
• 節點關係: 父節點：就是鏈接該節點的上一層節點,孩子節點:和父節點對應，上下關係。而祖先節點是父節點的父節點(或者祖先）節點。兄弟節點：擁有同一個父節點的節點們！
• 度： 節點的度就是節點擁有孩子節點的個數(是孩子不是子孫).而樹的度(最大)節點的度。同時，如果度大於0就成為分支節點,度等於0就成為葉子節點（沒有子孫）。

相關性質：

• 樹的節點數=所有節點度數+1.
• 度為m的樹第i層最多有mi-1個節點。(i>=1)
• 高度而h的m叉樹最多（mh-1）/(m-1)個節點(等比數列求和)
• n個節點的m叉樹最小高度[logm(n(m-1)+1)]

二叉樹

二叉樹是一樹的一種，但應用比較多，所以需要深入學習。二叉樹的每個節點最多只有兩個節點。

二叉樹與度為2的樹的區別：

• 一：度為2的的樹必須有三個節點以上，二叉樹可以為空。
• 二：二叉樹的度不一定為2：比如說斜樹。
• 三：二叉樹有左右節點區分，而度為2的樹沒有左右節點的區分。

幾種特殊二叉樹：

• 滿二叉樹。高度為n的滿二叉樹有2n-1個節點
  
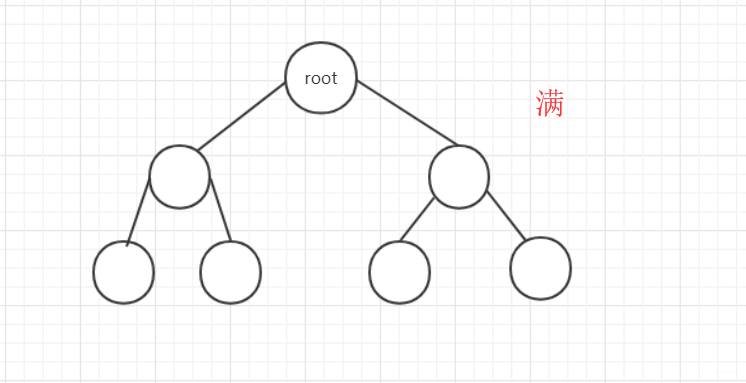
• 完全二叉樹：上面一層全部滿，最下一層從左到右順序排列
  
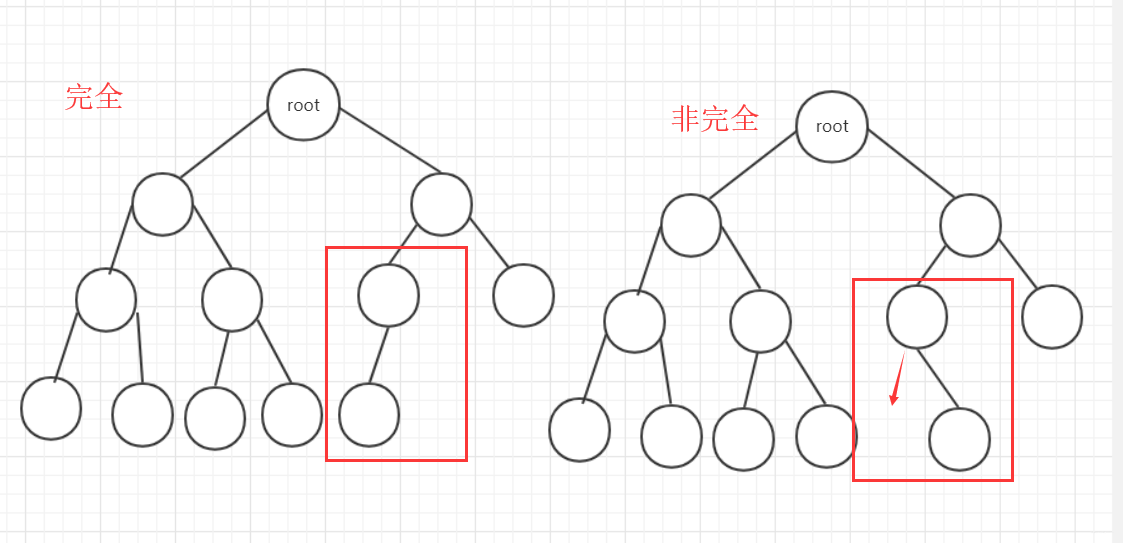
• 二叉排序樹：樹按照一定規則插入排序(本文詳解)。
• 平衡二叉樹：樹上任意節點左子樹和右子樹深度差距不超過1.

二叉樹性質：
相比樹，二叉樹的性質就是樹的性質更加具體化。

• 非空二叉樹葉子節點數=度為2的節點樹+1.本來一個節點如果度為1.那麼一直延續就一個葉子，但如果出現一個度為2除了延續原來的一個節點，會多出一個節點需要維繫。所以到最後會多出一個葉子。
• 非空第i層最多有2i-1個節點。
• 高為h的樹最多有2h-1個節點(等比求和)。
• 完全二叉樹若從左往右，從上到下編號如圖：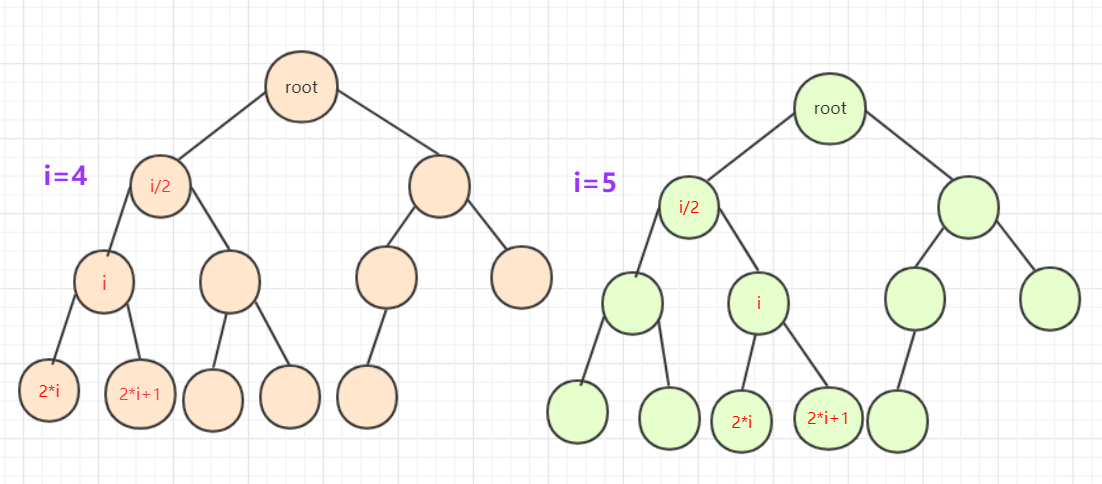
  

二叉排序(搜索)樹

概念

前面鋪墊那麼多，咱們言歸正傳，詳細實現一個二叉排序樹。首先要了解二叉排序樹的規則：

• 從任意節點開始，節點左側節點值總比節點右側值要小。
  例如。一個二叉排序樹依次插入15，6，23，7，4，71，5，50會形成下圖順序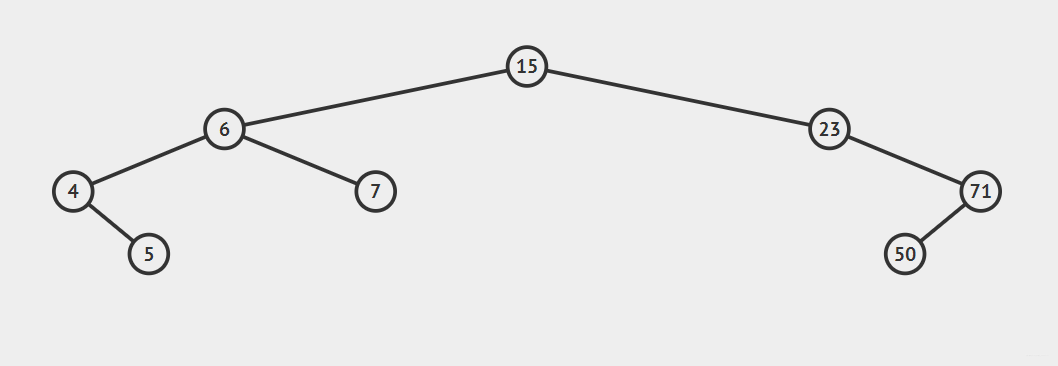
  

構造

首先二叉排序樹是由若干節點構成。

• 對於node需要這些屬性：left，right，和value。其中left和right是左右指針，而value是儲存的數據，這裡用int 類型。

node類構造為：

class node {//結點  	public int value;  	public node left;  	public node right;  	public node()  	{  	}  	public node(int value)  	{  		this.value=value;  		this.left=null;  		this.right=null;  	}  	public node(int value,node l,node r)  	{  		this.value=value;  		this.left=l;  		this.right=r;  	}  }  

既然節點構造好了，那麼就需要節點等其他信息構造成樹。有了鏈表構造經驗，很容易得知一棵樹最主要的還是root根節點。
所以樹的構造為：

public class BinarySortTree {  	node root;//根  	public BinarySortTree()  	{root=null;}  	public void makeEmpty()//變空  	{root=null;}  	public boolean isEmpty()//查看是否為空  	{return root==null;}  	//各種方法  }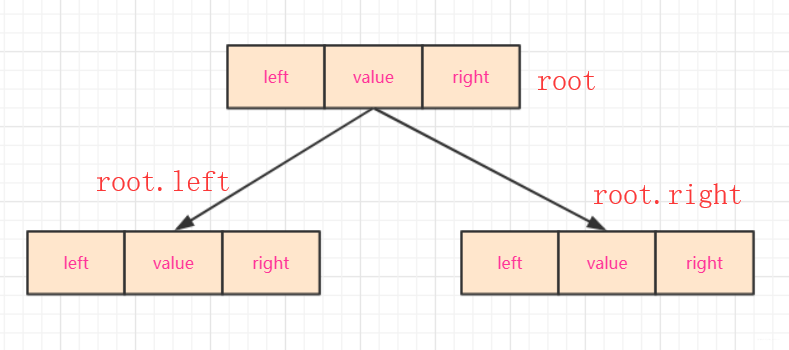  

主要方法

• 既然已經構造號一棵樹，那麼就需要實現主要的方法。因為二叉排序樹中每個節點都能看作一棵樹。所以我們創建方法的是時候加上節點參數(也就是函數對每一個節點都能有效)

findmax(),findmin()

findmin()找到最小節點：

• 因為所有節點的最小都是往左插入，所以只需要找到最左側的返回即可。

findmax()找到最大節點：

• 因為所有節點大的都是往右面插入，所以只需要找到最右側的返回即可。
  代碼使用遞歸函數

public node findmin(node t)//查找最小返回值是node，調用查看結果時需要.value  {  	if(t==null) {return null;}  	else if(t.left==null) {return t;}  	else return(findmin(t.left));  }  public node findmax(node t)//查找最大  {  	if(t==null) {return null;}  	else if(t.right==null) {return t;}  	else return(findmax(t.right));  }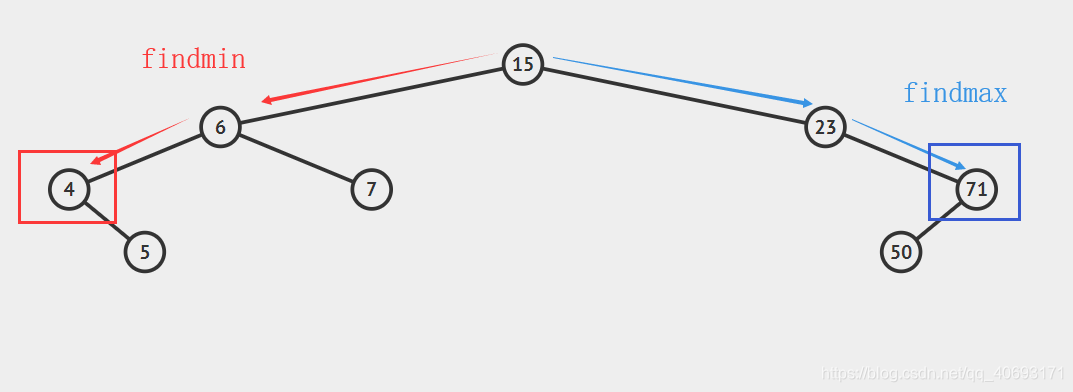  

isContains(int x)

這裡的意思是查找二叉查找樹中是否存在x。

• 假設我們我們插入x，那麼如果存在x我們一定會在查找插入路徑的過程中遇到x。因為你可以如果已經存在的點，再它的前方會走一次和它相同的步驟。也就是說前面固定，我來1w次x，那麼x都會到達這個位置。那麼我們直接進行查找比較即可！

public boolean isContains(int x)//是否存在  {  	node current=root;  	if(root==null) {return false;}  	while(current.value!=x&&current!=null)  	{  		if(x<current.value) {current=current.left;}  		if(x>current.value) {current=current.right;}  		if(current==null) {return false;}//在裏面判斷如果超直接返回  	}  	//如果在這個位置判斷是否為空會導致current.value不存在報錯  	 if(current.value==x) {return true;}  	return false;  }  

insert(int x)

插入的思想和前面isContains類似。找到自己的位置(空位置)插入。但是又不太一樣。你可能會疑問為什麼不直接找到最後一個空，然後將current賦值過去current=new node(x)。這樣的化current就相當於指向一個new node(x)節點。和樹就脫離關係，所以要提前判定是否為空，若為空將它的left或者right賦值即可。

public node insert(int x)// 插入 t是root的引用  {  	node current = root;  	if (root == null) {  		root = new node(x);  		return root;  	}  	while (current != null) {  		if (x < current.value) {  			if (current.left == null) {  				return current.left = new node(x);}  			else current = current.left;}  	    else if (x > current.value) {  			if (current.right == null) {  				return current.right = new node(x);}  			else current = current.right;  		}  	}  	return current;//其中用不到  }  

• 比如說上面結構插入51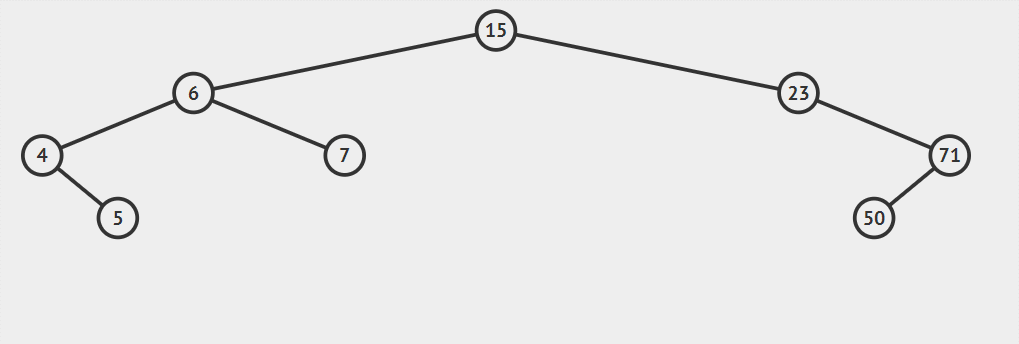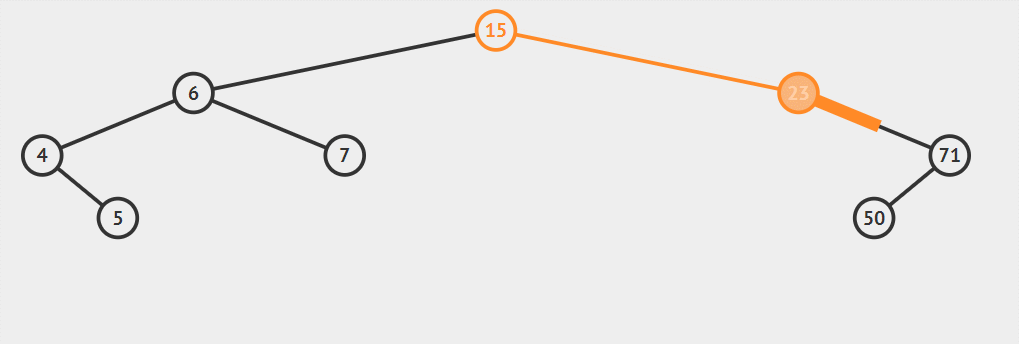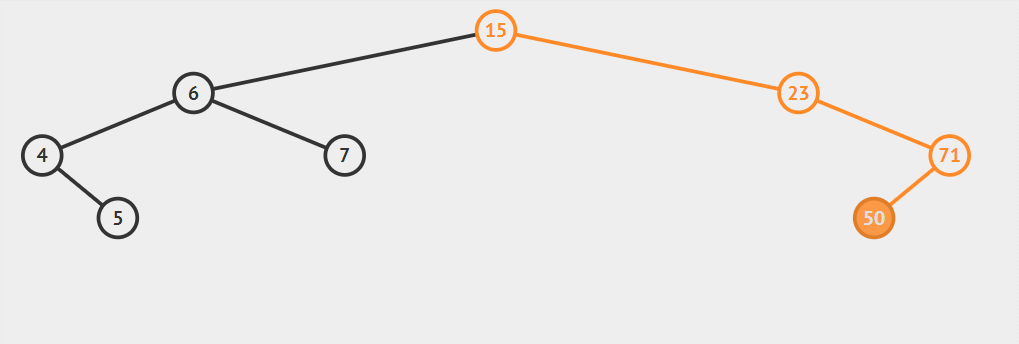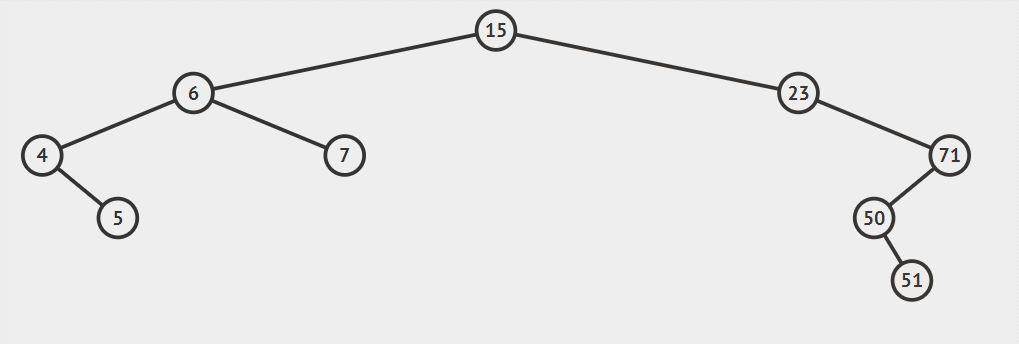
  

delete(int x)

刪除操作算是一個相對較難理解的操作了。
刪除節點規則：

• 先找到這個點。這個點用這個點的子樹可以補上的點填充該點，然後在以這個點為頭刪除替代的子節點（調用遞歸）然後在添加到最後情況（只有一個分支，等等）。
• 首先要找到移除的位置，然後移除的那個點分類討論，如果有兩個兒子，就選右邊兒子的最左側那個點替代，然後再子樹刪除替代的那個點。如果是一個節點，判斷是左空還是右空，將這個點指向不空的那個。不空的那個就替代了這個節點。入股左右都是空，那麼他自己變空null就刪除了。

刪除的節點沒有子孫:

• 這種情況不需要考慮，直接刪除即可。(途中紅色點)。另節點=null即可。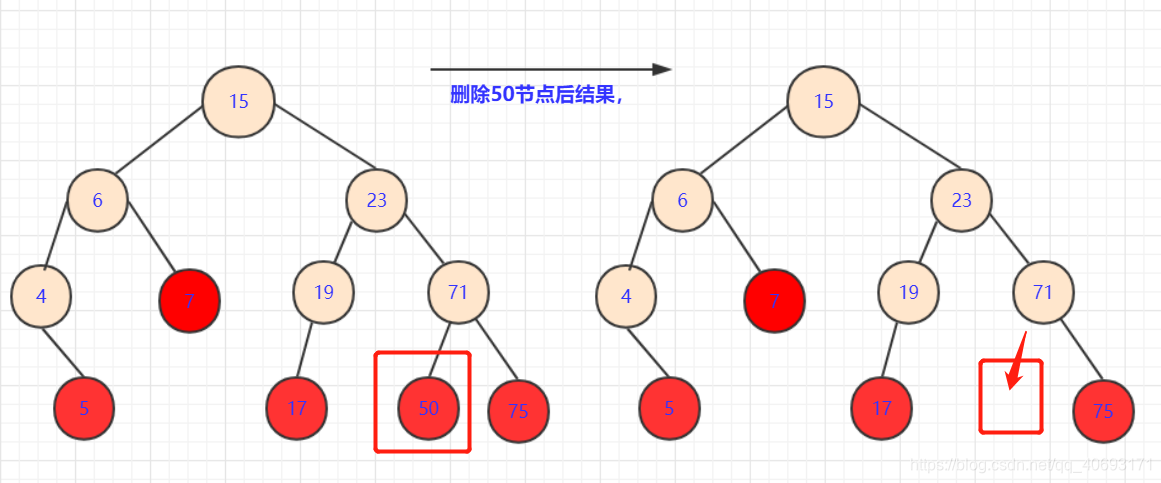
  

左節點為空、右節點為空：

• 此種情況也很容易，直接將刪除點的子節點放到被刪除位置即可。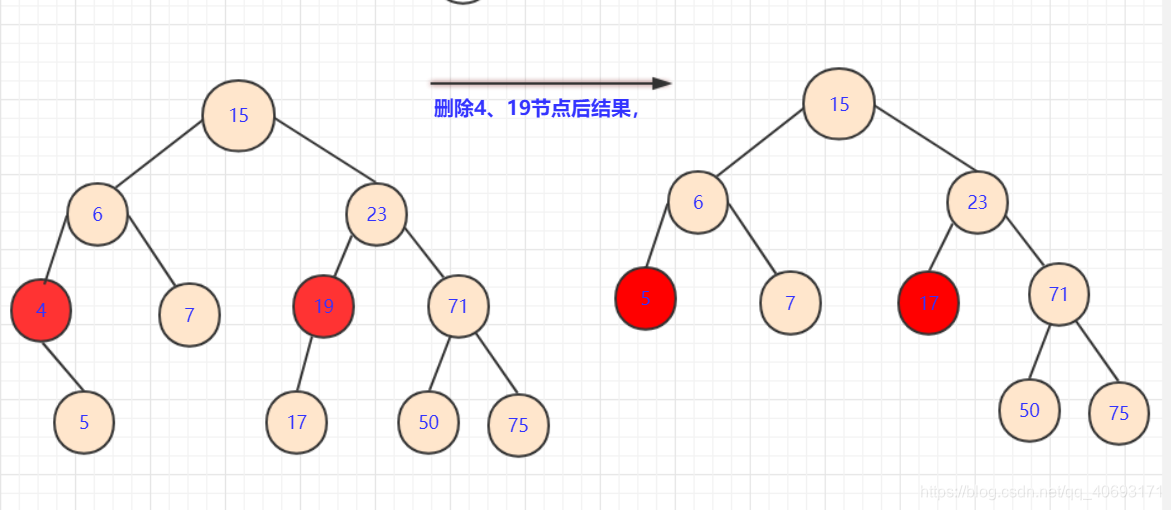
  

左右節點均不空

• 這種情況相對是複雜的。因為這涉及到一個策略問題。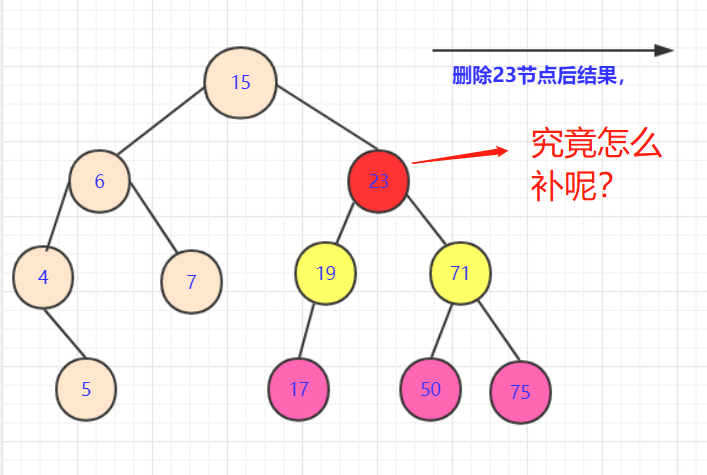
  
• 如果拿19或者71節點填補。雖然可以保證部分側大於小於該節點，但是會引起合併的混亂.比如你若用71替代23節點。那麼你需要考慮三個節點(19,50,75)之間如何處理，還要考慮他們是否滿，是否有子女。這是個極其複雜的過程。
• 首先，我們要分析我們要的這個點的屬性：能夠繼承被刪除點的所有屬性。如果取左側節點(例如17)那麼首先能滿足所有右側節點都比他大（右側比左側大）。那麼就要再這邊選一個最大的點讓左半枝都比它小。我們分析左支最大的點一定是子樹最右側！
• 如果這個節點是最底層我們很好考慮，可以直接替換值，然後將最底層的點刪除即可。但是如果這個節點有左枝。我們該怎麼辦？
• 這個分析起來也不難，用遞歸的思想啊。我們刪除這個節點，用可以滿足的節點替換了。會產生什麼樣的後果？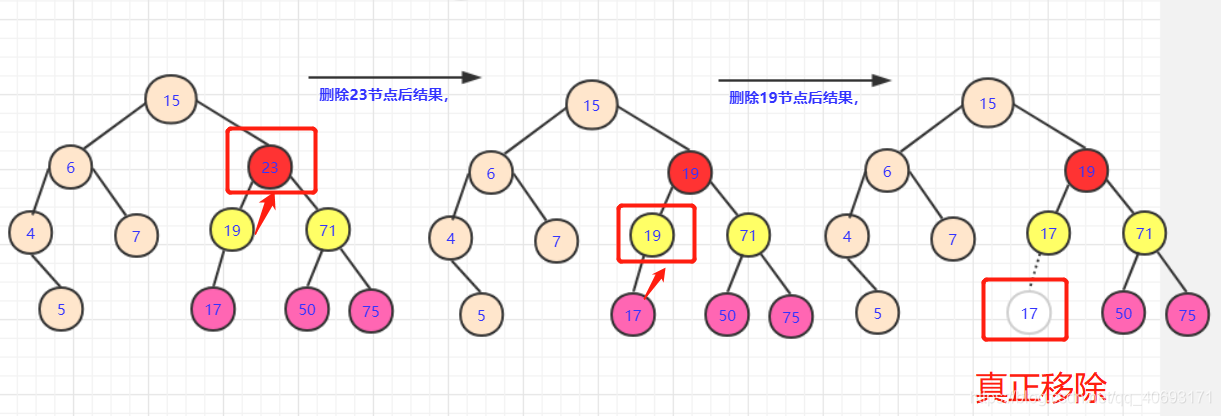
  
• 多出個用過的19節點，轉化一下，在左子樹中刪除19的點！那麼這個問題又轉化為刪除節點的問題，查找左子樹中有沒有能夠替代19這個點的。

所以整個刪除算法流程為：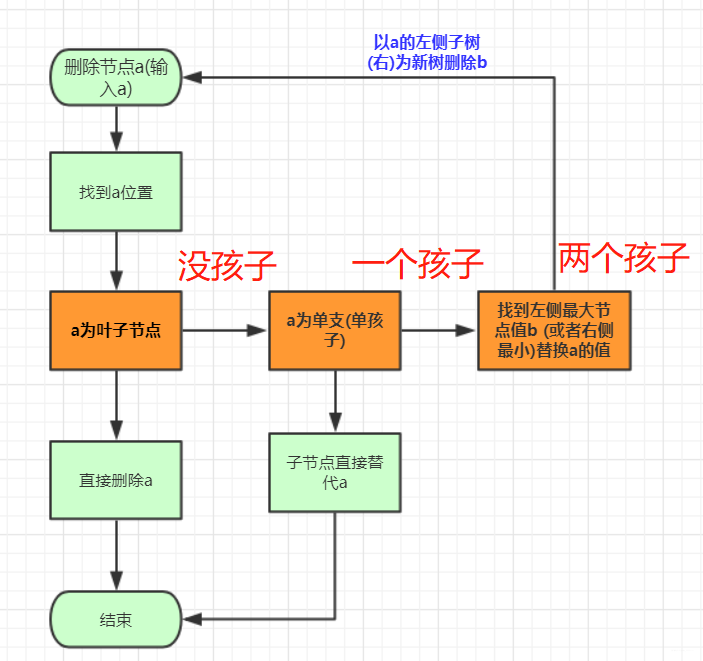

代碼為

public node remove(int x, node t)// 刪除節點  	{  		if (t == null) {  			return null;  		}  		if (x < t.value) {  			t.left = remove(x, t.left);  		} else if (x > t.value) {  			t.right = remove(x, t.right);  		} else if (t.left != null && t.right != null)// 左右節點均不空  		{  			t.value = findmin(t.right).value;// 找到右側最小值替代  			t.right = remove(t.value, t.right);  		} else // 左右單空或者左右都空  		{  			if (t.left == null && t.right == null) {  				t = null;  			} else if (t.right != null) {  				t = t.right;  			} else if (t.left != null) {  				t = t.left;  			}  			return t;  		}  		return t;  	}  

完整代碼

二叉排序樹完整代碼為：

package 二叉樹;    import java.util.ArrayDeque;  import java.util.Queue;  import java.util.Stack;    public class BinarySortTree {  	class node {// 結點  		public int value;  		public node left;  		public node right;    		public node() {  		}    		public node(int value) {  			this.value = value;  			this.left = null;  			this.right = null;  		}    		public node(int value, node l, node r) {  			this.value = value;  			this.left = l;  			this.right = r;  		}  	}    	node root;// 根    	public BinarySortTree() {  		root = null;  	}    	public void makeEmpty()// 變空  	{  		root = null;  	}    	public boolean isEmpty()// 查看是否為空  	{  		return root == null;  	}    	public node findmin(node t)// 查找最小返回值是node，調用查看結果時需要.value  	{  		if (t == null) {  			return null;  		} else if (t.left == null) {  			return t;  		} else  			return (findmin(t.left));  	}    	public node findmax(node t)// 查找最大  	{  		if (t == null) {  			return null;  		} else if (t.right == null) {  			return t;  		} else  			return (findmax(t.right));  	}    	public boolean isContains(int x)// 是否存在  	{  		node current = root;  		if (root == null) {  			return false;  		}  		while (current.value != x && current != null) {  			if (x < current.value) {  				current = current.left;  			}  			if (x > current.value) {  				current = current.right;  			}  			if (current == null) {  				return false;  			} // 在裏面判斷如果超直接返回  		}  		// 如果在這個位置判斷是否為空會導致current.value不存在報錯  		if (current.value == x) {  			return true;  		}  		return false;  	}    	public node insert(int x)// 插入 t是root的引用  	{  		node current = root;  		if (root == null) {  			root = new node(x);  			return root;  		}  		while (current != null) {  			if (x < current.value) {  				if (current.left == null) {  					return current.left = new node(x);}  				else current = current.left;}  		    else if (x > current.value) {  				if (current.right == null) {  					return current.right = new node(x);}  				else current = current.right;  			}  		}  		return current;//其中用不到  	}    	public node remove(int x, node t)// 刪除節點  	{  		if (t == null) {  			return null;  		}  		if (x < t.value) {  			t.left = remove(x, t.left);  		} else if (x > t.value) {  			t.right = remove(x, t.right);  		} else if (t.left != null && t.right != null)// 左右節點均不空  		{  			t.value = findmin(t.right).value;// 找到右側最小值替代  			t.right = remove(t.value, t.right);  		} else // 左右單空或者左右都空  		{  			if (t.left == null && t.right == null) {  				t = null;  			} else if (t.right != null) {  				t = t.right;  			} else if (t.left != null) {  				t = t.left;  			}  			return t;  		}  		return t;  	}  }  

結語

• 這裡我們優先學習了樹，二叉樹，以及二叉搜素樹的基本構造。對於二叉搜素樹插入查找比較容易理解但是實現的時候要注意函數對參數的引用等等。需要認真考慮。
• 而偏有難度的是二叉樹的刪除，利用一個遞歸的思想，要找到特殊情況和普通情況，遞歸一定程度也是問題的轉化(轉成自己相同問題，作用域減小)需要思考。
• 下面還會介紹二叉搜素樹的三序遍歷(遞歸和非遞歸).和層序遍歷。需要的朋友請持續關注。另外，筆者數據結構專欄歡迎查房。！
• 如果對後端、爬蟲、數據結構算法等感性趣歡迎關注我的個人公眾號交流：bigsai。回復爬蟲，數據結構等有精美資料一份。