半監督學習（五）——半監督支持向量機

• 2019 年 11 月 1 日
• 筆記

半監督支持向量機（S3VMs）

　　今天我們主要介紹SVM分類器以及它的半監督形式S3VM，到這裡我們關於半監督學習基礎算法的介紹暫時告一段落了。之後小編還會以論文分享的形式介紹一些比較新的半監督學習算法。讓我們開始今天的學習吧~

引入

　　支持向量機（SVM）相信大家並不陌生吧？但是如果數據集中有大量無標籤數據（如下圖b），那麼決策邊界應該如何去確定呢？僅使用有標籤數據學得的決策邊界（如下圖a）將穿過密集的無標籤數據，如果我們假定兩個類是完全分開的，那麼該決策邊界並不是我們想要的，我們希望的決策邊界是下圖（b）中的黑色實線。

　　新的決策邊界可以很好地將無標籤數據分成兩類，而且也正確地分類了有標籤數據（雖然它到最近的有標籤數據的距離比SVM小）。

支持向量機SVM

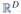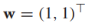　　首先我們來討論SVMs，為我們接下來要介紹的S3VMs算法做鋪墊。為了簡單起見，我們討論二分類問題，即y{-1,1}，特徵空間為並定義決策邊界如下其中w是決定決策邊界方向和尺度的參數向量，b是偏移量。舉個例子，，b=-1，決策邊界就如下圖藍色線所示，決策邊界總是垂直於w向量。

　　我們的模型為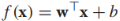，決策邊界是f(x)=0，我們通過sign(f(x))來預測x的標籤，我們感興趣的是實例x到決策邊界的距離，該距離的絕對值為，比如原點x=(0,0)到決策邊界的距離為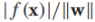，如上圖中的綠色實線。我們定義有標籤實例到決策邊界的有符號距離為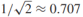。假設訓練數據是線性可分的（至少存在一條線性決策邊界正確分類所有的標籤數據）。有符號的決策邊距是決策邊界到距離它最近的有標籤數據的距離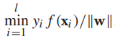：，如果一個決策邊界能分離有標籤訓練樣本，幾何邊界是正的，我們通過尋找最大幾何邊距來發現決策邊界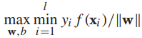：，這個式子很難直接優化，所以我們將它重寫為等價形式。首先我們注意到參數（w,b）可以任意縮放為（cw, cb）,所以我們要求最接近決策邊界的實例滿足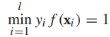：，接下來，目標方程可以重寫為約束優化問題的形式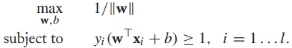：，而且，最大化1/||w||相當於最小化||w||的平方：

 　　到目前為止，我們都是基於訓練樣本是線性可分的，現在我們放寬這個條件，那麼上述目標方程不再滿足。我們要對約束條件進行鬆弛使得在某些實例上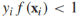，同時對這些鬆弛進行懲罰，重寫目標方程為：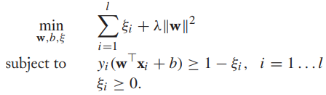

 　　然而，將目標函數轉換成一個正則化的風險最小化的形式是有必要的（這關係到我們將其拓展到S3VMs）。考慮這樣一個優化問題：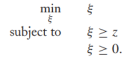

 　　很容易可以看出當z<=0時，目標函數值為0，否則為z，所以可以簡寫為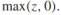

 　　注意（*）中的約束條件可以重寫為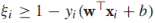，利用剛才的結論，我們將（*）重寫為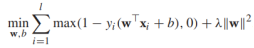

 　　其中第一項代表的是hinge loss損失函數，第二項是正則項。

　　我們這裡不再深入討論SVMs的對偶形式或者核技巧（將特徵映射到更高維度的空間來解決非線性問題），雖然這兩個問題是SVMs的關鍵，但不是我們要介紹的S3VMs的重點（當然也可以將核技巧直接應用到S3VMs上），感興趣的同學可以去看相關的論文。

半監督支持向量機（S3VMs）

　　在上文中我們提到用hinge loss來使有標籤數據分類儘可能正確，但是如果存在無標籤數據呢？沒有標籤的話就不能知道是否分類正確，就更別提懲罰了。

　　我們已經學習出來一個標籤預測器sign(f(x))，對於無標籤樣本，它的預測標籤為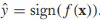，我們假定該預測值就是x的標籤，那麼就可以在x上應用hinge損失函數了

 　　我們稱它為hat loss。

　　由於我們標籤就是用f(x)生成的，無標籤樣本總是能被正確分類，然而hat loss 仍然可以懲罰一定的無標籤樣本。從式子中可以看出，hat損失函數更偏愛（懲罰為0，離決策邊界比較遠），而懲罰-1<f(x)<1（特別是趨近於0）的樣本，因為這些樣本很有可能被分類錯誤，現在，我們可以寫出S3VMs的在有標籤和無標籤數據上的目標方程：（**）

　　其實我們可以看出來S3VMs的目標方程偏向於將無標籤數據儘可能遠離決策邊界（也就是說，決策邊界儘可能穿過無標籤數據的低密度區域（是不是像聚類算法的作用））。其實上面的目標方程更像是 正則化的風險最小化形式（在有標籤數據上使用hinge loss），其正則化項為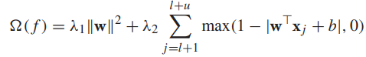

　　還需要注意的一點是，從經驗上來看，（**）的結果是不平衡的（大多數甚至所有的無標籤數據可能被分為一個類），造成這種現象的原因雖然還不清楚，為了修正這種錯誤，一種啟發式方法就是在無標籤數據上限制預測類的比例與標籤數據的比例相同，由於是不連續的，所以這個約束很難滿足，所以我們對其進行鬆弛，轉化為包含連續函數的約束：，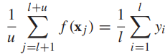

完整的S3VMs的目標函數可以寫作：

　　然而，S3VMs算法的目標函數不是凸的，也就是說，他有多個局部優解，這是我們求解目標函數的一個計算難點。學習算法可能會陷入一個次優的局部最優解，而不是全局最優解，S3VMs的一個研究熱點就是有效的找到一個近似最優解。

熵正則化

　　SVMs和S3VMs 不是概率模型，也就是說他們不是通過計算類的後驗概率來進行分類的。在統計機器學習中，有很多概率模型是通過計算p(y|x)來進行分類的，有趣的是對於這些概率模型也有一個對S3VMs的直接模擬，叫做entropy regularization。為了使我們的討論更加具體，我們將首先介紹一個特定的概率模型：邏輯回歸，並通過熵正則將它擴展到半監督學習上。

邏輯回歸對類的後驗概率進行建模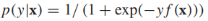，將f(x)的範圍從規約到[0,1]，模型的參數是w和b。給定有標籤的訓練樣本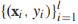條件對數似然是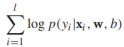，假定w服從高斯分佈，I是對角矩陣，那麼邏輯回歸模型的訓練就是最大化後驗概率：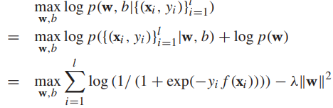

 　　這相當於下面的正則化風險最小化問題：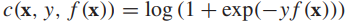

 　　邏輯回歸沒有使用無標籤數據，我們可以加入無標籤數據，基於如下準則：如果兩個類可以很好的分開，那麼在任何無標籤樣本上的分類都是可信的：要麼屬於正類要麼屬於負類。同樣，後驗概率要麼接近於1，要麼接近於0.一種度量置信度的方法就是熵，對於概率為p的伯努利隨機變量，熵的定義如下：

 　　給定無標籤樣本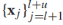，可以定義邏輯回歸的熵正則化器為：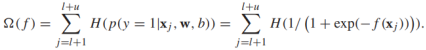

 　　如果未標記實例的分類是確定的，則該值較小。直接將它應用到S3VMs上，我們可以定義半監督的邏輯回歸模型：

 The assumption of S3VMs

　　S3VMs和熵正則的假設就是樣本的類可以很好的分開，決策邊界落在樣本特徵空間的低密度區域且不會通過密集的未標記數據。如果這個假設不滿足，S3VMs可能會導致很差的表現。

小結：

　　今天我們介紹了SVM分類器以及它的半監督形式S3VM，與我們前面討論的半監督學習技術不同，S3VMs尋找一個在無標籤數據的低密度區間的決策邊界。我們還介紹了熵正則化，它是基於邏輯回歸的概念模型的。到這裡我們關於半監督學習基礎算法的介紹暫時告一段落了。之後還會以論文分享的形式介紹一些比較新的半監督學習算法。後面的內容會探索人類和機器學習的半監督學習之間的聯繫，並討論半監督學習研究對認知科學領域的潛在影響，敬請期待~！

希望大家多多支持我的公眾號，掃碼關注，我們一起學習，一起進步~