JS數據結構第五篇 — 二叉樹和二叉查找樹
- 2019 年 10 月 3 日
- 筆記
一、二叉樹的基本概念
從邏輯結構角度來看,前面說的鏈表、棧、隊列都是線性結構;而今天要了解的“二叉樹”屬於樹形結構。
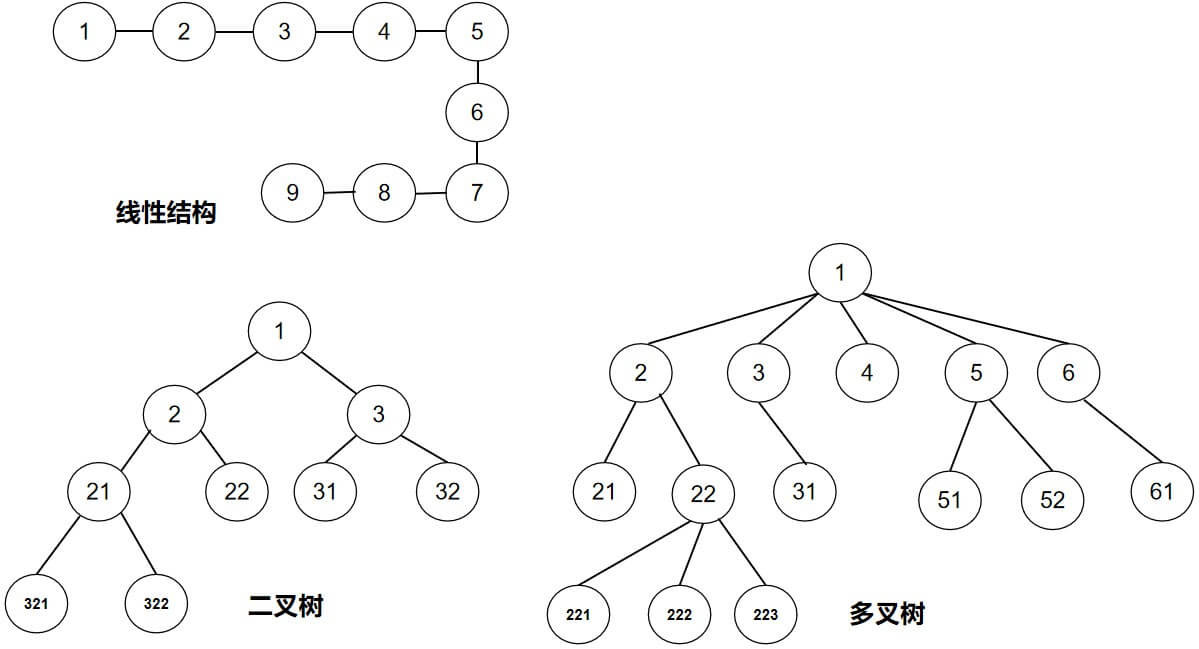
1.1 多叉樹的基本概念,以上圖中“多叉樹”為例說明
節點:多叉樹中的每一個點都叫節點;其中最上面的那個節點叫“根節點”;
父節點:節點1是節點2/3/4/5/6的父節點,然後節點2/3/4/5/6是節點1的子節點;節點2/3/4/5/6又是互為兄弟節點,因為它們有父節點為同一個節點;
空樹:一個沒有任何節點的樹叫空樹;一棵樹可以只有一個節點,也就是只有根節點;
子樹:子節點及子節點的後台節點形成的一個節點集合叫子樹;對於只有兩個子節點的節點,其左邊的子節點叫左子樹,右邊的叫右子樹;
葉子節點(leaf):子樹為0的節點;其他子樹不為0的節點叫“非葉子節點”;
層數(level):根節點在第1層,根節點的子節點在第2層,以此類推(有些說法也從第0層開始結算);
節點的深度(depth):從根節點到當前節點的唯一路徑上的節點總數;
節點的高度(height):從當前節點到最遠葉子節點的路徑上的節點總數;
樹的深度:所有節點深度中的最大值;
樹的高度:所以節點高度中的最大值;數的深度等於數的高度
有序樹:樹中任意節點的子節點之間有順序關係;
無序樹:樹中任意節點的子節點之間沒有順序關係,也叫“自由樹”;
森林:由n(n >= 0) 顆不相交的樹組成的集合;
1.2 二叉樹的特點
- 每個節點的度最大為2(最多擁有2顆子樹);
- 左子樹和右子樹是有順序的。即使某節點只有一顆子樹,也要區分左右子樹;
- 非空二叉樹的第i層,最多有2^(i-1)個節點(i >= 1)
- 在高度為h的二叉樹上最多有2^h – 1個節點(h >= 1);
- 對於任何一顆非空二叉樹,如果葉子節點個數為n0, 度為2的節點個數為n2, 則有n0 = n2 + 1。(這個好理解,假如這個二叉樹除了第一級節點有2個子節點,後面的節點都是只有一個子節點,則不管這顆二叉樹如何往下延伸,永遠度為2的節點個數是1個,葉子節點為2個;然後如果在這個二叉樹的中間節點,每加一個節點,相當於度為2的節點加一個,葉子節點也加一個,則度為2的節點和葉子節點的增加是同步同數量的,所以對於二叉樹,葉子節點個數 = 度為2的節點個數 + 1 公式是永遠成立的)
- 假設度為1的節點個數為n1, 那麼二叉樹的節點總數 n = n0 + n1 + n2。則二叉樹的邊數T = n1 + 2 * n2 = n -1 = n0 + n1 + n2 -1 –> n2 + 1 = n0
1.3 真二叉樹/滿二叉樹/完全二叉樹
- 真二叉樹:所有節點的度都要麼為2,要麼為0;
- 滿二叉樹:所有節點的度都要麼為2,要麼為0,且所有的葉子節點都在最後一層;
- 假設滿二叉樹的高度為h (h>=1),那麼第i層的節點數量:2^(i-1), 葉子節點數量:2(^h-1), 總節點數量n = 2^h -1 = 2^0 + 2^1 + 2^2 + … + 2^(h-1)
- 等比數列公式:a1=1, 公比q=2, 則an = a1*q^(n-1)=2^(n-1), 前n項之和Sn = a1+a2+…+an = 2^0 + 2^1 + 2^2 + … + 2^(n-1) = a1(1-q^n)/(1-q)=2^n-1
- 在同樣高度的二叉樹中,滿二叉樹的葉子節點數量最多、總節點數量最多;
- 滿二叉樹一定是真二叉樹,真二叉樹不一定是滿二叉樹;
- 完全二叉樹:葉子節點只會出現在最後兩層,且最後一層的葉子節點都靠左對齊;
- 完全二叉樹從根節點到倒數第二層是一顆滿二叉樹;滿二叉一定是完全二叉樹,完全二叉樹不一定是滿二叉樹;
- 度為1的節點只有左子樹;度為1的節點要麼是1個,要麼是0個;
- 假設完全二叉樹的高度為h(h>=1), 那麼至少有2^(h-1) 個節點(2^0 + 2^1 + 2^2 + … + 2^(h-2) + 1), 最多有2^h – 1個節點(2^0 + 2^1 + 2^2 + …+ 2^(h-1), 滿二叉樹);總節點數量為n, 則有2^(h-1) <= n < 2^h –> h-1 <= log(2)(n) < h –> h = floor(log(2)(n)) + 1 (floor是向下取整,ceiling是向上取整)
- 一顆有n個節點的完全二叉樹(n > 0),從上到下,從左到右對節點從1開始進行編號,對任意第i個節點
- 如果i = 1, 它是根節點
- 如果i > 1, 它的父節點編號為floor(i/2)
- 如果2i <= n, 它的左子節點編號為2i
- 如果2i > n, 它無左子節點
- 如果2i + 1 <= n, 它的右子節點編號為2i + 1
- 如果2i + 1 > n , 它無右子節點
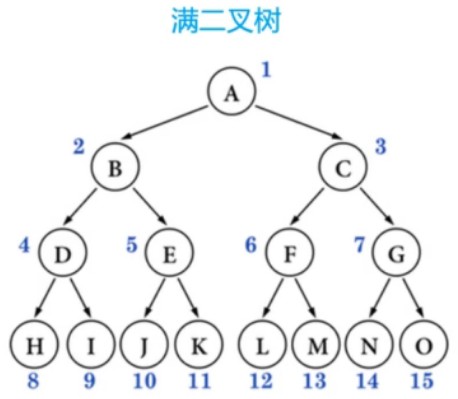

面試題:如果一顆完全二叉樹有768個節點,求葉子節點的個數?
分析:假設葉子節點個數為n0,度為1的節點個數為n1,度為2的節點個數為n2。
則總節點個數n = n0 + n1 + n2,而且n0 = n2 + 1 ;
則n = 2n0 + n1 -1
根據完全二叉樹的定義我們知道,n1要麼為0,要麼為1:
當n1為1時, n = 2n0, n必然為偶數。葉子節點個數n0 = n / 2,非葉子節點個數 n1 + n2 = n / 2 ;
當n1為0,n = 2n0 – 1,n必然為奇數。葉子節點個數n0 = (n + 1) / 2, 非葉子節點個數 n1 + n2 = (n – 1) / 2
因此可以判斷出來當這個完全二叉樹有768個節點時,它的葉子節點個數為:384
二、二叉查找樹
二叉查找樹是一種特殊的二叉樹,較小的值保存在左節點中,較大的值保存在右節點中。這一特性使得查找的效率很高,對於數值型和非數值型的數據,如單詞和字符串,都是如此。
2.1 二叉查找樹的插入邏輯
2.1.1 設根節點為當前節點
2.1.2 如果待插入節點保存的數據小於當前節點,則設新的當前節點為原節點的左節點;反之,執行第2.1.4步
2.1.3 如果當前節點的左節點為null, 就將新的節點插入這個位置,退出循環;反之,繼續執行下一次循環
2.1.4 設新的當前節點為原節點的右節點
2.1.5 如果當前節點的右節點為null, 就將新的節點插入這個位置,退出循環;反之,繼續執行下一次循環

//插入元素 function insertBST(element){ var node = new Node(element, null, null); //根節點判斷 if (root == null){ root = node; } else{ //非根節點 var current = root; while(true){ if (element < current.element){ //往左節點方向放 if (current.left == null){ current.left = node; break; } current = current.left; } else if (element > current.element){ //往右節點方向放 if (current.right == null){ current.right = node; break; } current = current.right; } else { //相等,替換 current.element = element; return; } } } size++; }
View Code
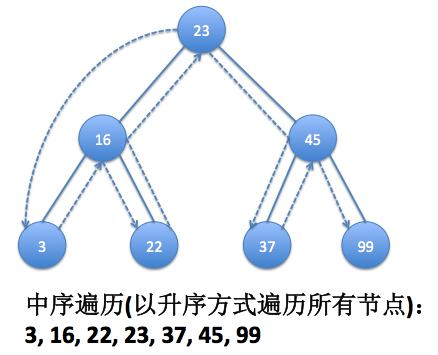
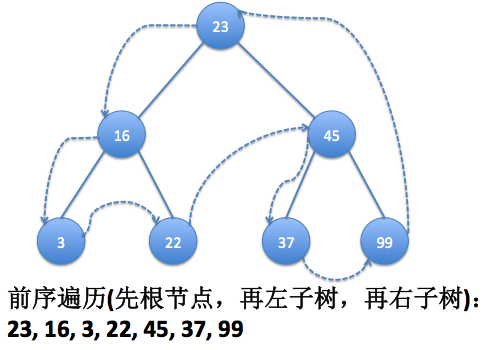
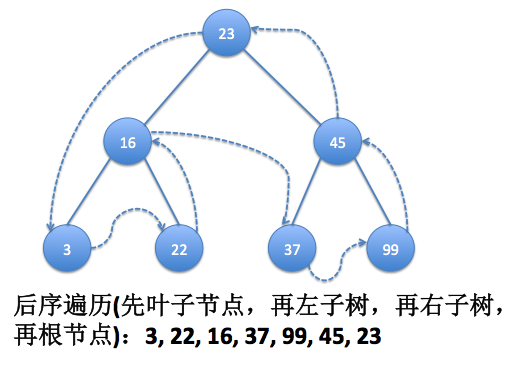
2.2 二叉查找樹的遍歷,遍歷有三種方式:中序、前序、後序
中序指以升序的方式遍歷所有節點;前序是指先訪問根節點,再以同樣的方式訪問左子樹和右子樹;後序指的是先訪問葉子節點,再從左子樹到右子樹,最後到根節點。
先看個效果圖
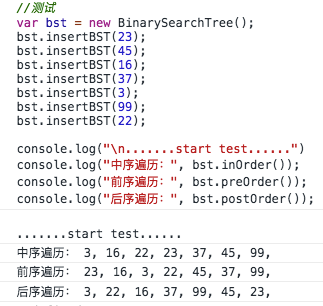
遍歷走勢分析圖:
遍歷代碼:

//二叉樹中序遍歷:以升序方式訪問二叉樹中所有節點 function inOrder(){ return inOrderByNode(root); } function inOrderByNode(node){ if (node){ var str = ""; str += inOrderByNode(node.left); str += node.element + ", "; str += inOrderByNode(node.right); return str; } return ""; } //前序遍歷:先訪問根節點,再訪問左子樹和右子樹 function preOrder(){ return preOrderByNode(root); } function preOrderByNode(node){ if (node){ var str = ''; str += node.element + ", "; //先訪問根節點 str += preOrderByNode(node.left); //再訪問左子樹 str += preOrderByNode(node.right); //再訪問右子樹 return str; } return ""; } //後序遍歷:先訪問葉子節點,再左子樹,再右子樹,再到根節點 function postOrder(){ return postOrderByNode(root); } function postOrderByNode(node){ if (node){ var str = ""; str += postOrderByNode(node.left); str += postOrderByNode(node.right); str += node.element + ", "; return str; } return ""; }
View Code
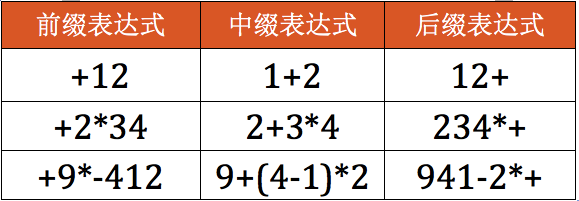
四則運算的表達式可以分為三種:
- 前綴表達式(prefix expression),又稱波蘭表達式
- 中綴表達式(infix expression)
- 後綴表達式(postfix expression),又稱為逆波蘭式表達式
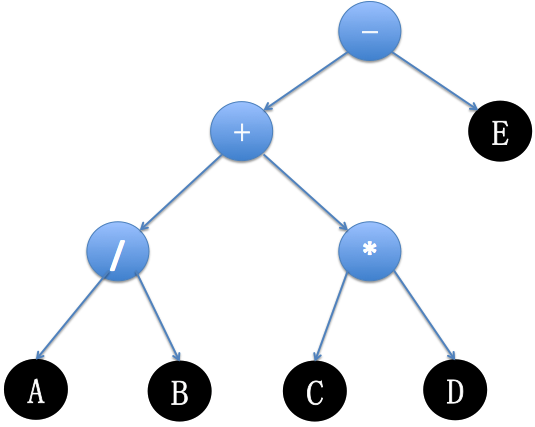
如果將表達式的操作作為葉子節點,運算符作為父節點(假設只有四則運算),這些節點剛好可以組成一顆二叉樹。
比如表達式:A / B + C * D – E ,如果對這顆二叉樹進行遍歷
- 前序遍歷:- + / A B * C D E ,剛好就是前綴表達式(波蘭表達式)
- 中序遍歷:A / B + C * D – E,剛好就是中綴表達式
- 後序遍歷:A B / C D * + E -,剛好就是後綴表達式(逆波蘭表達式)
2.3 查找二叉查找樹的最大值、最小值、是否存在某個值
最大值:因為較大的值都是在右子樹上,則最大值一定是在右子樹的最後一個節點上;
最小值:較小的值都是在左子樹上,則最小值一定在左子樹的最後一個節點上;
是否存在某個值,則是遍歷查找

//查找最小值:因為較小的值都在左邊,所以最小值一定是左子樹的最後一個節點 function getMin(){ var minNode = getMinNode(root); if (minNode) { return minNode.element; } return null; } //查找最小節點 function getMinNode(node){ var current = node; while(current){ if (current.left == null){ return current; } current = current.left; } return null; } //查找最大值:因為較大的值都在右邊,所以最大值一定是在右子樹的最後一個節點 function getMax(){ var maxNode = getMaxNode(root); if (maxNode){ return maxNode.element; } return null; } //查找最大節點 function getMaxNode(node){ var current = node; while(current){ if (current.right == null){ return current; } current = current.right; } return null; } //查找指定值,是否存在這個元素 function isExist(element){ var current = root; while(current){ if (element < current.element){ //左子樹尋找 current = current.left; } else if (element > current.element){ //右子樹尋找 current = current.right; } else{ //存在 return true; } } return false; }
View Code
2.4 刪除二叉查找樹中的指定元素
從二叉查找樹上刪除節點的操作最複雜,其複雜程度取決於刪除哪個節點。如果刪除沒有子節點 的節點,那麼非常簡單。如果節點只有一個子節點,不管是左子節點還是右子節點,就變 得稍微有點複雜了。刪除包含兩個子節點的節點最複雜。

//刪除元素 function remove(element){ root = removeNode(root, element); } function removeNode(node, element){ if (node == null) { return null; } if (node.element == element){ size--; //node沒有左子樹 if (node.left == null){ return node.right; } else if (node.right == null){ //node沒有右子樹 return node.left; } /** * node有左子樹和右子樹,這個時候要找出最接近node節點值的節點 * 1、如果找出比node節點的element稍大的節點,則從node右節點的最小節點 * 2、如果找出比node節點的element稍小的節點,則從node左節點的最大節點 */ //第一種方式,找出比node的element稍微大點的節點 var minNode = getMinNode(node.right); node.element = minNode.element; node.right = removeNode(node.right, minNode.element); // //第二種方式, 找出比node的element稍微小點的節點 // var maxNode = getMaxNode(node.left); // node.element = maxNode.element; // node.left = removeNode(node.left, maxNode.element); return node; } else if(element < node.element){ //往左子樹方向繼續找 node.left = removeNode(node.left, element); return node; } else{ //往右子樹方向繼續找 node.right = removeNode(node.right, element); return node; } }
View Code

