NVDLA中Winograd卷積的設計
- 2019 年 10 月 30 日
- 筆記
在AI芯片:高性能卷積計算中的數據復用曾提到,基於變換域的卷積計算——譬如Winograd卷積——並不能適應算法上對卷積計算多變的需求。但Winograd卷積依舊出現在剛剛公開的ARM Ethos-N57和Ethos-N37 NPUs的支持特性中,本文將利用Nvidia開源的NVIDIA Deep Learning Accelerator (NVDLA)為例,分析在硬件中支持Winograd卷積的實現方式,代價和收益;以期對基於變換域卷積的優勢和不足有更深的認識。
1. Windgrad卷積的計算方式
卷積神經網絡中的三維卷積(後文簡稱為卷積)計算過程可以表示如下,將這種直接通過原始定義計算卷積的方式稱為直接卷積(Direct Convolution)。
for i = 1 : Ho for j = 1 : Wo for k = 1 : Co for l = 1 : R for m = 1 : S for n = 1 : Ci out[i,j,k] += In[i*s+l.j*s+m,n]*F[l,m,n];其中各參數的含義如下表
| 數據維度 | 描述 |
|---|---|
| Ho/Wo | 輸出feature map的高和寬 |
| Co | 輸出的channel數目 |
| R/S | filter的高和寬 |
| Ci | 輸入的channel數目 |
| s | 卷積計算的stride |
和一般的乘加運算不同,卷積計算中有滑窗的過程,充分利用這一點特性可以節約計算過程中的乘法次數。關於Winograd的原理和推導,可以參考https://blog.csdn.net/antkillerfarm/article/details/78769624中的相關內容。此處直接給出3×3, stride=1卷積下Winograd卷積的形式(參見NVDLA Unit)。
[S = A^Tleft[left(GgG^Tright) odot left( C^TdC right) right]A ]
[ g = begin{bmatrix} wt_{0,0} & wt_{0,1} & wt_{0,2} \ wt_{1,0} & wt_{1,1} & wt_{1,2} \ wt_{2,0} & wt_{2,1} & wt_{2,2} end{bmatrix} ]
[d = begin{bmatrix} x_{0,0} & x_{0,1} & x_{0,2} & x_{0,3}\ x_{1,0} & x_{1,1} & x_{1,2} & x_{1,3}\ x_{2,0} & x_{2,1} & x_{2,2} & x_{2,3}\ x_{3,0} & x_{3,1} & x_{3,2} & x_{3,3} end{bmatrix} ]
[C = begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & -1 & 1 \ -1& 1 & 1 & 0 \ 0 & 0 & 0 & -1 end{bmatrix} ]
[G = begin{bmatrix} 1 & 0 & 0 \ 0.5 & 0.5 & 0.5 \ 0.5 & -0.5& 0.5 \ 0 & 0 & 1 end{bmatrix} ]
[A_T = begin{bmatrix} 1 & 1 & 1 & 0 \ 0 & 1 &-1 &-1 end{bmatrix} ]
其中(g)是3×3的kernel,(d)是4×4的feature map,(odot)表示矩陣對應位置元素相乘。(s)表示2×2的卷積結果。矩陣(C), (G), (A)為常量,用於Wingrad卷積中的變換。由於(C), (G), (A)中各元素取值為(pm1,pm0.5), 因此計算可以通過加減和簡單移位得到,認為不需要進行乘法運算。
因此,採用Winograd卷積計算得到4哥輸出結果需要16次乘法計算,而直接卷積需要36次乘法計算。但是由於Winograd在變換中加入了加法計算,因此加法次數會有一定增加。注意上述討論中並沒有加入Channel方向,這是因為此處卷積在Channel上實際上依舊退化成了簡單的乘加運算,因此無論在變換前後進行Channel方向計算均沒有區別。
一段直接卷積和Winograd卷積對比的代碼如下所示
import numpy as np g = np.random.randint(-128,127,(3,3)) d = np.random.randint(-128,127,(4,4)) direct_conv = np.zeros((2,2)) for i in range(2): for j in range(2): for r in range(3): for s in range(3): direct_conv[i,j] = direct_conv[i,j] + d[i+r,j+s]*g[r,s] C = np.array([[1,0,0,0],[0,1,-1,1],[-1,1,1,0],[0,0,0,-1]]) G = np.array([[1,0,0],[0.5,0.5,0.5],[0.5,-0.5,0.5],[0,0,1]]) AT = np.array([[1,1,1,0],[0,1,-1,-1]]) U = G.dot(g).dot(G.transpose()) V = C.transpose().dot(d).dot(C) wg_conv = AT.dot(U*V).dot(AT.transpose()) print(direct_conv) print(wg_conv)由計算結果可知,兩者結果完全一致(如果採用浮點數時可能會有量化誤差,但都在合理範圍內)
>>> print(direct_conv) [[-23640. -51.] [-10740. 8740.]] >>> print(wg_conv) [[-23640. -51.] [-10740. 8740.]]2. NVDLA中的的直接卷積
在硬件設計過程中不可能為直接卷積和Winograd卷積分別設計完全獨立的計算和控制邏輯,由於直接卷積有計算靈活和適應性強的特點,各類神經網絡加速器都有支持。因此,Winograd一定是建立在直接卷積硬件結構基礎上的拓展功能。在探究NVDLA中的Winograd卷積設計之前,必須先明確NVDLA中的的直接卷積的計算方式。
Nvidia的相關文檔中十分詳細的NVDLA計算直接卷積的流程(NVDLA Unit),其將卷積計算分成了五級(下述描述中,以數值精度為Int16為例)
- Atomic Operation (原子操作,完成16次64次乘法並將其加在一起)
- Stripe Operation (條帶操作,完成16次獨立的Atomic Operation)
- Block Operation (塊操作,完成kernel的R/S方向的累加)
- Channel Operation(通道操作,完成Channel方向計算的累加)
- Group Operation (分組操作,完成一組kernel的全部計算)
NVDLA Unit中給出了可視化的圖像用於描述這個過程,這一過程實際上就是卷積的六層循環計算過程的拆解,可以表示如下
for k = 1 : Co/16 for i = 1 : Ho/4 // Group Operation for j = 1 : Wo/4 // Group Operation for n = 1 : Ci/64 // Channel Operation for l = 1 : R // Block Operation for m = 1 : S // Block Operation for ii = 1:4 // Strip Operation for ji = 1:4 // Strip Operation for ki = 1:16 // Antomic Operation for ni = 1:64 // Antomic Block out[i*4+ii,j*4+jj,k*16+ki] += In[(i*4+ii)*s+l.(j*4+jj)*s+m,n*64+ni]*F[l,m,n*64+ni];其中,Atomic Operation決定了NVDLA乘法陣列的設計。根據設計可以看出,NVDLA有16份完全一致的乘法陣列用於計算16個不同Kernel的乘法;而每個乘法陣列中有64個乘法和一棵64輸入的加法樹。
計算順序還一定程度確定了NVDLA的Buffer設計和數據路徑設計。在計算直接卷積時,每周期需要128Byte的Feature/Pixel數據,實際上時規則的64Channel的數據;因此在存儲時只需要每個Bank上存儲64Channel數據,使用時通過MUX選出指定Bank數據即可。在進行結果寫回時,每周期需要寫回16個Feature數據。由於Winograd卷積使用的Weight可以提前算好,對比直接卷積和Winograd卷積時可以忽略Weight路徑。
3. NVDLA中的Winograd卷積
建立在直接卷積的硬件架構上,NVDLA針對Winograd卷積進行了一系列的修改。從計算方式上來說,不再同時計算64個Channel的乘加;從硬件架構上來說,進行了計算修改和數據路徑修改。根據NVDLA的設計,Winograd卷積的計算(S = A^Tleft[left(GgG^Tright) odot left( C^TdC right) right]A) 實際上分佈在不同的階段/模塊進行。
- $U = GgG^T $是離線預先計算好的
- $V = C^TdC $是在數據路徑上計算的
- (S = A^Tleft[ Uodot Vright]A) 是在計算陣列中計算的
首先考慮計算陣列的設計。NVDLA計算3×3卷積,每次輸出2×2共計4個數,計算過程中有4×4的矩陣點乘計算;結合直接卷積中64個乘法計算,Winograd卷積同時計算了4個Channel,共計4x4x4=64次乘法。乘法計算本身沒有區別,但在進行加法時,和直接卷積略有不同,用代碼可表示為
//direct conv & winograd conv for i = 1:16 s1[i] = s0[i*4+0] + s0[i*4+1] + s0[i*4+2] + s0[i*4+3]; //direct conv for i = 1:8 s2[i] = s1[i*2+0] + s1[i*2+1]; for i = 1:4 s3[i] = s2[i*2+0] + s2[i*2+1]; s4[i] = s3[0] + s3[1] + s3[2] + s3[3]; //winograd conv for i=1:4 s2_wg[0][i] = s1[i*4+0] + s1[i*4+1] + s1[i*4+2]; s2_wg[0][i] = s1[i*4+1] - s1[i*4+2] + s1[i*4+3]; s3_wg[0][0] = s2_wg[0][0] + s2_wg[0][1] + s2_wg[0][2]; s3_wg[1][0] = s2_wg[1][0] + s2_wg[1][1] + s2_wg[1][2]; s3_wg[0][1] = s2_wg[0][1] - s2_wg[0][1] - s2_wg[0][2]; s3_wg[1][1] = s2_wg[1][1] - s2_wg[1][1] - s2_wg[1][2]; 代碼中只有第一級的加法被direct conv和winograd conv完全復用,其他級的加法略有不同。在NVDLA中,加法是使用Wallace Tree完成的,以提高性能降低資源佔用。Direct Conv中和Winograd Conv中的後面幾級加法還進行了進一步復用。總體來說,從代碼上看(參見NV_NVDLA_CMAC_CORE_mac.v),為了支持Winograd卷積
- 加法的第三級中增加了4棵4-2的Wallace Tree Compressor
- 加法的第四級中增加了2棵4-2的Wallace Tree Compressor
- 加法的第五級中增加了2棵6-2的Wallace Tree Compressor
- 增加了一些MUX以direct conv和winograd conv
其次考慮數據路徑,包括讀取的數據路徑和寫回的數據路徑。對於讀取而言,除了需要針對Winograd專門設計取址邏輯和數據選擇邏輯,還需要完成$V = C^TdC $的計算;根據文檔描述,這一計算過程是在PRA(Pre-addition)中完成的。從代碼上看(參見NV_NVDLA_CSC_dl.v)
- 針對Winograd的地址生成增加的控制邏輯可以忽略
- 針對Winograd的數據選擇增加數千的寄存器
- PRA採用MENTOR的HLS綜合工具實現,共實現了4份,和MAC陣列(1024乘加)對比,此處的計算資源較少
對於寫迴路徑而言,為了完成卷積計算,在乘加後增加了累加器和SRAM,其設計如下圖所示(ref. http://nvdla.org/_images/ias_image21_cacc.png)
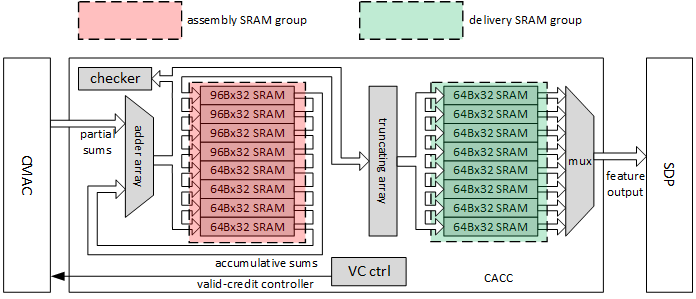
和Direct Conv一次輸出16個結果相比,Winograd Conv輸出的結果為64。這意味着為了支持Winograd Conv,需要額外增加48組高位寬的累加器。同時,SRAM的大小也需要設置為原先的四倍。
4. 相關討論
NVDLA為了同時支持Direct Conv和Winograd Conv顯然付出了一些代價。定性的分析來看,包括
- 4組PRA,每組PRA中約有8次加法
- 16棵加法樹,每棵增加了約8次加法
- 48組高位寬加法
- 增加了約25KB的Accumulator SRAM
而作為對比,一些典型數據包括
- MAC陣列中有1024次乘法和約1024次加法
- 用於存放Feature/Pixel/Weight的Buffer大小為512KB
顯然,為了支持Winograd Conv增加的資源並不會太多。當然,雖然讀取路徑和計算陣列的設計受Winograd Conv的影響不大;但是對於寫迴路徑而言,數據位寬發生了變化,一定程度影響了整體的架構設計。可能可以優化的地方包括將Direct Conv的輸出也改成2×2的大小,這樣寫回的數據路徑上Direct Conv和Winograd Conv就沒有差別了。
NVDLA是一個相對專用的加速器,從相關文檔中也可以看出,NVDLA專門針對計算中的各種特性/數據排列進行了硬件上的處理。而現有的很多加速器,為了兼顧不同網絡的計算效率,往往更為靈活。在這種情況下,Winograd Conv應該作為設計的可選項,這是因為
- 計算3×3卷積有2.25x的理論提升
- Winograd Conv的乘法依舊是矩陣計算
- Winograd Conv的數據路徑和直接卷積沒有必然的衝突
- Winograd Conv的加法可以直接在數據路徑上完成,甚至不影響其他設計
- 如果加速器設計粒度足夠細,甚至可以從軟件調度上直接支持Winograd Conv
完全不考慮Winograd Conv的理由只可能是未來算法發展趨勢下,3×3的普通卷積計算量佔比會大大下降。