Petya and Graph/最大權閉合子圖、最小割
原題地址：//codeforces.com/contest/1082/problem/G
2 seconds
256 megabytes
standard input
standard output
Petya has a simple graph (that is, a graph without loops or multiple edges) consisting of nn vertices and mm edges.
The weight of the ii-th vertex is aiai.
The weight of the ii-th edge is wiwi.
A subgraph of a graph is some set of the graph vertices and some set of the graph edges. The set of edges must meet the condition: both ends of each edge from the set must belong to the chosen set of vertices.
The weight of a subgraph is the sum of the weights of its edges, minus the sum of the weights of its vertices. You need to find the maximum weight of subgraph of given graph. The given graph does not contain loops and multiple edges.
The first line contains two numbers nn and mm (1≤n≤103,0≤m≤1031≤n≤103,0≤m≤103) – the number of vertices and edges in the graph, respectively.
The next line contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤1091≤ai≤109) – the weights of the vertices of the graph.
The following mm lines contain edges: the ii-e edge is defined by a triple of integers vi,ui,wivi,ui,wi (1≤vi,ui≤n,1≤wi≤109,vi≠ui1≤vi,ui≤n,1≤wi≤109,vi≠ui). This triple means that between the vertices vivi and uiui there is an edge of weight wiwi. It is guaranteed that the graph does not contain loops and multiple edges.
Print one integer — the maximum weight of the subgraph of the given graph.
4 5 1 5 2 2 1 3 4 1 4 4 3 4 5 3 2 2 4 2 2
8
3 3 9 7 8 1 2 1 2 3 2 1 3 3
0
In the first test example, the optimal subgraph consists of the vertices 1,3,41,3,4 and has weight 4+4+5−(1+2+2)=84+4+5−(1+2+2)=8. In the second test case, the optimal subgraph is empty.
題意：一個有n個點m條邊的圖，每個點有相應的點權值，邊有邊權值。讓你選擇一些邊，使得所選邊權值總和減去所選邊的端點的點權值總和的結果最大。
思路：
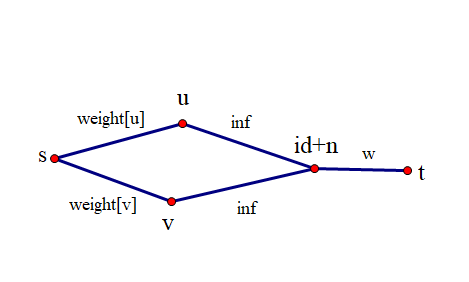
神奇網絡流，將源點s向所有點連邊，邊權為點的權值，對於每條邊，把它也看做一個點，並將它的兩個端點與它連邊，邊權為無窮大，再將他與匯點t連邊，邊權為原來的邊權。
設s、t為源點和匯點
對於邊（id，u，v, w）id表示第幾條邊，u、v表示它的兩個端點，w表示邊權,weight[u]表示點u的權值
add（s，u，weight[u]）,add（s，v，weight[v]）,add(u,id+n,inf), add(v,id+n,inf), add(id+n,t,w)（id+n是為了避免點和邊重合了）
對於一條邊，如果它的邊權大於他兩個端點的點權之和，那麼就要減去它的兩個端點點權之和，反之則捨棄掉這條邊。
所以答案就是所有邊的邊權之和減去最小割。
代碼：
#include<bits/stdc++.h>
#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define repp(i,a,b) for(int i=a;i<b;i++)
#define per(i,a,b) for(int i=a;i>=b;i--)
#define perr(i,a,b) for(int i=a;i>b;i--)
#define pb push_back
#define eb push_back
#define mst(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-12;
const double PI=acos(-1.0);
const double angcst=PI/180.0;
const ll mod=998244353;
ll max_3(ll a,ll b,ll c){if(a>b&&a>c)return a;if(b>c)return b;return c;}
ll min_3(ll a,ll b,ll c){if(a<b&&a<c)return a;if(b<c)return b;return c;}
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
ll qpow(ll a,ll n){ll r=1;while(n){if(n&1)r=(r*a)%mod;n>>=1;a=(a*a)%mod;}return r;}
ll qmul(ll a,ll b){ll s=(long double)a/mod*b;s=a*b-s*mod;if(s<0)s+=mod;if(s>=mod)s-=mod;return s;}
template <typename _Tp> inline _Tp read(_Tp&x){
char c11=getchar(),ob=0;x=0;
while(c11^'-'&&!isdigit(c11))c11=getchar();if(c11=='-')c11=getchar(),ob=1;
while(isdigit(c11))x=x*10+c11-'0',c11=getchar();if(ob)x=-x;return x;
}
int n,m;
const int maxn=200010;
struct edge
{
ll v,cost,rev;//邊的終點、邊權、反向邊
};
vector<edge>g[20*maxn];//vector存圖
ll deep[maxn];//表示源點到當前頂點的深度
ll iter[maxn];//當前弧，在其之前的邊已經沒有用了，避免了搜尋已經增廣過的路徑
void add(ll u,ll v,ll cost)//加邊
{
g[u].pb((edge){v,cost,g[v].size()});
g[v].pb((edge){u,0,g[u].size()-1});
}
void bfs(int s)//建立分層網絡，通過bfs計算從源點出發的距離標號
{
mst(deep,-1);
queue<int>q;
deep[s]=0;//源點深度為0
q.push(s);
while(!q.empty())
{
int v=q.front();q.pop();
for(int i=0;i<g[v].size();i++)
{
edge &e=g[v][i];
if(e.cost>0&&deep[e.v]==-1)//如果還有容量能夠到達i，並且i節點的深度未被標記
{
deep[e.v]=deep[v]+1;
q.push(e.v);
}
}
}
}
ll dfs(ll v,ll t,ll f)//基於分層網絡，通過dfs尋找增廣路,x表示當前節點，f表示當前這條增廣路徑上的最小流量
{
if(v==t)return f;//找到匯點，返回
for(ll &i=iter[v];i<g[v].size();i++)
{
edge &e=g[v][i];
if(e.cost>0&&deep[v]<deep[e.v])//找到能從v流通過去的相鄰頂點
{
ll d=dfs(e.v,t,min(f,e.cost));
if(d>0)
{
e.cost-=d;//更新殘餘網絡
g[e.v][e.rev].cost+=d;//反向邊
return d;
}
}
}
return 0;//搜不到增廣路徑就返回0
}
ll dinic(ll s,ll t)//求s到t的最大流
{
ll flow=0;
while(1)
{
bfs(s);
if(deep[t]<0)return flow;//不存在分層網絡，算法結束
mst(iter,0);
ll f;
while((f=dfs(s,t,INF))>0)
flow+=f;
}
}
int main()
{
ll sum=0;
read(n);read(m);
ll s=0,t=1+n+m,a;
rep(i,1,n)
{
read(a);
add(s,i,a);
}
rep(i,1,m)
{
ll u,v,w;
read(u);read(v);read(w);
add(u,i+n,LINF);
add(v,i+n,LINF);
add(i+n,t,w);
sum+=w;
}
printf("%lld\n",sum-dinic(s,t));
return 0;
}
