3.1 C語言_實現AVL平衡二叉樹
- 2019 年 10 月 25 日
- 筆記
【序】
上節我們實現了數據結構中最簡單的Vector,那麼來到第三章,我們需要實現一個Set
set的特點是 內部有序且有唯一元素值;同時各種操作的期望操作時間複雜度在O(n·logn);
那麼標準的C++ STL(Standard Template Library) 容器內部使用的是什麼呢?
STL使用的是紅黑樹或者hash Tree ,由於筆者現在的水平和精力,沒時間搞這個啦,於是我就
挑了一個稍微熟悉一點的數據結構:AVL 樹;
github:https://github.com/KimAlittleStar/cstd
【1.介紹】
AVL 樹是根據二叉查找樹改進延伸過來的,我們都知道二叉查找樹中只有一個規則,
那就是根節點的元素一定會大於左孩子,小於右孩子;如果是隨機數,那麼我們二叉查找樹的高度無限
接近於 logN(完全二叉樹)。但是由於其策略,在反覆的插入和刪除後,普通的二叉查找樹將會非常
偏科(偏向右子樹)如果樹的高度非常大(height == N) 那麼他和鏈表的操作時間沒有什麼區別,
為了避免普通二叉查找樹的缺陷,因此引申出 AVL Tree -> 平衡二叉查找樹;
AVL 和普通的二叉查找樹只有一個規則限制:相同節點的兩個孩子的高度最大相差為1,本身節點的高度
為兩個孩子節點中大的那個高度加1;
【2.基礎數據結構】
使用一個node 和 正常的tree 用於管理他的根和size;node 中有左孩子 右孩子和數據還有一個記錄樹的
高度位元組u8(unsigned char),為什麼我們使用u8,因為假設在滿足AVL的規則要求下,壞的情況樹的深度為
deep = logn *2 +1 ; 去除一個起始位0 ,後期可能會用到的錯誤位 -1,那麼在最差的情況下 u8 類型的高度可以存儲
大概多少個節點呢:
N = 2^254 (個)而我們在tree 中 size 的類型是 u32 (unsigned int)完全夠用了;
參考下圖:(數據結構與算法C++.pdf)
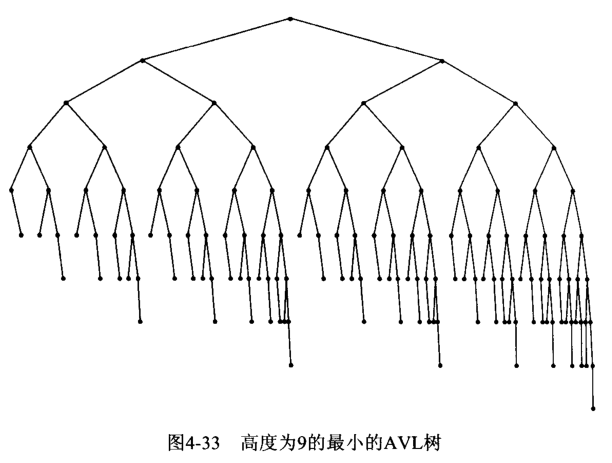
typedef unsigned int typeClass; typedef struct __SET_typeClass_node { typeClass data; struct __SET_typeClass_node *left; struct __SET_typeClass_node *right; u8 heigh; } SET_typeClass_node_t; typedef struct __SET_typeClass_t { SET_typeClass_node_t *root; u32 size; } SET_typeClass_t;
【3 插入】
數據的插入還是依照我們普通的二叉樹進行插入,遞歸判斷我們的數據是否小於當前節點,
小於,遞歸往左走,大於,大於遞歸往右走,等於,不操作,真正的基礎情況是判斷是發現當前
節點為NULL 此時申請內存存儲該元素;

SET_typeClass_node_t *SET_inserttypeClass_node_t(SET_typeClass_node_t *root, u8 (*compare)(const typeClass *a, const typeClass *b), const typeClass *value, u32 *size) { if (root == NULL) { root = (SET_typeClass_node_t *)malloc(sizeof(SET_typeClass_node_t)); if (root == NULL) { // Out of space!!! } else { root->data = (*value); root->left = root->right = NULL; (*size)++; } return root; } else if (compare(value, &root->data)) { root->left = SET_inserttypeClass_node_t(root->left, compare, value, size); } else if (compare(&root->data, value)) { root->right = SET_inserttypeClass_node_t(root->right, compare, value, size); } return root; }
普通二叉樹插入
當我們在做完這一切之後,還需要做的是維護AVL的性質:左右節點高度相差最大為1;且需要
遞歸查詢哦。於是乎我們接下來第一步要做的是什麼呢?
更新我們自己的節點的高度;
root->heigh = SET_Max(SET_heighttypeClass(root->left), SET_heighttypeClass(root->right)) + 1;
更新之後節點之後我們就會發現,哎呀,有些時候(大多數時候)AVL樹的規則被破壞了,那麼該
就需要處理重新符合AVL樹的規則;插入之後呢可能會出現四種情況,其中兩兩鏡像,因此我們只討論
兩種;
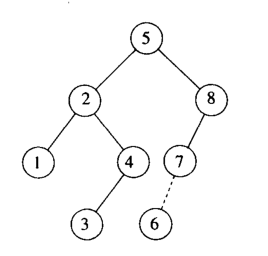
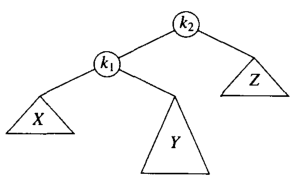
以上兩種情況分別為 LL ,LR,具體判斷標準為:觀察高度開始不符合的節點,8號節點和 K2節點,
這裡說的高度不符的節點表示:左右孩子的高度相差 >1 那麼他們偏離的子節點的方向分別是
8號:Left->Left k2->Left->Right; 我們在處理LL情況的時候,只需要將7號變成5號的右孩子;
8號變成7號的右孩子即可,相當於6~7~8號順時針旋轉了一下,我們把這個定義為 ”左單旋“,旋轉後
變成如下圖:
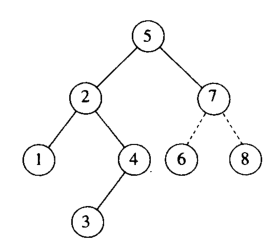
相對應的也有 ”右單旋“咯。大家自己推導啦;
接下來看我們的LR情況,如果僅僅對K2執行一次左單旋,那麼結果是:
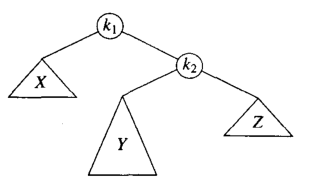
但是這樣依舊沒有滿足 AVL 樹的性質;K2的高度會比 X大超過1;此時我們需要引進一個k1的右節點進行雙旋轉;
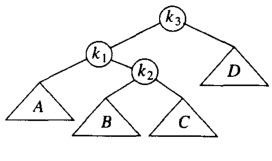
我們首先把 K1 k2 B 進行一次右單旋;得到
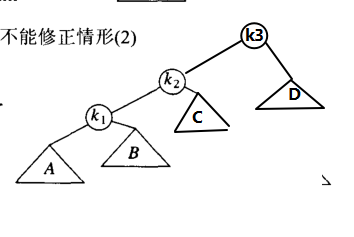
然後我們在將C~k2~k3進行一次左旋:
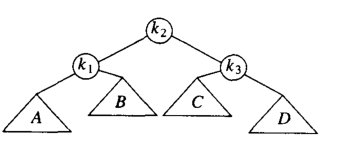
相對應的我們也會有 RL的情況,鏡像情況我們就不贅述咯;
下面代碼是單旋、雙旋的實現:
SET_typeClass_node_t *SET_doubleRotateLefttypeClass(SET_typeClass_node_t *s) { s->left = SET_singleRotateRighttypeClass(s->left); return SET_singleRotateLefttypeClass(s); } SET_typeClass_node_t *SET_doubleRotateRighttypeClass(SET_typeClass_node_t *s) { s->right = SET_singleRotateLefttypeClass(s->right); return SET_singleRotateRighttypeClass(s); } SET_typeClass_node_t *SET_singleRotateLefttypeClass(SET_typeClass_node_t *s) { SET_typeClass_node_t *s1; s1 = s->left; s->left = s1->right; s1->right = s; s->heigh = SET_Max( SET_heighttypeClass(s->left), SET_heighttypeClass(s->right)) + 1; s1->heigh = SET_Max( SET_heighttypeClass(s1->left), s->heigh) + 1; return s1; } SET_typeClass_node_t *SET_singleRotateRighttypeClass(SET_typeClass_node_t *s) { SET_typeClass_node_t *s1; s1 = s->right; s->right = s1->left; s1->left = s; s->heigh = SET_Max( SET_heighttypeClass(s->left), SET_heighttypeClass(s->right)) + 1; s1->heigh = SET_Max( SET_heighttypeClass(s1->right), s->heigh) + 1; return s1; }
綜合以上,我們最後insert的代碼就成了:

SET_typeClass_node_t *SET_inserttypeClass_node_t(SET_typeClass_node_t *root, u8 (*compare)(const typeClass *a, const typeClass *b), const typeClass *value, u32 *size) { if (root == NULL) { root = (SET_typeClass_node_t *)malloc(sizeof(SET_typeClass_node_t)); if (root == NULL) { // Out of space!!! } else { root->data = (*value); root->left = root->right = NULL; root->heigh = 1; (*size)++; } return root; } else if (compare(value, &root->data)) { root->left = SET_inserttypeClass_node_t(root->left, compare, value, size); if (SET_heighttypeClass(root->left) - SET_heighttypeClass(root->right) == 2) { if (compare(value, &root->left->data)) root = SET_singleRotateLefttypeClass(root); else root = SET_doubleRotateLefttypeClass(root); } } else if (compare(&root->data, value)) { root->right = SET_inserttypeClass_node_t(root->right, compare, value, size); if (SET_heighttypeClass(root->right) - SET_heighttypeClass(root->left) == 2) { if (compare(&root->right->data, value)) root = SET_singleRotateRighttypeClass(root); else root = SET_doubleRotateRighttypeClass(root); } } root->heigh = SET_Max(SET_heighttypeClass(root->left), SET_heighttypeClass(root->right)) + 1; return root; }
AVL inser操作
然後我們使用 tree 將其包裝,並且返回是否插入成功;插入不成功有兩種情況(內存空間不足和元素已存在)

u8 SET_inserttypeClass_t(SET_typeClass_t *set, const typeClass ele) { if (set == NULL || set->compare == NULL) return 0; u32 cursize = set->size; set->root = SET_inserttypeClass_node_t(set->root, set->compare, &ele, &set->size); return (cursize < set->size); }
AVL insert 封裝
【4 刪除】
刪除的操作呢,比插入要更加複雜一些;但是我們依舊是從基礎的二叉樹刪除來入手;普通的二叉樹首先
遞歸尋找到數據,然後將數據分成兩種情況:該元素有兩個孩子和該元素沒有兩個孩子;沒有兩個孩子的邏輯就
很簡單,判斷當前左孩子是否為空,是:將元素的指針指向他的右孩子,否則指向左孩子;如果兩個孩子都為NULL,
指向誰都一樣;
如果是有兩個孩子的呢?那麼我們就將這個元素下尋找到他最小的一個子輩(可能是他的孩子、孫子、曾孫、玄孫。。。)
然後把他的子輩賦值給他,然後刪除他的那個子輩;因為他的子輩一定是左孩子為NULL的;
以下為實現:

SET_typeClass_node_t *SET_removetypeClass_node_t(SET_typeClass_node_t *root, u8 (*compare)(const typeClass *a, const typeClass *b), void (*deleteSub)(const typeClass *ele), const typeClass *value, u32 *size) { if (root == NULL) { // no has this value } else if (compare(value, &root->data)) { root->left = SET_removetypeClass_node_t(root->left, compare, deleteSub, value, size); } else if (compare(&root->data, value)) { root->right = SET_removetypeClass_node_t(root->right, compare, deleteSub, value, size); } else { /*real delete option*/ if (root->right != NULL && root->left != NULL) { /* has two child */ SET_typeClass_node_t *temp = root; while (temp->left != NULL) { temp = temp->left; } if (deleteSub != NULL) deleteSub(&root->data); root->data = temp->data; /* deleteSub == NULL because this min not to free ,just become root->data; */ root->left = SET_removetypeClass_node_t(root->left, compare, NULL, &root->data, size); } else { /* has only child or no child */ SET_typeClass_node_t *t = (root->right == NULL) ? (root->left) : (root->right); if (deleteSub != NULL) deleteSub(&root->data); free(root); (*size)--; root = t; } } return root; }
普通二叉樹remove節點
刪除完節點之後,我們依舊需要考慮的問題是平衡的問題;刪除會出現什麼問題呢?我們上述的刪除到最後
一定以刪除一個在末梢的節點(孩子最多只有一個),因此我們只需要考慮此情況即可;
我們可以換一個思路,其實刪除帶來的影響就是在樹的另一邊插入了一個值;那麼相對應的,那邊高度高了我
就往哪邊旋轉就好了;只不過我們判斷的時候如果是刪除左邊,那麼我們就要判斷當前是不是右邊高度-左邊高度 > 2 就好了。
嗯~很簡單是不是?
不不不,在insert中我們判斷是否需要使用雙旋轉的依據是:
因為在插入時,如果出現的不平衡,那麼假設插入的值比當前root的右孩子要大,那麼就會插入在右孩子的左邊;
就會出現下圖所示 (插入了 14 )此時需要雙旋轉,是因為k1的右孩子高度高且右孩子的左側比右側要高;這句話有
點繞口,我們分成兩步,
第一步:k1節點破壞了AVL樹的規則且需要旋轉的是右邊;
第二步:在k1的右孩子k3上,雖然沒有違法AVL的規則,但是他的左孩子高度要比右孩子高度高;這就是我們所說
的RL情況,
所以需要雙旋;
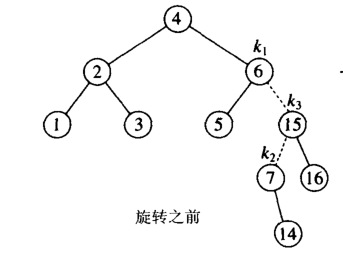
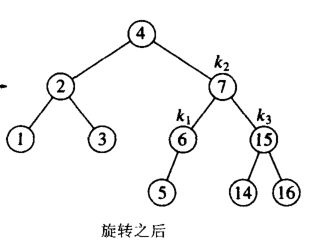
那麼在刪除是,也應遵循此規則,也就是說刪除的時候我們就不要比較 刪除值的大小啦,因為刪除完值之後,
相當於我們需要知道另一側的情況是不是需要雙旋,這個時候怎麼辦呢?我們就依照上述一二步的原理,判斷如果
左邊高度高高於右邊高度 >1 了,那麼我就看左邊孩子的兩個孩子的高度是不是右邊 > 左邊,如果是->雙旋轉,如果
不是,單旋轉;由於有兩個孩子的節點到最後也會是刪除一個葉子節點,故不需要考慮;
以下是remove判斷是否需要雙旋轉的代碼:

if (compare(value, &root->data)) { root->left = SET_removetypeClass_node_t(root->left, compare, deleteSub, value, size); if (SET_heighttypeClass(root->right) - SET_heighttypeClass(root->left) == 2) { if (SET_heighttypeClass(root->right->right) > SET_heighttypeClass(root->right->left)) root = SET_singleRotateRighttypeClass(root); else root = SET_doubleRotateRighttypeClass(root); } }
remove是否需要雙旋轉
需要我們注意的是在刪除有兩個孩子的節點的時候,雖然我們是刪除,但是我實際上還是調用的遞歸,一次我們還
是需要判斷一次平衡規則;
最後remove的代碼如下:

SET_typeClass_node_t *SET_removetypeClass_node_t(SET_typeClass_node_t *root, u8 (*compare)(const typeClass *a, const typeClass *b), void (*deleteSub)(const typeClass *ele), const typeClass *value, u32 *size) { if (root == NULL) { // no has this value } else if (compare(value, &root->data)) { root->left = SET_removetypeClass_node_t(root->left, compare, deleteSub, value, size); if (SET_heighttypeClass(root->right) - SET_heighttypeClass(root->left) == 2) { if (SET_heighttypeClass(root->right->right) > SET_heighttypeClass(root->right->left)) root = SET_singleRotateRighttypeClass(root); else root = SET_doubleRotateRighttypeClass(root); } } else if (compare(&root->data, value)) { root->right = SET_removetypeClass_node_t(root->right, compare, deleteSub, value, size); if (SET_heighttypeClass(root->left) - SET_heighttypeClass(root->right) == 2) { if (SET_heighttypeClass(root->left->left) > SET_heighttypeClass(root->left->right)) root = SET_singleRotateLefttypeClass(root); else root = SET_doubleRotateLefttypeClass(root); } } else { /*real delete option*/ if (root->right != NULL && root->left != NULL) { /* has two child */ SET_typeClass_node_t *temp = root; while (temp->left != NULL) { temp = temp->left; } if (deleteSub != NULL) deleteSub(&root->data); root->data = temp->data; /* deleteSub == NULL because this min not to free ,just become root->data; */ root->left = SET_removetypeClass_node_t(root->left, compare, NULL, &root->data, size); if (SET_heighttypeClass(root->right) - SET_heighttypeClass(root->left) == 2) { if (SET_heighttypeClass(root->right->right) > SET_heighttypeClass(root->right->left)) root = SET_singleRotateRighttypeClass(root); else root = SET_doubleRotateRighttypeClass(root); } } else { /* has only child or no child */ SET_typeClass_node_t *t = (root->right == NULL) ? (root->left) : (root->right); if (deleteSub != NULL) deleteSub(&root->data); free(root); (*size)--; root = t; } } if (root != NULL) root->heigh = SET_Max(SET_heighttypeClass(root->left), SET_heighttypeClass(root->right)) + 1; return root; }
AVL remove 代碼
同理使用一個tree對他進行封裝,同時返回是否remove成功,remove不成功只有一種可能,那就是set中不存在此元素;
u8 SET_removetypeClass_t(SET_typeClass_t *set, const typeClass ele) { if (set == NULL || set->compare == NULL) return 0; u32 cursize = set->size; set->root = SET_removetypeClass_node_t(set->root, set->compare, set->deleteSub, &ele, &set->size); return (cursize > set->size); }
在AVL樹中最重要的就是插入和刪除啦;
其他的像 delete 遍歷呀,find findMax之類的太簡單我就不說啦。基本上就是使用遍歷或者一直往右找或往左找;
最後我考慮到上文中SET_typeClass_t是一個類型,所以所有的比較都抽象化了compare函數,還有有可能在刪除的時候
需要釋放SET_typeClass_t中指向的空間,所以抽象化成為函數指針deleteSub;
【結束語】
下一節就是將我們今天所實現的這些函數變成宏,完成 STL 數據容器 SET
目錄
1.引言
3.2 C語言_實現數據容器set(基礎版)
4 C語言_實現簡單基礎的map
參考資料 : 數據結構與算法C++實現.pdf;


