利用邏輯回歸進行簡單的人群分類解決廣告推薦問題

• 2019 年 10 月 24 日
• 筆記

一、什麼是邏輯回歸？

　　邏輯回歸又稱對數幾率回歸是離散選擇法模型之一，邏輯回歸是一種用於解決監督學習問題的學習算法，進行邏輯回歸的目的是使訓練數據的標籤值與預測出來的值之間的誤差最小化。logistic回歸的因變量可以是二分類的，也可以是多分類的，但是二分類的更為常用，也更加容易解釋，多類可以使用softmax方法進行處理。實際中最為常用的就是二分類的logistic回歸。

Logistic回歸模型的適用條件：

1. 因變量為二分類的分類變量或某事件的發生率，並且是數值型變量。但是需要注意，重複計數現象指標不適用於Logistic回歸。
2. 殘差和因變量都要服從二項分佈。二項分佈對應的是分類變量，所以不是正態分佈，進而不是用最小二乘法，而是最大似然法來解決方程估計和檢驗問題。
3. 自變量和Logistic概率是線性關係
4. 各觀測對象間相互獨立

原理：

　　如果直接將線性回歸的模型扣到Logistic回歸中，會造成方程二邊取值區間不同和普遍的非直線關係。因為Logistic中因變量為二分類變量，某個概率作為方程的因變量估計值取值範圍為0-1，但是，方程右邊取值範圍是無窮大或者無窮小。所以，才引入Logistic回歸。

Logistic回歸實質：

　　發生概率除以沒有發生概率再取對數。就是這個不太繁瑣的變換改變了取值區間的矛盾和因變量自變量間的曲線關係。究其原因，是發生和未發生的概率成為了比值 ，這個比值就是一個緩衝，將取值範圍擴大，再進行對數變換，整個因變量改變。不僅如此，這種變換往往使得因變量和自變量之間呈線性關係，這是根據大量實踐而總結。所以，Logistic回歸從根本上解決因變量要不是連續變量怎麼辦的問題。還有，Logistic應用廣泛的原因是許多現實問題跟它的模型吻合。例如一件事情是否發生跟其他數值型自變量的關係。

二、Logistic函數/sigmoid函數的原理與實現

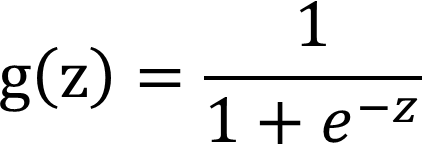
實現：

import numpy as np  import matplotlib.pyplot as plt  x=np.linspace(-6,6,1000)  y=[1/(1+np.exp(-i)) for i in x]  plt.plot(x,y)  plt.grid(True)

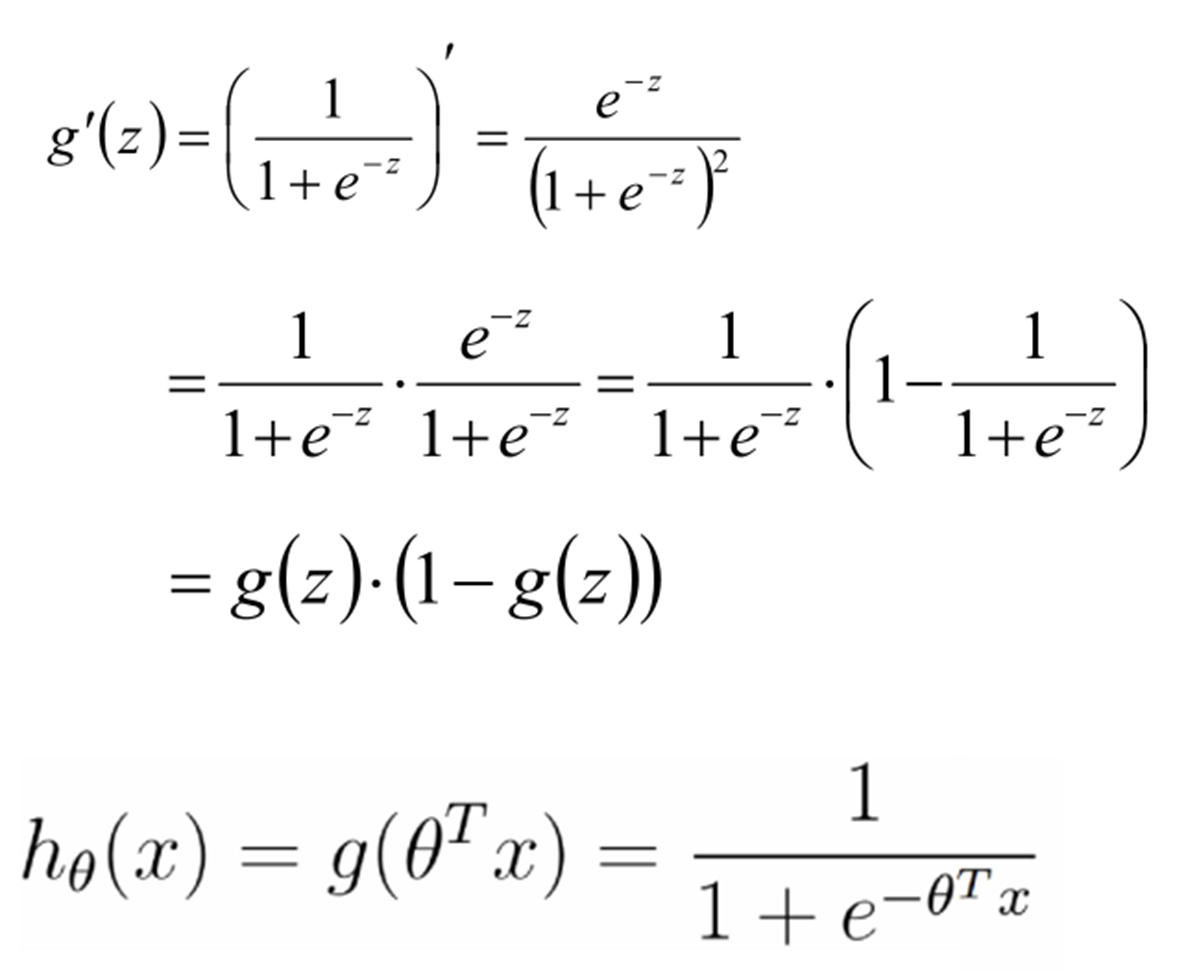
最大似然估計

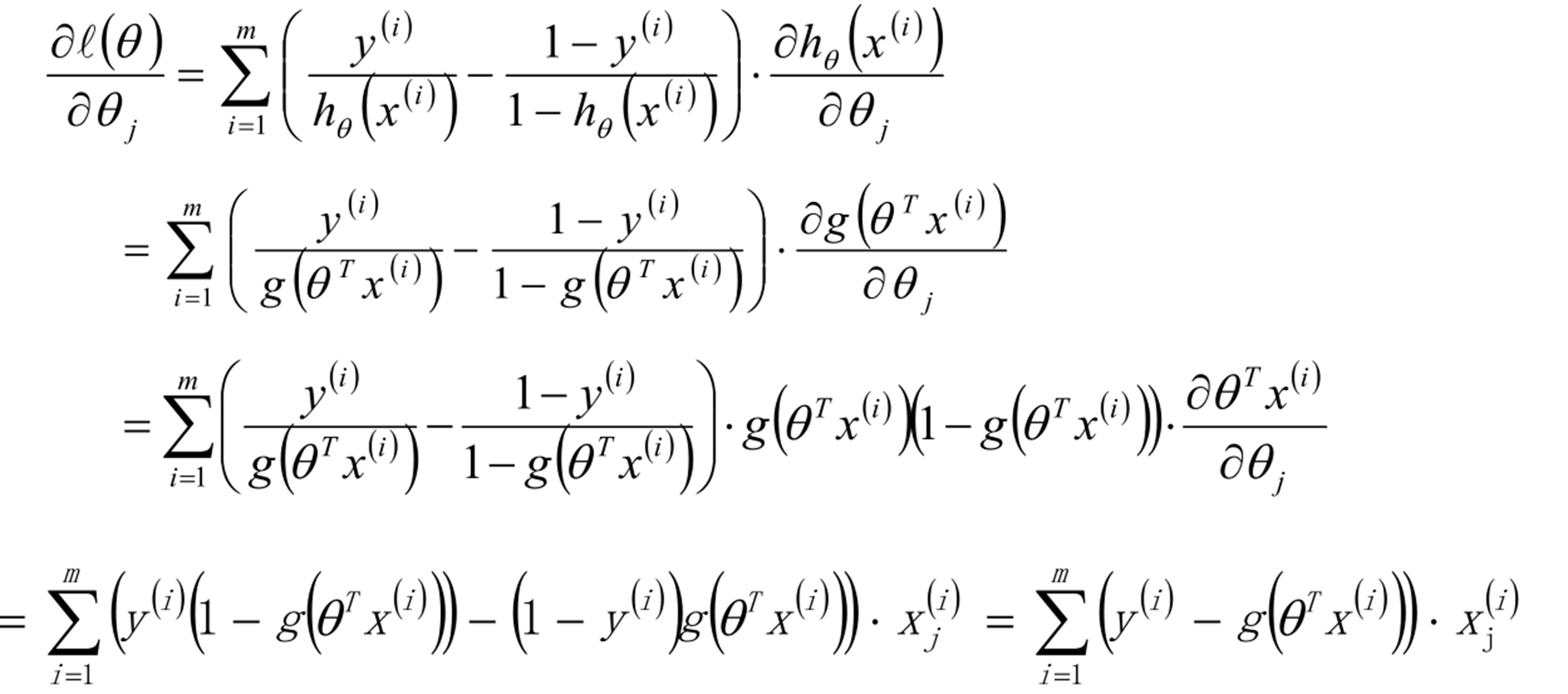
結論：

假設

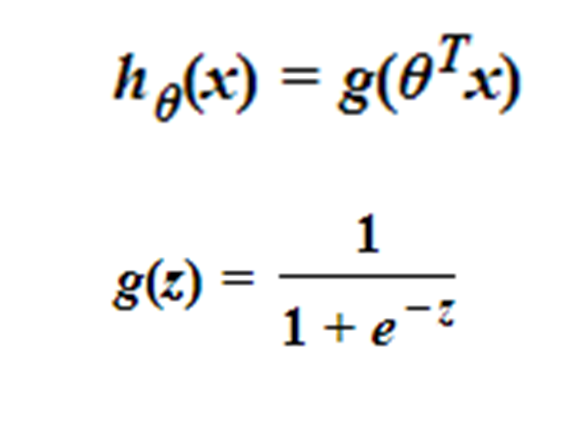
損失函數

梯度

三、為了進行廣告推薦對目標人群簡單分類

1.邏輯回歸步驟

1. 收集數據
2. 讀取數據，處理數據，查看各數據的缺失情況（如果缺失需要藉助於刪除法、替換法、插值法等 完成缺失值的處理）對定性變量數值化，剔除無關變量，構建常數項
3. 分析數據，將數據分為訓練集和測試集，交叉驗證，構建邏輯回歸分類器，調整優化，得出參數值
4. 測試算法，完成預測

2.以一組可能買房的用戶信息數據為例

（User ID：用戶id Gender：性別 Age：年齡 EstimatedSalary：收入 Purchased：是否已經購買）

3.代碼示例：

import pandas as pd  import matplotlib.pyplot as plt  purchase=pd.read_csv("logistic_data.csv")  purchase.head()  dummy = pd.get_dummies(purchase.Gender)  dummy.head()  # 為防止多重共線性，將啞變量中的Female刪除  dummy_drop = dummy.drop('Female', axis = 1)#把female列刪除  dummy_drop.head()  purchase = purchase.drop(['User ID','Gender'], axis = 1)  model_data = pd.concat([dummy_drop,purchase], axis = 1)  X = model_data.drop('Purchased', axis = 1)  y = model_data['Purchased']  X.head()  model_data['Purchased'].value_counts()    from sklearn import linear_model  clf=linear_model.LogisticRegression()  clf.fit(X,y)  clf.coef_  clf.score(X,y)

四、邏輯回歸優缺點

1.優點