python常用算法（5）——樹，二叉樹與AVL樹

2019 年 10 月 21 日
筆記

1，樹

　　樹是一種非常重要的非線性數據結構，直觀的看，它是數據元素（在樹中稱為節點）按分支關係組織起來的結構，很像自然界中樹那樣。樹結構在客觀世界中廣泛存在，如人類社會的族譜和各種社會組織機構都可用樹形象表示。樹在計算機領域中也得到了廣泛應用，如在編譯源程序時，可用樹表示源程序的語法結構。又如在數據庫系統中，樹型結構也是信息的重要組織形式之一。一切具有層次關係的問題都可以用樹來描述。

　　樹（Tree）是元素的集合。樹的定義是遞歸的，樹是一種遞歸的數據結構。比如：目錄結構。樹是由n個結點組成的集合：如果n=0，那這就是一顆空樹；如果 n>0，那麼存在1個結點作為樹的根節點，其他結點可以分為m個集合，每個集合本身又是一棵樹。

1，樹的根結點沒有前驅結點，除根結點之外所有結點有且只有一個前驅結點。
2，樹中所有結點可以有零個或者多個後繼結點。

1.1 樹的術語

根節點：樹的第一個節點，沒有父節點的節點
葉子節點：不帶分叉的節點
樹的深度（高度）：就是分了多少層
孩子節點，父節點：節點與節點之間的關係

　　如下圖，我們分別解釋：

　 1）B是K的祖先結點，K是B的子孫節點，E是K的雙親節點，K是E的孩子節點，K是L的兄弟節點。

　　2）樹中一個結點的子節點個數為該節點的度，樹中結點最大度數為樹的度。

　　3）度大於0為節點結點，度等於0為葉子結點。

　　4）結點層次如圖，結點深度時從根結點從頂往下累加，結點高度從低往上累加，樹的高度（深度）是樹的最大層數。

　　5）有序樹：從左到右有次序，有關聯。反之為無序樹。

　　6）兩結點之間的路徑是兩個結點之間所經過的結點序列構成的，路徑長度是路徑上所經過的邊的個數。

　　7）森林是 m （m >=0）棵互不相交的集合。

　　上面觀察實際上給了我們一種嚴格的定義樹的方法：

1，樹是元素的集合
2，該集合可以為空，這時樹中沒有元素，我們稱樹為空樹（empty tree）
3，如果該集合不為空，那麼該集合有一個根節點，以及0個或者多個子樹。根節點與他的子樹的根節點用一個邊（edge）相連。

1.2 樹的實現

　　樹的示意圖已經給出了樹的一種內存實現方法：每個節點存儲元素和多個指向子節點的指針。然而，子節點數目的是不確定的。一個父節點可能有大量的子節點，而另一個父節點可能只有一個子節點，而樹的增刪節點操作會讓子節點的數目發生進一步的變換。這種不確定性就可能就可能帶來大量的內存相關操作，並且容易造成內存的浪費。

　　一種經典的實現方法如下：

　　樹的內存實現：擁有同一父節點的兩個結點互為兄弟節點（sibling）。上圖的實現方式中，每個節點包含一個指針指向第一個子節點，並且有另一個指針指向他的下一個兄弟節點。這樣，我們就可以用統一的，確定的結構來表示每個節點。

1.3 樹的實例——模擬文件系統

　　代碼如下：

#_*_coding:utf-8_*_    class Node:      def __init__(self, name, type='dir'):          self.name = name          self.type = type  # 'dir'  or ; 'file'          self.children = []          self.parent = None          # 鏈式存儲        def __repr__(self):          return self.name      class FileSystemTree:      def __init__(self):          self.root = Node("/")  # 首先我們創建一個根目錄          self.now = self.root        def mkdir(self, name):          # 創建一個文件目錄，所以我們必須保證name是以 /結尾，如果沒有，我們就加          if name[-1] != '/':              name += '/'          node = Node(name)          # 創建一個文件目錄          self.now.children.append(node)          node.parent = self.now        def ls(self):          # 展示當前文件夾下的文件          return self.now.children        def cd(self, name):          # 切換到指定目錄  注意：支持絕對路徑和相對路徑          # 相對路徑是從now的路徑下開始，而絕對路徑是從root路徑下開始找          if name[-1] != '/':              name += '/'          if name == '../':              self.now = self.now.parent              return          for child in self.now.children:              if child.name == name:                  # 如果傳入的目錄名等於孩子的目錄名，我們直接切換                  self.now = child                  return          raise ValueError("invalid dir")      tree = FileSystemTree()  tree.mkdir('var/')  tree.mkdir('bin/')  tree.mkdir('usr/')  print(tree.ls())  # [var/, bin/, usr/]  tree.cd('bin/')  print(tree.ls())  # []  print(tree.root.children)  # [var/, bin/, usr/]

2，二叉樹

2.1 二叉樹的定義

　　二叉樹的鏈式存儲：將二叉樹的節點定義為一個對象，節點之間通過類似鏈表的鏈接方式來連接。

　　二叉樹是一種特殊的樹，它具有以下特點：

　　1）至多只有兩棵子樹，二叉樹有左右之分，次序不能顛倒，也是遞歸形式定義。

　　2）或者為空二叉樹，即 n=0

　　3）或者由一個根結點和兩個互不相交的被稱為根的左子樹和右子樹組成。左子樹和右子樹又分別是一顆二叉樹。

　　4）每個節點至多有兩個節點，即每個節點的度最多為2

　　5）二叉樹中所有節點的形態有5種：空節點，無左右子樹的節點，只有左子樹的節點，只有右子樹的節點和具有左右子樹的節點

　　二叉樹的定義如下：

class BiTreeNode:      def __init__(self, data):          self.data = data          self.lchild = None  # 左孩子          self.rchild = None  # 右孩子    a = BiTreeNode("A")  b = BiTreeNode("B")  c = BiTreeNode("C")  d = BiTreeNode("D")  e = BiTreeNode("E")  f = BiTreeNode("F")  g = BiTreeNode("G")    e.lchild = a  e.rchild = g  a.rchild = c  c.lchild = b  c.rchild = d  g.rchild = f    root = e  print(root.lchild.rchild.data)

　　二叉樹的節點定義：

class BiTreeNode:      def __init__(self, data):          self.data = data          self.lchild = None  # 左孩子          self.rchild = None  # 右孩子

2.2 二叉樹與度為2的有序樹的區別：

　　1）度為2的樹至少有3個結點，而二叉樹可以為空。

　　2）左右次數。

2.3 二叉樹的存儲方式

　　二叉樹的存儲結構分為鏈式存儲結構和順序存儲結構（列表）

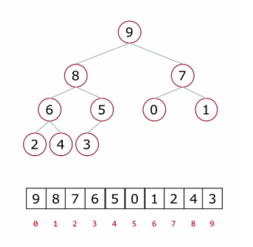
二叉樹的順序存儲方式

　　思考：父節點和左孩子節點的編號下標有什麼關係？

　　 0-1 1-3 2-5 3-7 4-9 i —-> 2i+1

　　父節點和右孩子節點的編號下標有有什麼關係？

　　0-2 1-4 2-6 3-8 4-10 i —–> 2i+2

二叉樹的鏈式存儲

　　結構採用鏈式存儲二叉樹中的數據元素，用鏈建立二叉樹中結點之間的關係。二叉樹最常用的鏈式存儲結構是二叉鏈，每個節點包含三個域，分別是數據元素域 data，左孩子鏈域 LChild 和右孩子鏈域 rChild。與單鏈錶帶頭結點和不帶頭節點的兩種情況相似，二叉鏈存儲結構的二叉樹也有帶頭結點和不帶頭節點兩種。

2.4 二叉樹的遍歷

　　那麼如何遍歷一顆二叉樹呢？其實有兩種通用的遍歷樹策略：

深度優先搜索（DFS）

　　在這個策略中，我們採用深度作為優先級，以便從根開始一直到達某個確定的葉子，然後再返回根到達另一個分支。

　　深度優先搜索策略又可以根據根節點，左孩子和右孩子的相對順序被細分為先序遍歷，中序遍歷和後序遍歷。

寬度優先搜索（BFS）

　　我們按照高度順序一層一層的訪問整棵樹，高層次的節點將會被低層次的節點先被訪問到。

下圖中的頂點按照訪問的順序編號，按照1-2-3-4-5 的順序來比較不同的策略：

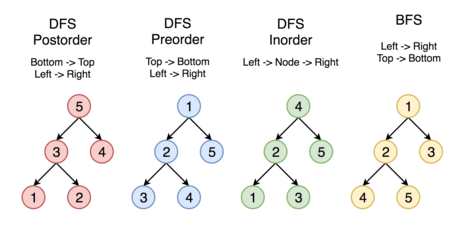
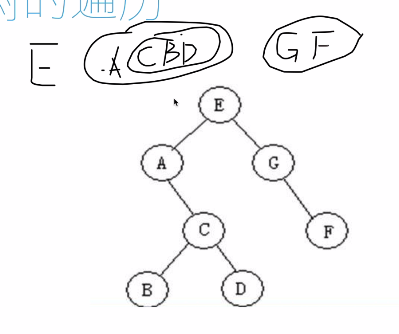
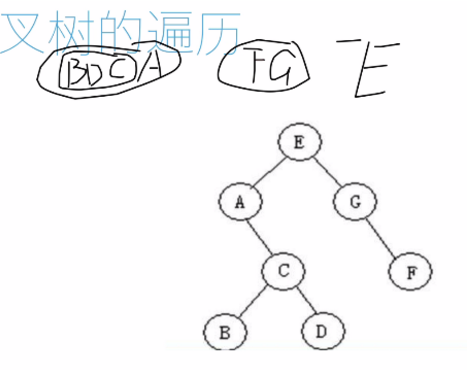
　　下面學習二叉樹的遍歷方式，以下圖的二叉樹為例，我們分別學習前序遍歷，中序遍歷，後序遍歷，層次遍歷。

前序遍歷

　　思想：先訪問根節點，再先序遍歷左子樹，然後再序遍歷右子樹。總的來說是根——左——右

　　前序遍歷如圖所示：

　　代碼如下：

# 二叉樹的前序遍歷  def pre_order(root):      if root:          print(root.data)  # 先打印根節點          pre_order(root.lchild)          pre_order(root.rchild)    # pre_order(root)  '''  E  A  C  B  D  G  F  '''

中序遍歷

　　思想：先中序訪問左子樹，再序訪問根節點，最後中序遍歷右子樹。總的來說是左——根——右

　　中序遍歷如圖所示：

　　代碼如圖所示：

# 中序遍歷  def in_order(root):      if root:          in_order(root.lchild)          print(root.data)          in_order(root.rchild)    # in_order(root)  '''  A  B  C  D  E  G  F  '''

後序遍歷

　　思想：先後續訪問左子樹，然後後續訪問右子樹，最後訪問根，總的來說是左——右——根

　　後序遍歷如圖所示：

　　代碼如下：

# 後序遍歷  def post_order(root):      if root:          post_order(root.lchild)          post_order(root.rchild)          print(root.data)    post_order(root)  '''  B  D  C  A  F  G  E  '''

層次遍歷（寬度優先遍歷）

　　思想：利用隊列，依次將根，左子樹，右子樹存入隊列，按照隊列的先進先出規則來實現層次遍歷。

　　代碼如下：

from collections import deque    def level_order(root):      queue = deque()      queue.append(root)      while len(queue) > 0:  # 只要隊不空          node = queue.popleft()          print(node.data)          if node.lchild:              queue.append(node.lchild)          if node.rchild:              queue.append(node.rchild)    level_order(root)  '''  E  A  G  C  F  B  D  '''

3 幾個特殊的二叉樹

3.1 滿二叉樹

　　滿二叉樹作為一種特殊的二叉樹，它是指：除了葉子節點，所有節點都有兩個孩子（左子樹和右子樹），並且所有葉子節點深度都一樣。

　　其特點有：

1）葉子節點只能出現在最下面一層
2）非葉子節點度一定是2
3）在同樣深度的二叉樹中，滿二叉樹的節點個數最多，節點個數為：2^h-1，其h為樹的深度。

3.2 完全二叉樹

　　完全二叉樹是由滿二叉樹引申而來，假設二叉樹深度為 h，那麼除了第h層外，之前的每一層（1~h-1）的節點數都達到最大，即沒有空的位置，而且第K層的子節點也都集中在左子樹上（順序）。

　　其具有以下特點：

1）葉子節點可以出現在最後一層或倒數第二層
2）最後一層的葉子節點一定集中在左部連續位置
3）完全二叉樹嚴格按層序編號（可利用數組或列表實現，滿二叉樹同理）
4）若一個節點為葉子節點，那麼編號比其大的節點均為葉子節點

3.3 二叉排序樹

　　一顆二叉樹或者空二叉樹，如：左子樹上所有關鍵字均小於根結點的關鍵字，右子樹上的所有結點的關鍵字均大於根結點的關鍵字，左子樹和右子樹各是一顆二叉排序樹。

3.4 平衡二叉樹

　　樹上任何一結點的左子樹和右子樹的深度只差不超過1 。

4，二叉搜索樹（BST）

4.1 二叉搜索樹的定義

　　二叉搜索樹(Binary Search Tree)，又名二叉排序樹(Binary Sort Tree)。

　　由於二叉樹的子節點數目確定，所以可以直接採用下圖方式在內存中實現。每個節點有一個左子節點（left children）和右子節點（right children）。左子節點是左子樹的根節點，右子節點是右子樹的根節點。

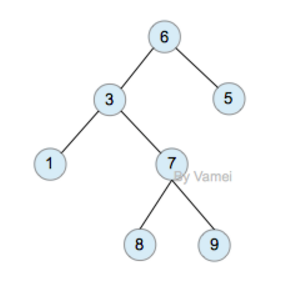
　　如果我們給二叉樹加一個額外的條件，就可以得到一種被稱為二叉搜索樹（binary search tree）的特殊二叉樹。二叉搜索樹要求：每個節點都不比它左子樹的任意元素小，而且不比它的右子樹的任意元素大。

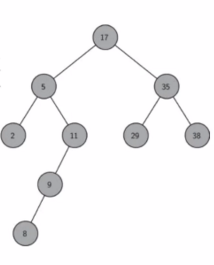
　　二叉搜索樹是一顆二叉樹且滿足性質：設x是二叉樹的一個節點。如果 y 是 x 左子樹的一個節點，那麼 y.key <= x.key；如果y 是x 的右子樹的一個節點，那麼 y.key >= x.key。

4.2 二叉搜索樹的性質

1）若左子樹不為空，則左子樹上所有節點的值均小於或等於它的根節點的值
2）若右子樹不為空，則右子樹上所有節點的值均大於或等於它的跟節點的值
3）左右子樹也分別為二叉搜索樹

　　二叉搜索樹，注意樹中元素的大小。二叉搜索樹可以方便的實現搜索算法。在搜索元素 x 的時候，我們可以將 x 和根節點比較：

1，如果 x 等於根節點，那麼找到 x ,停止搜索（終止條件）
2，如果 x 小於根節點，那麼搜索左子樹
3，如果 x 大於根節點，那麼搜索右子樹

　　二叉搜索樹所需要進行的操作次數最多與樹的深度相等。n個結點的二叉搜索樹的深度最多為 n ，最少為 log(n).

4.3 二叉搜索樹的插入操作

　　從根節點開始，若插入的值比根節點的值小，則將其插入根節點的左子樹；若比根節點的值大，則將其插入根節點的右子樹。該操作可以使用遞歸進行實現。

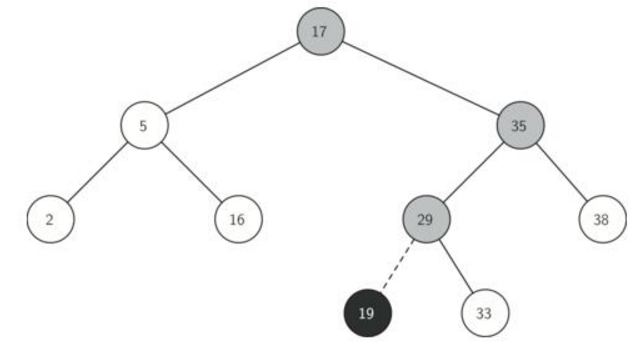
　　代碼如下：

class BiTreeNode:      def __init__(self, data):          self.data = data          self.lchild = None  # 左孩子          self.rchild = None  # 右孩子          self.parent = None      class BST:      def __init__(self, li=None):          self.root = None          if li:              for val in li:                  self.insert_no_rec(val)        def insert(self, node, val):          if not node:              node = BiTreeNode(val)          elif val < node.data:              node.lchild = self.insert(node.lchild, val)              node.lchild.parent = node          elif val > node.data:              node.rchild = self.insert(node.rchild, val)              node.rchild.parent = node          return node        def insert_no_rec(self, val):          p = self.root          if not p:  # 空樹              self.root = BiTreeNode(val)              return          while True:              if val < p.data:                  if p.lchild:                      p = p.lchild                  else:  # 左孩子不存在                      p.lchild = BiTreeNode(val)                      p.lchild.parent = p                      return              elif val > p.data:                  if p.rchild:                      p = p.rchild                  else:                      p.rchild = BiTreeNode(val)                      p.rchild.parent = p                      return              else:                  return

4.4 二叉搜索樹的查詢操作

　　從根節點開始查找，待查找的值是否與根節點的值相同，若相同則返回True；否則，判斷待尋找的值是否比根節點的值小，若是則進入根節點左子樹進行查找，否則進入右子樹進行查找。該操作使用遞歸實現。

　　代碼如下：

def query(self, node, val):      if not node:          return None      if node.data < val:          return self.query(node.rchild, val)      elif node.data > val:          return self.query(node.lchild, val)      else:          return node

4.5 二叉樹的查詢操作——找最大值（最小值）

　　查找最小值：從根節點開始，沿着左子樹一直往下，直到找到最後一個左子樹節點，按照定義可知，該節點一定是該二叉搜索樹中的最小值節點。

　　程序代碼如下：

def findMin(self, root):      '''查找二叉搜索樹中最小值點'''      if root.left:          return self.findMin(root.left)      else:          return root

　　查找最大值：從根節點開始，沿着右子樹一直往下，知道找到最後一個右子樹節點，按照定義可知，該節點一定是該二叉搜索樹中的最大值節點。

　　程序代碼如下：

def findMax(self, root):      '''查找二叉搜索樹中最大值點'''      if root.right:          return self.findMax(root.right)      else:          return root

4.6 二叉搜索樹的刪除操作

　　對二叉搜索樹節點的刪除操作分為以下三種情況

　　1，如果要刪除的節點是葉子節點：直接刪除

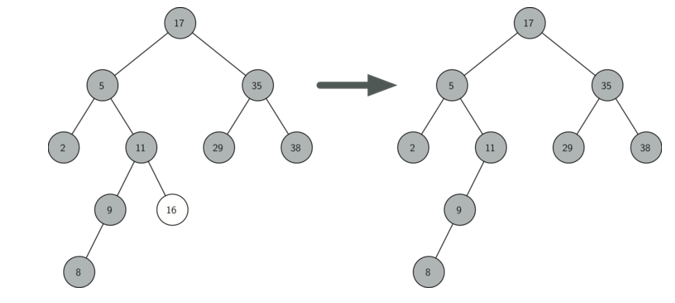
　　2，如果要刪除的節點只有一個孩子：將此節點的父親與孩子連接，然後刪除該節點（注意：該待刪節點可能只有左子樹或者右子樹）

　　3，如果要刪除的節點有兩個孩子：將其右子樹的最小節點（該節點最多有一個右孩子）刪除，並替換當前節點

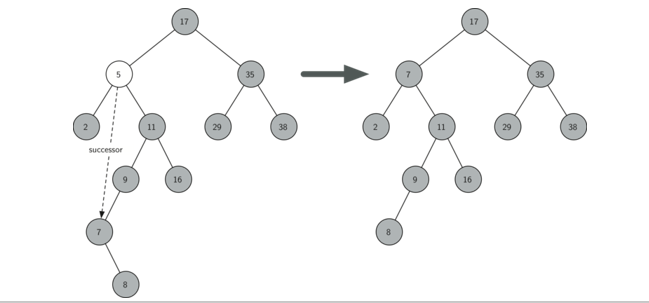
　　代碼如下：

# _*_coding:utf-8_*_  import random      class BiTreeNode:      def __init__(self, data):          self.data = data          self.lchild = None  # 左孩子          self.rchild = None  # 右孩子          self.parent = None      class BST:      def __init__(self, li=None):          self.root = None          if li:              for val in li:                  self.insert_no_rec(val)          def __remove_node_1(self, node):          # 第一種情況：node是葉子節點          if not node.parent:              self.root = None          if node == node.parent.lchild:  # node是他父親的左孩子              node.parent.lchild = None              node.parent = None  # 可以不寫          else:  # node是他父親的右孩子              node.parent.rchild = None        def __remove_node_21(self, node):          # 情況2.1:node只有一個孩子，且為左孩子          if not node.parent:  # 根節點              self.root = node.lchild              node.lchild.parent = None          elif node == node.parent.lchild:  # node是它父親的左孩子              node.parent.lchild = node.lchild              node.lchild.parent = node.parent          else:  # node 是它父親的右孩子              node.parent.rchild = node.lchild              node.lchild.parent = node.parent        def __remove_node_22(self, node):          # 情況2.2：node只有一個孩子，且為右孩子          if not node.parent:              self.root = node.rchild          elif node == node.parent.lchild:              node.parent.lchild = node.rchild              node.rchild.parent = node.parent          else:              node.parent.rchild = node.rchild              node.rchild.parent = node.parent        def delete(self, val):          if self.root:  # 不是空樹              node = self.query_no_rec(val)              if not node:  # 不存在                  return False              if not node.lchild and not node.rchild:  # 1，葉子節點                  self.__remove_node_1(node)              elif not node.rchild:  # 2.1 只有一個左孩子                  self.__remove_node_21(node)              elif not node.lchild:  # 2.2 只有一個右孩子                  self.__remove_node_22(node)              else:                  # 3,兩個孩紙都有                  min_node = node.rchild                  while min_node.lchild:  # 有左孩子                      min_node = min_node.lchild                  node.data = min_node.data                  # 刪除min_node                  if min_node.rchild:                      self.__remove_node_22(min_node)                  else:                      self.__remove_node_1(min_node)

4.7 二叉搜索樹的打印操作

　　實現二叉搜索樹的前序遍歷，中序遍歷，後序遍歷，並打印出來。其中中序遍歷打印出來的數列是按照遞增順序排列。

　　程序的代碼如下：

def printTree(self, root):      # 打印二叉搜索樹（中序打印，有序數列—）      if root == None:          return      self.printTree(root.left)      print(root.val, end=',')      self.printTree(root.right)

4.8 二叉樹的插入，查詢，刪除，打印完整代碼

　　代碼如下：

# _*_coding:utf-8_*_  import random      class BiTreeNode:      def __init__(self, data):          self.data = data          self.lchild = None  # 左孩子          self.rchild = None  # 右孩子          self.parent = None      class BST:      def __init__(self, li=None):          self.root = None          if li:              for val in li:                  self.insert_no_rec(val)        def insert(self, node, val):          if not node:              node = BiTreeNode(val)          elif val < node.data:              node.lchild = self.insert(node.lchild, val)              node.lchild.parent = node          elif val > node.data:              node.rchild = self.insert(node.rchild, val)              node.rchild.parent = node          return node        def insert_no_rec(self, val):          p = self.root          if not p:  # 空樹              self.root = BiTreeNode(val)              return          while True:              if val < p.data:                  if p.lchild:                      p = p.lchild                  else:  # 左孩子不存在                      p.lchild = BiTreeNode(val)                      p.lchild.parent = p                      return              elif val > p.data:                  if p.rchild:                      p = p.rchild                  else:                      p.rchild = BiTreeNode(val)                      p.rchild.parent = p                      return              else:                  return        def query(self, node, val):          if not node:              return None          if node.data < val:              return self.query(node.rchild, val)          elif node.data > val:              return self.query(node.lchild, val)          else:              return node        def query_no_rec(self, val):          p = self.root          while p:              if p.data < val:                  p = p.rchild              elif p.data > val:                  p = p.lchild              else:                  return p          return None        def pre_order(self, root):          if root:              print(root.data, end=',')              self.pre_order(root.lchild)              self.pre_order(root.rchild)        def in_order(self, root):          if root:              self.in_order(root.lchild)              print(root.data, end=',')              self.in_order(root.rchild)        def post_order(self, root):          if root:              self.post_order(root.lchild)              self.post_order(root.rchild)              print(root.data, end=',')        def __remove_node_1(self, node):          # 第一種情況：node是葉子節點          if not node.parent:              self.root = None          if node == node.parent.lchild:  # node是他父親的左孩子              node.parent.lchild = None              node.parent = None  # 可以不寫          else:  # node是他父親的右孩子              node.parent.rchild = None        def __remove_node_21(self, node):          # 情況2.1:node只有一個孩子，且為左孩子          if not node.parent:  # 根節點              self.root = node.lchild              node.lchild.parent = None          elif node == node.parent.lchild:  # node是它父親的左孩子              node.parent.lchild = node.lchild              node.lchild.parent = node.parent          else:  # node 是它父親的右孩子              node.parent.rchild = node.lchild              node.lchild.parent = node.parent        def __remove_node_22(self, node):          # 情況2.2：node只有一個孩子，且為右孩子          if not node.parent:              self.root = node.rchild          elif node == node.parent.lchild:              node.parent.lchild = node.rchild              node.rchild.parent = node.parent          else:              node.parent.rchild = node.rchild              node.rchild.parent = node.parent        def delete(self, val):          if self.root:  # 不是空樹              node = self.query_no_rec(val)              if not node:  # 不存在                  return False              if not node.lchild and not node.rchild:  # 1，葉子節點                  self.__remove_node_1(node)              elif not node.rchild:  # 2.1 只有一個左孩子                  self.__remove_node_21(node)              elif not node.lchild:  # 2.2 只有一個右孩子                  self.__remove_node_22(node)              else:                  # 3,兩個孩紙都有                  min_node = node.rchild                  while min_node.lchild:  # 有左孩子                      min_node = min_node.lchild                  node.data = min_node.data                  # 刪除min_node                  if min_node.rchild:                      self.__remove_node_22(min_node)                  else:                      self.__remove_node_1(min_node)          def printTree(self, root):          # 打印二叉搜索樹（中序打印，有序數列—）          if root == None:              return          self.printTree(root.left)          print(root.val, end=',')          self.printTree(root.right)    # 刪除  tree = BST([1, 4, 2, 5, 3, 8, 6, 9, 7])  tree.in_order(tree.root)  print(" ")  tree.delete(4)  tree.delete(1)  tree.delete(8)  tree.in_order(tree.root)    '''  # 插入操作  tree = BST([4,6,7,9,2,1,3,5,8])  tree.pre_order(tree.root)  print(" ")  tree.in_order(tree.root)  print(" ")  tree.post_order(tree.root)  print(" ")  '''  4, 2, 1, 3, 6, 5, 7, 9, 8,  1, 2, 3, 4, 5, 6, 7, 8, 9,  1, 3, 2, 5, 8, 9, 7, 6, 4,  '''    # 查詢操作  li = list(range(0, 500, 2))  random.shuffle(li)    tree = BST(li)  print(tree.query_no_rec(4).data)  # 4    '''

4.9 二叉搜索樹的效率

　　平均情況下，二叉搜索樹進行搜索的時間複雜度為O(nlgn)

　　最壞情況下，二叉搜索樹可能非常偏斜，如下圖所示：

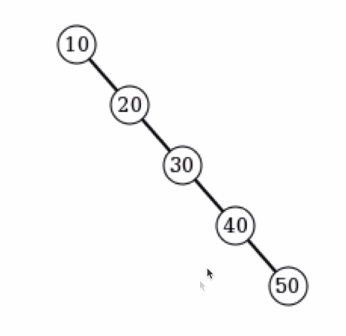
解決方案：

隨機化傳入
AVL樹

5，AVL樹

5.1 AVL樹的定義

　　在計算機科學中，AVL樹（發明此樹的三位科學家的名字首字母）是最早被發明的自平衡二叉查找樹。在AVL樹中，任一節點對應的兩棵子樹的最大高度為1，因此他也被稱為高度平衡樹。查找，插入和刪除在平均和最壞的情況下的時間複雜度都是 O(log n)。增加和刪除元素的操作則可能需要藉由一次或多次樹旋轉，以實現樹的重新平衡。

　　節點的平衡因子是它的左子樹的高度減去它的右子樹的高度（有時相反）。帶有平衡因子1， 0或者-1的節點被認為是平衡的。帶有平衡因子 -2 或 2的節點被認為是不平衡的，並需要重新平衡這個樹，平衡因子可以直接存儲在每個節點中，或從可能存儲在節點的子樹高度計算出來。

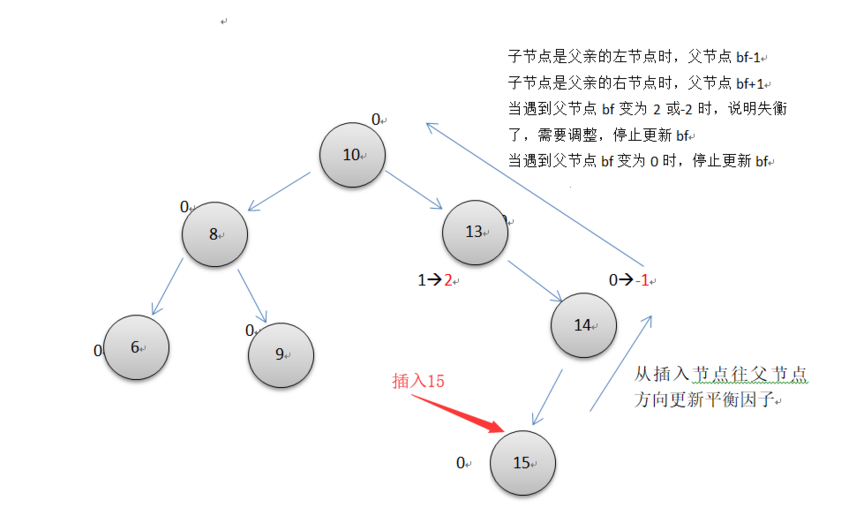
　　AVL樹是一顆自平衡的二叉搜索樹。一般要求每個節點的左子樹和右子樹的高度最多差1（空樹的高度定義為 -1）。在高度為 h 的AVL樹中，最少的節點數 S(h) = S(h-1) + S(h-2) + 1 得到，其中 S(0) = 1， S(1) = 2。

　　如下圖所示，分別為高度為0， 1， 2， 3的AVL樹所需要的最少節點數：

5.2 AVL樹的性質

AVL樹本質上還是一顆二叉搜索樹
根的左右子樹的高度之差的絕對值（平衡因子）不能超過1
根的左右子樹都是平衡二叉樹（二叉排序樹，二叉搜索樹）

5.3 AVL樹的複雜度

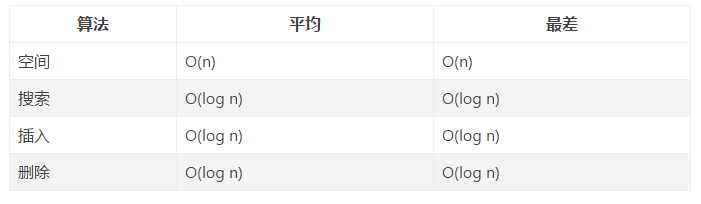
5.3 旋轉

　　旋轉是AVL樹最重要的操作了，理解了旋轉就理解了AVL樹的實現原理。

左單旋轉

　　下圖節點上面的數字表示平衡因子

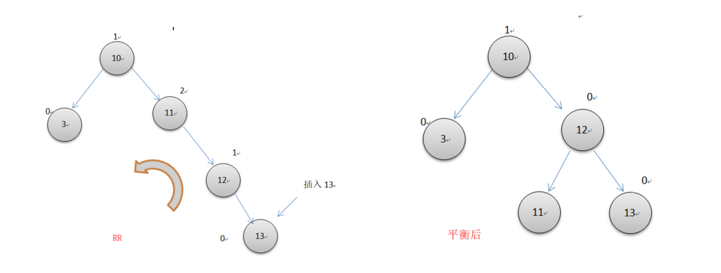
　　如上圖所示，插入13後，右邊子樹11節點的平衡因子變為了2（左右節點的高度差），整個AVL樹開始不平衡，這時便要開始以12為軸心進行一次左單旋轉。具體旋轉操作時原來11的父節點10指向12,12的左節點指向11，而11的右節點指向原來的12的左節點（此例中，12的左節點為空）。

右單旋轉

　　上圖中插入3後左子樹不平衡了，根節點8的平衡因子變為了-2，此時應該以6為軸心向右單旋轉一次，具體操作與左單旋轉類似：8的左節點指向6的有節點（此時為7），6的右節點指向8，由於8原來是跟節點，沒有父節點，所以根節點指向6.旋轉後6和8節點都恢復0的平衡因子了。

左右雙旋轉

　　如上圖所示，10節點的平衡因子是 -2，而它的左節點的平衡因子卻為1，兩個節點失去平衡的方向不一樣，所以要先以7位軸心對節點6左單旋轉一次，再以7為軸心對節點10右旋轉一次。操作細節與上面單次循環一樣。注意此時操作的3個結點的平衡因子要根據不同7的平衡因子單獨調整。

右左雙旋轉

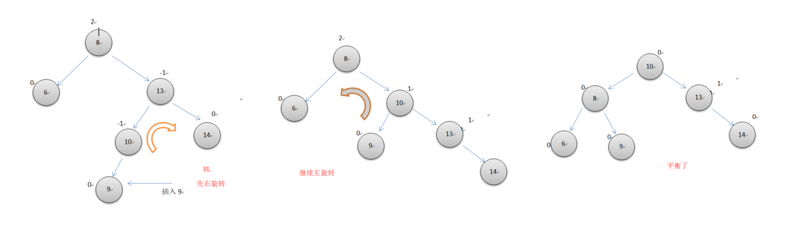
　　如上圖所示，當一個節點的平衡因子為2，而它的右子節點的平衡因子為-1時，就需要先進行右旋轉，再左旋轉。注意中間節點13右旋轉後的平衡因子變為1了。代碼同左右雙旋轉類似。

5.4 AVL樹——插入

　　插入一個節點可能會破壞 AVL樹的平衡，可以通過旋轉操作來進行修正。

　　插入一個節點後，只有從插入節點到根節點的路徑上的節點的平衡可能被改變。我們需要找出第一個破壞了平衡條件的節點，稱之為K，K的兩棵子樹的高度差2.

　　不平衡的出現可能有四種情況：

1，對K的左兒子的左子樹進行一次插入

2，對K的左兒子的左子樹進行一次插入

3，對K的右兒子的左子樹進行一次插入

4，對K的右兒子的右子樹進行一次插入

　　情況1和4是對稱的，需要進行一次單旋轉操作，情況2與3需要一次雙旋轉操作。

AVL插入——左旋

　　不平衡是由於對K的右孩子的右子樹插入導致的：左旋

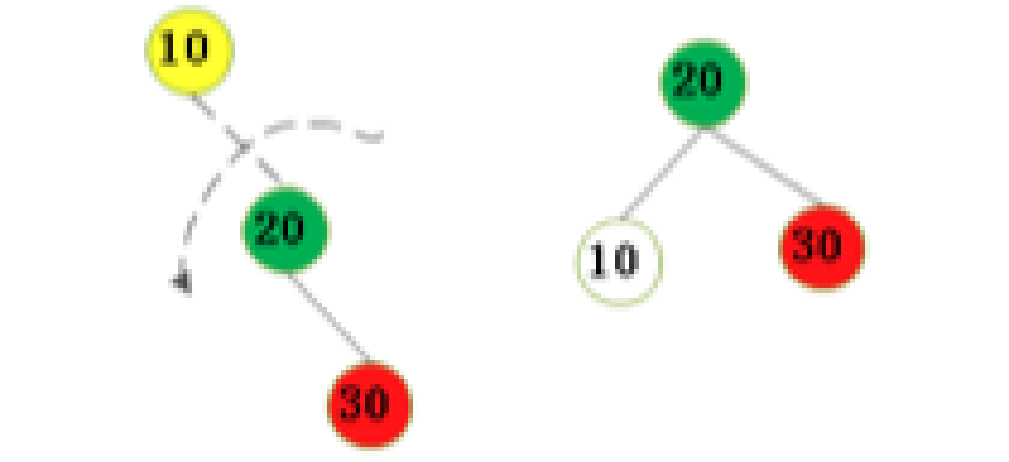
　　那代碼過程如下圖所示：

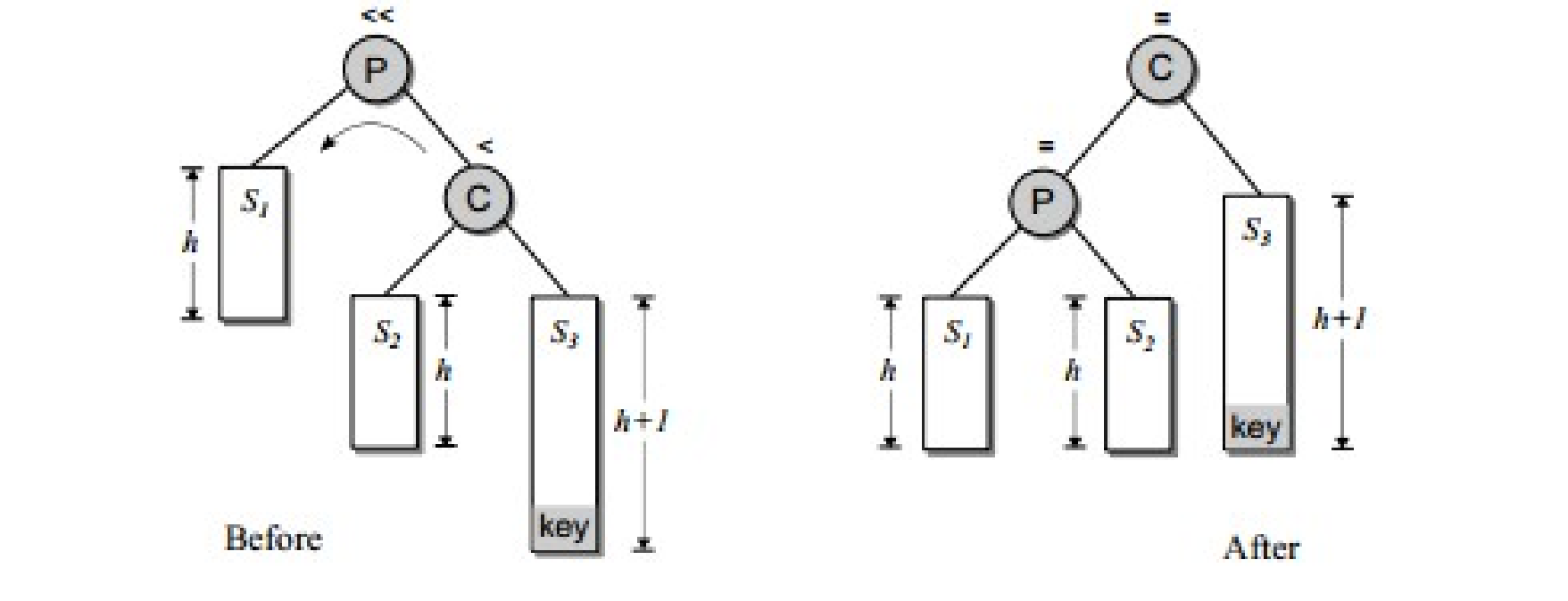
　　代碼如下：

#_*_coding:utf-8_*_  from bst import BiTreeNode, BST      class AVLNode(BiTreeNode):      def __init__(self, data):          BiTreeNode.__init__(self, data)          self.bf = 0    class AVLTree(BST):      def __init__(self, li=None):          BST.__init__(self, li)        def rotate_left(self, p, c):          s2 = c.lchild          p.rchild = s2          if s2:              s2.parent = p          c.lchild = p          p.parent = c            p.bf = 0          c.bf = 0

AVL插入——右旋

　　不平衡是由於對K的左孩子的左子樹插入導致的：右旋

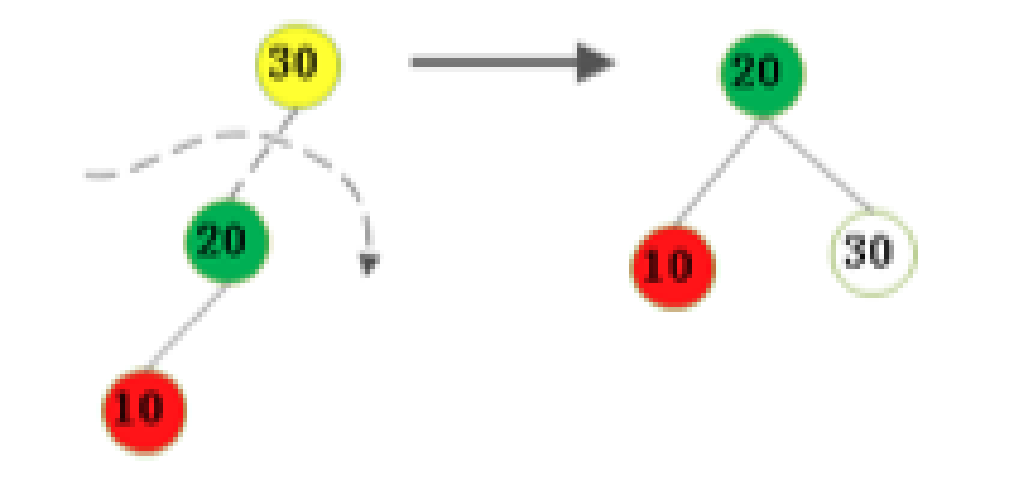
　　右旋插入的過程如下圖：

　　代碼如下：

#_*_coding:utf-8_*_  from bst import BiTreeNode, BST      class AVLNode(BiTreeNode):      def __init__(self, data):          BiTreeNode.__init__(self, data)          self.bf = 0    class AVLTree(BST):      def __init__(self, li=None):          BST.__init__(self, li)        def rotate_right(self, p, c):          s2 = c.rchild          p.lchild = s2          if s2:              s2.parent = p          c.rchild = p          p.parent = c            p.bf = 0          c.bf = 0

AVL插入——右旋-左旋

　　不平衡是由於對K的右孩子的左子樹插入導致的：右旋-左旋

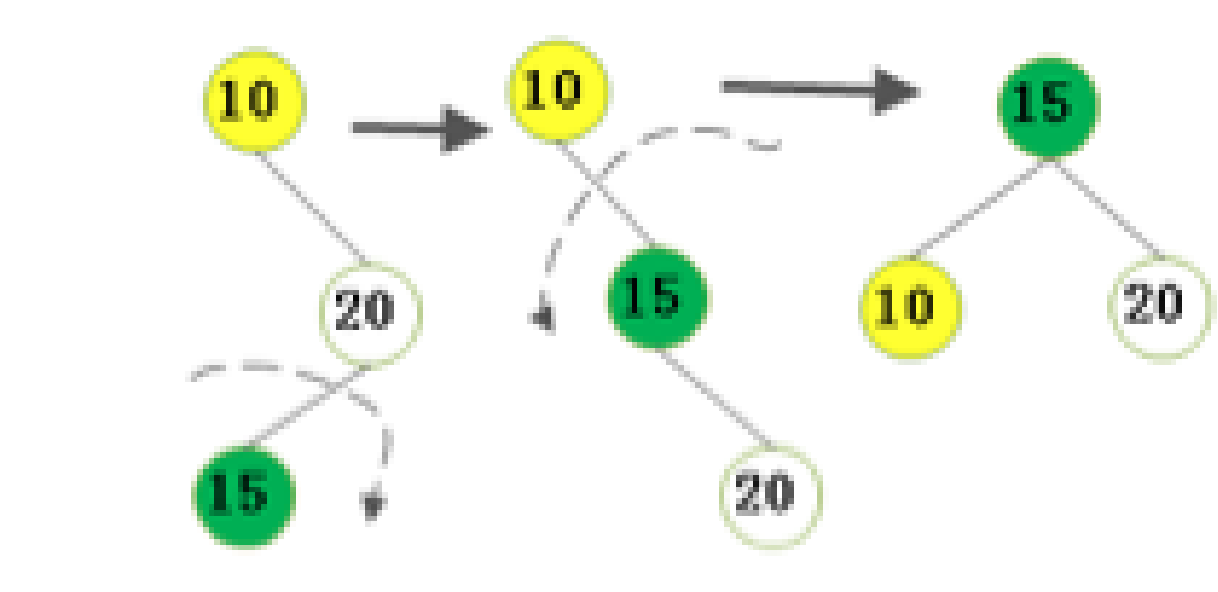
　　右旋左旋的代碼流程如圖所示：

　　代碼如下：

#_*_coding:utf-8_*_  from bst import BiTreeNode, BST      class AVLNode(BiTreeNode):      def __init__(self, data):          BiTreeNode.__init__(self, data)          self.bf = 0    class AVLTree(BST):      def __init__(self, li=None):          BST.__init__(self, li)          def rotate_right_left(self, p, c):          g = c.lchild            s3 = g.rchild          c.lchild = s3          if s3:              s3.parent = c          g.rchild = c          c.parent = g            s2 = g.lchild          p.rchild = s2          if s2:              s2.parent = p          g.lchild = p          p.parent = g            # 更新bf          if g.bf > 0:              p.bf = -1              c.bf = 0          elif g.bf < 0:              p.bf = 0              c.bf = 1          else :  # 插入的是g              p.bf = 0              c.bf = 0

AVL插入——左旋-右旋

　　還有一種不平衡是由於對K的左孩子的右子樹插入導致的：左旋-右旋

　　代碼的流程如下：

　　代碼如下：

#_*_coding:utf-8_*_  from bst import BiTreeNode, BST      class AVLNode(BiTreeNode):      def __init__(self, data):          BiTreeNode.__init__(self, data)          self.bf = 0    class AVLTree(BST):      def __init__(self, li=None):          BST.__init__(self, li)        def rotate_left_right(self, p, c):          g = c.rchild            s2 = g.lchild          c.rchild = s2          if s2:              s2.parent = c          g.lchild = c          c.parent = g            s3 = g.rchild          p.lchild = s3          if s3:              s3.parent = p          g.rchild = p          p.parent = g            # 更新bf          if g.bf < 0:              p.bf = 1              c.bf = 0          elif g.bf > 0:              p.bf = 0              c.bf = -1          else:              p.bf = 0              c.bf = 0

AVL樹的刪除操作

　　刪除操作比較複雜。

　　1，當前節點為要刪除的節點且是樹葉（無子樹），直接刪除，當前節點（為None）的平衡不受影響。

　　2.當前節點為要刪除的節點且只有一個左兒子或右兒子，用左兒子或右兒子代替當前節點，當前節點的平衡不受影響。

　　3.當前節點為要刪除的節點且有左子樹右子樹:如果右子樹高度較高，則從右子樹選取最小節點，將其值賦予當前節點，然後刪除右子樹的最小節點。如果左子樹高度較高，則從左子樹選取最大節點，將其值賦予當前節點，然後刪除左子樹的最大節點。這樣操作當前節點的平衡不會被破壞。

　　4.當前節點不是要刪除的節點，則對其左子樹或者右子樹進行遞歸操作。當前節點的平衡條件可能會被破壞，需要進行平衡操作。

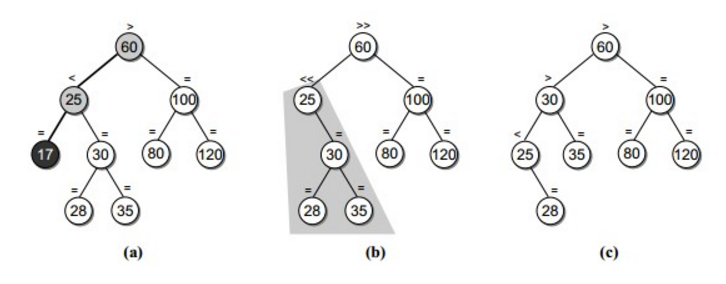
　　如上圖，25為當前節點，左子樹刪除17後平衡條件被破壞，需要根據當前節點(25)的右子樹(30)的左子樹(28)高度是否高於右子樹(35)的高度進行判斷，若高於，進行雙旋轉，否則進行單旋轉。

二叉搜索樹的擴展應用——B樹

　　B樹（B-Tree）：B 樹是一顆自平衡的多路搜索樹，常用語數據庫的索引。

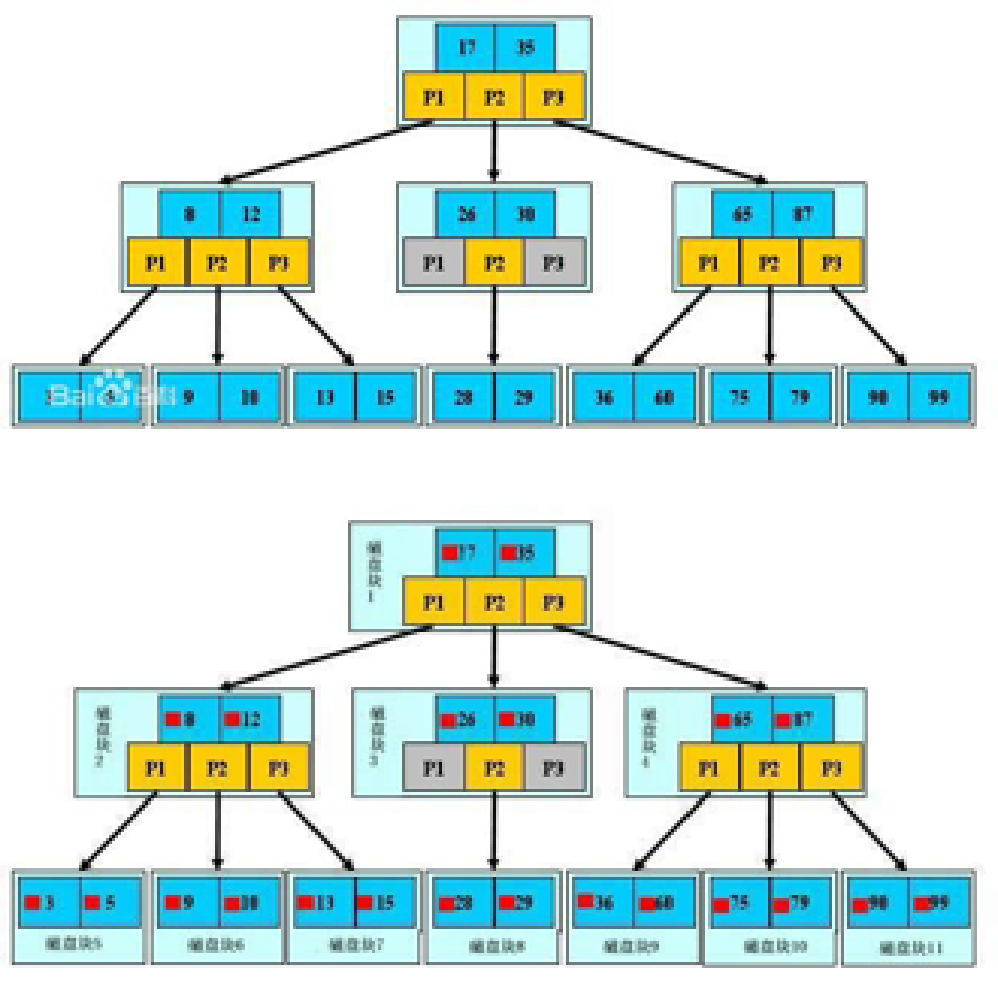
6，二叉樹的圖形化顯示

6.1 在線生成 bst 樹和 avl 樹

　　學習過程中難免遇到理解的問題：圖形化能很好的幫助我們理解問題，下面是兩個在線生成二叉樹的網址，根據自己需要看看，添加

6.2 程序自己生成二叉樹

　　利用PyGraphviz模塊畫出二叉樹

　　參考網址：http://pygraphviz.github.io/documentation/pygraphviz-1.5/ 這裡有詳細的使用說明

安　　裝該模塊失敗，參考這篇博客 https://blog.csdn.net/chirebingxue/article/details/50393755

　　使用了該模塊以完成最後生成的二叉樹顯示，代碼如下

import pygraphviz as pgv      def draw(self, filename='./tree.png'):          g = pgv.AGraph(strict=False, directed=True)          g.node_attr['shape'] = 'circle'            def traver(node):              if node:                  if not node.parent:                      g.add_node(node.key)                  else:                      g.add_edge(node.parent.key, node.key)                  traver(node.left)                  traver(node.right)          traver(self.root)          g.layout('dot')          g.draw(filename)

　　簡單的測試改模塊的效果

tree = AVLTree()  tree.insert(range(0, 20, 2))  # 自己簡單實現了個可以接受一個可迭代對象的數值的插入  tree.draw()  tree.delete_key(14)  tree.draw('tree2.png')

　　最後生成下面的PNG圖

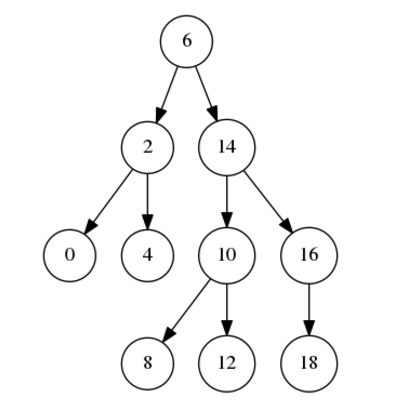
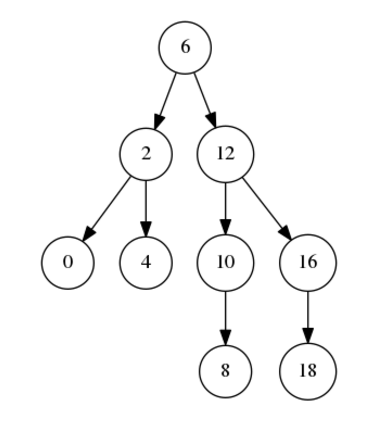
參考文獻：樹：https://www.cnblogs.com/hwnzy/p/11118942.html

二叉搜索樹：https://www.cnblogs.com/lliuye/p/9118591.html

AVL樹：https://www.cnblogs.com/yscl/p/10077607.html