聲學回聲消除(Acoustic Echo Cancellation)原理與實現

• 2019 年 10 月 19 日
• 筆記

　　回聲就是聲音信號經過一系列反射之後，又聽到了自己講話的聲音，這就是回聲。一些回聲是必要的，比如劇院里的音樂回聲以及延遲時間較短的房間回聲；而大多數回聲會造成負面影響，比如在有線或者無線通信時重複聽到自己講話的聲音（回想那些年我們開黑打遊戲時，如果其中有個人開了外放，他的聲音就會回蕩來回蕩去）。因此消除回聲的負面影響對通信系統是十分必要的。

　　針對回聲消除（Acoustic Echo Cancellation，AEC ）問題，現如今最流行的算法就是基於自適應濾波的回聲消除算法。本文從回聲信號的兩種分類以及 AEC 的基本原理出發，介紹幾種經典的 AEC 算法並對其性能進行闡釋。

回聲分類

　　在通信系統中，回聲主要分為兩類：電路回聲和聲學回聲

電路回聲

　　電路回聲通常產生於有線通話中，而造成電路回聲的根本原因是轉換混合器的二線-四線阻抗不能完全匹配。中心局至轉換混合器之間採用四線的連接方式傳輸信號，上面兩條線路用於發送給用戶端信號，下面兩條線路用於接收用戶端信號。通信公司為了降低遠距離信號傳輸成本，將混合器至用戶端的連接線減少為二線連接，分別用於用戶端信號的接受與發送。中間的轉換混合電路功能是將四線連接轉換為二線連接，由於在轉換過程中使用了不同型號的電線或者負載線圈沒有被使用的原因，不可避免地會產生阻抗不匹配現象，導致混合器接收線路上的語音信號流失到了發送線路，產生了回聲信號，使得另一端的用戶在接收信號的同時聽到了自己的聲音。

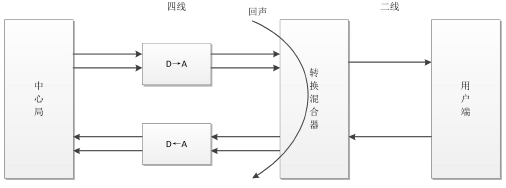
電路回聲產生原理

　　在現如今的數字通信網絡中，轉換混合器與數模轉換器融為一體，但無論是模擬電子線路還是數字電子線路，二-四線的轉換都會造成阻抗不匹配問題，從而導致其產生電路回聲，影響現代通信質量。由於電路回聲的線性以及穩定性，用一個簡單的線性疊加器就可以實現電路回聲消除。首先將產生的回聲信號在數值上取反，線性地疊加在回聲信號上，將產生的回聲信號抵消，實現電路回聲的初步消除。然而由於技術缺陷，線性疊加器不能完整地將回聲信號抹去，因此需要添加一個非線性處理器，其實質是一個阻擋信號的開關，將殘餘的回聲信號經過非線性處理之後，就可以實現電路回聲的消除，或者得到噪聲很小的靜音信號。由於電路回聲信號是線性且穩定的，所以比較容易將其消除，而本文主要研究的是如何消除非線性的聲學回聲。

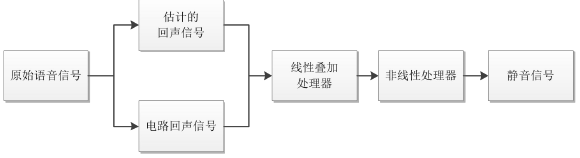
電路回聲消除的基本原理

聲學回聲

　　在麥克風與揚聲器互相作用影響的雙工通信系統中極易產生聲學回聲。如下圖所示

遠端講話者A–>麥克風A–>電話A–>電話B—->揚聲器B—>麥克風B–>電話B–>電話A–>揚聲器A—>麥克風A—>………就這樣無限循環，

詳細講解：遠端講話者A的話語被麥克風采集並傳入至通信設備，經過無線或有線傳輸之後達到近端的通信設備，並通過近端 B 的揚聲器播放，這個聲音又會被近端 B 的麥克風拾取至其通信設備形成聲學回聲，經傳輸又返回了遠端 A 的通信設備，並通過遠端 A 的揚聲器播放出來，從而遠端講話者就聽到了自己的回聲。

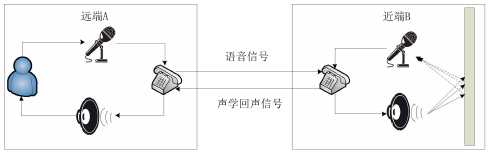
聲學回聲產生原理

聲學回聲信號根據傳輸途徑的差別可以分別直接回聲信號和間接回聲信號。

直接回聲：近端揚聲器B將語音信號播放出來後，近端麥克風B直接將其採集後得到的回聲。

　　直接回聲不受環境的印象，與揚聲器到麥克風的距離及位置有很大的關係，因此直接回聲是一種線性信號。

間接回聲：近端揚聲器B將語音信號播放出來後，語音信號經過複雜多變的牆面反射後由近端麥克風B將其拾取。

　　間接回聲的大小與房間環境、物品擺放以及牆面吸引係數等等因素有關，因此間接回聲是一種非線性信號。

回聲消除技術主要用於在免提電話、電話會議系統等情形中。

AEC的基本原理

　　如今解決 AEC 問題最常用的方法，就是

使用不同的自適應濾波算法調整濾波器的權值向量，估計一個近似的回聲路徑來逼近真實回聲路徑，從而得到估計的回聲信號，並在純凈語音和回聲的混合信號中除去此信號來實現回聲的消除。

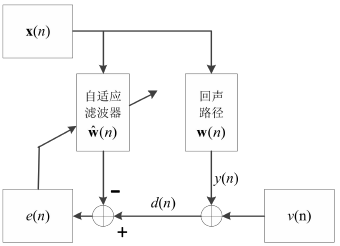
 AEC的基本原理

　　$x(n)$為遠端輸入信號，經過未知的回聲路徑$w(n)$得到$y(n)=x(n)*w(n)$，再加上觀測噪聲$v(n)$即為期望信號$d(n)= y(n) + v(n)$。x(n)通過自適應濾波器$hat{w}(n)$得到估計的回聲信號，並與期望信號$d(n)$相減得到誤差信號$e(n)$，即$e(n)=d(n)-hat{w}^T(n)x(n)$，誤差信號的值越小說明自適應濾波算法所估計的回聲路徑就越接近實際的回聲路徑。

　　濾波器採用特定的自適應算法不停地調整權值向量，使估計的回聲路徑 hat{w}(n) 逐漸趨近於真實回聲路徑$w(n)$。顯然，在 AEC 問題中，自適應濾波器的選擇對回聲消除的性能好壞起着十分關鍵的作用。

自適應濾波器的基本原理

　　自適應濾波器是一個對輸入信號進行處理並不停學習，直到其達到期望值的器件。自適應濾波器在輸入信號非平穩條件下，也可以根據環境不斷調節濾波器權值向量，使算法達到特定的收斂條件，從而實現自適應濾波過程。

　　自適應濾波器按輸入信號類型可分為模擬濾波器和離散濾波器，本文中使用的是離散濾波器中的數字濾波器（數字濾波器按結構可劃分為輸入不僅與過去和當前的輸入有關、還與過去的輸出有關的無限衝激響應濾波器（IIR），以及輸出與有限個過去和當前的輸入有關的有限衝激響應濾波器（FIR））為了使得自適應濾波器具有更強的穩定性，並且具有足夠的濾波器係數可以用來調整以達到特定的收斂準則，一般選取橫向的 FIR 濾波器進行來進行回聲的消除

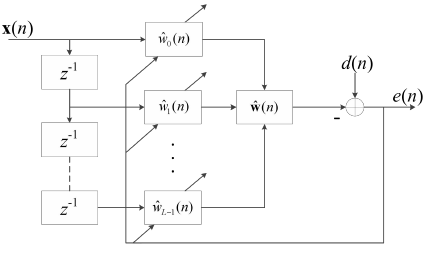
 橫向FIR濾波器結構框圖

　　$x(n)$是遠端輸入信號，$hat{w}_i(n)$是濾波器係數，其中$i=0,1,…,L-1$，$L$為濾波器的長度，$n$為採樣點數，$hat{w}(n)$為濾波器的權值向量且$hat{w}(n)=[hat{w}_0(n),hat{w}_1(n),…,hat{w}_{L-1}(n)]^T$，根據誤差信號$e(n)=d(n)-hat{w}^T(n)x(n)$的值以及不同算法的收斂準則調整濾波器的權值向量。

　　然而自適應濾波算法的選擇從根本上決定了回聲消除的效果是否良好，接下來將介紹幾種解決 AEC 問題的經典自適應濾波算法。

回聲消除常用算法

LSM算法

　　通過上面AEC的基本原理我們知道了誤差信號$e(n)$等於期望信號減去濾波器輸出信號：

$$e(n)=d(n)-hat{w}^T(n)x(n)$$

對上式兩端先平方，然後再求其數學期望，可將$e(n)$的MSE表示為：

$$xi=E[e^2(n)]=E[d^2(n)]-2P^That{w}(n)+hat{w}^T(n)Rhat{w}(n)$$

其中，$P=E[d(n)x(n)]$為$d(n)$與輸入信號$x(n)$的負相關矩陣，$R=E[x(n)x^T(n)]$為$x(n)$的自相關矩陣。

　　對誤差信號求導並且使導數值置零，求解得到使得誤差最小的“最優權重” $hat{w}_{opt}(n)=frac{P}{R}$，R 和 P 的估計分別為$hat{R}(n) 和$hat{P}(n)$ ，利用各自的瞬時估計值將其分別表示為：hat{R}(n)=x(x)x^T(n)；hat{P}(n)=d(n)x(n) 。另外，用$hat{g}_w(n)$表示誤差信號對權值向量導數的估計值，利用下式方法求解最優權值向量的維納解：

 得到：$hat{g}_w(n)=-2e(n)x(n)$ ，算法取瞬時平方誤差作為目標函數，那麼$hat{g}_w(n)$為其真實梯度，因為：

因此得到 LMS 算法的權值向量更新公式：

$$hat{w}(n+1)=hat{w}(n)+2mu e(n)x(n)$$

式中，$mu$為固定步長因子，$mu$的大小很大程度上決定了算法的收斂與穩態性能。LMS 算法複雜性低，但是它的收斂速度慢。為改善 LMS 這個不足之處，科研人員提出一系列改進算法，NLMS 算法就是其中一種

NLMS算法

NSAF算法

WebRTC算法

本文講解WebRTC的matlab梳理，由於matlab代碼和webRTC的c++代碼命名幾乎一致。所以c++的實現就一筆帶過。

RERL-residual_echo_return_loss
ERL-echo return loss
ERLE echo return loss enhancement
NLP non-linear processing

% 首先matlab讀入遠端和近端信號  % near.pcm 是麥克風捕捉到的信號  fid=fopen('near.pcm', 'rb'); % 加載far端  ssin=fread(fid,inf,'float32');  fclose(fid);  % far.pcm 是揚聲器播放的音樂  fid=fopen('far.pcm', 'rb'); % 加載near端  rrin=fread(fid,inf,'float32');  fclose(fid);    % ------- 對變量賦初始值 -----------  fs=16000;  NLPon=1;     % 非線性處理 on  M = 16;     % 分區數  N = 64;     % 分區長度  L = M*N;     % 濾波器長度  VADtd=48;  alp = 0.15; % 功率估計因子  alc = 0.1;     % 相干估計因子  step = 0.1875;%0.1875; 下台階尺寸 Downward step size    len=length(ssin);  NN=len;  Nb=floor(NN/N)-M;  % Nb=麥克風采集到的數據塊數-16(分區數)  % 這是因為第一次輸入了16塊，所以這裡減掉了16  for kk=1:Nb      pos = N * (kk-1) + start;    % pos是每一次添加一塊時的地址指針      %far is speaker played music      xk = rrin(pos:pos+N-1);      %near is micphone captured signal      dk = ssin(pos:pos+N-1);

 明天繼續寫

參考

《基於自適應濾波器的聲學回聲消除研究——馮江浩》