第一次作業:深度學習基礎
第一次作業:深度學習基礎
經過了第一周的學習,對深度學習有了系統的認識。
- 視頻學習
- 1.1 緒論
- 1.2 深度學習概述
- 1.3 pytorch基礎
- 代碼練習
- 2.1 螺旋數據分類
- 2.2 回歸分析
1. 視頻學習
通過視頻學習整理出以下知識點,做好理論儲備。
1.1 緒論
AI誕生:1956年美國達特茅斯會議:人工智能 (Artificial Intelligence) 概念誕生。
圖靈測試(英語:Turing test,又譯圖靈試驗)是圖靈於1950年提出的一個關於判斷機器是否能夠思考的著名思想實驗,測試某機器是否能表現出與人等價或無法區分的智能。測試的談話僅限於使用唯一的文本管道,例如計算機鍵盤和屏幕,這樣的結果不依賴於計算機把單詞轉換為音頻的能力。
——維基百科
關係:人工智能>機器學習>深度學習

機器學習應用領域:
計算機視覺(CV)、語音識別、自然語言處理(NLP)
計算機視覺應用:圖像分類、目標檢測、語義分割等
機器學習三要素:
- 模型:問題建模、確定假設空間
- 策略:確定目標函數
- 算法:求解模型參數
對於模型的分類:
- 數據標記:監督學習模型、無監督學習模型(半監督學習模型、強化學習模型)
- 數據分佈:參數模型、非參數模型
- 建模對象:判別模型、生成模型
知識工程(專家系統) vs 機器學習(神經網絡)
知識圖譜(符號主義) vs 深度學習(連接主義)

機器學習模型:

人工智能的發展:
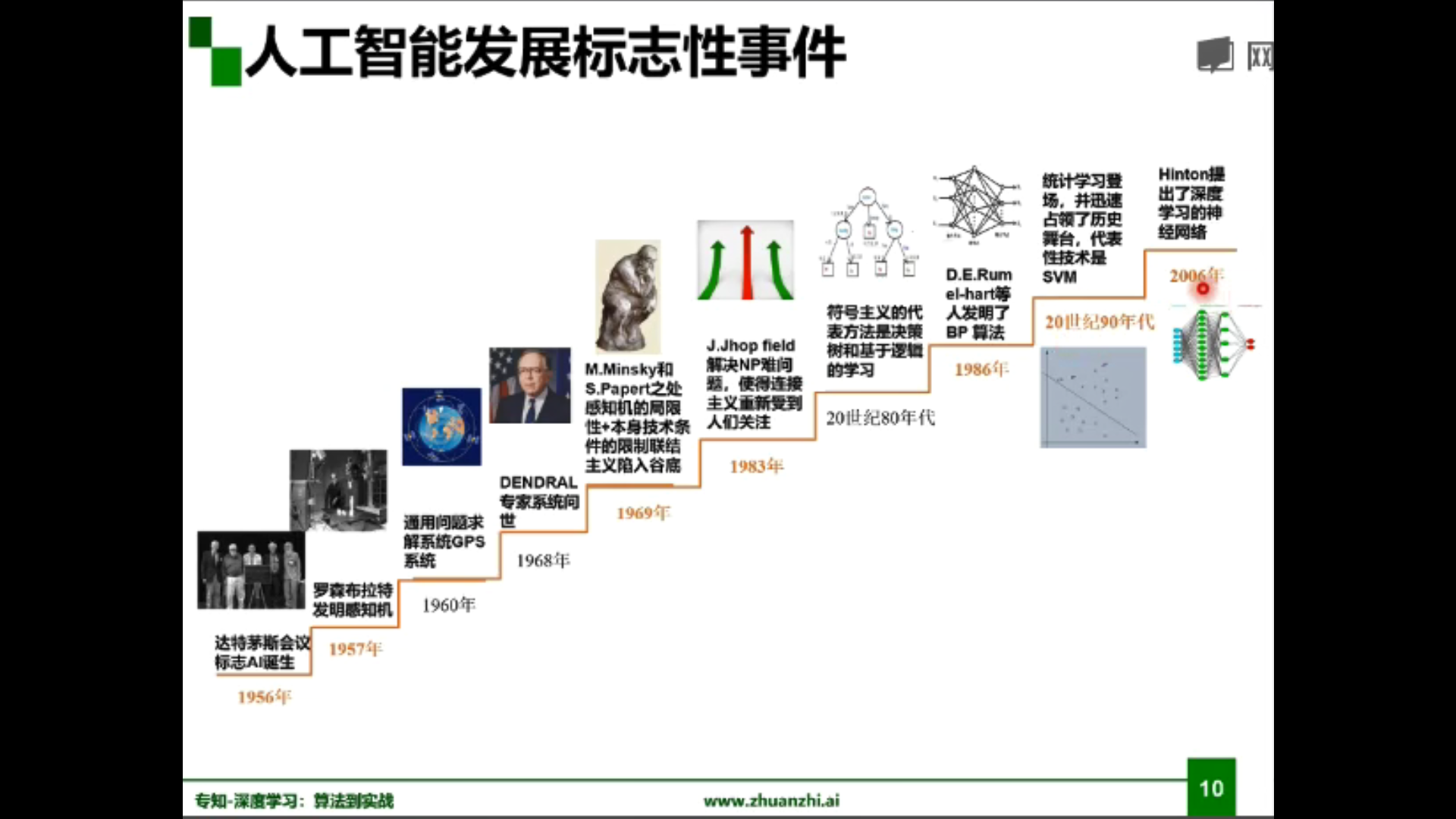
標誌性人物:
| 名稱 | 事件 |
|---|---|
| Rosenblatt | 提出感知機(Perceptron) |
| Minsky | 論證了感知機的局限(異或門與計算量) |
| Rumelhart | 闡述BP反向傳播算法及其應用 |
| Yann Lecun | 運用卷積神經網絡(CNN) |
| Geoffrey Hinton | 堅守神經網絡研究,並改名深度學習(Deep Learning),發表深度置信網絡(DBN)並使用限制玻爾茲曼機(RBM)學習 |
| Andrew Ng | 使用GPU加快運行速度 |
| 李飛飛 | 宣布建立超大型圖像數據庫ImageNet,ILSVRC競賽成為技術突破的轉折點 |
| Yoshua Bengio | 使用修正線性單元(ReLU)作為激勵函數 |
| Schmidhuber | 提出了長短期記憶(LSTM)的計算模型 |
| Ian Goodfellow | 提出生成式對抗網絡(GANs) |
2019年圖靈獎:Geoffrey Hinton, Yann LeCun,和Yoshua Bengio
1.2 深度學習概述
神經網絡結構的發展:
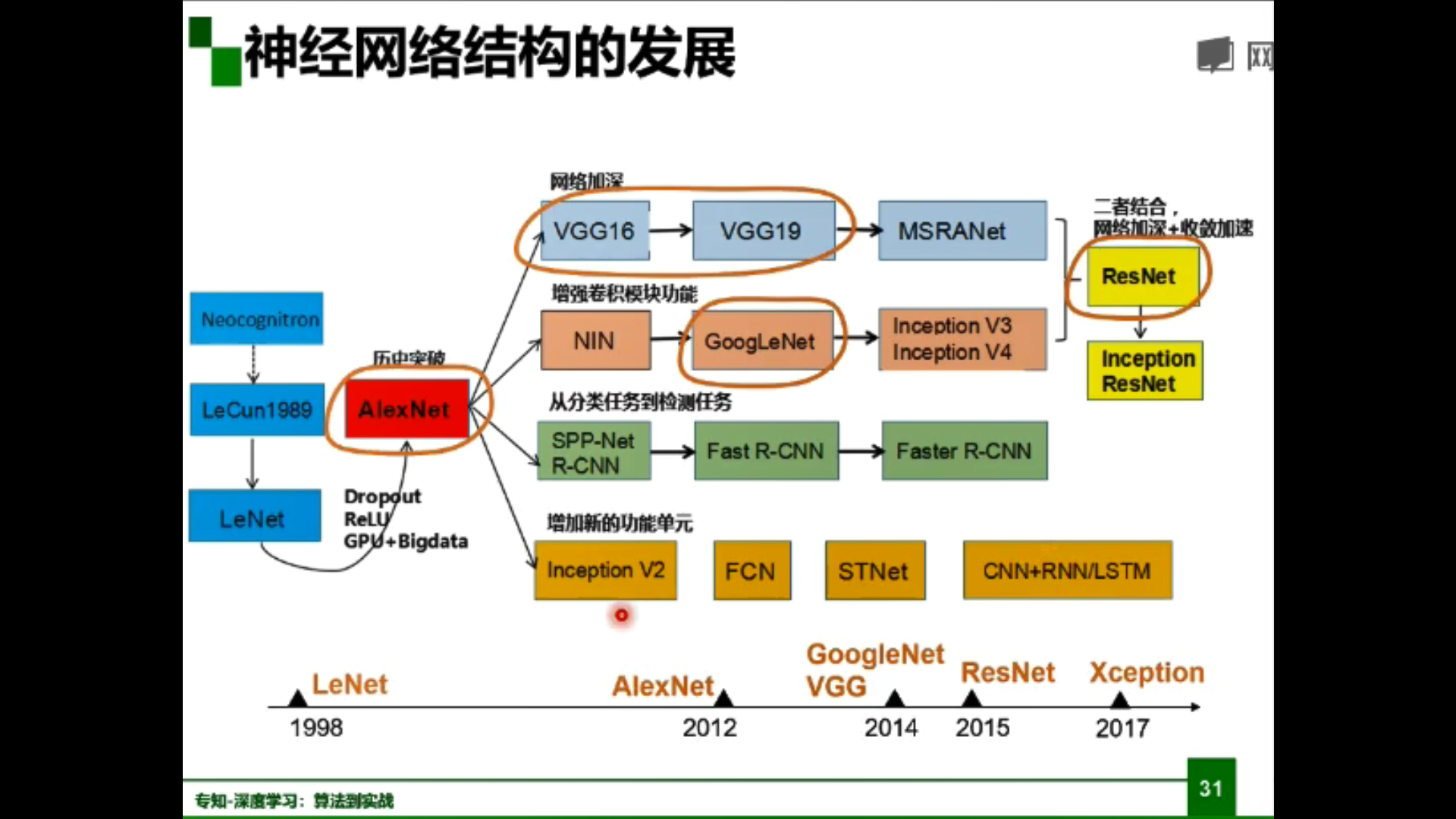
深度學習三個助推劑:大數據、算法、計算力
深度學習的局限性:
線性回歸、決策樹、SVM、隨機森林、深度學習,從左往右準確性(泛化性)遞增,解釋性遞減。

M-P神經元:
M-P神經元由McCulloch與Pitts發現並命名,作為神經網絡的基本單位。
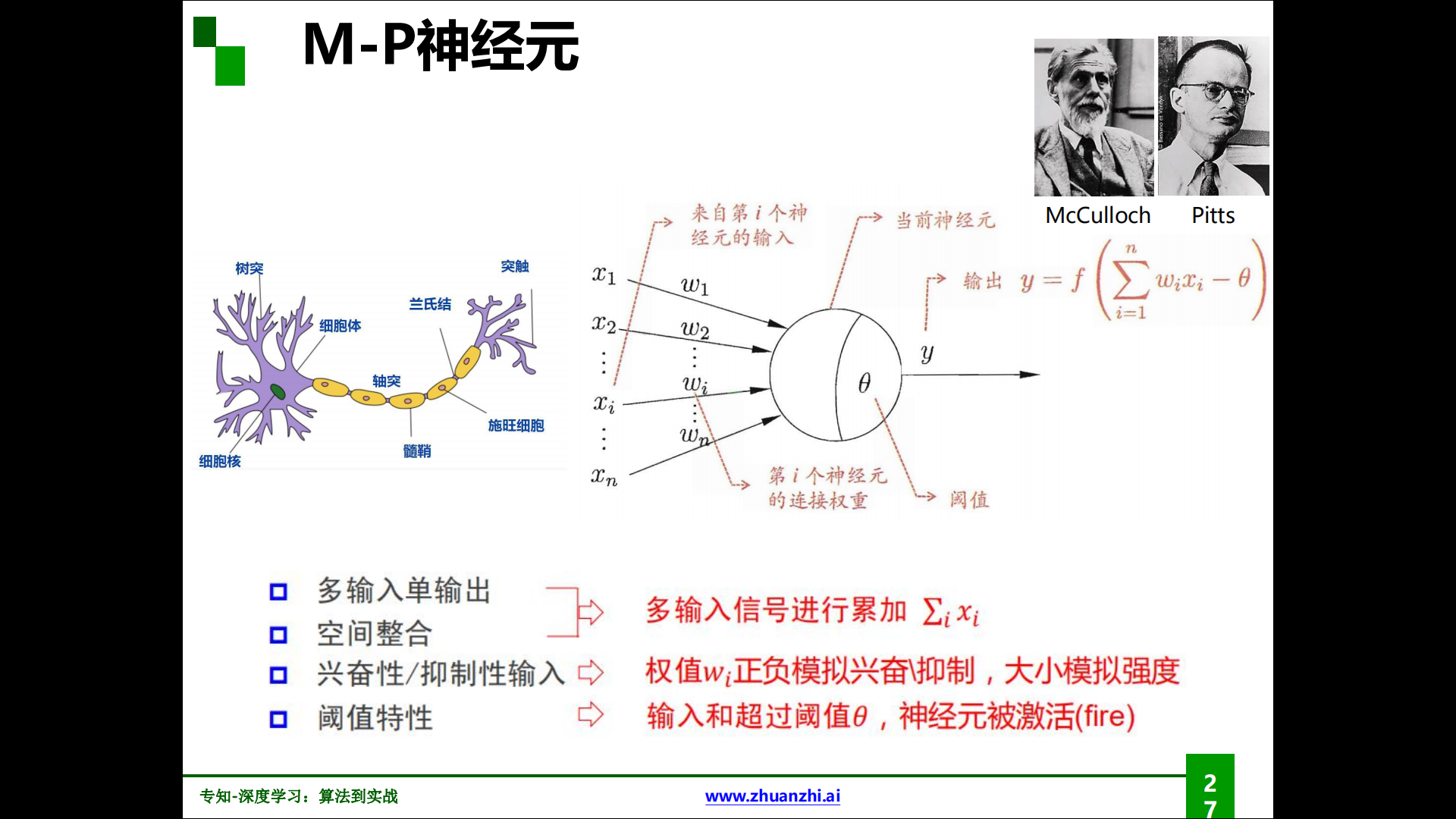
各種激活函數:
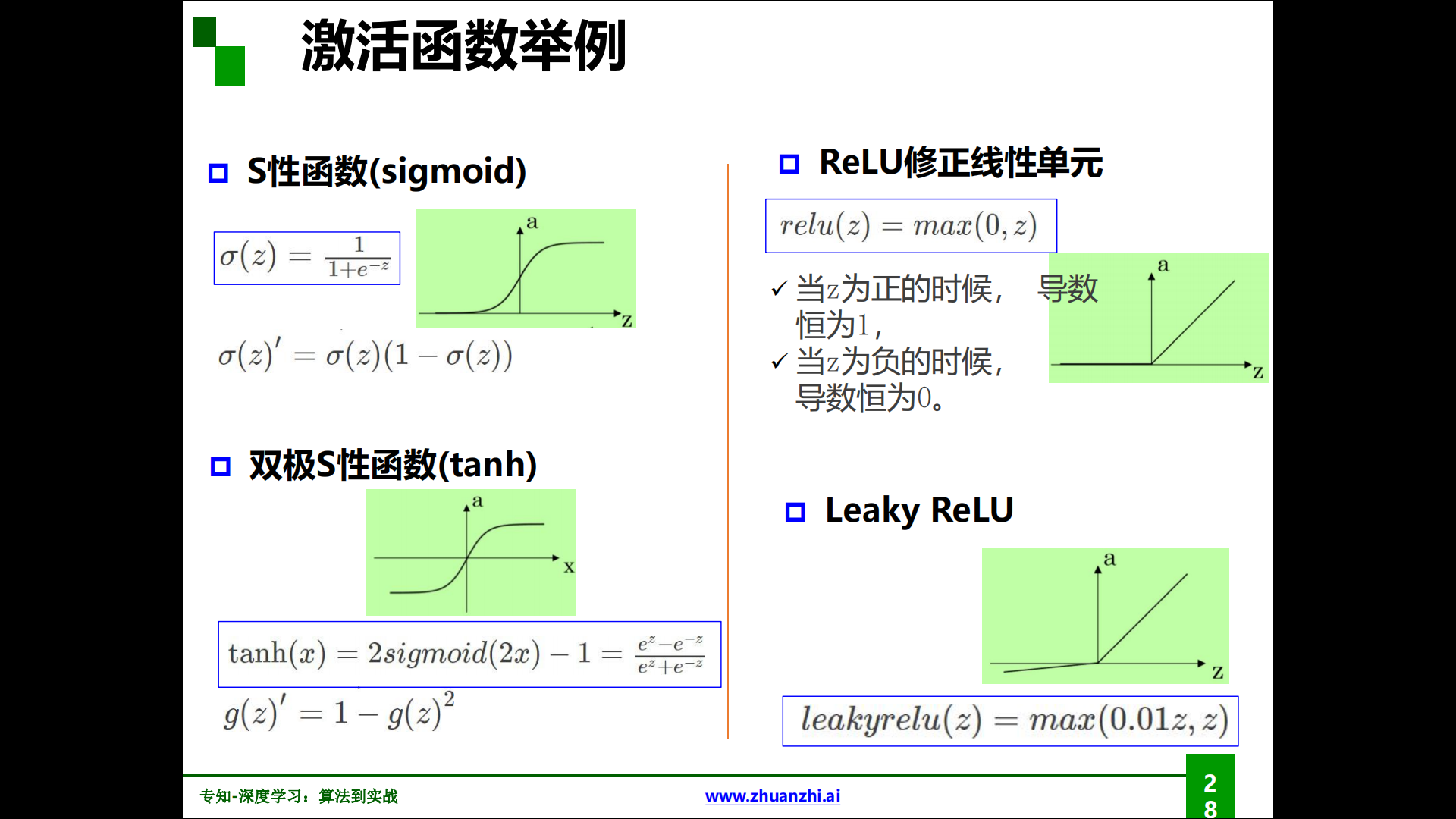
萬有逼近定理:
- 如果一個隱層包含足夠多的神經元,三層前饋神經網絡(輸入-隱層-輸出)能以任意精度逼近任意預定的連續函數。
- 當隱層足夠寬時,雙隱層感知器(輸入-隱層1-隱層2-輸出)可以逼近任意非連續函數:可以解決任何複雜的分類問題。
為什麼線性分類任務組合後可以解決非線性分類任務?
答:第一層感知器經過空間變換將非線性問題轉化為線性問題。
| 結構 | 決策區域類型 |
|---|---|
| 無隱層 | 由一超平面分成兩個 |
| 單隱層 | 開凸區域或閉凸區域 |
| 雙隱層 | 任意形狀(複雜度由單元數目確定) |
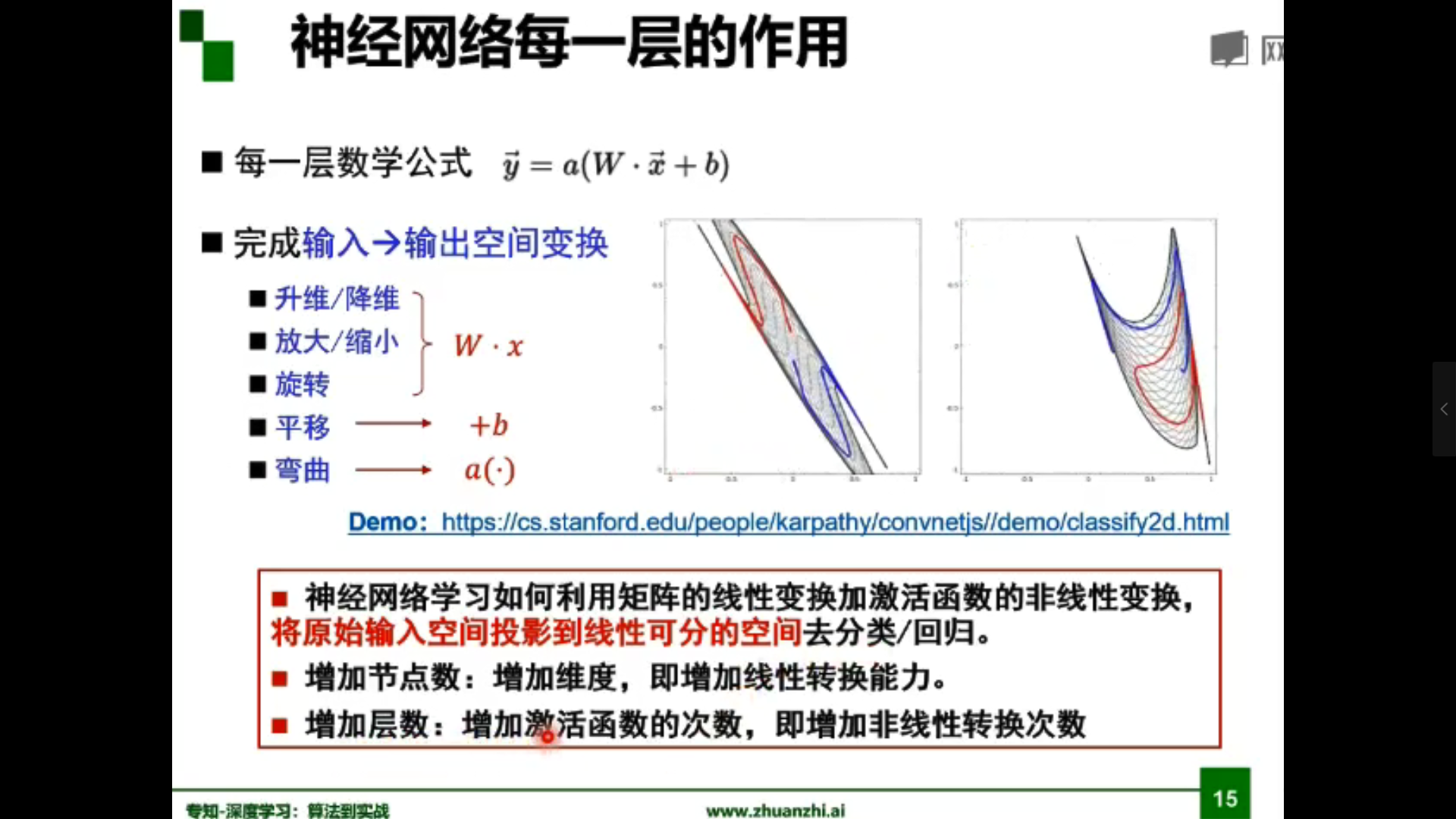
-
梯度:一個向量。方向是最大方嚮導數的方向。模為方嚮導數的最大值。
-
梯度下降:參數沿負梯度方向更新可以使函數值下降。
-
反向傳播:根據損失函數計算的誤差通過反向傳播的方式,指導深度網絡參數的更新優化。
為什麼使用梯度下降來優化神經網絡參數?
我們的目的是讓損失函數取得極小值。所以就變成了一個尋找函數最小值的問題,在數學上,很自然的就會想到使用梯度下降來解決。
深度學習兩個優化器:Adam、SGD(隨機梯度下降)
一般Adam效果較好。
梯度消失、爆炸會帶來哪些影響?
舉個例子,對於一個含有三層隱藏層的簡單神經網絡來說,當梯度消失發生時,接近於輸出層的隱藏層由於其梯度相對正常,所以權值更新時也就相對正常,但是當越靠近輸入層時,由於梯度消失現象,會導致靠近輸入層的隱藏層權值更新緩慢或者更新停滯。這就導致在訓練時,只等價於後面幾層的淺層網絡的學習。
神經網絡的第三次興起:
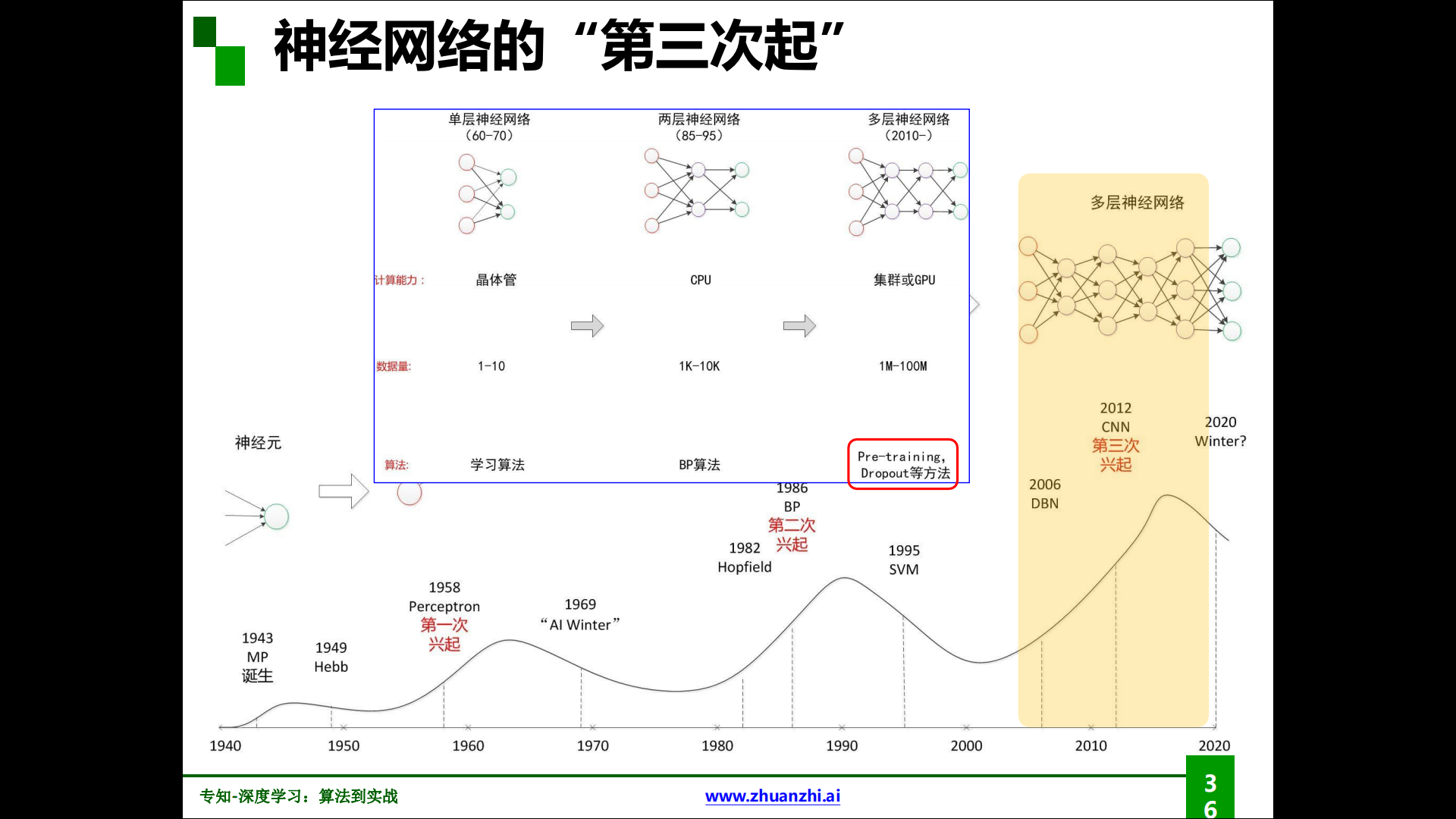
解決梯度消失的方法:

逐層預訓練(layer-wise pre-training):權重初始化,擁有一個較好的初始值,儘可能避免局部極小值梯度消失。
- 受限玻爾茲曼機(RBM)
- 自編碼器(Autoencoder)
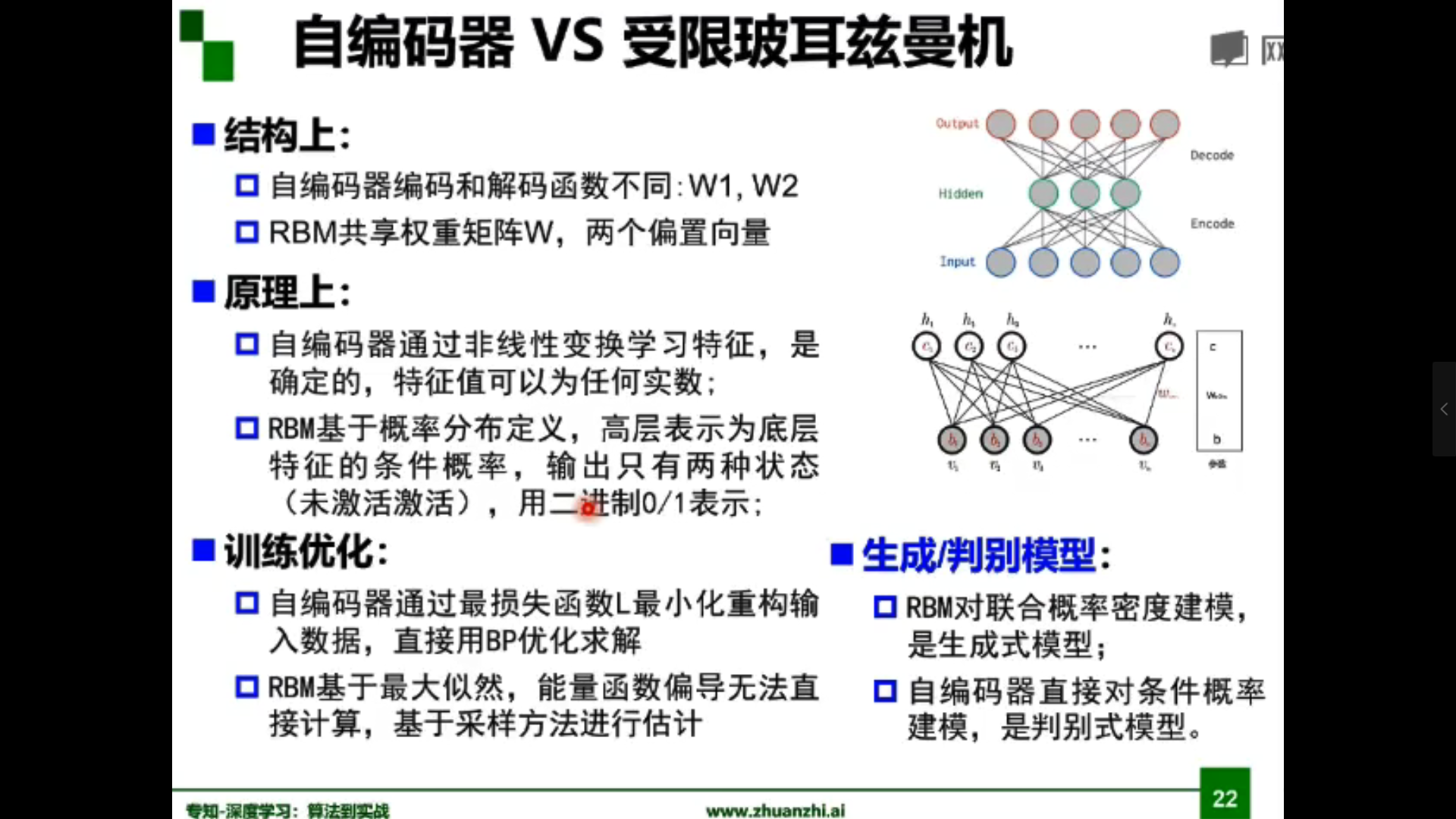
自編碼器原理:
假設輸出與輸入相同(target=input),是一種儘可能復現輸入信號的神經網絡。通過調整encoder和decoder的參數,使得重構誤差最小。
自編碼器可實現降維、去噪

微調(fine-tune)
1.3 pytorch基礎
- torch.Tensor(張量,各種類型數據的封裝)
- data屬性,用來存數據
- grad屬性,用來存梯度
- grad_fn,用來指向創造自己的Function
- torch.autograd.Function(函數類,定義在Tensor類上的操作)
如何用Pytorch完成實驗?
- 加載、預處理數據集
- 構建模型
- 定義損失函數
- 實現優化算法
- 迭代訓練
- 加速計算(GPU)
- 存儲模型
- 構建baseline
2. 代碼練習
理論指導實踐,這裡引入中國海洋大學視覺實驗室前沿理論小組 pytorch 學習中03分類問題(離散性)、04回歸問題(連續性)兩個經典的範例,通過Colaboratory運行代碼觀察結果,並寫下一點自己的理解。
在訓練模型時,如果訓練數據過多,無法一次性將所有數據送入計算,那麼我們就會遇到epoch,batchsize,iterations這些概念。為了克服數據量多的問題,我們會選擇將數據分成幾個部分,即batch,進行訓練,從而使得每個批次的數據量是可以負載的。將這些batch的數據逐一送入計算訓練,更新神經網絡的權值,使得網絡收斂。
一個epoch指代所有的數據送入網絡中完成一次前向計算及反向傳播的過程。
所謂Batch就是每次送入網絡中訓練的一部分數據,而Batch Size就是每個batch中訓練樣本的數量
iterations就是完成一次epoch所需的batch個數。
問題:
- 神經網絡的輸出層需要激活函數嗎?
2.1 螺旋數據分類
這裡有三點需要注意:
每一次反向傳播前,都要把梯度清零:當GPU顯存較少時,又想要調大batch-size,此時就可以利用PyTorch默認進行梯度累加的性質來進行backward。
梯度累加就是,每次獲取1個batch的數據,計算1次梯度,梯度不清空,不斷累加,累加一定次數後,根據累加的梯度更新網絡參數,然後清空梯度,進行下一次循環。
一定條件下,batchsize越大訓練效果越好,梯度累加則實現了batchsize的變相擴大,如果accumulation_steps為8,則batchsize ‘變相’ 擴大了8倍,是我們這種乞丐實驗室解決顯存受限的一個不錯的trick,使用時需要注意,學習率也要適當放大。
——知乎Pascal
加入ReLU激活函數,分類的準確率顯著提高:非線性變換。
為什麼激活函數是非線性的?如果不用激勵函數(相當於激勵函數是f(x)=x),在這種情況下,每一層的輸出都是上一層的線性函數,無論神經網絡有多少層,輸出都是輸入的線性組合,這與一個隱藏層的效果相當(這種情況就是多層感知機MPL)。但當我們需要進行深度神經網絡訓練(多個隱藏層)的時候,如果激活函數仍然使用線性的,多層的隱藏函數與一層的隱藏函數作用的相當的,就失去了深度神經網絡的意義,所以引入非線性函數作為激活函數。
一般在描述神經網絡層數時不包括輸入層。

2.1.1 構建線性模型分類
learning_rate = 1e-3
lambda_l2 = 1e-5
# nn 包用來創建線性模型
# 每一個線性模型都包含 weight 和 bias
model = nn.Sequential(
nn.Linear(D, H),
nn.Linear(H, C)
)
model.to(device) # 把模型放到GPU上
# nn 包含多種不同的損失函數,這裡使用的是交叉熵(cross entropy loss)損失函數
criterion = torch.nn.CrossEntropyLoss()
# 這裡使用 optim 包進行隨機梯度下降(stochastic gradient descent)優化
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)
# 開始訓練
for t in range(1000):
# 把數據輸入模型,得到預測結果
y_pred = model(X)
# 計算損失和準確率
loss = criterion(y_pred, Y)
score, predicted = torch.max(y_pred, 1)
acc = (Y == predicted).sum().float() / len(Y)
print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))
display.clear_output(wait=True)
# 反向傳播前把梯度置 0
optimizer.zero_grad()
# 反向傳播優化
loss.backward()
# 更新全部參數
optimizer.step()
[EPOCH]: 999, [LOSS]: 0.861541, [ACCURACY]: 0.504
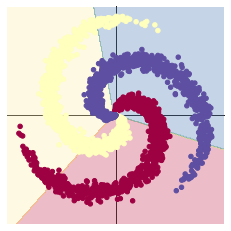
2.1.2 構建兩層神經網絡分類
learning_rate = 1e-3
lambda_l2 = 1e-5
# 這裡可以看到,和上面模型不同的是,在兩層之間加入了一個 ReLU 激活函數
model = nn.Sequential(
nn.Linear(D, H),
nn.ReLU(),
nn.Linear(H, C)
)
model.to(device)
# 下面的代碼和之前是完全一樣的,這裡不過多敘述
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2
# 訓練模型,和之前的代碼是完全一樣的
for t in range(1000):
y_pred = model(X)
loss = criterion(y_pred, Y)
score, predicted = torch.max(y_pred, 1)
acc = ((Y == predicted).sum().float() / len(Y))
print("[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f" % (t, loss.item(), acc))
display.clear_output(wait=True)
# zero the gradients before running the backward pass.
optimizer.zero_grad()
# Backward pass to compute the gradient
loss.backward()
# Update params
optimizer.step()
[EPOCH]: 999, [LOSS]: 0.183681, [ACCURACY]: 0.943
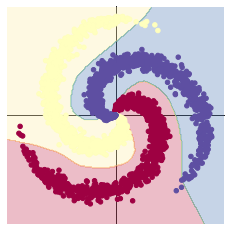
2.2 回歸分析
兩點思考:
對比三類激活函數:
| 函數 | 優點 | 缺點 |
|---|---|---|
| Sigmoid | Sigmoid函數是深度學習領域開始時使用頻率最高的激活函數,它是便於求導的平滑函數,能夠將輸出值壓縮到0-1範圍之內 | 容易出現梯度消失;輸出不是zero-centered;冪運算相對耗時 |
| Tanh | 全程可導;輸出區間為-1到1;解決了zero-centered的輸出問題 | 梯度消失的問題和冪運算的問題仍然存在 |
| ReLU | 解決了梯度消失的問題 (在正區間);計算速度非常快,只需要判斷輸入是否大於0;收斂速度遠快於Sigmoid和Tanh;ReLU會使一部分神經元的輸出為0,這樣就造成了網絡的稀疏性,並且減少了參數的相互依存關係,緩解了過擬合問題的發生 | 輸出不是zero-centered;某些神經元可能永遠不會被激活,導致相應的參數永遠不能被更新(Dead ReLU Problem) |
有兩個主要原因可能導致Dead ReLU Problem:
- 非常不幸的參數初始化,這種情況比較少見
- 學習速率太高導致在訓練過程中參數更新太大,不幸使網絡進入這種狀態
解決方法:可以採用Xavier初始化方法,以及避免將學習速率設置太大或使用adagrad等自動調節學習速率的算法。
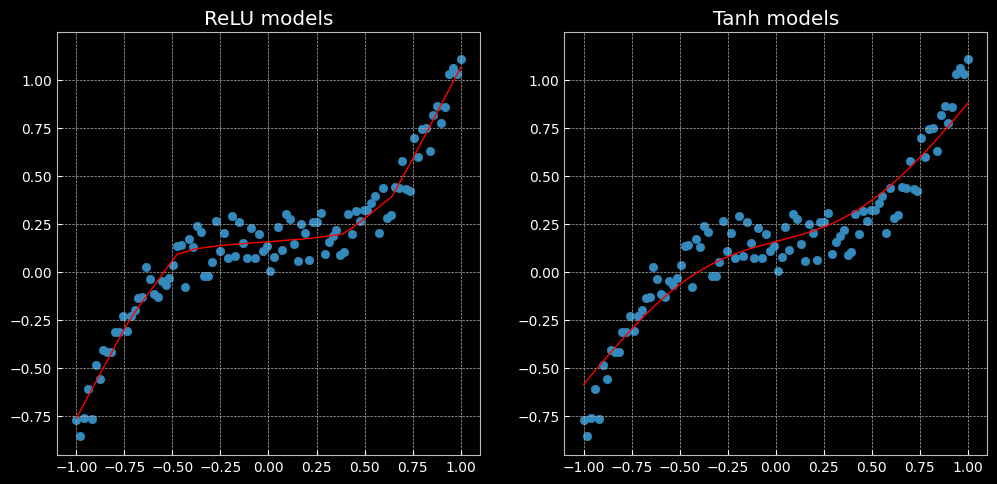
ReLU與Tanh表現效果不同:前者是分段的線性函數,而後者是連續且平滑的回歸。
The former is a piecewise linear function, whereas the latter is a continuous and smooth regression.
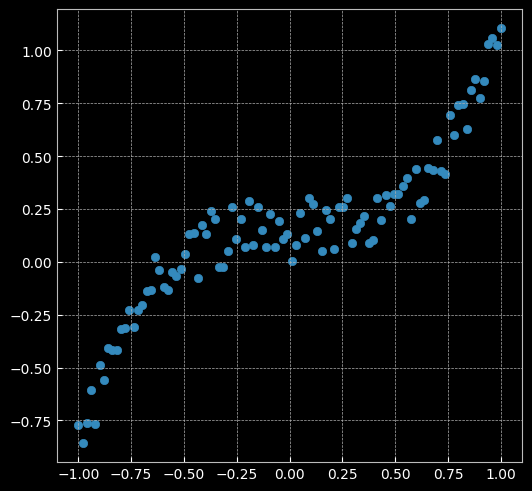
2.2.1 建立線性模型(兩層網絡間沒有激活函數)
learning_rate = 1e-3
lambda_l2 = 1e-5
# 建立神經網絡模型
model = nn.Sequential(
nn.Linear(D, H),
nn.Linear(H, C)
)
model.to(device) # 模型轉到 GPU
# 對於回歸問題,使用MSE損失函數
criterion = torch.nn.MSELoss()
# 定義優化器,使用SGD
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2
# 開始訓練
for t in range(1000):
# 數據輸入模型得到預測結果
y_pred = model(X)
# 計算 MSE 損失
loss = criterion(y_pred, y)
print("[EPOCH]: %i, [LOSS or MSE]: %.6f" % (t, loss.item()))
display.clear_output(wait=True)
# 反向傳播前,梯度清零
optimizer.zero_grad()
# 反向傳播
loss.backward()
# 更新參數
optimizer.step()
[EPOCH]: 999, [LOSS or MSE]: 0.029701
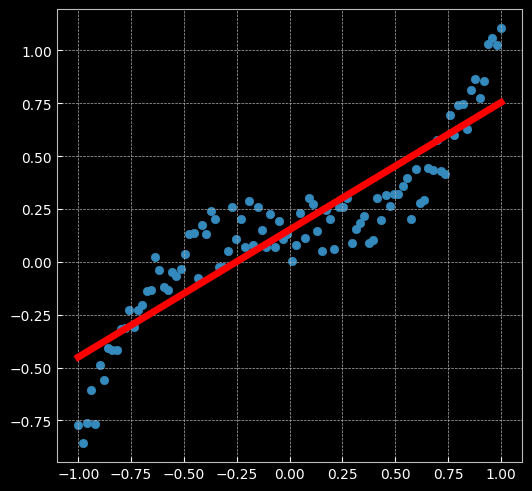
2.2.2 兩層神經網絡
# 這裡定義了2個網絡,一個 relu_model,一個 tanh_model,
# 使用了不同的激活函數
relu_model = nn.Sequential(
nn.Linear(D, H),
nn.ReLU(),
nn.Linear(H, C)
)
relu_model.to(device)
tanh_model = nn.Sequential(
nn.Linear(D, H),
nn.Tanh(),
nn.Linear(H, C)
)
tanh_model.to(device)
# MSE損失函數
criterion = torch.nn.MSELoss()
# 定義優化器,使用 Adam,這裡仍使用 SGD 優化器的化效果會比較差,具體原因請自行百度
optimizer_relumodel = torch.optim.Adam(relu_model.parameters(), lr=learning_rate, weight_decay=lambda_l2)
optimizer_tanhmodel = torch.optim.Adam(tanh_model.parameters(), lr=learning_rate, weight_decay=lambda_l2)
# 開始訓練
for t in range(1000):
y_pred_relumodel = relu_model(X)
y_pred_tanhmodel = tanh_model(X)
# 計算損失與準確率
loss_relumodel = criterion(y_pred_relumodel, y)
loss_tanhmodel = criterion(y_pred_tanhmodel, y)
print(f"[MODEL]: relu_model, [EPOCH]: {t}, [LOSS]: {loss_relumodel.item():.6f}")
print(f"[MODEL]: tanh_model, [EPOCH]: {t}, [LOSS]: {loss_tanhmodel.item():.6f}")
display.clear_output(wait=True)
optimizer_relumodel.zero_grad()
optimizer_tanhmodel.zero_grad()
loss_relumodel.backward()
loss_tanhmodel.backward()
optimizer_relumodel.step()
optimizer_tanhmodel.step()
[MODEL]: relu_model, [EPOCH]: 999, [LOSS]: 0.006584
[MODEL]: tanh_model, [EPOCH]: 999, [LOSS]: 0.014194