python常用算法學習（4）——數據結構

2019 年 10 月 18 日
筆記

數據結構簡介

1，數據結構

　　數據結構是指相互之間存在着一種或多種關係的數據元素的集合和該集合中數據元素之間的關係組成。簡單來說，數據結構就是設計數據以何種方式組織並存貯在計算機中。比如：列表，集合與字典等都是一種數據結構。而之前已經學習過列表，字典，集合，元組等，這裡就簡單說一下不再贅述。

　　N.Wirth：“程序=數據結構+算法”

　　數據：數據即信息的載體，是能夠輸入到計算機中並且能被計算機識別，存儲和處理的符號總稱。

　　數據元素：數據元素是數據的基本單位，又稱之為記錄（Record），一般，數據元素若由若干基本型（或稱字段，域，屬性）組成。

2，數據結構的分類

　　數據結構按照其邏輯結構可分為線性結構，樹結構，圖結構

線性結構：數據結構中的元素存在一對一的相互關係
樹結構：數據結構中的元素存在一對多的相互關係
圖結構：數據結構中的元素存在多對多的相互關係

3，存儲結構

1，特點

1，是數據的邏輯結構在計算機存儲器中的映象（或表示）
2，存儲結構是通過計算機程序來實現，因而是依賴於具體的計算機語言的

2，存儲結構分類

1，順序存儲（Sequential Storage）：將數據結構中各元素按照其邏輯順序存放於存儲器一片連續的存儲空間中。
2，鏈式存儲（Linkend Storage）：將數據結構中各元素分佈到存儲器的不通電，用記錄下一個結點位置的方式建立他們之間的聯繫，由此得到的存儲結構為鏈式存儲結果。
3，索引存儲（Indexed Storage）：在存儲數據的同時，建立一個附加的索引表，即索引存儲結構=數據文件+索引表。

常用的數據結構

1，列表

　　列表（其他語言稱為數組，但是數組和Python的列表還是有區別的）是一種基本數據類型。

　　列表，在Python中稱為list，使用中括號包含，其中內部元素使用逗號分隔，內部元素可以是任何類型包含空。

1.1 數組和列表不同點

1，數組元素類型要相同，而Python列表不需要
2，數組長度固定，而Python列表可以增加

　　Python列表操作方法請參考此博客：https://www.cnblogs.com/wj-1314/p/8433116.html

2，元組

　　元組，Python中類為tuple。使用小括號包含，內部元素使用逗號分隔，可為任意值。與列表不同之處為，其內部元素不可修改，而且不能做刪除，更新操作。

　　注意：當元組中元素只有一個時，結尾要加逗號，若不加逗號，Python解釋器都將解釋成元素本身的類型，而非元組類型。

　　舉個例子：

>>> a = (1,2,3)  >>> b = ('1',[2,3])  >>> c = ('1','2',(3,4))  >>> d = ()  >>> e = (1,)

2.1 元組的操作

　　通過下標操作

通過小標來獲取元素值，使用方法同列表
切片的處理，使用方法同列表
不可通過下標做刪除和更新操作

　　如下，做出更改和刪除會報異常：

>>> c[0] = 1  Traceback (most recent call last):    File "<stdin>", line 1, in <module>  TypeError: 'tuple' object does not support item assignment    >>> del c[0]  Traceback (most recent call last):    File "<stdin>", line 1, in <module>  TypeError: 'tuple' object doesn't support item deletion

2.2 運算符及內建函數操作

　　元組本身是不可變，但是可以通過 + 來構成新的元組。

>>> a  (1, 2, 3)  >>> b  ('1', [2, 3])  >>> a + b  (1, 2, 3, '1', [2, 3])

　　可以通過使用內建函數 len 獲取元組長度，可以使用 * 元素來實現元素的重複

>>> a = (1,2,3)  >>> len(a)  3  >>> a*3  (1, 2, 3, 1, 2, 3, 1, 2, 3)

　　元組也支持 in 和 not in 成員運算符。

3，集合

　　集合用於包含一組無序的對象，與列表和元組不同，集合是無序的，也無法通過數字進行索引。此外，集合中的元素不能重複。set和dict一樣，只是沒有 value，相當於 dict 的 key 集合，由於 dict 的 key 是不重複的，且 key 是不可變對象，因此 set 有如下特性：

1，不重複，（互異性），也就是說集合是天生去重的
2，元素為不可變對象，（確定性，元素必須可 hash）
3，集合的元素沒有先後之分，（無序性）

　　Python的集合與數學中的集合一樣，也有交集，並集和合集。

　　舉例如下：

>>> s1 = {1,2,3,4,5}  >>> s2 = {1,2,3}  >>> s3 = {4,5}  >>> s1&s2   # 交集  {1, 2, 3}  >>> s1|s2   # 並集  {1, 2, 3, 4, 5}  >>> s1 - s2  # 差差集  {4, 5}  >>> s3.issubset(s1)   # s3 是否為s1 的子集  True  >>> s1.issuperset(s2)  # s1 是否為 s2 的超集  True

　　更多集合相關的操作參考博客：https://www.cnblogs.com/wj-1314/p/8423273.html

4，棧

　　棧（Stack）是一個數據集合，可以理解為只能在一段進行插入或刪除操作的列表。

　　棧的特點：後進先出 LIFO（Last-in， First-out）

　　棧的概念有：棧頂，棧底

　　棧的基本操作：

進棧（壓棧）：push
出棧：pop
取棧頂：gettop

　　對棧的理解，就像是一摞書，只能從上面放和取。

4.1 棧的實現

　　使用一般列表結構即可實現棧：

進棧：li.append
出棧：li.pop
取棧頂：li[-1]

　　那現在我們寫一個類實現它：

class Stack:        def __init__(self):          self.stack = []        def push(self, element):          self.stack.append(element)        def pop(self):          # 移除列表中的一個元素（默認最後一個），並返回該元素的值          return self.stack.pop()        def get_top(self):          if len(self.stack) > 0:              return self.stack[-1]          else:              return None    stack = Stack()  stack.push(1)  stack.push(2)  print(stack.pop())   # 2

4.2 棧的應用——括號匹配問題

　　我們可以通過棧來解決括號匹配的問題，就是解決IDE實現括號未匹配成功報錯的問題。

　　代碼：

class Stack:        def __init__(self):          self.stack = []        def push(self,element):          return self.stack.append(element)        def pop(self):          return self.stack.pop()        def get_top(self):          if len(self.stack) > 0:              return self.stack[-1]          else:              return None        def is_empty(self):          return len(self.stack) == 0    def brace_match(s):      match = {'}': '{', ']': '[', ')': '('}      stack = Stack()      for ch in s:          if ch in {'(', '[', '{'}:              stack.push(ch)          else:              if stack.is_empty():                  return False              elif stack.get_top() == match[ch]:                  stack.pop()              else:                  return False        if stack.is_empty():          return True      else:          return False    print(brace_match('{[{()}]}'))

5，隊列

　　隊列（Queue）是一個數據集合，僅允許在列表的一端進行插入，另一端進行刪除。進行插入的一端稱為隊尾（rear），插入動作稱為進隊或者入隊。進行刪除的一端稱為對頭（front），刪除動作稱為出隊。

　　隊列的性質：先進先出（First-in , First-out）

　　隊列可以並發的派多個線程，對排列的線程處理，並切每個需要處理線程只需要將請求的數據放入隊列容器的內存中，線程不需要等待，當排列完畢處理完數據後，線程在準時來取數據即可，請求數據的線程只與這個隊列容器存在關係，處理數據的線程down掉不會影響到請求數據的線程，隊列會派給其他線程處理這份數據，它實現了解耦，提高效率。隊列內會有一個順序的容器，列表與這個容器是有區別的，列表中數據雖然是排列的，但數據被取走後還會保留，而隊列中這些容器的數據被取後將不會保留。當必須在多個線程之間安全的交換信息時，隊列在線程編程中特別有用。

5.1 隊列的實現

　　隊列能否用列表簡單實現？為什麼？

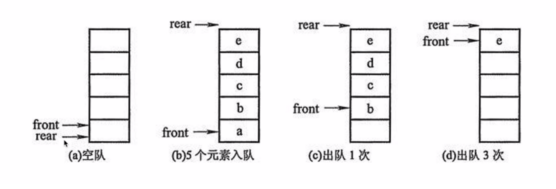
環形隊列的實現方式

　　環形隊列：當隊尾指針 front == MaxSize + 1 時，再前進一個位置就自動到0。

隊首指針前進1： front = (front + 1) % MaxSize
隊尾指針前進1： rear = (rear + 1) % MaxSize
隊空條件： front == rear
隊滿條件： (rear + 1) % MaxSize == front

class Queue:        def __init__(self, size):          self.queue = [0 for _ in range(size)]          self.size = size          self.rear = 0  # 隊尾指針是進隊的          self.front = 0  # 對首指針是出隊的        def push(self, element):          if not self.is_filled():              rear = (self.rear + 1) % self.size              self.queue[self.rear] = element          else:              raise IndexError("Queue is filled")        def pop(self):          if not self.is_empty():              self.front = (self.front + 1) % self.size              return self.queue[self.front]          else:              raise IndexError("Queue is empty")        # 判斷隊空      def is_empty(self):          return self.rear == self.front        # 判斷隊滿      def is_filled(self):          return (self.rear + 1) % self.size == self.front    q = Queue(5)  for i in range(4):      q.push(i)    print(q.pop())

from collections import deque    q = deque()  q.append(1)  # 隊尾進隊  print(q.popleft())  # 對首出隊    # 用於雙向隊列  q.appendleft(1)  # 隊首進隊  print(q.pop())   #隊尾出隊

　　雙向隊列的完整用法：

# _*_coding:utf-8_*_    # 創建雙向隊列  from collections import deque    d = deque()    # append（往右邊添加一個元素）  d.append(1)  d.append(2)  print(d)  # deque([1, 2])    # appendleft（往左邊添加一個元素）  d.appendleft(11)  d.appendleft(22)  print(d)  # deque([22, 11, 1, 2])    # clear清空隊列  d.clear()  print(d)  # deque([])    # 淺copy copy  d.append(1)  new_d = d.copy()  print(new_d)  # deque([1])    #  count(返回指定元素的出現次數)  d.append(1)  d.append(1)  print(d)  # deque([1, 1, 1])  print(d.count(1))  # 3    # extend(從隊列右邊擴展一個列表的元素)  d.append(2)  d.extend([3, 4, 5])  print(d)  # deque([1, 1, 1, 2, 3, 4, 5])    # extendleft(從隊列左邊擴展一個列表的元素)  d.extendleft([3, 4, 5])  print(d)  # deque([5, 4, 3, 1, 1, 1, 2, 3, 4, 5])    #  index（查找某個元素的索引位置）  d.clear()  d.extend(['a', 'b', 'c', 'd', 'e'])  print(d)  print(d.index('e'))  print(d.index('c', 0, 3))  # 指定查找區間  '''  deque(['a', 'b', 'c', 'd', 'e'])  4  2  '''    #  insert（在指定位置插入元素）  d.insert(2, 'z')  print(d)  # deque(['a', 'b', 'z', 'c', 'd', 'e'])    # pop（獲取最右邊一個元素，並在隊列中刪除）  x = d.pop()  print(x)  print(d)  '''  e  deque(['a', 'b', 'z', 'c', 'd'])  '''    # popleft（獲取最左邊一個元素，並在隊列中刪除）  print(d)  x = d.popleft()  print(x)  print(d)  '''  deque(['a', 'b', 'z', 'c', 'd'])  a  deque(['b', 'z', 'c', 'd'])  '''    # remove（刪除指定元素）  print(d)  d.remove('c')  print(d)  '''  deque(['b', 'z', 'c', 'd'])  deque(['b', 'z', 'd'])  '''    # reverse（隊列反轉）  print(d)  d.reverse()  print(d)  '''  deque(['b', 'z', 'd'])  deque(['d', 'z', 'b'])  '''    # rotate（把右邊元素放到左邊）  d.extend(['a', 'b', 'c', 'd', 'e'])  print(d)  d.rotate(2)  # 指定次數，默認1次  print(d)  '''  deque(['d', 'z', 'b', 'a', 'b', 'c', 'd', 'e'])  deque(['d', 'e', 'd', 'z', 'b', 'a', 'b', 'c'])  '''

Python四種類型的隊列

　　Queue：FIFO 即 first in first out 先進先出

　　LifoQueue：LIFO 即 last in first out 後進先出

　　PriorityQueue：優先隊列，級別越低，越優先

　　deque：雙邊隊列

導入三種隊列，包

from queue import Queue,LifoQueue,PriorityQueue

Queue：先進先出隊列

#基本FIFO隊列  先進先出 FIFO即First in First Out,先進先出  #maxsize設置隊列中，數據上限，小於或等於0則不限制，容器中大於這個數則阻塞，直到隊列中的數據被消掉  q = Queue(maxsize=0)    #寫入隊列數據  q.put(0)  q.put(1)  q.put(2)    #輸出當前隊列所有數據  print(q.queue)  #刪除隊列數據，並返回該數據  q.get()  #輸也所有隊列數據  print(q.queue)    # 輸出:  # deque([0, 1, 2])  # deque([1, 2])

LifoQueue：後進先出隊列：

#LIFO即Last in First Out,後進先出。與棧的類似，使用也很簡單,maxsize用法同上  lq = LifoQueue(maxsize=0)    #隊列寫入數據  lq.put(0)  lq.put(1)  lq.put(2)    #輸出隊列所有數據  print(lq.queue)  #刪除隊尾數據，並返回該數據  lq.get()  #輸出隊列所有數據  print(lq.queue)    #輸出:  # [0, 1, 2]  # [0, 1]

優先隊列

# 存儲數據時可設置優先級的隊列  # 優先級設置數越小等級越高  pq = PriorityQueue(maxsize=0)    #寫入隊列，設置優先級  pq.put((9,'a'))  pq.put((7,'c'))  pq.put((1,'d'))    #輸出隊例全部數據  print(pq.queue)    #取隊例數據，可以看到，是按優先級取的。  pq.get()  pq.get()  print(pq.queue)    #輸出：  [(9, 'a')]

雙邊隊列

#雙邊隊列  dq = deque(['a','b'])    #增加數據到隊尾  dq.append('c')  #增加數據到隊左  dq.appendleft('d')    #輸出隊列所有數據  print(dq)  #移除隊尾，並返回  print(dq.pop())  #移除隊左，並返回  print(dq.popleft())  #輸出:  deque(['d', 'a', 'b', 'c'])  c  d

6，鏈表

　　當我們存儲一大波數據時，我們很多時候是使用數組，但是當我們執行插入操作的時候就是非常麻煩，比如，有一堆數據1,2,3,5,6,7 我們要在3和5之間插入4，如果用數組，我們會怎麼辦？當然是將5之後的數據往後退一位，然後再插入4，這樣非常麻煩，但是如果用鏈表，就直接在3和5之間插入4即可。

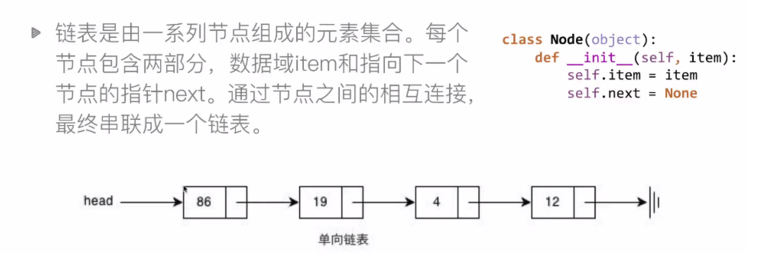
　　所以鏈表的節點結構如下：

　　data為自定義的數據，next為下一個節點的地址。head保存首位節點的地址。

　　首先可以看一個小鏈表，定義鏈表：

class Node:      def __init__(self, item):          self.item = item          self.next = None    a = Node(1)  b = Node(2)  c = Node(3)  # 通過next 將 a,b,c聯繫起來  a.next = b  b.next = c  # 打印a的下一個的下一個結果是什麼  print(a.next.next.item) # 3

　　當然，我們不可能這樣next來調用鏈表，使用循環等，下面繼續學習。

　　鏈表永遠有一個頭結點，head

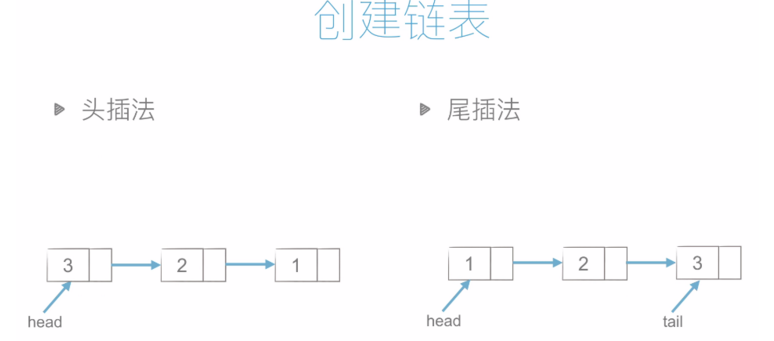
　　頭插法和尾插法的代碼如下：

class Node:      def __init__(self, item):          self.item = item          self.next = None    # 頭插法  # 這裡我們使用 li 進行循環插入  def create_linklist_head(li):      head = Node(li[0])      for element in li[1:]:          node = Node(element)          node.next = head  # 將頭結點 給剛插入的節點          head = node       # 然後將插入的節點設置為頭結點      return head    # 尾插法  def create_linklist_tail(li):      head = Node(li[0])      tail = head      for element in li[1:]:          node = Node(element)          tail.next = node          tail = node      return head    def print_linklist(lk):      while lk:          print(lk.item, end=',')          lk = lk.next      print('*********')    lk = create_linklist_head([1, 2, 3, 4])  # print(lk.item)  # 4  print_linklist(lk)  # 4,3,2,1,*********    lk = create_linklist_tail([1, 2, 3, 4, 5])  print_linklist(lk)  # 1,2,3,4,5,

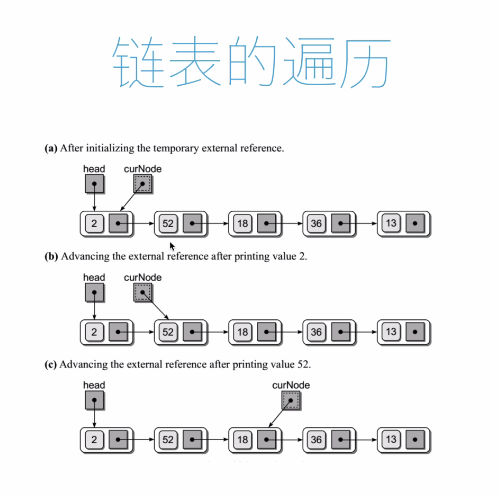
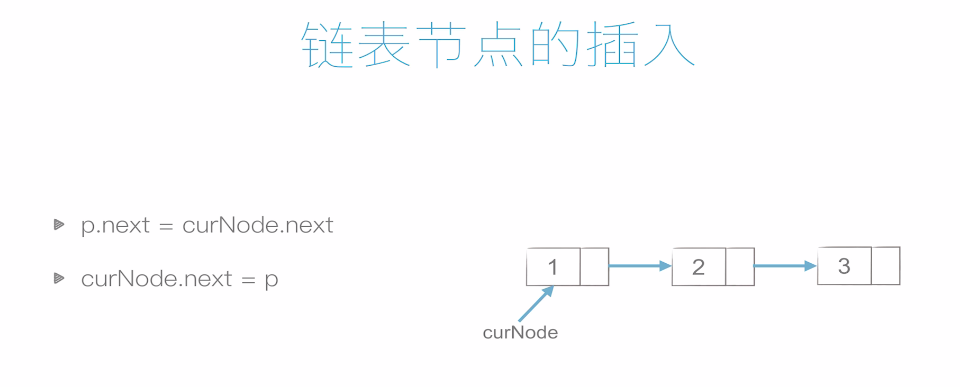
　　插入如下，非常簡單，所以時間複雜度也低。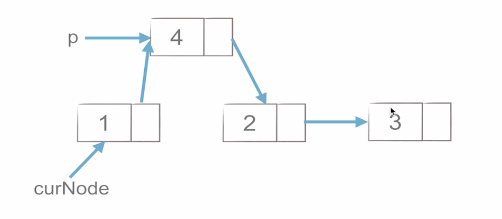

6.1 關於鏈表的方法

　　1，判斷是否為空：isEmpty()

def isEmpty(self):      return (self.length == 0)

　　2，增加一個節點（在鏈表尾添加）：append()

def append(self, dataOrNode):      item = None      if isinstance(dataOrNode, Node):          item = dataOrNode      else:          item = Node(dataOrNode)        if not self.head:          self.head = item          self.length += 1      else:          node = self.head          while node._next:              node = node._next          node._next = item          self.length += 1

　　3，刪除一個節點：delete()

# 刪除一個節點之後，記得把鏈表長度減一  def delete(self, index):      if self.isEmpty():          print("this chain table is empty")          return        if index < 0 or index >= self.length:          print('Error: out of index')          return        # 要注意刪除第一個節點的情況，如果有空的頭節點就不用這樣      if index == 0:          self.head = self.head._next          self.length -= 1          return        # prev 為保存前導節點      # node 為保存當前節點      # 當j 與index 相等時就相當於找到要刪除的節點      j = 0      node = self.head      prev = self.head      while node._next and j < index:          prev = node          node = node._next          j += 1        if j == index:          prev._next = node._next          self.length -= 1

　　4，修改一個節點：update()

def update(self, index, data):      if self.isEmpty() or index < 0 or index >= self.length:          print 'error: out of index'          return      j = 0      node = self.head      while node._next and j < index:          node = node._next          j += 1        if j == index:          node.data = data

　　5，查找一個節點：getItem()

def getItem(self, index):      if self.isEmpty() or index < 0 or index >= self.length:          print "error: out of index"          return      j = 0      node = self.head      while node._next and j < index:          node = node._next          j += 1        return node.data

　　6，查找一個節點的索引：getIndex()

def getIndex(self, data):      j = 0      if self.isEmpty():          print "this chain table is empty"          return      node = self.head      while node:          if node.data == data:              return j          node = node._next          j += 1        if j == self.length:          print "%s not found" % str(data)          return

　　7，插入一個節點：insert()

def insert(self, index, dataOrNode):      if self.isEmpty():          print "this chain tabale is empty"          return        if index < 0 or index >= self.length:          print "error: out of index"          return        item = None      if isinstance(dataOrNode, Node):          item = dataOrNode      else:          item = Node(dataOrNode)        if index == 0:          item._next = self.head          self.head = item          self.length += 1          return        j = 0      node = self.head      prev = self.head      while node._next and j < index:          prev = node          node = node._next          j += 1        if j == index:          item._next = node          prev._next = item          self.length += 1

　　8，清空鏈表：clear()

def clear(self):      self.head = None      self.length = 0

6.2 雙鏈表

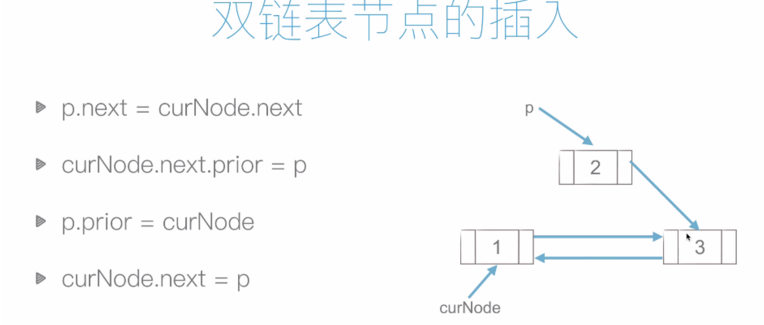
6.3 鏈表複雜度分析

　　順序表（列表/數組）與鏈表

按照元素值查找
按下標查找
在某元素後插入
刪除某元素

　鏈表與順序表

鏈表在插入和刪除的操作上明顯快於順序表
鏈表的內存可以更加靈活地分配（可以試利用鏈表重新實現棧和隊列）
鏈表這種鏈式存儲的數據結構對樹和圖的結構有很大的啟發性

7，哈希表（Hash table）

　　眾所周知，HashMap是一個用於存儲 Key-Value鍵值對的集合，每一個鍵值對也叫Entry，這些鍵值對（Entry）分散存儲在一個數組當中，這個數組就是HashMap的主幹。

　　使用哈希表可以進行非常快速的查找操作，查找時間為常數，同時不需要元素排列有序；Python的內建數據類型：字典就是用哈希表實現的。

　　Python中的這些東西都是哈希原理：字典(dictionary)、集合(set)、計數器(counter)、默認字典Defaut dict)、有序字典(Order dict).

　　哈希表示一個高效的查找的數據結構，哈希表一個通過哈希函數來計算數據存儲位置的數據結構，通常支持如下操作：

insert(key, value)：插入鍵值對（key, value）
get(key)：如果存在鍵為key的鍵值對則返回其value，否則返回空值
delete(key)：刪除鍵為key的鍵值對

直接尋址表

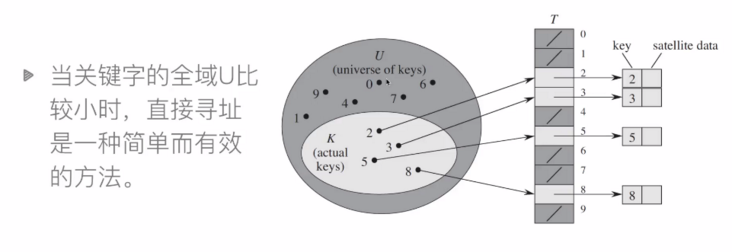
直接尋址技術缺點：

當域U很大時，需要消耗大量內存，很不實際
如果域U很大而實際出現的key很少，則大量空間被浪費
無法處理關鍵字不是數字的情況

哈希

　　直接尋址表：key為k的元素放到k位置上

　　改進直接尋址表：哈希（Hashing）

構建大小為m的尋址表T
key為k的元素放到 h(k)位置上
h(k) 是一個函數，其將域U映射到表 T[0, 1, … , m-1]

哈希表

　　哈希表（Hash Table，又稱為散列表），是一種線性表的存儲結構。哈希表由一個直接尋址表和一個哈希函數組成。哈希函數h(k)將元素關鍵字 k 作為自變量，返回元素的存儲下標。

　　假設有一個長度為7的哈希表，哈希函數 h(k)=k%7.元素集合 {14, 22, 3, 5}的存儲方式如下圖：

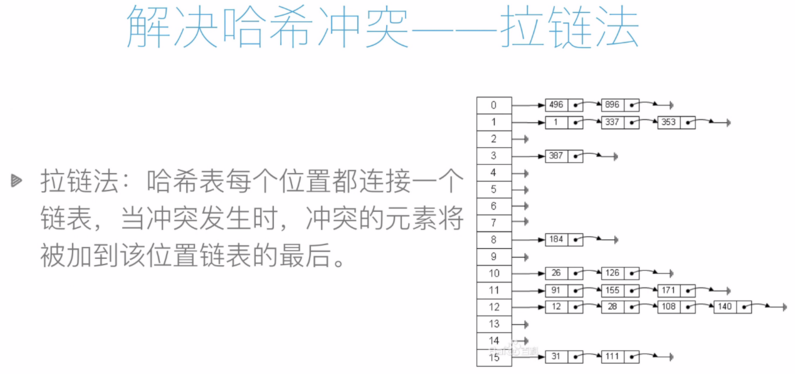
　　代碼如下：

class LinkList:      class Node:          def __init__(self, item=None):              self.item = item              self.next = None        class LinkListIterator:          def __init__(self, node):              self.node = node          def __next__(self):              if self.node:                  cur_node = self.node                  self.node = cur_node.next                  return cur_node.item              else:                  raise StopIteration          def __iter__(self):              return self        def __init__(self, iterable=None):          self.head = None          self.tail = None          if iterable:              self.extend(iterable)        def append(self, obj):          s = LinkList.Node(obj)          if not self.head:              self.head = s              self.tail = s          else:              self.tail.next = s              self.tail = s        def extend(self, iterable):          for obj in iterable:              self.append(obj)        def find(self, obj):          for n in self:              if n == obj:                  return True          else:              return False        def __iter__(self):          return self.LinkListIterator(self.head)        def __repr__(self):          return "<<" + ",".join(map(str, self)) + ">>"      # 類似於集合的結構  class HashTable:      def __init__(self, size=101):          self.size = size          self.T = [LinkList() for i in range(self.size)]        def h(self, k):          return k % self.size        def insert(self, k):          i = self.h(k)          if self.find(k):              print('Duplicated Insert')          else:              self.T[i].append(k)        def find(self, k):          i = self.h(k)          return self.T[i].find(k)

7.1 哈希表的應用

　　1，集合與字典

　　字典與集合都是通過哈希表來實現的。比如：

dic_res = {'name':'james', 'age':32, 'gender': 'Man'}

　　使用哈希表存儲字典，通過哈希表將字典的鍵映射為下標，假設 h(‘name’)=3，h(‘age’)=4，則哈希表存儲為：

[None, 32, None, 'james', 'Man']

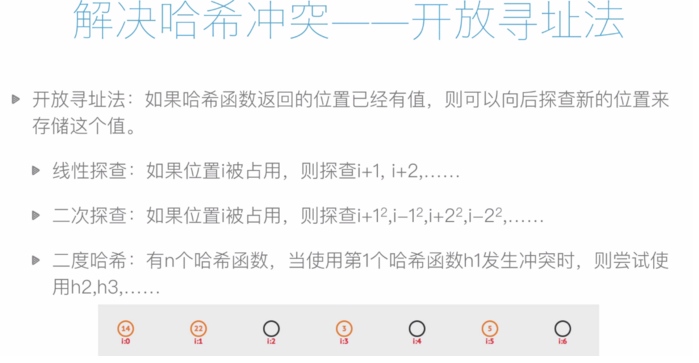
　　如果發生哈希衝突，則通過拉鏈法或開發尋址法解決。

　　2，md5算法

　　MD5（Message-Digest Algorithm 5）曾經是密碼學中常用的哈希函數，可以把任意長度的數據映射為128位的哈希值，其曾經包含如下特徵：

1，同樣的消息，其MD5值必定相同；
2，可以快速計算出任意給定消息的MD5值；
3，除非暴力的枚舉所有可能的消息，否則不可能從哈希值反推出消息本身；
4，兩天消息之間即使只有微小的差別，其對應的MD5值也應該是完全不同，完全不相關的；
5，不能再有意義的時間內人工的構造兩個不同的消息，使其具有相同的MD5值

　　3，md5

　　應用舉例：文件的哈希值

　　算出文件的哈希值，若兩個文件的哈希值相同，則可認為這兩個文件時相同的，因此：

1，用戶可以利用它來驗證下載的文件是否完整
2，雲存儲服務商可以利用它來判斷用戶要上次的文件是否已經存在於服務器上，從而實現秒傳的功能，同時避免存儲過多相同的文件副本。

　　 4，SHA2算法

　　歷史上MD5和SHA-1曾經是使用最為廣泛的 cryptographic hash function，但是隨着密碼學的發展，這兩個哈希函數的安全性相繼受到了各種挑戰。

　　因此現在安全性較重要的場合推薦使用 SHA-A等新的更安全的哈希函數。

　　SHA-2包含了一系列的哈希函數：SHA-224， SHA-256， SHA-384，SHA-512，SHA-512/224，SHA-512/256，其對應的哈希值長度分別為 224， 256， 384 or 512位。

　　SHA-2 具有和 MD5 類似的性質。

　　5，SHA2算法應用舉例

　　例如在比特幣系統中，所有參與者需要共同解決如下問題：對於一個給定的字符串U，給定的目標哈希值H，需要計算一個字符串V，使得 U+ V的哈希值與H的差小於一個給定值D。此時，只能通過暴力枚舉V來進行猜測。首先計算出結果的人可獲得一定獎金。而某人首先計算成功的概率與其擁有的計算量成正比，所以其獲得的獎金的期望值與其擁有的計算量成正比。

棧和隊列的應用——迷宮問題

　　給出一個二維列表，表示迷宮（0表示通道，1表示圍牆）。給出算法，求一條走出迷宮的路徑。

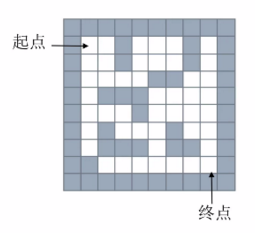
　　將其轉化為數組如下：

　　那有兩種思路，一種是使用棧（深度優先搜索）來存儲當前路徑，也可以稱為回溯法。但是深度優先有一個缺點，就是雖然能找到路徑，但是不能保證是最短路徑，其優點就是簡單，容易理解。

另一種方法就是隊列，

1，棧——深度優先搜索

　　回溯法

　　思路：從一個節點開始，任意找下一個能走的點，當炸不到能走的點時，退回上一個點尋找是否有其他方向的點。

　　使用棧存儲當前路徑

　　如下圖所示：

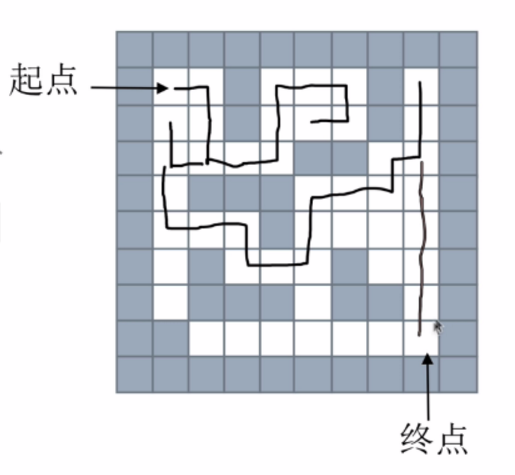
　　代碼如下：

# _*_coding:utf-8_*_    maze = [      [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],      [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],      [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],      [1, 0, 0, 0, 0, 1, 1, 0, 0, 1],      [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],      [1, 0, 0, 0, 1, 0, 0, 0, 0, 1],      [1, 0, 1, 0, 0, 0, 1, 0, 0, 1],      [1, 0, 1, 1, 1, 0, 1, 1, 0, 1],      [1, 1, 0, 0, 0, 0, 0, 0, 0, 1],      [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]  ]    # 這裡我們封裝一個列表,用來表示走迷宮的四個方向  dirs = [      lambda x, y: (x + 1, y),  # 表示向上走      lambda x, y: (x - 1, y),  # 表示向下走      lambda x, y: (x, y - 1),  # 表示向左走      lambda x, y: (x, y + 1),  # 表示向右走  ]      def maze_path(x1, y1, x2, y2):      stack = []      stack.append((x1, y1))      while (len(stack) > 0):          curNode = stack[-1]  # 當前節點是 stack最後一個位置          if curNode[0] == x2 and curNode[1] == y2:              return True  # 如果有路則返回TRUE，沒有路則返回FALSE          # x,y當前坐標，四個方向上下左右分別是：x-1,y  x+1,y  x, y-1  x,y+1          for dir in dirs:              nextNode = dir(curNode[0], curNode[1])              # 如果下一個節點能走              if maze[nextNode[0]][nextNode[1]] == 0:                  stack.append(nextNode)                  maze[nextNode[0]][nextNode[1]] = 2  # 2表示已經走過了                  break          else:  # 如果一個都找不到，就需要回退了              maze[nextNode[0]][nextNode[1]] = 2              stack.pop()  # 棧頂出棧，也就是回退        else:          print("沒有路")          return False      maze_path(1, 1, 8, 8)

2，隊列——廣度優先搜索

　　思路：從下一個節點開始，尋找所有接下來能繼續走的點，繼續不斷尋找，直到找到出口。

　　使用隊列存儲當前正在考慮的節點

　　思路圖如下：

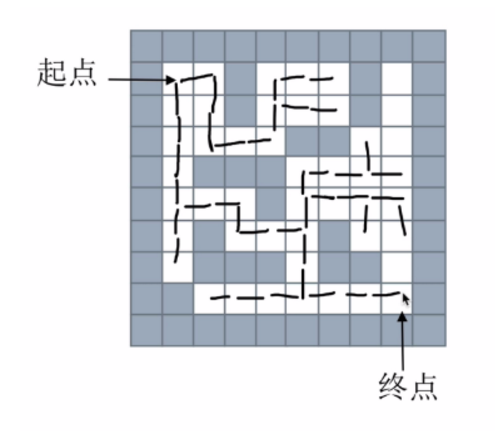
或者這樣：

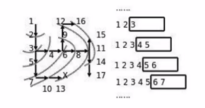
可以通過如下方式理解：

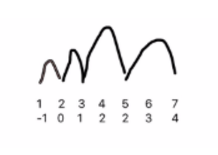
　　代碼如下：

# _*_coding:utf-8_*_  from collections import deque    maze = [      [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],      [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],      [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],      [1, 0, 0, 0, 0, 1, 1, 0, 0, 1],      [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],      [1, 0, 0, 0, 1, 0, 0, 0, 0, 1],      [1, 0, 1, 0, 0, 0, 1, 0, 0, 1],      [1, 0, 1, 1, 1, 0, 1, 1, 0, 1],      [1, 1, 0, 0, 0, 0, 0, 0, 0, 1],      [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]  ]    dirs = [      lambda x, y: (x + 1, y),  # 表示向上走      lambda x, y: (x - 1, y),  # 表示向下走      lambda x, y: (x, y - 1),  # 表示向左走      lambda x, y: (x, y + 1),  # 表示向右走  ]    def print_r(path):      real_path = []  # 用來存儲真實的路徑      i = len(path) - 1  # 用i指向path的最後一個下標      while i >= 0:          real_path.append(path[i][0:2])          i = path[i][2]      real_path.reverse()    # 起點坐標（x1, y1)  終點坐標（x2, y2）  def maze_path_queue(x1, y1, x2, y2):      queue = deque()      path = []      # -1  為當前path的路徑的下標      queue.append((x1, y1, -1))      while len(queue) > 0:  # 當隊列不空時循環          # append是從右邊加入的，popleft()從左邊出去          cur_Node = queue.popleft()          path.append(cur_Node)          if cur_Node[0] == x2 and cur_Node[1] == y2:              # 如果當前節點等於終點節點，則說明到達終點              print_r(path)              return True            # 隊列是找四個方向，每個能走就繼續          for dir in dirs:              # 下一個方向的節點坐標              next_node = dir(cur_Node[0], cur_Node[1])              if maze[next_node[0]][next_node[1]] == 0:                  queue.append((next_node[0], next_node[1], len(path) - 1))                  maze[next_node[0]][next_node[1]] = 2  # 標記為已走過      return False  # 如果隊列結束了，空了，還沒找到路徑，則為FALSE      maze_path_queue(1, 1, 8, 8)