機器學習項目實戰—-泰坦尼克號獲救預測(一)
- 2019 年 10 月 3 日
- 筆記
一、任務基礎
泰坦尼克號沉沒是歷史上最著名的沉船事故之一。1912年4月15日,在她的處女航中,泰坦尼克號在與冰山相撞後沉沒,在2224名乘客和機組人員中造成1502人死亡。這場聳人聽聞的悲劇震驚了國際社會,並為船舶制定了更好的安全規定。造成海難失事的原因之一是乘客和機組人員沒有足夠的救生艇。儘管倖存下沉有一些運氣因素,但有些人比其他人更容易生存,例如婦女,兒童和上流社會。在這個案例中我們將運用機器學習來預測哪些乘客可以倖免於悲劇。
數據集鏈接:https://pan.baidu.com/s/1bVnIM5JVZjib1znZIDn10g 。提取碼:1htm 。
讀取titanic_train數據集
import pandas # 讀取數據集 titanic = pandas.read_csv('titanic_train.csv') titanic.head(10)
查看數據集前10行
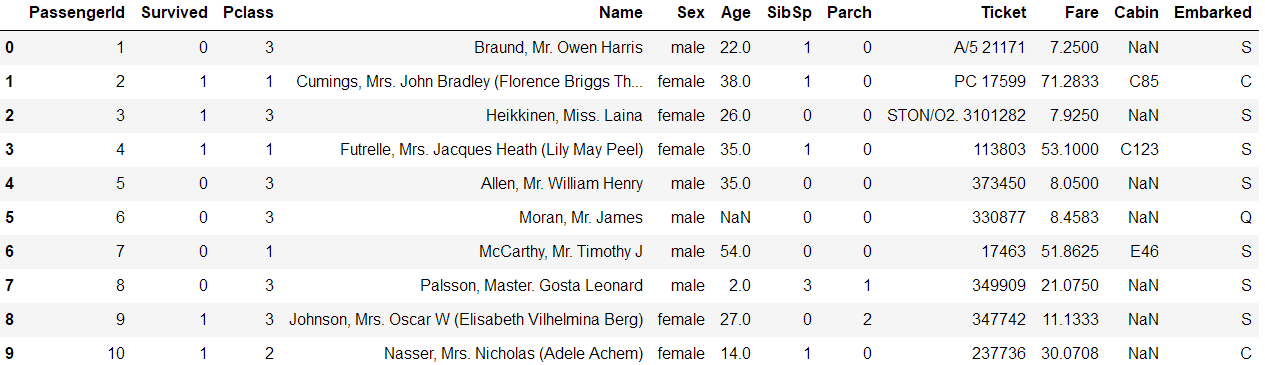
特徵名詞解釋
| 特徵名稱 | 特徵解釋 |
| PassengerId | 乘客id,對結果沒有影響 |
| Survived | 1表示存活,0表示未存活 |
| Pclass | 船艙等級,越有錢船艙等級越高,所以對結果有影響 |
| Name | 乘客名字,先暫時認為對結果沒有影響 |
| Sex | 性別,毫無疑問,女生優先,所以肯定對結果有影響 |
| Age | 年齡,不用說這列也有影響 |
| SibSp | 兄弟姐妹,對結果也有影響 |
| Parch | 父母和小孩,不用說也有影響 |
| Ticket | 票的編號,貌似沒啥影響 |
| Fare | 船票價格,和船艙等級一樣,不能忽略 |
| Cabin | 船艙號,應該也沒啥影響 |
| Embarked | 登船地點,不同地點登船可能身份不一樣 |
二、數據預處理
可以看到Age列有缺失值(NaN)。一般來說,數據發生缺失的話有兩種處理方法,一種填充缺失值,一種直接捨棄這個特徵。這裡一般來說Age對結果是有較大影響的,我們可以對缺失值進行填充,這裡可以填充平均值 。
# Age 缺失值填充 titanic['Age'] = titanic['Age'].fillna(titanic['Age'].median()) print(titanic.describe())
填充後查看數據集的描述
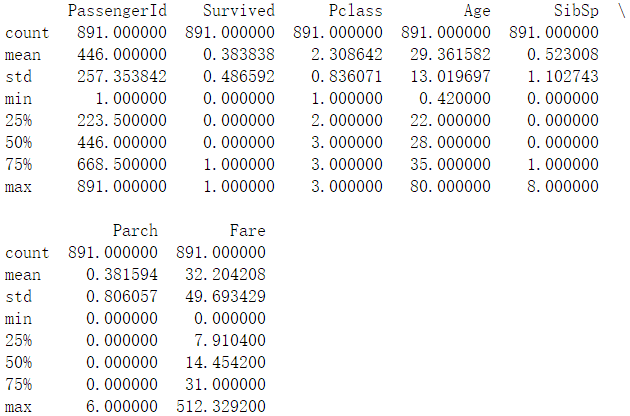
機器學習算法一般來說解決不了對字符的分類。因為我們是要對Survived這列‘’0‘’和”1″進行分類嘛。所以我們就要把”Sex”這一列的數據進行處理,把它映射為數值型。那我們就把”male”和“female”進行處理,分別用0和1替代。
# print(titanic['Sex'].unique()) # Replace all the occurences of male with the number 0. # 用數字0替換所有出現的男性。 titanic.loc[titanic["Sex"] == "male", "Sex"] = 0 titanic.loc[titanic["Sex"] == "female", "Sex"] = 1
同時,我們也把”Embarked”這一列數據進行同樣的處理
# print(titanic['Embarked'].unique()) # Embarked:上船港口,有三個取值,C/S/Q,是文字形式,不利於分析, # 故可能需要映射到數值的值,而且有2個缺失值 titanic['Embarked'] = titanic['Embarked'].fillna('S') # 缺失值填充為這一列的眾數'S' titanic.loc[titanic["Embarked"] == "S", "Embarked"] = 0 titanic.loc[titanic["Embarked"] == "C", "Embarked"] = 1 titanic.loc[titanic["Embarked"] == "Q", "Embarked"] = 2
三、分類任務
首先使用線性回歸算法來進行分類
# Import the linear regression(回歸) class # 注意不要導錯庫 from sklearn.linear_model import LinearRegression from sklearn.model_selection import KFold # The columns we'll use to predict the target predictors = ['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Embarked'] # Initialize our algorithm class alg = LinearRegression() # Generate cross validation folds for the titanic dataset. It return the row indices # corresponding(相應的) to train and test. # 為Titanic數據集生成交叉驗證摺疊。它返回與訓練和測試相對應的行索引。 # We set random_state to ensure we get the same splits every time we run this. # kf = KFold(titanic.shape[0], n_folds=3, random_state=1) 寫法錯誤已被棄用 # 樣本平均分成3份,3折交叉驗證 kf = KFold(n_splits=3,shuffle=False, random_state=1) # 注意這裡不是kf.split(titanic.shape[0]),會報如下錯誤: # Singleton array array(891) cannot be considered a valid collection. predictions = []
# 交叉驗證 劃分訓練集 驗證集 for train, test in kf.split(titanic): # The predictors we're using the train the algorithm. Note how we only take # the rows in the train folds # 注意我們只得到訓練集的rows train_predictors = titanic[predictors].iloc[train, :] # The target we're using to train the algorithm. train_target = titanic['Survived'].iloc[train] # Training the algorithm using the predictors and target alg.fit(train_predictors, train_target) # We can now make predictions on the test fold test_predictions = alg.predict(titanic[predictors].iloc[test, :]) predictions.append(test_predictions)
查看線性回歸準確率
import numpy as np # The predictions are in three separate numpy arrays. Concatenate them into one. # We concatenate them on asix 0, as they only have one axis. predictions = np.concatenate(predictions,axis=0) # Map predictions to outcomes (only possible outcomes are 1 and 0) predictions[predictions > .5] = 1 # 映射成分類結果 計算準確率 predictions[predictions <= .5] = 0 # 注意這一行與源代碼有出入 accuracy = sum(predictions==titanic['Survived'])/len(predictions) # 驗證集的準確率 print(accuracy)
得到的準確率為
0.7833894500561167
對於一個二分類問題來說,這個準確率似乎不太行,接下來用邏輯回歸算法試下
from sklearn.model_selection import cross_val_score from sklearn.linear_model import LogisticRegression alg = LogisticRegression(random_state=1) # Compute the accuracy score for all the cross validation folds, # (much simper than what we did before!) scores = cross_val_score(alg, titanic[predictors], titanic["Survived"], cv=3) # Take the mean of the scores (because we have one for each fold) print(scores.mean())
得到的準確率為,可以發現效果要好了一點。
0.8047138047138048
上面得到的結果都是對交叉驗證後的驗證集來進行分類,在實際結果中,應該使用測試數據集來進行分類。
讀取測試數據集並填充數據集,然後進行數值映射,與上面類似。
titanic_test = pandas.read_csv("test.csv") titanic_test["Age"] = titanic_test["Age"].fillna(titanic["Age"].median()) titanic_test["Fare"] = titanic_test["Fare"].fillna(titanic_test["Fare"].median()) titanic_test.loc[titanic_test["Sex"] == "male", "Sex"] = 0 titanic_test.loc[titanic_test["Sex"] == "female", "Sex"] = 1 titanic_test["Embarked"] = titanic_test["Embarked"].fillna("S") titanic_test.loc[titanic_test["Embarked"] == "S", "Embarked"] = 0 titanic_test.loc[titanic_test["Embarked"] == "C", "Embarked"] = 1 titanic_test.loc[titanic_test["Embarked"] == "Q", "Embarked"] = 2
通過上面發現,似乎線性回歸,邏輯回歸這類算法似乎不太行,那這次再用隨機森林算法來試下(一般來說隨機森林算法比線性回歸和邏輯回歸算法的效果好一點),注意隨機森林參數的變化。
from sklearn.model_selection import cross_val_score from sklearn.model_selection import KFold from sklearn.ensemble import RandomForestClassifier predictors = ["Pclass", "Sex", "Age", "SibSp", "Parch", "Fare", "Embarked"] # Initialize our algorithm with the default paramters # n_estimators is the number of trees we want to make # min_samples_split is the minimum number of rows we need to make a split # min_samples_leaf is the minimum number of samples we can have at the place where a # tree branch(分支) ends (the bottom points of the tree) alg = RandomForestClassifier(random_state=1, n_estimators=10, min_samples_split=2, min_samples_leaf=1) # Compute the accuracy score for all the cross validation folds. (much simpler than what we did before!) kf = KFold(n_splits=3, shuffle=False, random_state=1) scores = cross_val_score(alg, titanic[predictors], titanic["Survived"], cv=kf) # Take the mean of the scores (because we have one for each fold) print(scores.mean())
準確率為:
0.7856341189674523
發現準確率還是不太行。在機器學習中,調整參數也是非常重要的,一般通過參數的調整來對模型進行優化。這次調整隨機森林的參數。
alg = RandomForestClassifier(random_state=1, n_estimators=100, min_samples_split=4, min_samples_leaf=2) # Compute the accuracy score for all the cross validation folds. (much simpler than what we did before!) kf = KFold(n_splits=3, shuffle=False, random_state=1) scores = cross_val_score(alg, titanic[predictors], titanic["Survived"], cv=kf) # Take the mean of the scores (because we have one for each fold) print(scores.mean())
得到的準確率為:
0.8148148148148148
未完待續。。。
