2019.9.25 初級數據結構——樹狀數組

• 2019 年 10 月 8 日
• 筆記

一、樹狀數組基礎

學OI的同學都知道，位運算（對二進制的運算）比普通運算快很多。同時我們接觸到了狀態壓縮的思想（即將0-1的很多個狀態壓縮成十進制的一個數，每一個二進制位表示一個狀態）。由於在實際做題過程當中，由於數據範圍限制，我們必須採用更高效的存儲、查詢方法，於是樹狀數組應運而生。

首先我們檢查傳統的存儲狀態。對於數組的每一個下標i，其所存儲的有效信息只有一個a[i]（這是傳統數組）。而對於樹狀數組，我們每一位下標可以存儲lowbit(i)個有效信息。這個lowbit運算一會再說。所以儘管樹狀數組很難壓縮真正的存儲空間，但查詢的時候可以把n的複雜度壓縮成log（n）。這裡的查詢指區間查詢和單點修改。

為什麼有這樣的查詢效率？對於一個區間[1,x]，我們把它分成log(x)個小區間。設x=2ⁱ¹+2ⁱ²+……2^im（這不由得讓我們想起快速冪的分解方法），不妨設i1>i2>……>im，則我們可以把[1,x]分成以下小區間：

(1)長度為2ⁱ¹的小區間[1,2ⁱ¹]

(2)長度為2ⁱ²的小區間[2ⁱ¹+1,2ⁱ¹+2ⁱ²]

……

(log(n))長度為2^im的小區間[2^im-1+1,……+2^im]

比如[1,6]可以分成[1,4]和[5,6]

所以我們如果想修改這個區間[1,x]的和，我們只需要修改這log(n)個區間的的和即可。

先上個圖：

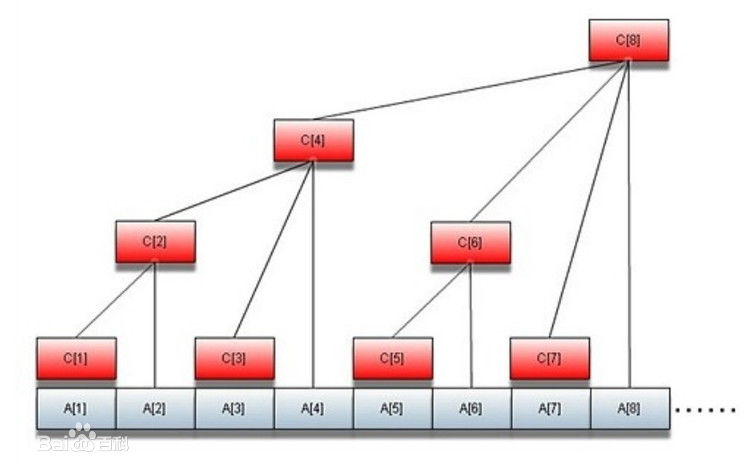
所以我們現在的問題在於，如果我們要查找a[idx]的前綴和，假設最開始idx是6：

則我們先加上最後一段小區間，令idx=6-2¹；

再加上第一段小區間，令idx=6-2¹-2²。

應當注意的是，我們每次多減去的那個2ⁱ，實際上那個i是idx的二進制最靠近個位的那一位1對應到的數的編號。

舉個例子：

10的二進制是1010，最靠近個位的一個1是在第二位，所以我們第一次減掉2²；

得到的新數是8，二進制是1000，最靠近個位的一個1是在第四位，所以我們減掉2⁴得到0。

我們減掉2^k這個過程，我們把它量化，記原來的數組是a，我們開的數組是c，則每次我們加上的區間就是c[idx]，然後idx往前移動到c[idx]存儲的區間的前一位，繼續這個步驟。

比如說，我們要計算a[1]到a[6]的和，我們讓idx=6，我們發現剛才我們拆分[1,6]的結果最後一個小區間是[5,6]，所以我們用c[6]記錄a[5]+a[6]，然後跳到c[4]，用c[4]記錄a[1]+a[2]+a[3]+a[4]，即可得到答案。c數組就是我們說的樹狀數組。

那到底這個[1,n]的小區間怎麼拆分？因為我們每次減掉的那個2ⁱ的i都是離個位最近的一個1所在的位置，所以我們只需要按照上述規則從後往前遍歷n的所有二進制位，就可以遍歷存儲這個數的所有小區間。

比如說我們從6(110)遍歷到4(100)（其中經過了[5,6]），然後遍歷到0，其中經過了[1,4]。

也就是說，我們只需要找到每次要減掉的2ⁱ即可。

重點來了！！！

我們定義每次減掉的數是lowbit(i)（其中i是進行減法操作之前的數），也就是說lowbit(i)=2^m，其中m是i的二進制最靠個位一個1的位置。定義了這個，我們實際上就是定義c[i]是以a[i]結尾長度為lowbit(i)的a數組內的區間，即c[i]=a[i-lowbit(i)+1]+a[i-lowbit(i)+2]+……+a[i]。這樣每次idx跳躍一個lowbit(idx)，就相當於恰好跳過了需要被加上的一段小區間，而加上這一段小區間的和只需要O(1)的複雜度。

怎麼算這個lowbit(i)？這就要用到科學家們的智慧。

lowbit(i)=x&(-x)。

為什麼這個數就能滿足我們的要求？

我們來補充一點二進制的知識：

我們在存儲一個數時，int類型是一個32位有符號整數，其中第一位是符號位，1表示負數，0表示正數。

 這裡利用的負數的存儲特性，負數是以補碼存儲的，對於整數運算 x&(-x)有

       ● 當x為0時，即 0 & 0，結果為0；

       ●當x為奇數時，最後一個比特位為1，取反加1沒有進位，故x和-x除最後一位外前面的位正好相反，按位與結果為0。結果為1。

       ●當x為偶數，且為2的m次方時，x的二進制表示中只有一位是1（從右往左的第m+1位），其右邊有m位0，故x取反加1後，從右到左第有m個0，第m+1位及

其左邊全是1。這樣，x& (-x) 得到的就是x。 

      ●當x為偶數，卻不為2的m次方的形式時，可以寫作x= y * (2^k)。其中，y的最低位為1。實際上就是把x用一個奇數左移k位來表示。這時，x的二進制表示最

右邊有k個0，從右往左第k+1位為1。當對x取反時，最右邊的k位0變成1，第k+1位變為0；再加1，最右邊的k位就又變成了0，第k+1位因為進位的關係變成了1。

左邊的位因為沒有進位，正好和x原來對應的位上的值相反。二者按位與，得到：第k+1位上為1，左邊右邊都為0。結果為2^k。

        總結一下：x&(-x)，當x為0時結果為0；x為奇數時，結果為1；x為偶數時，結果為x中2的最大次方的因子。

一定注意，lowbit(0)會陷入死循環。

 所以我們只需要利用這種運算，就可以在log(n)的複雜度內分割小區間，從而計算從a[1]到a[n]的和。

同樣我們考慮修改一個值a[idx]，因為c數組存儲a數組的值有重複，所以我們必須將所有包含a[idx]的c[i]都進行修改。所以，同剛才的步驟，我們只需要根據某種順序順次查找每個包含a[idx]的c[i]即可。

 這個順序非常容易想到：

剛才我們已經知道，我們用c[i]表示從i往前數lowbit(i)個a[i]的總和。根據樹狀數組的特殊結構，我們查找的步驟如下：

找到c[i]（肯定包含a[i]）—–>找到第一個包含c[i]的c[j]———>找到第一個包含c[j]的c[k]……

一定注意這個步驟，這是因為樹狀數組的本質是一棵樹，一個點只有一個父親，這個我們之後會說。

根據lowbit的定義，同時根據二進制的特性，有以下兩個特徵：

（1）lowbit每向左移一位，其表示的lowbit(i)（也就是對應的區間長度，見前文）就乘以2；

（2）根據上文，我們要找到的數實際上是比他大的第一個lowbit往前移動一位的數（比如說5（101），6（110），lowbit移動了一位）。

所以我們怎麼找這樣的數？？？

要解決這個問題，我們必須回到二進制的加法：

比如說6+2，在二進制里的表示是這樣的：

    1 1 0

+0 1 0

—1——-

1 0 0 0

大家很容易注意到，第二位的兩個1加起來之後進位到上一位一個1，因為上一位也有一個1，所以必須再進位；以此類推，它會一直進位直到進位到第一個數的lowbit前面的0上，把它變成1。

這難道不是我們剛才要的lowbit移動的方法？？我們已經把最後一個1進位到了前面。我們只需要找到第二個和它相加的那個數即可。

因為要進位最後一個1，同時我們需要使底下那個數最小，所以我們只需要找到一個數，它前面後面都是0，中間那個與第一個數最後一個1對上的那一位是1.不明白的參見上面的例子。

有沒有覺得上面這個很熟悉？？？？

綜上所述，我們得到：

（1）樹狀數組求前綴和：求1-i的和，每次加上c[i]，然後減去lowbit(i)。

（2）樹狀數組單點修改：修改a[i]時修改c[idx]，然後idx+=lowbit(idx)，最開始idx=i。

 二、樹狀數組的幾何認識

剛才我們已經了解了樹狀數組的基本操作，下面我們從樹本身的角度認識樹狀數組的性質和操作。

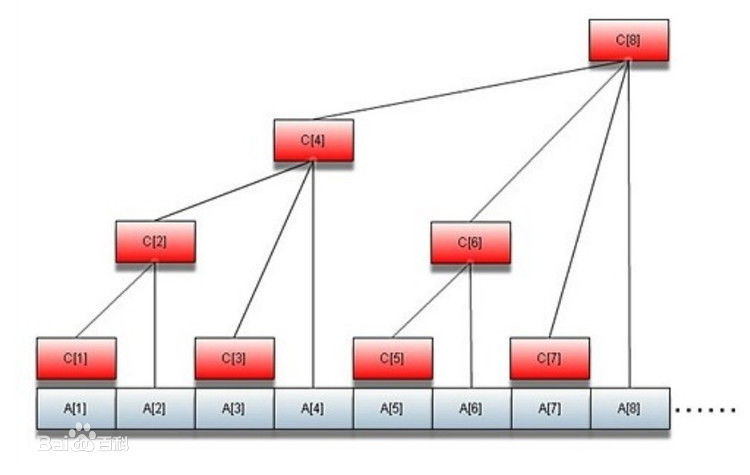
根據上面的圖我們可以知道，樹狀數組具有以下幾個性質：

（1）紅色節點和其父親之間的橫向距離是lowbit(i)，這是樹狀數組構建的基礎，所以我們每次修改一個a[i]的值其實是修改所有以c[i]為根的且包含a[i]的子樹的c[i]的值，也就是說從a[i]每次向上找到其父親，並修改a[i]每一級父親的值即可。

（2）查找一個點的前綴和時，相當於從這個點每次找到它的兒子覆蓋的區間，而每個點覆蓋的區間是從這個點到它最左邊的兒子，所以每次減去lowbit(i)即可。

高級用法待填坑。