二叉查找樹(查找、插入、刪除)——C語言
- 2019 年 10 月 3 日
- 筆記
二叉查找樹
二叉查找樹(BST:Binary Search Tree)是一種特殊的二叉樹,它改善了二叉樹節點查找的效率。二叉查找樹有以下性質:
二叉查找樹節點的定義:
1 typedef struct BSTreeNode 2 { 3 int data; 4 struct BSTreeNode *left;//左子樹 5 struct BSTreeNode *right;//右子樹 6 }BSTree;
跟普通二叉樹的節點定義相同
因為查找節點和插入節點都是在已經構建好二叉查找樹的前提下才能進行的,在刪除節點的時候才涉及到調整二叉樹的操作,所以這裡先以前序遍歷的順序直接輸入一個二叉查找樹,代碼如下

1 /* 創建二叉查找樹(數據以前序遍歷順序輸入)*/ 2 BSTree *Create_BSTreeNode(BSTree *nod) 3 { 4 int num; 5 6 scanf_s("%d", &num, 1); 7 if (num == 0) /* 假定輸入的數據都為正數,以0作為NULL的標誌 */ 8 { 9 return NULL; 10 } 11 else 12 { 13 if ((nod = (BSTree *)malloc(sizeof(BSTree))) == NULL) 14 { 15 printf("內存空間不足"); 16 exit(0); 17 } 18 nod->data = num; 19 nod->left = Create_BSTreeNode(nod->left); 20 nod->right = Create_BSTreeNode(nod->right); 21 22 return nod; 23 } 24 } 25 26 /* 前序遍歷二叉樹,並打印 */ 27 void PreOrder_Traverse(BSTree *nod, int level) 28 { 29 if (nod == NULL) 30 { 31 return ; 32 } 33 34 printf("data = %d level = %dn", nod->data, level); 35 PreOrder_Traverse(nod->left, level + 1); 36 PreOrder_Traverse(nod->right, level + 1); 37 }
View Code
1、查找節點(遞歸實現)
若根結點的關鍵字等於查找的關鍵字,查找成功,若小於根結點的關鍵字的值,遞歸查找左子樹,若大於根結點的關鍵字的值,遞歸查找右子樹,若子樹為空,則查找失敗,查找的操作較為簡單,實現代碼如下
1 /* 查找特定值 */ 2 void SearchData(int targ, BSTree *nod) 3 { 4 if (nod != NULL) 5 { 6 if (nod->data == targ) 7 { 8 printf("查找值存在,值為%dn", nod->data); 9 } 10 else if (nod->data > targ) 11 { 12 SearchData(targ, nod->left); //遞歸查找左子樹 13 } 14 else if (nod->data < targ) 15 { 16 SearchData(targ, nod->right); //遞歸查找右子樹 17 } 18 } 19 else if (nod == NULL) 20 { 21 printf("查找值不存在n"); 22 } 23 }
通過 BST 查找節點,理想情況下我們需要檢查的節點數可以減半。如下圖中的 BST 樹,包含了 15 個節點。從根節點開始執行查找算法,第一次比較決定我們是移向左子樹還是右子樹,對於任意一種情況,一旦執行這一步,我們需要訪問的節點數就減少了一半,從 15 降到了 7。同樣,下一步訪問的節點也減少了一半,從 7 降到了 3,以此類推,根據這一特點,查找算法的時間複雜度應該是 O(log2n)

(圖片來源:https://www.cnblogs.com/gaochundong/p/binary_search_tree.html)
對於 BST 查找算法來說,其十分依賴於樹中節點的拓撲結構,也就是節點間的布局關係,當 BST 樹中的節點以扇形結構散開時,對它的插入、刪除和查找操作最優的情況下可以達到亞線性的運行時間 O(log2n),
因為當在 BST 中查找一個節點時,每一步比較操作後都會將節點的數量減少一半。儘管如此,如果拓撲結構像下圖中的樣子時,運行時間就會退減到線性時間 O(n)。因為每一步比較操作後還是需要逐個比較其餘的節點,
也就是說,在這種情況下,在 BST 中查找節點與在數組(Array)中查找就基本類似了。
因此,BST 算法查找時間依賴於樹的拓撲結構。最佳情況是 O(log2n),而最壞情況是 O(n)

測試用例:
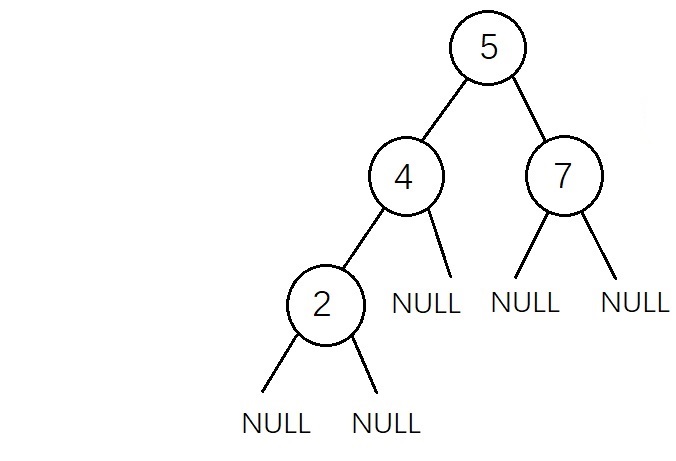
查找:以前序遍歷順序輸入一個二叉查找樹(0作為NULL標誌)
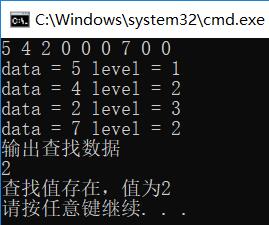
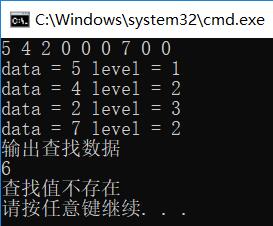
2、插入節點(遞歸實現)
新插入的結點一定是一個新添加的葉子結點,如下圖
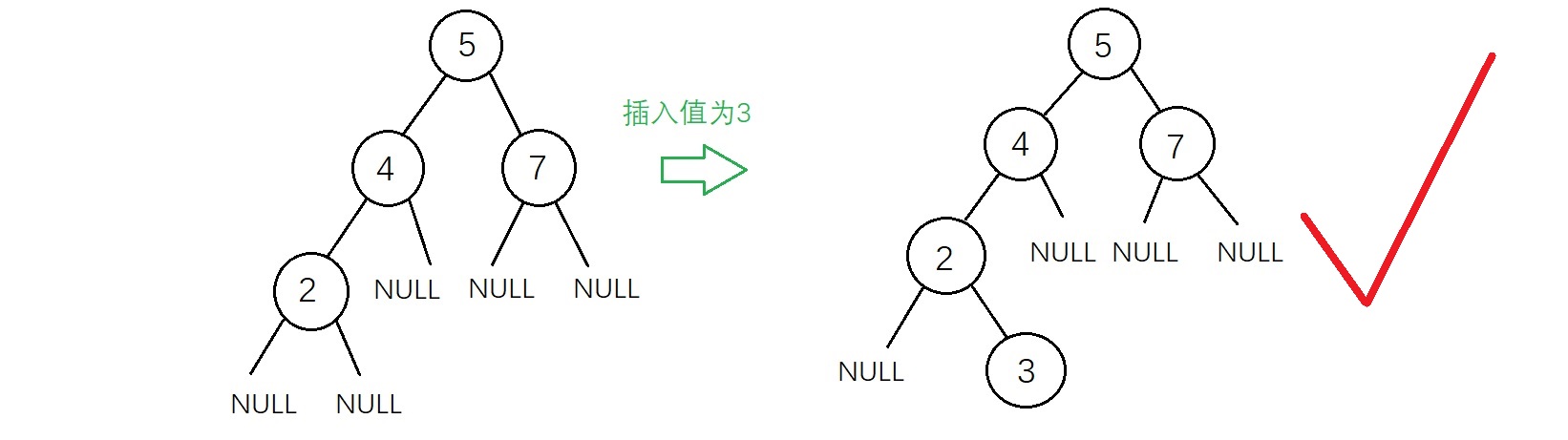
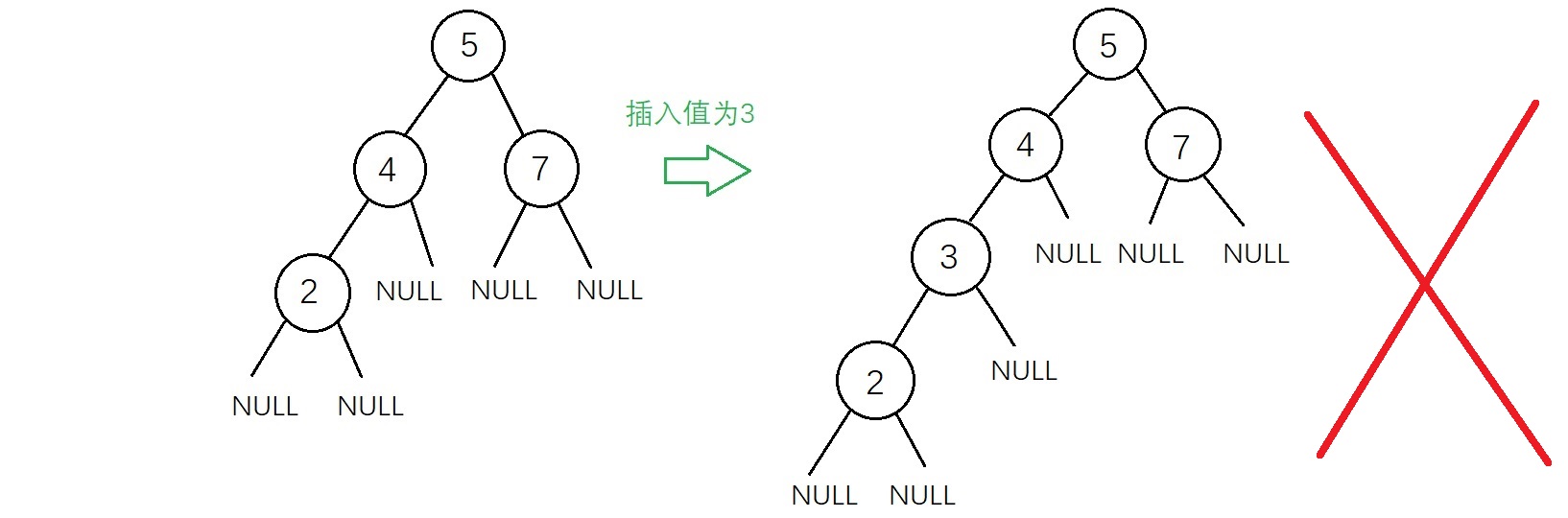
雖然上面兩種插入結果得到的二叉樹都符合二叉查找樹的性質,但是不滿足“新插入的結點一定是一個新添加的葉子結點”,因為有了這個特點插入的操作變得相對簡單,實現代碼如下
1 /* 添加新節點 */ 2 BSTree *AddNewNode(BSTree *cur, int NewData) 3 { 4 if (cur == NULL) 5 { 6 if ((cur = (BSTree *)malloc(sizeof(BSTree))) == NULL) //創建新節點 7 { 8 printf("內存不足"); 9 exit(0); 10 } 11 cur->data = NewData; 12 cur->left = NULL; 13 cur->right = NULL; 14 15 return cur; 16 } 17 if (NewData > cur->data) 18 { 19 cur->right = AddNewNode(cur->right, NewData); 20 } 21 else if (NewData < cur->data) 22 { 23 cur->left = AddNewNode(cur->left, NewData); 24 } 25 else if (NewData == cur->data) 26 { 27 printf("不允許插入重複值n"); 28 exit(0); 29 } 30 31 return cur; 32 }
測試用例:

插入:以前序遍歷順序輸入一個二叉查找樹

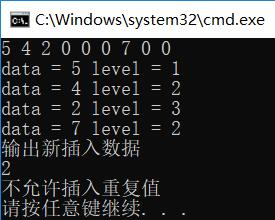
3、刪除節點
刪除節點的操作相對查找和插入要相對複雜一些,主要考慮以下三種情況(前兩種情況操作較為簡單,第三種較為複雜)

在刪除操作前先用要找到待刪除節點的位置(這裡使用的遞歸,也可以改成迭代)

情形一:刪除葉子節點

因為刪除葉子節點不會破壞BST的結構,刪除葉子節點的操作較為簡單,步驟如下
1、判斷待刪除節點的左右子樹是否為空,如果都為空那麼就是葉子節點
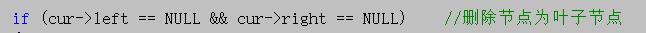
2、判斷待刪除節點是待刪除節點父節點的右子樹還是左子樹,將對應的指針賦值NULL

3、free待刪除節點

實現代碼:
1 /* 刪除節點 */ 2 /* cur為待刪除節點, parent為待刪除節點的父節點 */ 3 void DeletNode(BSTree *parent, BSTree *cur, int DelData) 4 { 5 BSTree *SNode = NULL; //後繼節點 6 BSTree *PSNode = NULL; //後繼節點的父節點 7 8 if (cur == NULL) 9 { 10 printf("刪除節點不存在n"); 11 exit(0); 12 } 13 else if (DelData > cur->data) 14 { 15 DeletNode(cur, cur->right, DelData); 16 } 17 else if (DelData < cur->data) 18 { 19 DeletNode(cur, cur->left, DelData); 20 } 21 else if(DelData == cur->data) 22 { 23 if (cur->left == NULL && cur->right == NULL) //待刪除節點為葉子節點 24 { 25 if (parent->left == cur) //如果該節點是父節點的左子樹 26 { 27 parent->left = NULL; 28 } 29 else if (parent->right == cur) //如果該節點是父節點的右子樹 30 { 31 parent->right = NULL; 32 } 33 }
因為刪除節點這個子函數我是用的不帶返回值的遞歸實現的,導致if else語句很多,後面我把刪除節點這個子函數改成帶返回值的遞歸,看起來要舒服不少,代碼如下,有興趣的讀者可以看一下

1 /* 刪除節點 */ 2 /* cur為待刪除節點, parent為待刪除節點的父節點 */ 3 BSTree *DeletNode(BSTree *parent, BSTree *cur, int DelData) 4 { 5 BSTree *SNode = NULL; //後繼節點 6 BSTree *PSNode = NULL; //後繼節點的父節點 7 BSTree *temp = NULL; //臨時保存待釋放節點的子樹,避免free後找不到左右子樹 8 9 if (cur == NULL) 10 { 11 printf("刪除節點不存在n"); 12 exit(0); 13 } 14 else if (DelData > cur->data) 15 { 16 cur->right = DeletNode(cur, cur->right, DelData); 17 } 18 else if (DelData < cur->data) 19 { 20 cur->left = DeletNode(cur, cur->left, DelData); 21 } 22 else if (DelData == cur->data) 23 { 24 if (cur->left == NULL && cur->right == NULL) //待刪除節點為葉子節點 25 { 26 free(cur); 27 return NULL; 28 }
帶返回值的遞歸實現
情形二:刪除帶有一個子節點的節點
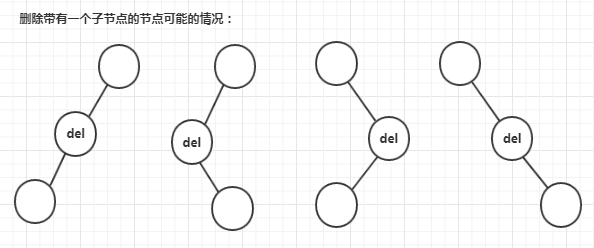
(圖片來源:https://www.cnblogs.com/songwenjie/p/8973217.html)
上圖寫了四種,但對待刪除節點來說只有兩種,只有左子樹,或只有右子樹,兩種情況的處理方式基本相同,都是將待刪除節點的左/右子樹 賦值給 待刪除節點的父節點的左/右子樹
實現代碼:
1 else if(cur->left != NULL && cur->right == NULL) //待刪除節點只有左子樹 2 { 3 if (parent->left == cur) 4 { 5 parent->left = cur->left; 6 } 7 else if (parent->right == cur) 8 { 9 parent->right = cur->left; 10 } 11 free(cur); //釋放待刪除節點 12 } 13 else if(cur->left == NULL && cur->right != NULL) //待刪除節點只有右子樹 14 { 15 if (parent->left == cur) 16 { 17 parent->left = cur->right; 18 } 19 else if (parent->right == cur) 20 { 21 parent->right = cur->right; 22 } 23 free(cur); //釋放待刪除節點 24 }

1 else if(cur->left != NULL && cur->right == NULL) //待刪除節點只有左子樹 2 { 3 temp = cur->left; 4 free(cur); 5 6 return temp;; 7 } 8 else if(cur->left == NULL && cur->right != NULL) //待刪除節點只有右子樹 9 { 10 temp = cur->right; 11 free(cur); 12 13 return cur->right; 14 }
帶返回值的遞歸實現
情形三:刪除帶兩個節點的節點
因為刪除節點會有破壞 BST 正確結構的風險,刪除帶兩個節點的節點操作顯得較為複雜,首先需要找到待刪除節點的 後繼節點 和 該後繼節點的父節點,(一個節點的後繼節點是指,這個節點在中序遍歷序列中的下一個節點,相應的,前驅節點是指這個節點在中序遍歷序列中的上一個節點),刪除節點的後繼節點一定是刪除節點右子樹的最左側節點,這篇隨筆採用的方式是後繼節點替代待刪除節點的方式而不是前驅節點替代刪除節點,需要考慮的情況如下

1、後繼節點為待刪除節點的子節點
在後繼節點為待刪除節點的子節點的前提下,該後繼節點有右子樹和沒有右子樹的操作是相同的,都是將 後繼節點 替代 待刪除節點,並將待刪除節點的左子樹 賦值給 後繼節點的左子樹
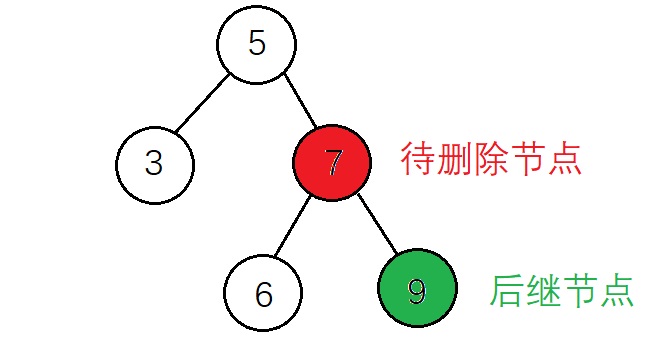
實現代碼:
1 else if(cur->left != NULL && cur->right != NULL) //待刪除節點既有左子樹也有右子樹 2 { 3 SNode = SearchSuccessorNode(cur->right); //搜索後繼節點 4 PSNode = SearchParentofSNode(cur->right, cur->right); //搜索後繼節點的父節點 5 6 if (cur->right == SNode) //後繼節點為待刪除節點的右子樹(後繼節點有右子樹和沒有右子樹的操作相同) 7 { 8 if (parent->left == cur) 9 { 10 parent->left = SNode; 11 SNode->left = cur->left; 12 13 free(cur); 14 } 15 else if (parent->right == cur) 16 { 17 parent->right = SNode; 18 SNode->left = cur->left; 19 20 free(cur); 21 } 22 }

1 else if(cur->left != NULL && cur->right != NULL) //待刪除節點既有左子樹也有右子樹 2 { 3 SNode = SearchSuccessorNode(cur->right); //搜索後繼節點 4 PSNode = SearchParentofSNode(cur->right, cur->right); //搜索後繼節點的父節點 5 6 if (cur->right == SNode) //後繼節點為待刪除節點的右子樹(後繼節點有右子樹和沒有右子樹的操作相同) 7 { 8 SNode->left = cur->left; 9 free(cur); 10 11 return SNode; 12 }
帶返回值的遞歸實現
2、後繼節點不為待刪除節點的子節點
這裡後繼節點還要在分為後繼節點有子節點和沒有子節點的情況
(1)後繼節點沒有右子節點
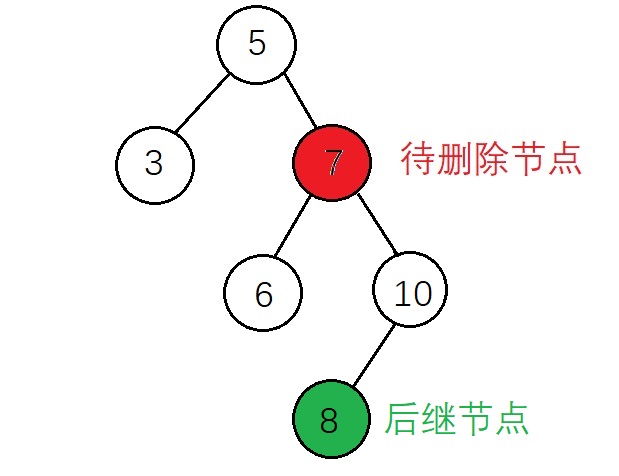

根據實現代碼來標註上面的節點
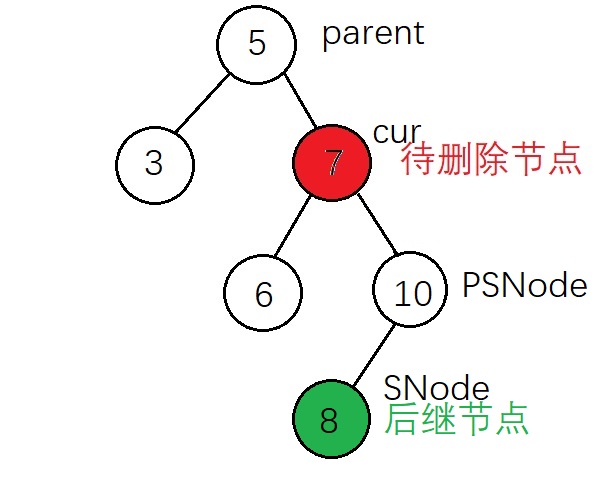
刪除後:
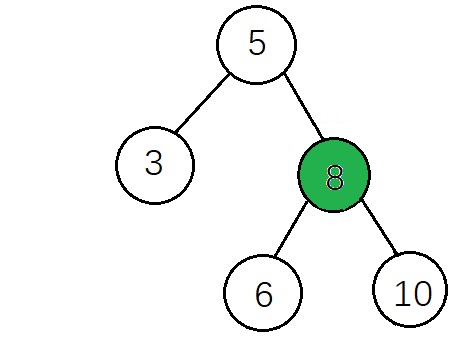
實現代碼:
1 else if (cur->right != SNode && SNode->right == NULL) //後繼節點不為待刪除節點的右子樹,並且該後繼節點沒有右子樹 2 { 3 if (parent->left == cur) 4 { 5 parent->left = SNode; 6 SNode->left = cur->left; 7 SNode->right = cur->right; 8 PSNode->left = NULL; 9 10 free(cur); 11 } 12 else if (parent->right == cur) 13 { 14 parent->right = SNode; 15 SNode->left = cur->left; 16 SNode->right = cur->right; 17 PSNode->left = NULL; 18 19 free(cur); 20 } 21 }

1 else if (cur->right != SNode && SNode->right == NULL) //後繼節點不為待刪除節點的右子樹,並且該後繼節點沒有右子樹 2 { 3 SNode->left = cur->left; 4 SNode->right = cur->right; 5 PSNode->left = NULL; 6 free(cur); 7 8 return SNode; 9 }
帶返回值的遞歸實現
(2)後繼節點有右子節點
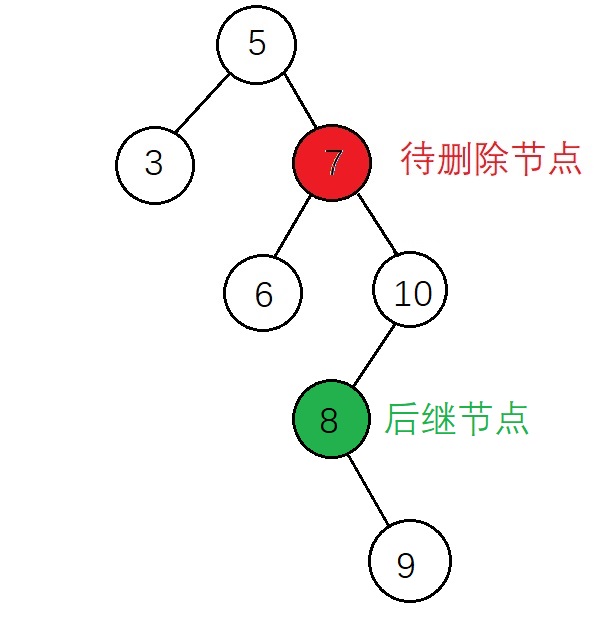
刪除後:

與上面的後繼節點沒有右子節點相比需要增加一個操作,需要將後繼節點的右子樹 賦值給 後繼節點的父節點的左子樹
實現代碼:
1 else if (cur->right != SNode && SNode->right != NULL) //後繼節點不為待刪除節點的右子樹,並且該後繼節點有右子樹 2 { 3 if (parent->left == cur) 4 { 5 parent->left = SNode; 6 PSNode->left = SNode->right; //後繼節點的右子樹作為後繼節點父節點的左子樹 7 SNode->left = cur->left; 8 SNode->right = cur->right; 9 10 free(cur); 11 } 12 else if (parent->right == cur) 13 { 14 parent->right = SNode; 15 PSNode->left = SNode->right; //後繼節點的右子樹作為後繼節點父節點的左子樹 16 SNode->left = cur->left; 17 SNode->right = cur->right; 18 19 free(cur); 20 } 21 }

1 else if (cur->right != SNode && SNode->right != NULL) //後繼節點不為待刪除節點的右子樹,並且該後繼節點有右子樹 2 { 3 4 PSNode->left = SNode->right; //後繼節點的右子樹作為後繼節點父節點的左子樹 5 SNode->left = cur->left; 6 SNode->right = cur->right; 7 free(cur); 8 9 return SNode; 10 }
帶返回值的遞歸實現
測試數據:
一、“後繼節點是刪除節點的子節點”(因為後繼節點有無子樹的操作相同,這裡只測試沒有子樹的情況)
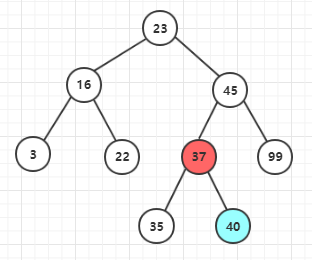

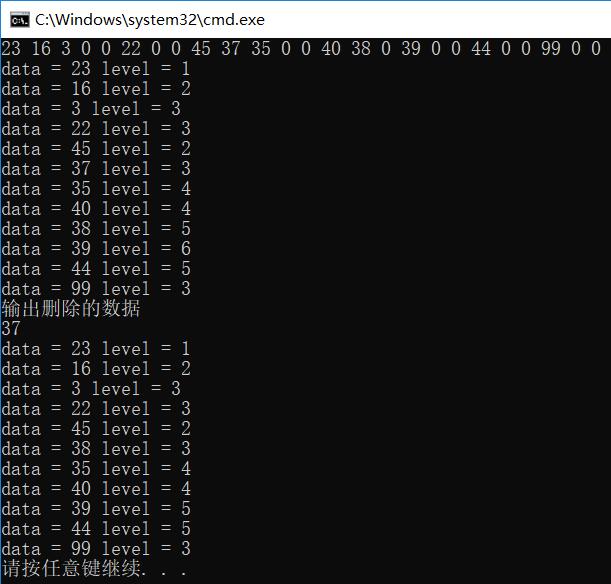
二、“後繼節點不是刪除節點的子節點,且後繼節點沒有右子樹”
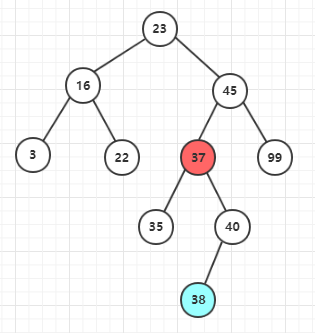

三、“後繼節點不是刪除節點的子節點,且後繼節點有右子樹”
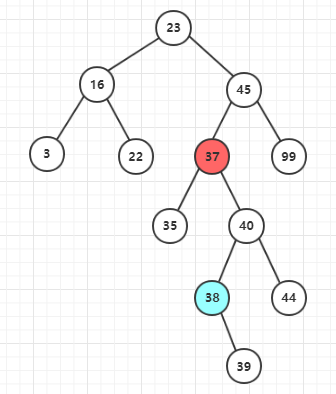
完整代碼:(註:對free(cur)的位置進行了調整)

1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <conio.h> 4 5 #define LEFT 1 6 #define RIGHT 2 7 8 typedef struct BSTreeNode 9 { 10 int data; 11 struct BSTreeNode *left;//左子樹 12 struct BSTreeNode *right;//右子樹 13 }BSTree; 14 15 BSTree *Create_BSTreeNode(BSTree *nod); //創建二叉查找樹 16 void PreOrder_Traverse(BSTree *nod, int level); //前序遍歷二叉樹,並打印 17 void SearchData(int targ, BSTree *nod); //查找特定值 18 BSTree *AddNewNode(BSTree *cur, int NewData); //添加新的節點 19 void DeletNode(BSTree *parent, BSTree *cur, int DelData); //刪除節點 20 BSTree *SearchSuccessorNode(BSTree *nod); //搜索後繼節點 21 BSTree *SearchParentofSNode(BSTree *Pnod, BSTree *nod); //搜索後繼節點的父節點 22 23 int main() 24 { 25 BSTree *nod = NULL; 26 //int num; 27 int key; 28 //int del; 29 30 nod = Create_BSTreeNode(nod); 31 PreOrder_Traverse(nod, 1); 32 33 //printf("輸出查找數據n"); 34 //scanf_s("%d", &num, 1); 35 //SearchData(num, nod); 36 37 printf("輸出新插入數據n"); 38 scanf_s("%d", &key, 1); 39 nod = AddNewNode(nod, key); 40 41 //printf("輸出刪除的數據n"); 42 //scanf_s("%d", &del, 1); 43 //DeletNode(nod, nod, del); 44 45 46 PreOrder_Traverse(nod, 1); 47 48 return 0; 49 } 50 51 /* 搜索後繼節點的父節點 */ 52 BSTree *SearchParentofSNode(BSTree *Pnod, BSTree *nod) 53 { 54 while (1) 55 { 56 if (nod->left != NULL) 57 { 58 Pnod = nod; 59 nod = nod->left; 60 } 61 else 62 { 63 break; 64 } 65 } 66 67 return Pnod; 68 } 69 70 /* 搜索後繼節點 */ 71 BSTree *SearchSuccessorNode(BSTree *nod) 72 { 73 while (1) 74 { 75 if (nod->left != NULL) 76 { 77 nod = nod->left; 78 } 79 else 80 { 81 break; 82 } 83 } 84 85 return nod; 86 } 87 88 /* 刪除節點 */ 89 /* cur為待刪除節點, parent為待刪除節點的父節點 */ 90 void DeletNode(BSTree *parent, BSTree *cur, int DelData) 91 { 92 BSTree *SNode = NULL; //後繼節點 93 BSTree *PSNode = NULL; //後繼節點的父節點 94 95 if (DelData > cur->data) 96 { 97 DeletNode(cur, cur->right, DelData); 98 } 99 else if (DelData < cur->data) 100 { 101 DeletNode(cur, cur->left, DelData); 102 } 103 else if(DelData == cur->data) 104 { 105 if (cur->left == NULL && cur->right == NULL) //待刪除節點為葉子節點 106 { 107 if (parent->left == cur) //如果該節點是父節點的左子樹 108 { 109 parent->left = NULL; 110 } 111 else if (parent->right == cur) //如果該節點是父節點的右子樹 112 { 113 parent->right = NULL; 114 } 115 } 116 else if(cur->left != NULL && cur->right == NULL) //待刪除節點只有左子樹 117 { 118 if (parent->left == cur) 119 { 120 parent->left = cur->left; 121 } 122 else if (parent->right == cur) 123 { 124 parent->right = cur->left; 125 } 126 } 127 else if(cur->left == NULL && cur->right != NULL) //待刪除節點只有右子樹 128 { 129 if (parent->left == cur) 130 { 131 parent->left = cur->right; 132 } 133 else if (parent->right == cur) 134 { 135 parent->right = cur->right; 136 } 137 } 138 else if(cur->left != NULL && cur->right != NULL) //待刪除節點既有左子樹也有右子樹 139 { 140 SNode = SearchSuccessorNode(cur->right); //搜索後繼節點 141 PSNode = SearchParentofSNode(cur->right, cur->right); //搜索後繼節點的父節點 142 143 if (cur->right == SNode) //後繼節點為待刪除節點的右子樹(後繼節點有右子樹和沒有右子樹的操作相同) 144 { 145 if (parent->left == cur) 146 { 147 parent->left = SNode; 148 SNode->left = cur->left; 149 } 150 else if (parent->right == cur) 151 { 152 parent->right = SNode; 153 SNode->left = cur->left; 154 } 155 } 156 else if (cur->right != SNode && SNode->right == NULL) //後繼節點不為待刪除節點的右子樹,並且該後繼節點沒有右子樹 157 { 158 if (parent->left == cur) 159 { 160 parent->left = SNode; 161 SNode->left = cur->left; 162 SNode->right = cur->right; 163 PSNode->left = NULL; 164 } 165 else if (parent->right == cur) 166 { 167 parent->right = SNode; 168 SNode->left = cur->left; 169 SNode->right = cur->right; 170 PSNode->left = NULL; 171 } 172 } 173 else if (cur->right != SNode && SNode->right != NULL) //後繼節點不為待刪除節點的右子樹,並且該後繼節點有右子樹 174 { 175 if (parent->left == cur) 176 { 177 parent->left = SNode; 178 PSNode->left = SNode->right; //後繼節點的右子樹作為後繼節點父節點的左子樹 179 SNode->left = cur->left; 180 SNode->right = cur->right; 181 } 182 else if (parent->right == cur) 183 { 184 parent->right = SNode; 185 PSNode->left = SNode->right; //後繼節點的右子樹作為後繼節點父節點的左子樹 186 SNode->left = cur->left; 187 SNode->right = cur->right; 188 } 189 } 190 } 191 free(cur); //釋放待刪除節點 192 } 193 } 194 195 /* 添加新節點 */ 196 BSTree *AddNewNode(BSTree *cur, int NewData) 197 { 198 if (cur == NULL) 199 { 200 if ((cur = (BSTree *)malloc(sizeof(BSTree))) == NULL) //創建新節點 201 { 202 printf("內存不足"); 203 exit(0); 204 } 205 cur->data = NewData; 206 cur->left = NULL; 207 cur->right = NULL; 208 209 return cur; 210 } 211 if (NewData > cur->data) 212 { 213 cur->right = AddNewNode(cur->right, NewData); 214 } 215 else if (NewData < cur->data) 216 { 217 cur->left = AddNewNode(cur->left, NewData); 218 } 219 else if (NewData == cur->data) 220 { 221 printf("不允許插入重複值n"); 222 exit(0); 223 } 224 225 return cur; 226 } 227 228 /* 查找特定值 */ 229 void SearchData(int targ, BSTree *nod) 230 { 231 if (nod != NULL) 232 { 233 if (nod->data == targ) 234 { 235 printf("查找值存在,值為%dn", nod->data); 236 } 237 else if (nod->data > targ) 238 { 239 SearchData(targ, nod->left); //遞歸查找左子樹 240 } 241 else if (nod->data < targ) 242 { 243 SearchData(targ, nod->right); //遞歸查找右子樹 244 } 245 } 246 else if (nod == NULL) 247 { 248 printf("查找值不存在n"); 249 } 250 } 251 252 /* 創建二叉查找樹(數據以前序遍歷順序輸入)*/ 253 BSTree *Create_BSTreeNode(BSTree *nod) 254 { 255 int num; 256 257 scanf_s("%d", &num, 1); 258 if (num == 0) /* 假定輸入的數據都為正數,以0作為NULL的標誌 */ 259 { 260 return NULL; 261 } 262 else 263 { 264 if ((nod = (BSTree *)malloc(sizeof(BSTree))) == NULL) 265 { 266 printf("內存空間不足"); 267 exit(0); 268 } 269 nod->data = num; 270 nod->left = Create_BSTreeNode(nod->left); 271 nod->right = Create_BSTreeNode(nod->right); 272 273 return nod; 274 } 275 } 276 277 /* 前序遍歷二叉樹,並打印 */ 278 void PreOrder_Traverse(BSTree *nod, int level) 279 { 280 if (nod == NULL) 281 { 282 return ; 283 } 284 285 printf("data = %d level = %dn", nod->data, level); 286 PreOrder_Traverse(nod->left, level + 1); 287 PreOrder_Traverse(nod->right, level + 1); 288 }
View Code
因為主要是分析二叉查找樹的查找、插入、刪除操作,沒有考慮二叉樹為空 或 待刪除節點為根節點的情況
補充:(註:刪除節點函數修改成了帶返回值的遞歸實現——更新日期2019/8/13)

1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <conio.h> 4 5 #define LEFT 1 6 #define RIGHT 2 7 8 typedef struct BSTreeNode 9 { 10 int data; 11 struct BSTreeNode *left;//左子樹 12 struct BSTreeNode *right;//右子樹 13 }BSTree; 14 15 BSTree *Create_BSTreeNode(BSTree *nod); //創建二叉查找樹 16 void PreOrder_Traverse(BSTree *nod, int level); //前序遍歷二叉樹,並打印 17 void SearchData(int targ, BSTree *nod); //查找特定值 18 BSTree *AddNewNode(BSTree *cur, int NewData); //添加新的節點 19 BSTree *DeletNode(BSTree *parent, BSTree *cur, int DelData); //刪除節點 20 BSTree *SearchSuccessorNode(BSTree *nod); //搜索後繼節點 21 BSTree *SearchParentofSNode(BSTree *Pnod, BSTree *nod); //搜索後繼節點的父節點 22 23 int main() 24 { 25 BSTree *nod = NULL; 26 //int num; 27 //int key; 28 int del; 29 30 nod = Create_BSTreeNode(nod); 31 PreOrder_Traverse(nod, 1); 32 33 /*printf("輸出查找數據n"); 34 scanf_s("%d", &num, 1); 35 SearchData(num, nod);*/ 36 37 /*printf("輸出新插入數據n"); 38 scanf_s("%d", &key, 1); 39 nod = AddNewNode(nod, key);*/ 40 41 printf("輸出刪除的數據n"); 42 scanf_s("%d", &del, 1); 43 nod = DeletNode(nod, nod, del); 44 45 46 PreOrder_Traverse(nod, 1); 47 48 return 0; 49 } 50 51 /* 搜索後繼節點的父節點 */ 52 BSTree *SearchParentofSNode(BSTree *Pnod, BSTree *nod) 53 { 54 while (1) 55 { 56 if (nod->left != NULL) 57 { 58 Pnod = nod; 59 nod = nod->left; 60 } 61 else 62 { 63 break; 64 } 65 } 66 67 return Pnod; 68 } 69 70 /* 搜索後繼節點 */ 71 BSTree *SearchSuccessorNode(BSTree *nod) 72 { 73 while (1) 74 { 75 if (nod->left != NULL) 76 { 77 nod = nod->left; 78 } 79 else 80 { 81 break; 82 } 83 } 84 85 return nod; 86 } 87 88 /* 刪除節點 */ 89 /* cur為待刪除節點, parent為待刪除節點的父節點 */ 90 BSTree *DeletNode(BSTree *parent, BSTree *cur, int DelData) 91 { 92 BSTree *SNode = NULL; //後繼節點 93 BSTree *PSNode = NULL; //後繼節點的父節點 94 BSTree *temp = NULL; //臨時保存待釋放節點的子樹,避免free後找不到左右子樹 95 96 if (cur == NULL) 97 { 98 printf("刪除節點不存在n"); 99 exit(0); 100 } 101 else if (DelData > cur->data) 102 { 103 cur->right = DeletNode(cur, cur->right, DelData); 104 } 105 else if (DelData < cur->data) 106 { 107 cur->left = DeletNode(cur, cur->left, DelData); 108 } 109 else if (DelData == cur->data) 110 { 111 if (cur->left == NULL && cur->right == NULL) //待刪除節點為葉子節點 112 { 113 free(cur); 114 return NULL; 115 } 116 else if(cur->left != NULL && cur->right == NULL) //待刪除節點只有左子樹 117 { 118 temp = cur->left; 119 free(cur); 120 121 return temp;; 122 } 123 else if(cur->left == NULL && cur->right != NULL) //待刪除節點只有右子樹 124 { 125 temp = cur->right; 126 free(cur); 127 128 return cur->right; 129 } 130 else if(cur->left != NULL && cur->right != NULL) //待刪除節點既有左子樹也有右子樹 131 { 132 SNode = SearchSuccessorNode(cur->right); //搜索後繼節點 133 PSNode = SearchParentofSNode(cur->right, cur->right); //搜索後繼節點的父節點 134 135 if (cur->right == SNode) //後繼節點為待刪除節點的右子樹(後繼節點有右子樹和沒有右子樹的操作相同) 136 { 137 SNode->left = cur->left; 138 free(cur); 139 140 return SNode; 141 } 142 else if (cur->right != SNode && SNode->right == NULL) //後繼節點不為待刪除節點的右子樹,並且該後繼節點沒有右子樹 143 { 144 SNode->left = cur->left; 145 SNode->right = cur->right; 146 PSNode->left = NULL; 147 free(cur); 148 149 return SNode; 150 } 151 else if (cur->right != SNode && SNode->right != NULL) //後繼節點不為待刪除節點的右子樹,並且該後繼節點有右子樹 152 { 153 154 PSNode->left = SNode->right; //後繼節點的右子樹作為後繼節點父節點的左子樹 155 SNode->left = cur->left; 156 SNode->right = cur->right; 157 free(cur); 158 159 return SNode; 160 } 161 } 162 } 163 164 return cur; 165 } 166 167 /* 添加新節點 */ 168 BSTree *AddNewNode(BSTree *cur, int NewData) 169 { 170 if (cur == NULL) 171 { 172 if ((cur = (BSTree *)malloc(sizeof(BSTree))) == NULL) //創建新節點 173 { 174 printf("內存不足"); 175 exit(0); 176 } 177 cur->data = NewData; 178 cur->left = NULL; 179 cur->right = NULL; 180 181 return cur; 182 } 183 if (NewData > cur->data) 184 { 185 cur->right = AddNewNode(cur->right, NewData); 186 } 187 else if (NewData < cur->data) 188 { 189 cur->left = AddNewNode(cur->left, NewData); 190 } 191 else if (NewData == cur->data) 192 { 193 printf("不允許插入重複值n"); 194 exit(0); 195 } 196 197 return cur; 198 } 199 200 /* 查找特定值 */ 201 void SearchData(int targ, BSTree *nod) 202 { 203 if (nod != NULL) 204 { 205 if (nod->data == targ) 206 { 207 printf("查找值存在,值為%dn", nod->data); 208 } 209 else if (nod->data > targ) 210 { 211 SearchData(targ, nod->left); //遞歸查找左子樹 212 } 213 else if (nod->data < targ) 214 { 215 SearchData(targ, nod->right); //遞歸查找右子樹 216 } 217 } 218 else if (nod == NULL) 219 { 220 printf("查找值不存在n"); 221 } 222 } 223 224 /* 創建二叉查找樹(數據以前序遍歷順序輸入)*/ 225 BSTree *Create_BSTreeNode(BSTree *nod) 226 { 227 int num; 228 229 scanf_s("%d", &num, 1); 230 if (num == 0) /* 假定輸入的數據都為正數,以0作為NULL的標誌 */ 231 { 232 return NULL; 233 } 234 else 235 { 236 if ((nod = (BSTree *)malloc(sizeof(BSTree))) == NULL) 237 { 238 printf("內存空間不足"); 239 exit(0); 240 } 241 nod->data = num; 242 nod->left = Create_BSTreeNode(nod->left); 243 nod->right = Create_BSTreeNode(nod->right); 244 245 return nod; 246 } 247 } 248 249 /* 前序遍歷二叉樹,並打印 */ 250 void PreOrder_Traverse(BSTree *nod, int level) 251 { 252 if (nod == NULL) 253 { 254 return ; 255 } 256 257 printf("data = %d level = %dn", nod->data, level); 258 PreOrder_Traverse(nod->left, level + 1); 259 PreOrder_Traverse(nod->right, level + 1); 260 }
View Code

