Stanford公開課《編譯原理》學習筆記(2)遞歸下降法
- 2019 年 10 月 7 日
- 筆記
目錄
示例代碼託管在:http://www.github.com/dashnowords/blogs
博客園地址:《大史住在大前端》原創博文目錄
華為雲社區地址:【你要的前端打怪升級指南】
B站地址:【編譯原理】
Stanford公開課:【Stanford大學公開課官網】
課程里涉及到的內容講的還是很清楚的,但個別地方有點脫節,建議課下自己配合經典著作《Compilers-priciples, Techniques and Tools》(也就是大名鼎鼎的龍書)作為補充閱讀。
一. Parse階段
詞法分析階段的任務是將字符串轉為Token組,而Parse階段的目標是將Token變為Parse Tree,本篇只是這部分內容最基礎的一部分。
CFG
CFG即context free grammer,定義一種CFG語法規則需要聲明如下特徵:

- 一組終止符號集,也稱為「詞法單元」
- 一組非終止符號集,也稱為「語法變量」
- 一個開始符號集
- 若干產生式規則(產生式則就是指在當前
CFG的語法下,產生符號->左右兩側可以互相替代)
CFG的基本轉換流程如下:
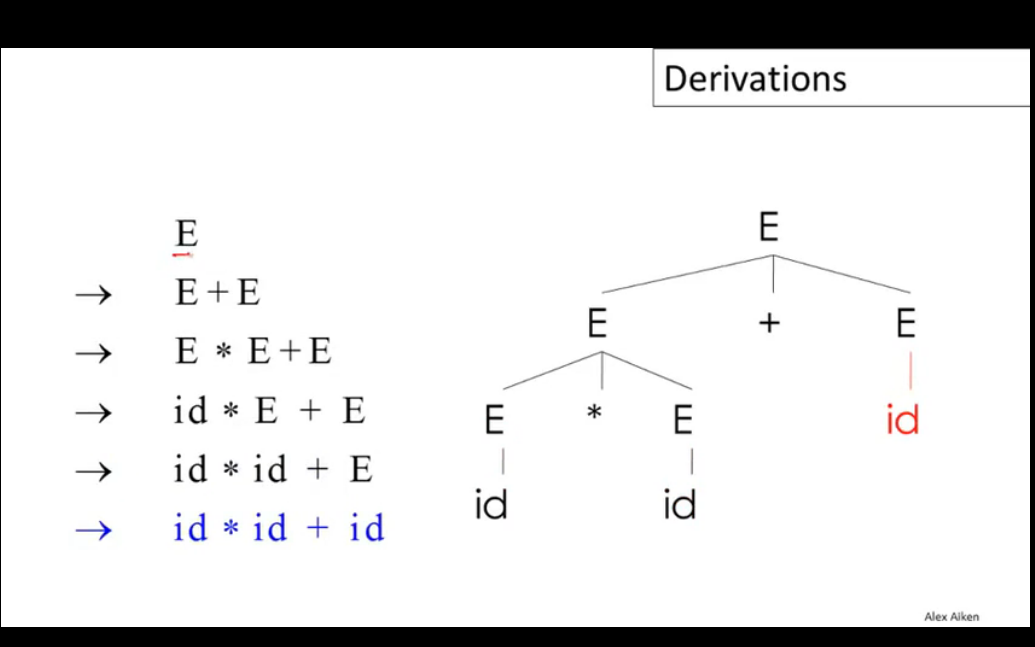
從隸屬於開始集S開始,嘗試將字符串中的非終止符X替換為終止集的形式(X->Y1Y2...Yn),重複這個步驟直到字符串序列中不再有非終止符。這個過程被稱為Derivation(派生),它是一系列變換過程的序列,可以轉換為樹的形式,樹的根節點即為起始集合S中的成員,轉換後的每個終止集以子節點的形式掛載在根節點下,這棵生成的樹就被稱為Parse Tree,可以看出最後的結果實際上就是Parse Tree的葉節點遍歷結果。
當需要轉換的非終結字符有多個時,需要按照一定的順序來逐個推導,派生過程可以按照left-most或right-most進行,但有時會得到不同的合法的轉換樹,通常會通過修改轉換集語法或設定優先級來解決。
Recursive Descent(遞歸下降遍歷)
Recursive Descent是一種遍歷parse tree的策略,是一種典型的遞歸回溯算法,從樹的根節點開始,逐個嘗試當前父節點上記錄的非終止字符能夠支持的產生規則,並判斷其子節點是否符合這樣的形式,直到子節點符合某個特定的產生式規則,然後再繼續遞歸進行深度遍歷,如果在某個非終止節點上嘗試完所有的產生式規則都無法繼續向下進行使得子樹的葉節點都符合終止符號集,則需要通過回溯到上一節點並嘗試父節點的下一個產生式規則,使得循環程序可以繼續向後進行。課程里用了很多的數學符號定義和偽代碼來描述遞歸遍歷的過程,如果覺得太抽象不好理解可以暫時略過。需要注意左遞歸文法會使得遞歸下降遍歷進入死循環,在文法設計時應該避免,龍書中也提供了一種通用的拆分方法來解決這個問題。
二. 遞歸下降遍歷
【聲明】由於課程中並沒有看到從
tokens到parse tree的全貌,只能先逐步消化基礎知識。下文的過程只是筆者自己的理解(尤其是逐行分析的形式,因為尚未涉及任何結構性語法,所以通用性還有待考量),僅供參考,也歡迎交流指正。但對於直觀理解遞歸下降法而言是足夠的。
2.1 預備知識
本節中使用JavaScript來實現遞歸下降遍歷,目標代碼仍是上一篇博文中的示例代碼:
var b3 = 2; a = 1 + ( b3 + 4); return a;經過上一節的分詞器後可以得到下面的詞素序列:
[ 'keywords', 'var' ], [ 'id', 'b3' ], [ 'assign', '=' ], [ 'num', '2' ], [ 'semicolon', ';' ], [ 'id', 'a' ], [ 'assign', '=' ], [ 'num', '1' ], [ 'plus', '+' ], [ 'lparen', '(' ], [ 'id', 'b3' ], [ 'plus', '+' ], [ 'num', '4' ], [ 'rparen', ')' ], [ 'semicolon', ';' ], [ 'keywords', 'return' ], [ 'id', 'a' ], [ 'semicolon', ';' ]語法分析是基於語法規則的,所謂語法規則,通常是指一系列CFG表示的產生式,大多數開發者並不具備設計一套語法規則的能力,此處直接借鑒Mozilla中的Javascript引擎SpiderMonkey中的文法定義來進行基本產生式,由於Javascript語言中涉及的文法非常多,本節只篩選出與目標解析式相關的一部分簡化的語法規則(圖中標記為藍色的部分):
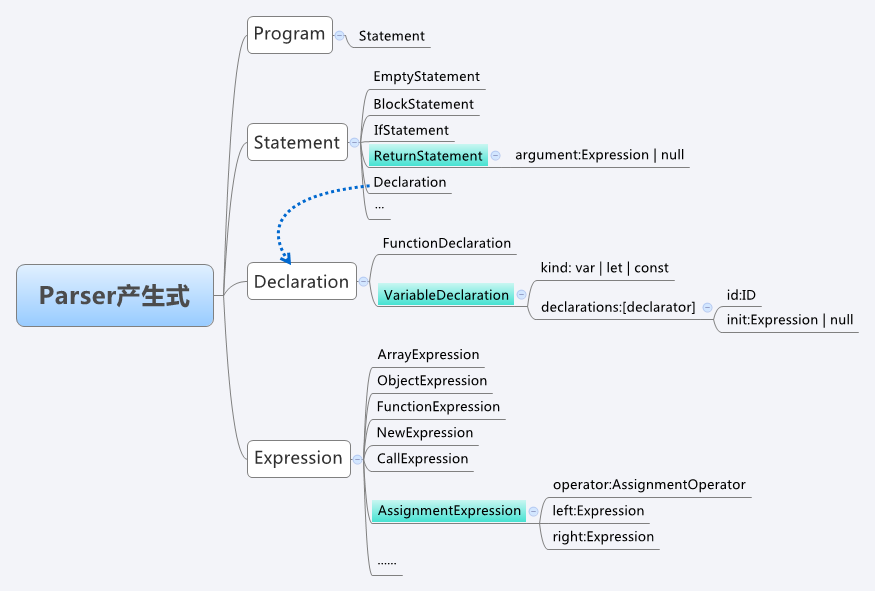
完整的語法規則可以查看【SpiderMonkey_ParserAPI】進行了解。
2.2 多行語句的處理思路
我們把上面的目標解析代碼當做是一段Javascript代碼,自頂向下分析時,根節點的類型是Program,它可以由多個Statement節點(語句節點)構成,所以本例中進行簡化後以semicolon(分號)作為詞素批量處理的分界點,每次將兩個分號之間的部分讀入緩衝區進行分析,由於上例中均為單行語句,所以理解起來比較簡單。
在更為複雜的情況中,代碼中包含條件語句,循環語句等一些結構化的關鍵詞時可能會存在跨行的語句,此時可以在遞歸下降之前先對緩衝區的詞素隊列進行基本的結構分析,如果發現匹配的結構化模式,就從tokens序列中將下一行(或多行)也讀入緩衝區,直到緩衝區中的所有tokens放在一起符合了某些特定的結構,再開始進行遞歸下降。
2.3 簡易的文法定義
為方便理解,本例中均使用關鍵詞縮寫來表示可能的語法規則集,如果你對Javascript語言有一定了解,它們是非常容易理解的
/** * 文法定義-生產規則 * Program -> Statement * P -> S * * 語句 -> 塊狀語句 | if語句 | return語句 | 聲明 | 表達式 |...... * Statement -> BlockStatement | IfStatement | ReturnStatement | Declaration | Expression |...... * S -> B | I | R | D | E * * B -> { Statement } * * I -> if ( ExpressionStatement ) { Statement } * * R -> return Expression | null * * 聲明 -> 函數聲明 | 變量聲明 * Declaration -> FunctionDeclaration | VariableDeclaration * D -> F | V * * F -> function ID ( SequenceExpression ) { ... } * * V -> 'var | let | const' ID [= Expression | Null] ? * * 表達式 -> 賦值表達式 | 序列表達式 | 一元運算表達式 | 二元運算表達式 |...... * Expression -> AssignmentExpression | SequenceExpression | UnaryExpression | BinaryExpression | BracketExpression...... * E -> A | Seq | U | BI | BRA |... * * A -> E = E //賦值表達式 * * Seq -> ID,ID,ID//類似形式 * * //一元表達式 * U -> "-" | "+" | "!" | "~" | "typeof" | "void" | "delete" E * * //二元表達式 * BI -> E "==" | "!=" | "===" | "!==" | "<" | "<=" | ">" | ">=" | "<<" | ">>" | ">>>" | "+" | "-" | "*" | "/" | "%" | "|" | "^" | "&" | "in" | "instanceof" | ".." E * * //括號表達式 * BRA -> ( E ) * * N -> null */需要額外注意的是表達式Expression到賦值表達式AssignmentExpression的產生式,E的判斷規則里需要判斷A,而A的邏輯里又再次調用了E,這裡就是一種左遞歸,如果不進行任何處理,在代碼運行時就會陷入死循環然後爆棧,這也就是前文強調的需要在語法產生式設計時消除左遞歸的場景。這裡並不是說spiderMonkey的parserAPI是錯的,因為消除左遞歸的語法改造只是一種等價形式的轉換,是為了防止產生式產生無限遞推(或者說程序實現時進入無限遞歸的死循環)而做的一種形式處理,改造的過程可能只是引入了某個中間集合來消除這種場景的影響,對於最終的語法表意並不會產生影響。
下文示例代碼中並沒有進行嚴謹的"左遞歸消除",而是簡單地使用了一個E_集合,與原本的E進行一些微小的差異區分,從而避免了死循環。
2.4 文法產生式的代碼轉換
下面將上一小節的語法規則進行代碼翻譯(只包含部分產生式的推導,本例中的完整代碼可以從demo或代碼倉中獲取):
//判斷是否為Statement function S(tokens) { //把結尾的分號全部去除 while(tokens[tokens.length - 1][0] === TT.semicolon){ tokens.pop(); } return B(tokens) || I(tokens) || R(tokens) || D(tokens) || E(tokens); } //判斷是否為BlockStatement B -> { Statement } (本例中並不涉及本方法,故暫不考慮末尾分號和文法遞歸的情況) function B(tokens) { //本例中不涉及,直接返回false return false; } //判斷是否為IfStatement I -> if ( ExpressionStatement ) { Statement } function I(tokens) { //本例中不涉及,直接返回false return false; } //判斷是否為ReturnStatement R -> return Expression | null function R(tokens) { return isReturn(tokens[0]) && (E(tokens.slice(1)) || N(tokens.slice(1)[0])); } //判斷是否為聲明語句 Declaration -> FunctionDeclaration | VariableDeclaration function D(tokens) { return F(tokens) || V(tokens); } //判斷是否為函數聲明 F -> function ID ( SequenceExpression ) { ... } function F(tokens) { //本例中不涉及,直接返回false return false; } //判斷是否為變量聲明 V -> 'var | let | const' ID [= Expression | Null] ? function V(tokens) { //判斷為1.單純的聲明 還是 2.帶有初始值的聲明 if (tokens.length === 2) { return isVariableDeclarationKeywords(tokens[0]) && tokens[1][0] === TT.id; } return isVariableDeclarationKeywords(tokens[0]) && (A(tokens.slice(1))) || N(tokens.slice(1)); } //....其他代碼形式雷同,不再贅述2.5 逐行解析
解析時默認每次遇到一個分號時表示一個statement的結束,前文已經提及過對於多行語句的處理思路。實現時只需要將tokens序列一點點讀進buffer數組並從頂層的S方法啟動分析,即可完成自頂向下的推理過程。
/**parser */ function parse(tokens) { let buffer = nextStatement(tokens); let flag = true; while (buffer && flag){ if (!S(buffer)) { console.log('檢測到不符合語法的tokens序列'); flag = false; } buffer = nextStatement(tokens); } //如果沒有出錯則提示正確 flag && console.log('檢測結束,被檢測tokens序列是合法的代碼段'); } //將下一個Statement全部讀入緩衝區 function nextStatement(tokens) { let result = []; let token; while(tokens.length) { token = tokens.shift(); result.push(token); //如果不是換行符則 if (token[0] === CRLF) { break; } } return result.length ? result : null; } 2.6 查看計算過程
單步執行查看計算過程可以幫助我們更好地理解遞歸下降法的執行過程:
在demo所在目錄下打開命令行,輸入:node --inspect-brk recursive-descent.js,然後單步執行就很容易看出代碼在執行過程中如何實現遞歸和回溯:
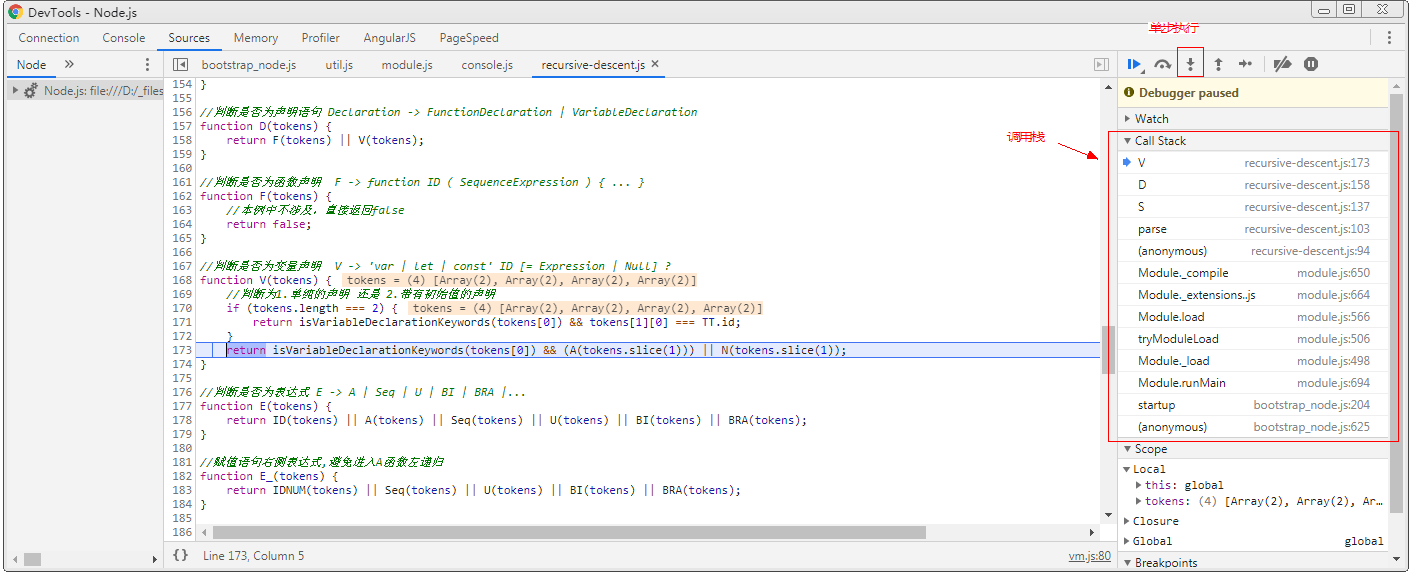
三.小結
單純地遞歸下降法最終的結果只找出了不滿足任何語法規則的語句,或是最終所有語句都符合語法規則時給出提示,但並沒有得到一個樹結構的對象,也沒有向下一個環節提供輸出,如何在編譯過程中與後續環節進行連接還有待探索。
