數據挖掘入門系列教程（十點五）之DNN介紹及公式推導

2020 年 4 月 27 日
筆記
數據挖掘

深度神經網絡(DNN，Deep Neural Networks)簡介

首先讓我們先回想起在之前博客（數據挖掘入門系列教程（七點五）之神經網絡介紹）中介紹的神經網絡：為了解決M-P模型中無法處理XOR等簡單的非線性可分的問題時，我們提出了多層感知機，在輸入層和輸出層中間添加一層隱含層，這樣該網絡就能以任意精度逼近任意複雜度的連續函數。

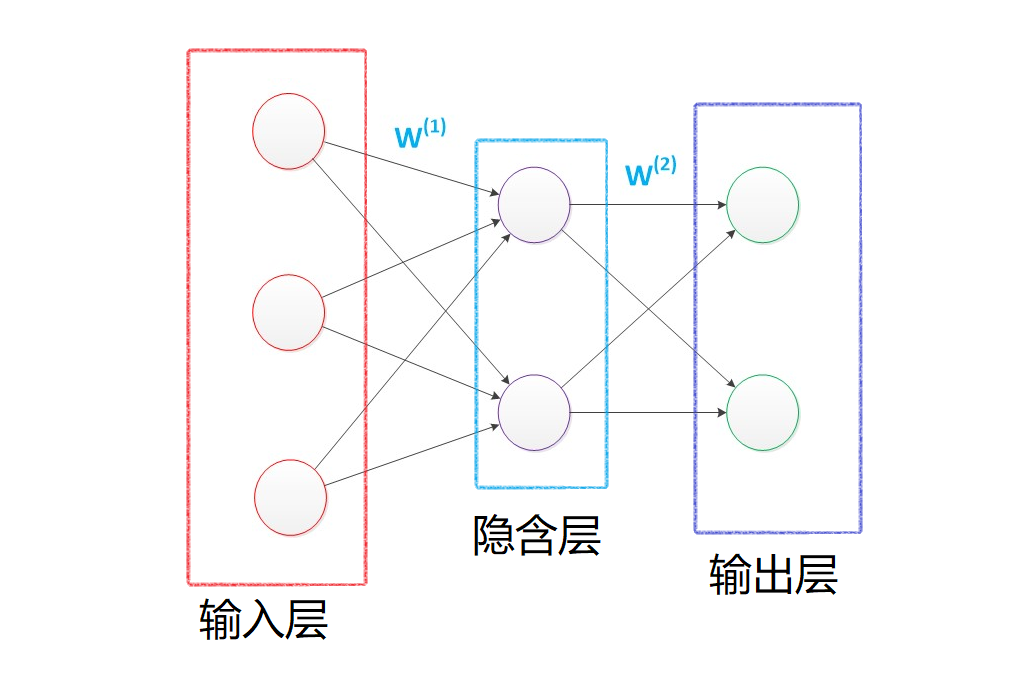
然後在數據挖掘入門系列教程（八）之使用神經網絡（基於pybrain）識別數字手寫集MNIST博客中，我們使用類似上圖的神經網絡結構對MINIST數據集進行了訓練，最後在epochs = 100的條件下，F1 socre達到了約$86\%$。

這個時候我們想一想，如果我們將中間的隱含層由一層變為多層，如下圖所示：

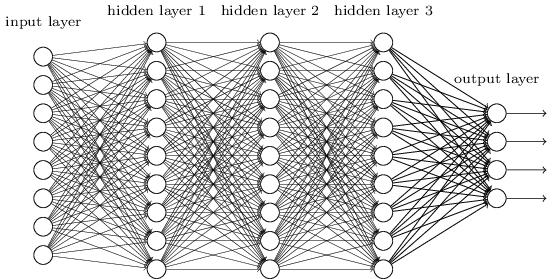
那麼該網絡就變成了深度神經網絡（DNN），也可以稱之為多層感知機（Multi-Layer perceptron,MLP）。

下面將對這個網絡進行介紹以及公式推導。

DNN的基本結構及前向傳播

在上面的圖中，我們可以很容易的觀察到，在DNN中，層與層之間是全連接的，也就是如同感知機一樣，第$i$層的任意一個神經元與第$i+1$層的任意一個神經元都有連接。儘管這個網絡看起來很龐大複雜，但是如果我們只看某一小部分，實際上它的原理與感知機很類似。

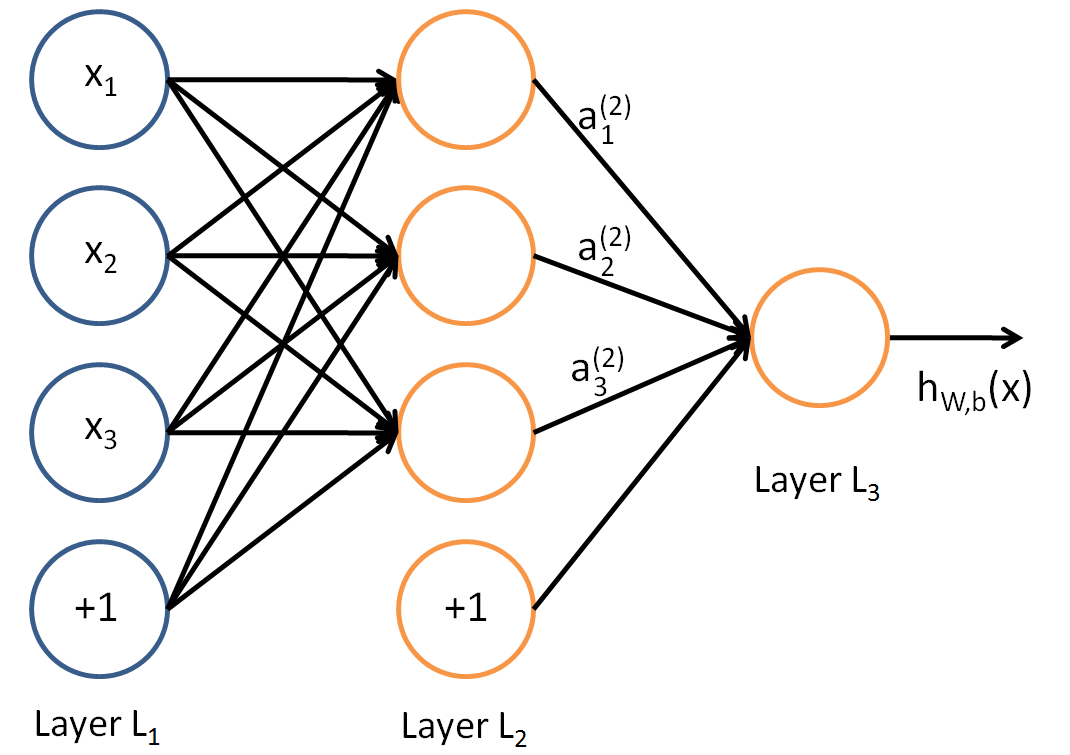
如同感知機，我們可以很簡單的知道：

對於$LayerL_2$的輸出，可知：

\[\begin{equation}\begin{aligned}
&a_{1}^{2}=\sigma\left(z_{1}^{2}\right)=\sigma\left(w_{11}^{2} x_{1}+w_{12}^{2} x_{2}+w_{13}^{2} x_{3}+b_{1}^{2}\right)\\
&\begin{array}{l}
a_{2}^{2}=\sigma\left(z_{2}^{2}\right)=\sigma\left(w_{21}^{2} x_{1}+w_{22}^{2} x_{2}+w_{23}^{2} x_{3}+b_{2}^{2}\right) \\
a_{3}^{2}=\sigma\left(z_{3}^{2}\right)=\sigma\left(w_{31}^{2} x_{1}+w_{32}^{2} x_{2}+w_{33}^{2} x_{3}+b_{3}^{2}\right)
\end{array}
\end{aligned}\end{equation}
\]

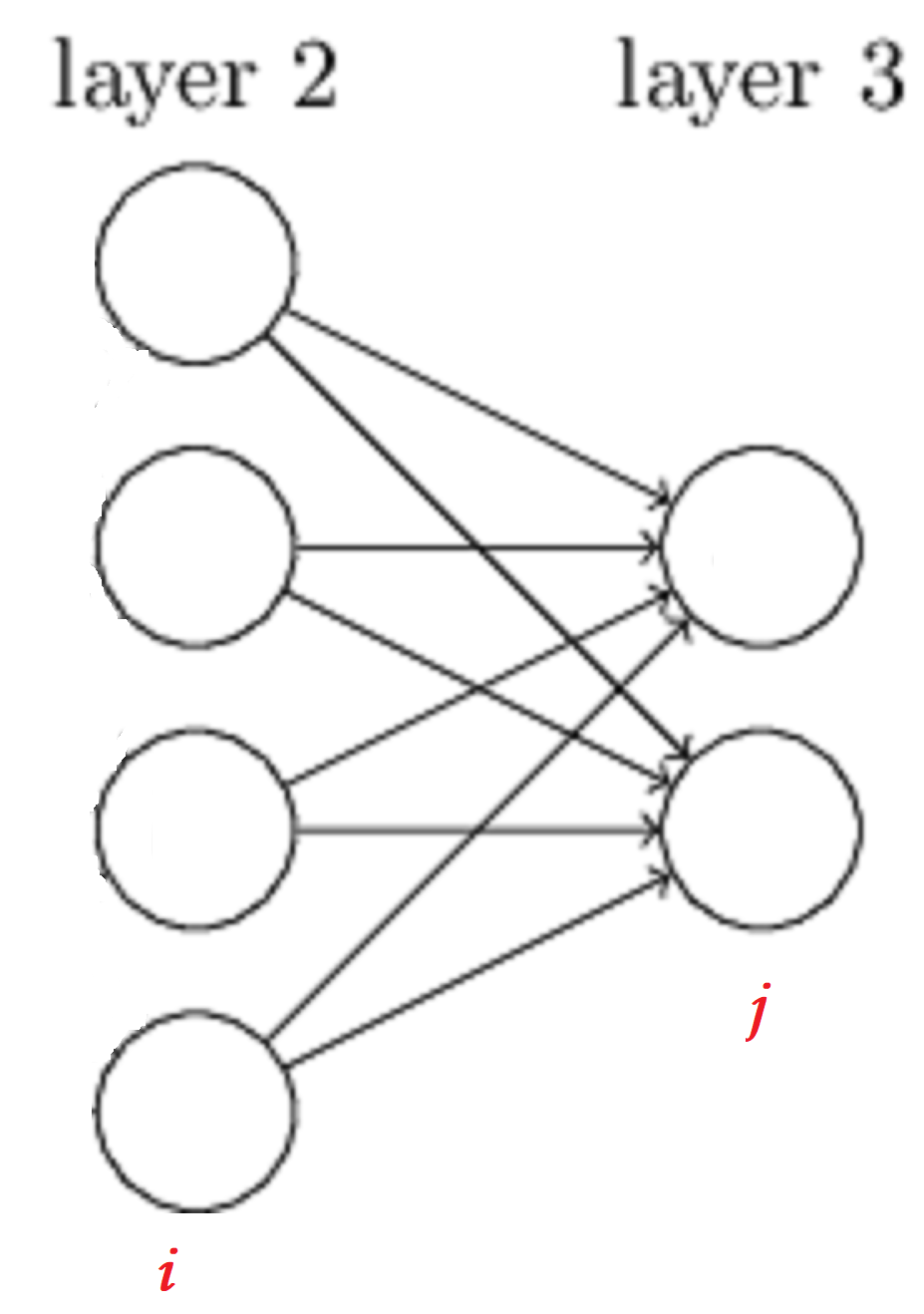
對於$w$的參數上標下標解釋，以下圖為例：

對於$w_{24}^3$，上標3代表$w$所在的層數，下標2對應的是第三層的索引2，下標4對應的是第二層的索引4。至於為什麼標記為$w_{24}^3$而不是$w_{42}^3$，我們可以從矩陣計算的角度進行考慮：

在下圖中，為了得到$a$，我們可以直接使用$a = Wx$，也可使用$a = W^Tx$這種形式，但是對於第二種形式，我們需要使用轉置，這樣會加大計算量，因此我們採用第一種形式。

對於$LayerL_3$的輸出，可知：

\[\begin{equation}a_{1}^{3}=\sigma\left(z_{1}^{3}\right)=\sigma\left(w_{11}^{3} a_{1}^{2}+w_{12}^{3} a_{2}^{2}+w_{13}^{3} a_{3}^{2}+b_{1}^{3}\right)\end{equation}
\]

假設我們在$l-1$層一共有$m$個神經元，對於第$l$層第$j$個神經元的輸出$a_j^l$，有：

\[\begin{equation}a_{j}^{l}=\sigma\left(z_{j}^{l}\right)=\sigma\left(\sum_{k=1}^{m} w_{j k}^{l} a_{k}^{l-1}+b_{j}^{l}\right)\end{equation}
\]

如果我們採用矩陣的方式進行表示，則第$l$層的輸出為：

\[a^l = \sigma(z^l) = \sigma(W^la^{l-1} + b^l)
\]

因此，我們可以對DNN的前向傳播算法進行推導，從輸入到輸出有：

輸入: 總層數$L$，所有隱藏層和輸出層對應的矩陣$W$,偏倚向量$b$，輸入值向量$x$

輸出：輸出層的輸出$a^L$

1）初始化$a^1 = x$

2) for $l=2$ to $L$，計算：

\[\begin{equation}a^{l}=\sigma\left(z^{l}\right)=\sigma\left(W^{l} a^{l-1}+b^{l}\right)\end{equation}
\]

最後結果的輸出即為$a^L$

以上便是DNN的前向傳播算法，實際上挺簡單的，就是一層一層向下遞歸。

DNN反向傳播（BP）算法

在數據挖掘入門系列教程（七點五）之神經網絡介紹中，我們提到過BP算法，並進行過詳細的數學公式的推導。BP算法的目的就是為了尋找合適的$W，b$使得損失函數$Loss$達到某一個比較小的值（極小值）。

在DNN中，損失函數優化極值求解的過程最常見的一般是通過梯度下降法來一步步迭代完成的，當然也有其他的方法。而在這裡，我們將使用梯度下降法對DNN中的反向傳播算法進行一定的數學公式推導。圖片和部分過程參考了Youtube：反向傳播算法，但是對其中的某一些圖片進行了修改。

在左邊的圖片中，是一個比較複雜的DNN網絡，我們針對該DNN網絡進行簡化，將其看成每一層只有一個神經元的網絡，如右圖所示

此時我們還可以將問題進行簡化，如果我們只看簡化模型的最後面兩個神經元，則有：

$y$代表期望值，$C_o$代表損失函數$\mathrm{C_0}=\operatorname{Loss}=\left(a^{(L)}-y\right)^{2}$，$\sigma$代表激活函數，比如說Relu，sigmoid，具體的表達式在圖中，我就不寫出來了。

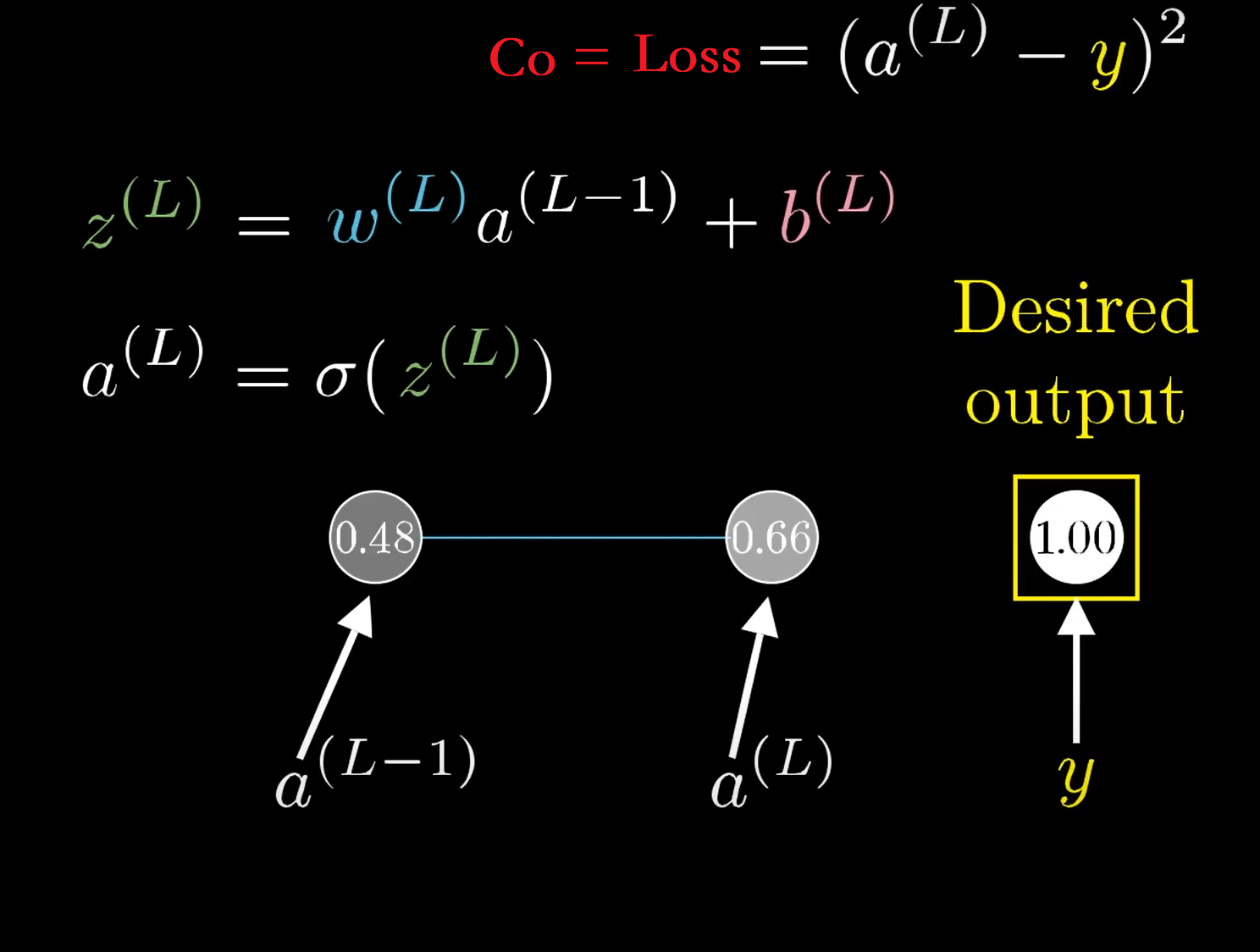
在下圖所示，當$w^{(L)}$發生微小的改變（$\partial w^{(L)}$）時，會通過一連串的反應使得$C_0$發生微小的改變：類似蝴蝶扇動翅膀一樣，響應流程如下$\partial w^{(L)} \longrightarrow z^{(L)} \longrightarrow a^{(L)} \longrightarrow C_0$。

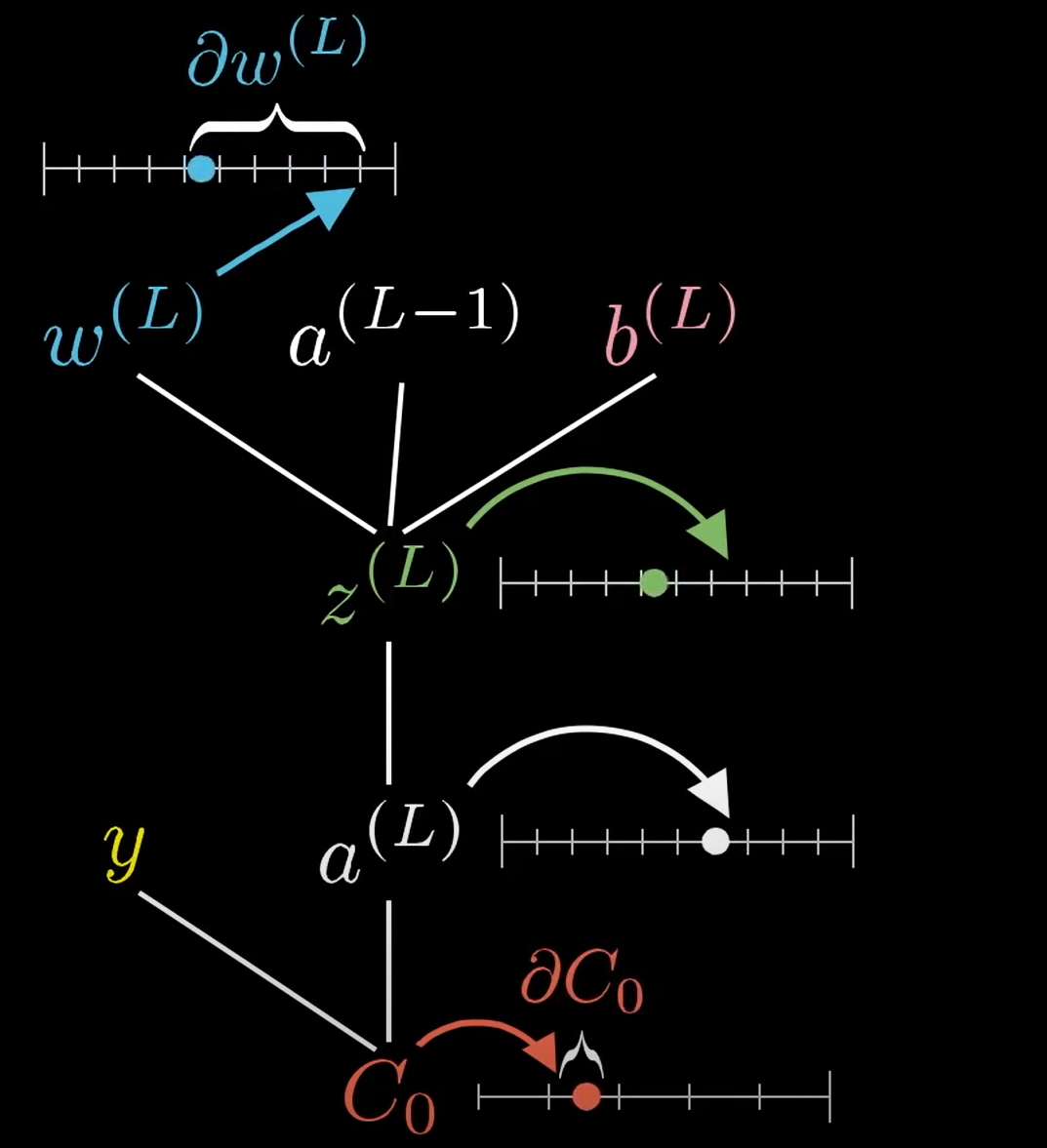
此時我們對$C_0$求其$W^L$的偏導，則得到了下式：

\[\begin{equation}\frac{\partial C_{0}}{\partial w^{(L)}}=\frac{\partial z^{(L)}}{\partial w^{(L)}} \frac{\partial a^{(L)}}{\partial z^{(L)}} \frac{\partial C_0}{\partial a^{(L)}}\end{equation}
\]

我們分別求各自偏導的結果：

\[\begin{equation}\begin{aligned}
&\because C_{0}=\left(a^{(L)}-y\right)^{2} \\
& \therefore \frac{\partial C 0}{\partial a^{(L)}}=2\left(a^{(L)}-y\right)\\
&\because a^{(L)}=\sigma\left(z^{(L)}\right) \\
& \therefore\frac{\partial a^{(L)}}{\partial z^{(L)}}=\sigma^{\prime}\left(z^{(L)}\right)\\
&\because z^{(L)}=w^{(L)} a^{(L-1)}+b^{(L)}\\
& \therefore \frac{\partial z^{(L)}}{\partial w^{(L)}}=a^{(L-1)}
\end{aligned}\end{equation}
\]

綜上，結果為：

\[\begin{equation}\frac{\partial C_{0}}{\partial w^{(L)}}=\frac{\partial z^{(L)}}{\partial w^{(L)}} \frac{\partial a^{(L)}}{\partial z^{(L)}} \frac{\partial C 0}{\partial a^{(L)}}=a^{(L-1)} \sigma^{\prime}\left(z^{(L)}\right) 2\left(a^{(L)}-y\right)\end{equation}
\]

同理我們可得：

\[\begin{equation}\frac{\partial C_{0}}{\partial b^{(L)}}=\frac{\partial z^{(L)}}{\partial b^{(L)}} \frac{\partial a^{(L)}}{\partial z^{(L)}} \frac{\partial C 0}{\partial a^{(L)}}=1 \sigma^{\prime}\left(z^{(L)}\right) 2\left(a^{(L)}-y\right)\end{equation}
\]

\[\begin{equation}\frac{\partial C_{0}}{\partial a^{(L-1)}}=\frac{\partial z^{(L)}}{\partial a^{(L-1)}} \frac{\partial a^{(L)}}{\partial z^{(L)}} \frac{\partial C 0}{\partial a^{(L)}}=w^{(L)} \sigma^{\prime}\left(z^{(L)}\right) 2\left(a^{(L)}-y\right)\end{equation}
\]

這時候，我們可以稍微將問題複雜化一點，考慮多個神經元如下圖所示，那麼此時所有的變量$W,x,b,z,a,y$也就變成了一個矩陣：

求導結果如下（這裡我們使得Loss為$J(W, b, x, y)=\frac{1}{2}\left\|a^{L}-y\right\|_{2}^{2}$表示，代表Loss與$W, b, x, y$有關）：

\[\begin{equation}\begin{array}{c}
\frac{\partial J(W, b, x, y)}{\partial W^{L}}=\frac{\partial J(W, b, x, y)}{\partial z^{L}} \frac{\partial z^{L}}{\partial W^{L}}=\frac{\partial J(W, b, x, y)}{\partial a^{L}} \frac{\partial a^{L}}{\partial z^{L}} \frac{\partial z^{L}}{\partial W^{L}}=\left(a^{L}-y\right) \odot \sigma^{\prime}\left(z^{L}\right)\left(a^{L-1}\right)^{T} \\
\frac{\partial J(W, b, x, y)}{\partial b^{L}}=\frac{\partial J(W, b, x, y)}{\partial z^{L}} \frac{\partial z^{L}}{\partial b^{L}}=\frac{\partial J(W, b, x, y)}{\partial a^{L}} \frac{\partial a^{L}}{\partial z^{L}} \frac{\partial z^{L}}{\partial b^{L}}=\left(a^{L}-y\right) \odot \sigma^{\prime}\left(z^{L}\right)
\end{array}\end{equation}
\]

注意上式中有一個符號$\odot$,它代表Hadamard積, 對於兩個維度相同的向量 $A\left(a_{1}, a_{2}, \ldots a_{n}\right)^T 和 B\left(b_{1}, b_{2}, \ldots b_{n}\right)^{T},$ 則 $A \odot B=$ $\left(a_{1} b_{1}, a_{2} b_{2}, \ldots a_{n} b_{n}\right)^{T}$。怎麼理解這個變量呢？從一個不怎麼嚴謹的角度進行理解：

假設第$L-1$層有$i$個神經元，第$L$層有$j$個神經元（如上圖所示），那麼毋庸置疑，$\partial W$為一個$j \times i$的矩陣（因為$W$為一個$j \times i$的矩陣，至於為什麼，前面前向傳播中已經提到了）。$A \odot B$則是一個$j \times 1$的矩陣，然後與$\left(a^{L-1}\right)^{T}$*（它是一個$1 \times i $的矩陣）*相乘，最後結果則為一個$j \times i$的矩陣。

在求導的結果$\frac{\partial J(W, b, x, y)}{\partial W^{L}} 和 \frac{\partial J(W, b, x, y)}{\partial b^{L}}$有公共部分，也就是$\frac{\partial J(W, b, x, y)}{\partial z^{L}}=\left(a^{L}-y\right) \odot \sigma^{\prime}\left(z^{L}\right)$，代表輸出層的梯度，因此我們令：

\[\begin{equation}\delta^{L}=\frac{\partial J(W, b, x, y)}{\partial z^{L}}=\left(a^{L}-y\right) \odot \sigma^{\prime}\left(z^{L}\right)\end{equation}
\]

根據前向傳播算法，對於與第$l$層的$W^l 和 b^l$的梯度有如下結論：

\[\begin{equation}\begin{array}{c}
\frac{\partial J(W, b, x, y)}{\partial W^{l}}=\frac{\partial J(W, b, x, y)}{\partial z^{l}} \frac{\partial z^{l}}{\partial W^{l}}=\delta^{l}\left(a^{l-1}\right)^{T} \\
\frac{\partial J(W, b, x, y)}{\partial b^{l}}=\frac{\partial J(W, b, x, y)}{\partial z^{l}} \frac{\partial z^{l}}{\partial b^{l}}=\delta^{l}
\end{array}\end{equation}
\]

因此問題就變成了如何求得任意一層$l$的$\delta^{l}$，假設我們一共有$L$層，則對於$\delta^{L}$我們還是能夠直接進行求解$\delta^{L}=\left(a^{L}-y\right) \odot \sigma^{\prime}\left(z^{L}\right)$，那麼我們如何對$L-1$層進行求解呢？

設第$l+1$層的$\delta^{l+1}$已知，則對$\delta^{l}$的求解如下：

\[\delta^{l} = \frac{\partial J(W,b,x,y)}{\partial z^l} = (\frac{\partial z^{l+1}}{\partial z^{l}})^T\frac{\partial J(W,b,x,y)}{\partial z^{l+1}} =(\frac{\partial z^{l+1}}{\partial z^{l}})^T \delta^{l+1}
\]

也就是說，求解關鍵點又到了$(\frac{\partial z^{l+1}}{\partial z^{l}})^T$的求解，根據前向傳播算法：

\[z^{l+1}= W^{l+1}a^{l} + b^{l+1} = W^{l+1}\sigma(z^l) + b^{l+1}
\]

因此，有：

\[\frac{\partial z^{l+1}}{\partial z^{l}} = W^{l+1}diag(\sigma^{‘}(z^l))
\]

綜上可得：

\[\delta^{l} = (\frac{\partial z^{l+1}}{\partial z^{l}})^T\frac{\partial J(W,b,x,y)}{\partial z^{l+1}} = diag(\sigma^{‘}(z^l))(W^{l+1})^T\delta^{l+1} =
(W^{l+1})^T\delta^{l+1}\odot \sigma^{‘}(z^l)
\]

因此當我們可以得到任意一層的$\delta^{l}$時，我們也就可以對任意的$W^l和b^l$進行求解。

算法流程

下面算法流程是copy深度神經網絡（DNN）反向傳播算法(BP)的，因為他寫的比我好多了，我就直接用他的了。

現在我們總結下DNN反向傳播算法的過程。由於梯度下降法有批量（Batch)，小批量(mini-Batch)，隨機三個變種, 為了簡化描述, 這裡我們以最基本的批量梯度下降法為例來描述反向傳播算法。實際上在業界使用最多的是mini-Batch的梯度下降法。不過區別又僅在於迭代時訓練樣本的選擇而已。

輸入: 總層數$L$, 以及各隱藏層與輸出層的神經元個數, 激活函數, 損失函數, 選代步長 $\alpha$,最大迭代次數$MAX$與停止迭代閾值$\epsilon$, 輸入的$m$個訓練樣本 $\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{m}, y_{m}\right)\right\}$。

輸出: 各隱藏層與輸出層的線性關係係數矩陣 $W$ 和偏倚向量$b$

初始化各隱藏層與輸出層的線性關係係數矩陣$W$和偏倚向量$b$的值為一個隨機值。
for iter to 1 to MAX:

2.1 for $i=1$ to $m$ :

a. 將DNN輸入 $a^{1}$ 設置為 $x_{i}$
b. for $l=2$ to $L,$ 進行前向傳播算法計算 $a^{i, l}=\sigma\left(z^{i, l}\right)=\sigma\left(W^{l} a^{i, l-1}+b^{l}\right)$
c. 通過損失函數計算輸出層的 $\delta^{i, L}$
d. for $l=$ L-1 to 2 , 進行反向傳播算法計算 $\delta^{i, l}=\left(W^{l+1}\right)^{T} \delta^{i, l+1} \odot \sigma^{\prime}\left(z^{i, l}\right)$
2.2 for $l=2$ to $\mathrm{L},$ 更新第$l$層的 $W^{l}, b^{l}:$

\[\begin{array}{c}
W^{l}=W^{l}-\alpha \sum_{i=1}^{m} \delta^{i, l}\left(a^{i, l-1}\right)^{T} \\
b^{l}=b^{l}-\alpha \sum_{i=1}^{m} \delta^{i, l}
\end{array}
\]

2-3. 如果所有$W,b$的變化值都小於停止迭代閾值 $\epsilon,$ 則跳出迭代循環到步驟3。

輸出各隱藏層與輸出層的線性關係係數矩陣$W$和偏倚向量$b$。

總結

這一篇博客主要是介紹了以下內容：

DNN介紹
DNN的基本結構
DNN的前向傳播
DNN的BP算法

本來是想在這一章博客中將CNN也介紹一下，但是想了想，可能還是分開介紹比較好。因此我將會在下一篇博客中主要會對CNN進行介紹以及部分推導。

參考

Tags: 數據挖掘