Kaggle竞赛入门(一):决策树算法的Python实现
- 2020 年 4 月 3 日
- 笔记
本文翻译自kaggle learn,也就是kaggle官方最快入门kaggle竞赛的教程,强调python编程实践和数学思想(而没有涉及数学细节),笔者在不影响算法和程序理解的基础上删除了一些不必要的废话,毕竟英文有的时候比较啰嗦。
一.决策树算法基本原理
背景:假设你的哥哥是一个投资房地产的大佬,投资地产赚了很多钱,你的哥哥准备和你合作,因为你拥有机器学习的知识可以帮助他预测房价。你去问你的哥哥他是如何预测房价的,他告诉你说他完全是依靠直觉,但是你经过调查研究发现他预测房价是根据房价以往的表现来进行预测的,作为一个机器学习编程者,正好也可以以往的房价进行未来房价的预测。机器学习当中有一个决策树的算法,可以用于未来房价的预测,这个模型是这样的,如下所示:
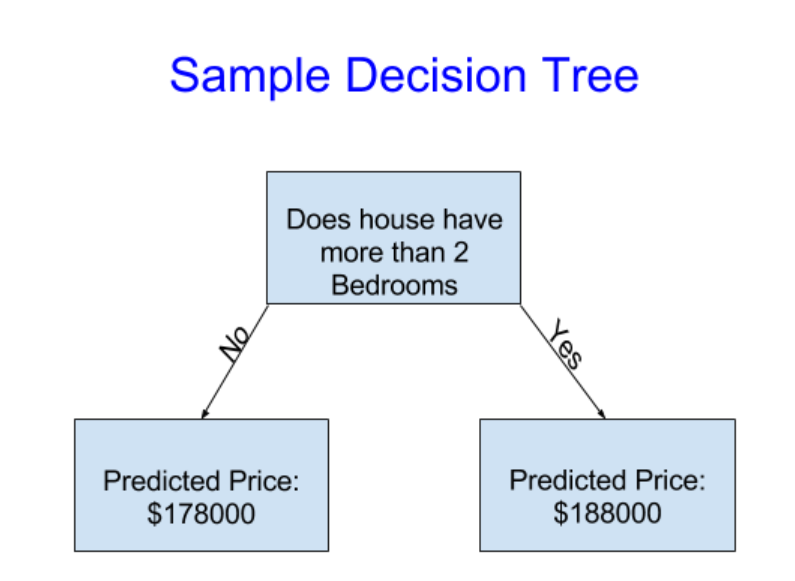
第一行的第一框表示程序的流程图:”如果房子里超过了2个卧室”则执行yes,不是的话则执行“No”,执行yes之后,我们就对它进行预测后的房价是188000刀,执行“no”之后的预测房价则是178000刀,这就是一个简单的决策树。一个条件只有是和否两个分支,但是能不能让这个模型更加合理一点呢?因此我们拟合出了第二个模型,如下图所示:
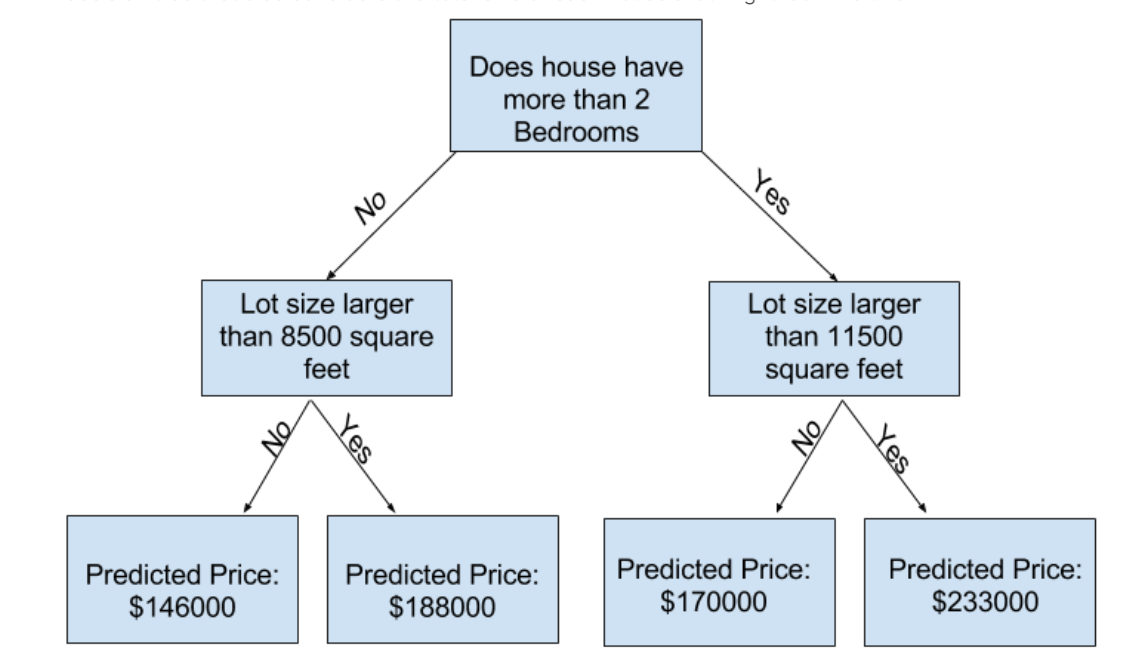
可以从中看到,除了考虑房子里拥有的房间数量,第二个statement(条件)还考虑到了房子的总面积是多大,接着再根据房间的总面积大小进行预测。得到预测的房价也就是prediccted price,我们将其命名为:“leaf”,中文也就是树叶的意思。这就是决策树算法的基本原理了!如果你想深挖其中的数学原理的话,我们将会在后面的章节当中讲解到。
二.使用Pandas来处理你的数据
pandas是Python程序里面的一个包,常常用于数据缺失值的处理和数据的清理,也用于导入数据。我们在Python当中导入这个包的代码如下:
import pandas as pd
在pandas当中最重要的部分就是DataFrame这个数据结构,这个数据结构将你导入的数据全部变成一张表的形式,学习过R语言的同学应该很清楚这是什么,没有学过的话你就把它当成一个类似EXCEL表格的东西就可以了,我们可以用pandas像EXCEL表格一样来处理数据。你使用pandas也是主要是使用DataFrame这个数据结构。假设你想要导入墨尔本的房价CSV数据到pandas当中,这个CSV文件的路径如下所示:
../input/melbourne-housing-snapshot/melb_data.csv
我们导入数据到pandas当中的代码如下:
# save filepath to variable for easier access melbourne_file_path = '../input/melbourne-housing-snapshot/melb_data.csv' # read the data and store data in DataFrame titled melbourne_data melbourne_data = pd.read_csv(melbourne_file_path) # print a summary of the data in Melbourne data melbourne_data.describe()
输出:
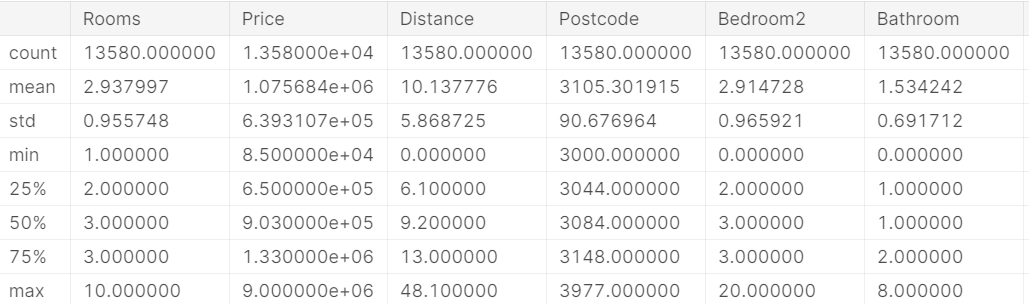
可以看到我们利用describe()函数将数据的各个属性输出得完完整整,包括数据出现的次数,平均值mean,标准差std,最小值min,最大值max,四分位数25%,75%。以及中位数50%。
三.为决策树模型选择数据
在一个数据集当中有大量的变量,如何才能够简化这些数据,让我们该选择哪些变量呢?
在这里我们暂时依靠直觉来选择变量,在我们后面的章节当中将会介绍统计学里的方法来选择这些变量。为了在pandas里面选择这些变量,我们需要选择一列一列的数据,而不是一行一行的数据,因为每一列代表一个不同的变量,比如price,rooms等,刚刚才已经使用descibe函数对这些变量进行展示了。我们来看看刚刚导入的墨尔本房产房产的数据一共有哪些变量,代码如下所示:
import pandas as pd melbourne_file_path = '../input/melbourne-housing-snapshot/melb_data.csv' melbourne_data = pd.read_csv(melbourne_file_path) melbourne_data.columns
输出:
Index(['Suburb', 'Address', 'Rooms', 'Type', 'Price', 'Method', 'SellerG', 'Date', 'Distance', 'Postcode', 'Bedroom2', 'Bathroom', 'Car', 'Landsize', 'BuildingArea', 'YearBuilt', 'CouncilArea', 'Lattitude', 'Longtitude', 'Regionname', 'Propertycount'], dtype='object')
在这个墨尔本房产数据集当中,有些数据已经缺失了,我们会在后面的章节当中介绍如何处理缺失数据,也就是进行数据的清理,现在我们进行下一步:
四.选择要进行预测的目标数据
很显然我们需要预测的是房价,在pandas当中,一个单列储存在一个数据结构:“Series”当中,就类似于DataFrame只有一列一样。我们将需要预测的变量命名为y,并将数据集里面的价格赋值给它,代码如下所示:
y = melbourne_data.Price
五.选择特征进行预测价格
我们仅选取几个特征进行数据的预测,代码如下:
melbourne_features = ['Rooms', 'Bathroom', 'Landsize', 'Lattitude', 'Longtitude']
在传统情况下,通常将这些数据命名为X,因为需要预测的值才是y,这样和统计学当中的x和y正好相对应,命名为x的代码如下:
X = melbourne_data[melbourne_features]
现在让我们用之前的describe()方法快速审计一下这些数据大概长什么样:
X.describe()
输出:
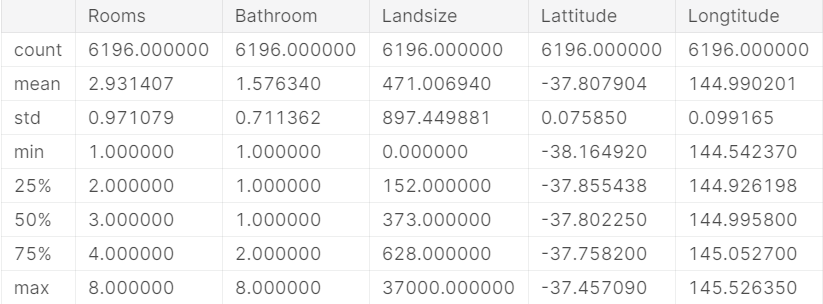
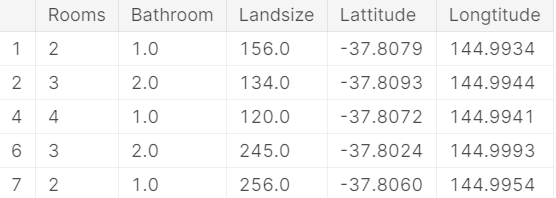
用head方法来查看前6行数据,和R语言的语法一模一样:
X.head()
输出:
六.拟合决策树模型
终于,数据准备完毕,我们来到了最激动人心的一步了!拟合决策树模型,在拟合决策树模型当中,我们会用到:scikit-learn 这个Python库,在拟合模型的时候我们需要如下这几步:
1.选择需要的是哪一个算法
2.模型的拟合(fit)
3.模型的预测(predict)
4模型的评估(Evaluate)
下面是我们拟合模型时所用到的代码,首先导包准备数据并选择决策树算法:
from sklearn.tree import DecisionTreeRegressor # Define model. Specify a number for random_state to ensure same results each run melbourne_model = DecisionTreeRegressor(random_state=1) # Fit model melbourne_model.fit(X, y)
输出:
DecisionTreeRegressor(criterion='mse', max_depth=None, max_features=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=1, min_samples_split=2, min_weight_fraction_leaf=0.0, presort=False, random_state=1, splitter='best')
现在我们的模型已经拟合完毕了,数据也已经全部完成了计算,我们一般情况下会使用除开我们数据集之外的房产的数据来预测房价,但我们这里为了看看模型拟合得是否好,就直接选取X当中的前五行数据,用预测数据和实际数据进行比对,代码如下:
print("Making predictions for the following 5 houses:") print(X.head()) print("The predictions are") print(melbourne_model.predict(X.head()))
输出的预测结果如下:
Making predictions for the following 5 houses: Rooms Bathroom Landsize Lattitude Longtitude 1 2 1.0 156.0 -37.8079 144.9934 2 3 2.0 134.0 -37.8093 144.9944 4 4 1.0 120.0 -37.8072 144.9941 6 3 2.0 245.0 -37.8024 144.9993 7 2 1.0 256.0 -37.8060 144.9954 The predictions are [1035000. 1465000. 1600000. 1876000. 1636000.]
这就是我们实现的第一个决策树算法模型啦!