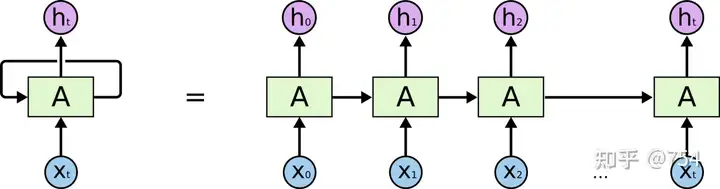
原始递归函数及模拟运行的优化
看到网上一个题目,证明x开y次方是原始递归函数(primitive recursive function)。这个问题并不难,只要把x开y次方实现出来即可。于是,正好把《递归论》相关内容补一补。
【原始递归函数】
首先,我们明确,《递归论》里研究的都是自然数里的函数。
所谓自然数,在这里的意思是指非负整数,我们可以用Peano五公理定义。
那么原题的x开y次方,x和y当然都是自然数,而且应该都是正整数,自然数下x开y次方的结果为实数下x开y次方得到的结果向下取整。当然,为了方便,x取0或者y取0的函数值可以随便定义。
在讲原始递归函数之前,我们先要定义几个基本函数,我们一般称之为本原函数:
零函数$z$,对于任何自然数,返回0。
后继函数$s$,对于任何自然数,返回它的后继数,也就是传入n返回n+1。
投影函数$p_k^i$,
$p_k^i(a_1,…a_n)=a_i$
以上,零函数和后继函数都是带一个元的函数,投影函数可以带任意多个元(当然,投影函数其实是一堆函数,而不是一个)。
但我们知道,我们平常遇到的自然数下的函数远远不止上面这么点,这就需要不断的用规则来合成新的函数,用于合成原始递归函数的规则有两个:
复合规则:
一个n元函数$f$和n个m元函数$g_0,…g_n$可以通过以下规则得到一个m元函数
$h(a_0,…a_m)=f(g_0(a_0,…a_m),…g_n(a_0,…a_m))$
递归规则:
一个n元函数$f$和一个n+2元函数$g$可以通过以下规则得到一个n+1元函数
$h(a_0,…a_n,0)=f(a_0,…a_n)$
$h(a_0,…a_n,t+1)=g(a_0,…a_n,t,h(a_0,…a_n,t))$
从本原函数开始出发,有限次通过上述规则所得到的函数,就叫原始递归函数了。当然,本原函数自己也是原始递归函数。
这个原始递归函数基本上覆盖了我们常见的几乎所有的自然数下的函数了。当然,既然有原始递归函数,就有一般递归函数了,函数产生规则多了个μ算子,不过这是本文叙述范围之外的事情。不过既然提到,说一下,一般认为,一般递归函数是可计算的,也就是图灵机可以解决的(可停机)。我们平常见到的绝大多数自然数下的函数都是原始递归函数。
【原始递归函数的可计算性】
原始递归函数的可计算性很容易证明。
首先,本原函数是可计算的。
然后,我们来看复合规则,如果$f$和$g_0,…g_n$都是可计算的,那么对于
$h(a_0,…a_m)=f(g_0(a_0,…a_m),…g_n(a_0,…a_m))$
$g_0(a_0,…a_m),…g_n(a_0,…a_m)$都是可计算的,
从而$f(g_0(a_0,…a_m),…g_n(a_0,…a_m))$是可计算的,
从而复合得到的函数$h$是可计算的。
最后,我们来看递归规则,如果$f$和$g$是可计算的,
那么
$h(a_0,…a_n,0)=f(a_0,…a_n)$是可计算的,
$h(a_0,…a_n,1)=g(a_0,…a_n,0,h(a_0,…a_n,0))$是可计算的
…
$h(a_0,…a_n,t+1)=g(a_0,…a_n,t,h(a_0,…a_n,t))$是可计算的
$h(a_0,…a_n,t+2)=g(a_0,…a_n,t+1,h(a_0,…a_n,t+1))$是可计算的
…
【实现】
我们就用Scheme来描述。
零函数z、后继函数s都很容易实现,
(define (z n) 0) (define (s n) (+ n 1))
而投影函数p则是一堆函数,于是使用p函数来产生投影函数
(define (p k i) (lambda s (list-ref s (- i 1)))))
两种函数产生规则可以看成是两个高阶函数,写起来并不复杂,毕竟这只是环境的基础,复杂的在后面
(define (comb g . h) (lambda s (apply g (map (lambda (f) (apply f s)) h)))) (define (primitive-rec g h) (lambda s (let ((rs (reverse s))) (let ((s2 (reverse (cdr s))) (n (car rs))) (if (zero? n) (apply g s2) (apply h (append s2 (list (- n 1) (apply (primitive-rec g h) (append s2 (list (- n 1))))))))))))
既然目的是为了写出开方,大致能想的出依次需要造出哪些函数,主方向上大致可以想到比如加法、比较、减法、乘法、乘方以及一些过程中的别的函数。
加法的定义可以这样:
$a+0=a$
$a+(n+1)=s(a+n)$
显然,这已经很像用递归规则可以写出的样子。
改一下上面的递推式,用符号$\oplus$来表示加法函数,
$add(a,0)=p_1^1(a)$
$add(a,n+1)=s(p_3^3(a,n,add(a,n)))$
为了区别+,我们在Scheme中用+~来表示加法,于是,很容易就写出代码
(define +~ (primitive-rec (p 1 1) (comb s (p 3 3))))
之后,我们Scheme里构造的函数都加上~来区别。
为了构造减法,我们想先构造一个后继函数的“相反”函数,前趋函数pre。
定义这个函数用在其他自然数上都是返回传入值减1,而对于0则返回0.
则定义如下:
$pre(0)=0$
$pre(n+1)=n$
这也很像用一次递归规则就可以完成的事,只可惜,无法构造出不带参数的函数,所以需要一个技巧,先构造一个带两元的函数。
$pre2(a,0)=0$
$pre2(a,n+1)=n$
那么也就是
$pre2(a,0)=z(a)$
$pre2(a,n+1)=p_3^2(a,n,pre2(a,n))$
再用pre2来通过复合规则构造pre函数。
(define pre~ (comb (primitive-rec z (p 3 2)) z (p 1 1)))
有了前趋函数,就可以构造减法。递归论的减法有一点不一样,在于a-b在a<b时等于0。
$sub(a,0)=a$
$sub(a,n+1)=pre(sub(a,n))$
于是
$sub(a,0)=p_1^1(a)$
$sub(a,n+1)=pre(p_3^3(a,n,sub(a,n)))$
写成代码如下:
(define -~ (primitive-rec (p 1 1) (comb pre~ (p 3 3))))
各种谓词肯定是需要的。
递归论里,我们一般用0、非0来代表假、真。
实现逻辑非和实现之前的pre函数的手法类似,我们先用递归规则做一个二元函数,然后再用复合规则。
(define not~ (comb (primitive-rec s (comb z (p 3 1))) z (p 1 1)))
我们可以很聪明的未必要用1来表示真,那么一切就很得心应手了。
与
$and(a,0)=0$
$and(a,n+1)=a$
或
$or(a,0)=a$
$or(a,n+1)=s(a)$ s是后继函数
异或
$xor(a,0)=a$
$xor(a,n+1)=not(a)$
以上都很容易看出我故意写成了递归规则这样,于是很容易写出代码
(define and~ (primitive-rec z (p 3 1))) (define or~ (primitive-rec (p 1 1) (comb s (p 3 1)))) (define xor~ (primitive-rec (p 1 1) (comb not~ (p 3 1))))
再写各种比较谓词,
大于等于
$ge(a,0)=s(a)$
$ge(a,n+1)=a-n$
大于
$gt(a,0)=a$
$gt(a,n+1)=a-s(n)$
小于
$lt(a,0)=0$
$lt(a,n+1)=s(n)-a$
以上依然用递归规则编写
(define >=~ (primitive-rec s (comb -~ (p 3 1) (p 3 2)))) (define >~ (primitive-rec (p 1 1) (comb -~ (p 3 1) (comb s (p 3 2))))) (define <~ (primitive-rec z (comb -~ (comb s (p 3 2)) (p 3 1))))
而小于等于可以用大于等于通过复合规则构造
$le(a,b)=gt(b,a)$
$=>$
$le(a,b)=gt(p_2^2(a,b),p_2^1(a,b))$
(define <=~ (comb >=~ (p 2 2) (p 2 1)))
也可以构造等于和不等于
$ne(a,b)=or(a-b,b-a)$
等于通过非和不等于两个谓词复合得到
$eq(a,b)=not(ne(a,b))$
(define !=~ (comb or~ -~ (comb -~ (p 2 2) (p 2 1)))) (define =~ (comb not~ !=~))
以上这些谓词对于我们最终的开方来说,大多是不需要的。
乘法是很容易用递归规则实现的
$mul(a,0)=0$
$mul(a,n+1)=add(a,mul(a,n))$
(define *~ (primitive-rec z (comb + (p 3 1) (p 3 3))))
有了乘法,乘方也一样(我们不考虑0为底)
$pow(a,0)=1$
$pow(a,n+1)=mul(a,pow(a,n))$
(define pow (primitive-rec (comb s z) (comb * (p 3 1) (p 3 3))))
最后,我们就可以构造开方了。想到的构造开方的方式有很多种,以下选择一种,
我们取$root(0,n)=0$
根据
$root(m+1,n)\le root(m,n)+1$
将$root$函数的两个参数交换为$rootv$
可以用递归规则来构造$rootv$,
$rootv(a,0)=0$
$rootv(a,n+1)=if\ {(rootv(a,n)+1)}^{a} \le n+1\ then\ rootv(a,n)+1\ else\ rootv(a,n)$
我们给if-else做个函数,叫condch
$condch(a,b,0)=b$
$condch(a,b,n+1)=a$ 此时第三个参数为非0
(define condch~ (primitive-rec (p 2 2) (p 4 1)))
于是,重新整理$rootv$
$rootv(a,0)=z(a)$
$rootv(a,n+1)=condch(s(rootv(a,n)),rootv(a,n),le(expt(s(rootv(a,n))),s(n)))$
再交换一下两个参数,当然用的是复合规则,得到$root$函数
写成代码
(define root~ (comb (primitive-rec z (comb condch~ (comb s (p 3 3)) (p 3 3) (comb <=~ (comb pow~ (comb s (p 3 3)) (p 3 1)) (comb s (p 3 2))))) (p 2 2) (p 2 1)))
到这里为止,我们已经用原始递归函数的构造方式实现了开方,当然证明了开方运算是原始递归函数。
再拿程序测试了几下,数比较小的时候,结果都是对的,数稍微大一点计算量很大就算了。
【优化】
以上的运算效率很慢,一个原因在于运算方式。
比如投影函数,虽然是从几个数中选择一个,明明对于纯函数来说,不选择的几个数去计算是多余的,但基于Lisp的运算规则限制,这是必须要先算的。
递归规则中,也会带来相同的问题。
以上问题导致了绝大部分的无意义计算,从而使得运算速度非常缓慢。
一种思路是运算的时候再加个call函数,按之前,z、s、p、comb、primitive-rec都为产生函数的实现下,call函数应该如下:
(define (call f . s) (apply f s))
而此处,加了一个call就给了优化无限的可能。我们可以换一条思路来实现上面的z、s、p、comb、primitive-rec,引入优化,比如z、s、p、comb、primitive-rec拼成数据结构来代表计算。
(define z 'z) (define s 's) (define p (lambda (k i) `(p ,k ,i))) (define (comb . fs) `(comb ,@fs)) (define (primitive-rec g h) `(rec ,g ,h)
比如之前的(define +~ (primitive-rec (p 1 1) (comb s (p 3 3))))
+~就是list结构,(rec (p 1 1) (comb s (p 3 3)))
然后call函数再来对这样的list来进行优化,产生较高效的计算方式。
我这里是再call函数里先将上述的list转换成lambda表达式,然后再对lambda表达式进行优化。
(define (call f . s) (apply (eval (func->lambda f)) s))
这里的func->lambda则是包含了转换为lambda表达式以及对lambda表达式的优化。优化一般以pass的方式,依次进行,每个pass只做一件事情。循环进行,到无法改变代码的时候结束。
(define (optimize s)
(let ((passes (list
;...all optimization passes
)))
(do
((r s (fold-left
(lambda (r pass)
(pass r))
r
passes))
(r-old '() r))
((equal? r-old r)
r))))
本想写出Knuth’s up arrow的表示的(虽然计算就不指望了),带三个参数,
用 k(a, b, c)来代表
a ↑…↑ b
箭头个数为c
但感觉写不出,怀疑它不是原始递归函数,可惜不会证明,哪位大佬看到给个证明吧。
源码放在github里,点击下面图片