浅谈树模型与集成学习-从决策树到GBDT
- 2021 年 7 月 30 日
- 笔记
引言
神经网络模型，特别是深度神经网络模型，自AlexNet在Imagenet Challenge 2012上的一鸣惊人，无疑是Machine Learning Research上最靓的仔，各种进展和突破层出不穷，科学家工程师人人都爱它。
机器学习研究发展至今，除了神经网络模型这种方法路径外，还存在许多大相径庭的方法路径，比如说贝叶斯算法、遗传算法、支持向量机等，这些经典算法在许多场景上也一直沿用。本文介绍的树模型，也是一种非常经典的机器学习算法，在推荐系统上经常能看到它的身影。
那这个树模型是怎样构建和实现的，其核心idea是什么？树模型效果不够好，又可以用什么样的思路和办法改进呢？本文主要包含以下三个方面的内容：
1.决策树
2.集成学习
3.随机森林与梯度提升决策树
决策树
决策树(Decision Tree)是树模型中最简单的一个模型，也是后面将要介绍到的随机深林与梯度提升决策树两个模型的基础。利用决策树算法，在历史约会数据集上，我们可以画出这样一个树，这颗树上的叶子节点表示结论，非叶子节点表示依据。一个样本根据自身特征，从根节点开始，根据不同依据决策，拆分成子节点，直到只包含一种类别(即一种结论)的叶子节点为止。
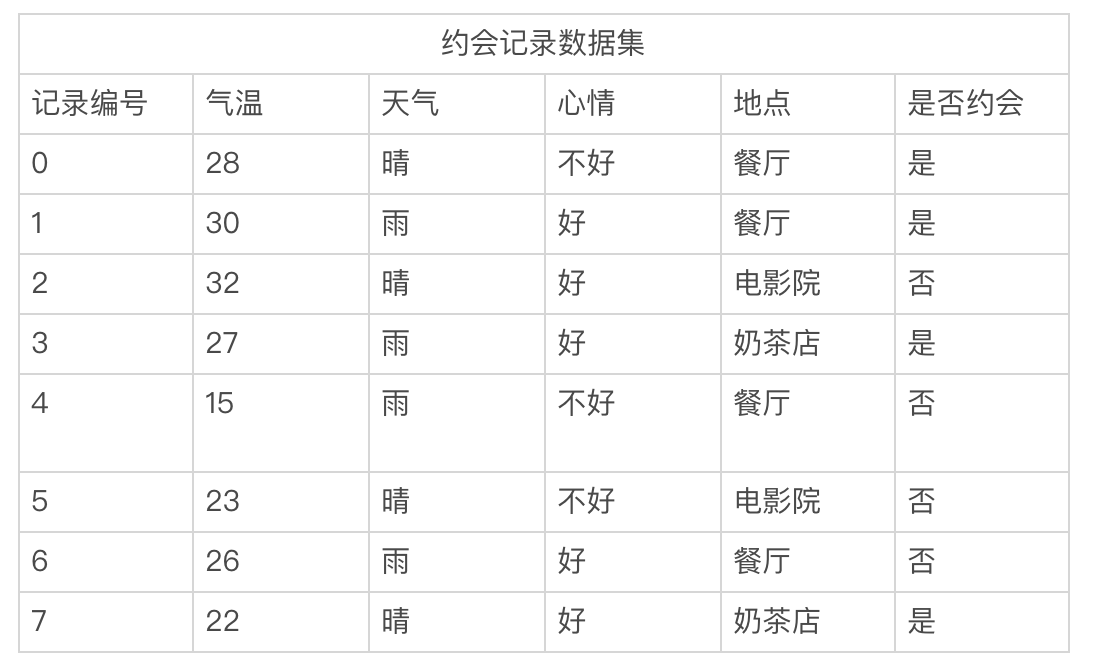
假设有如上面表格的一个数据集，基于这样数据可以构建成这样的一颗决策树，如下图所示。
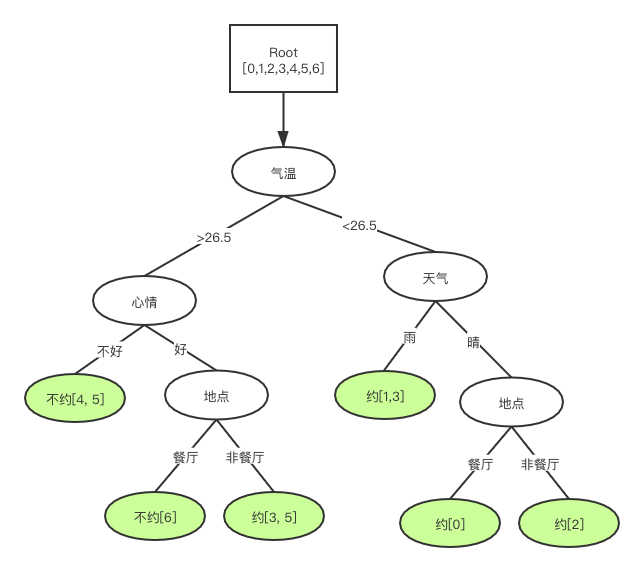
信息熵与基尼不纯度
可以看出构建决策树的关键是”分裂”，不断地分裂成子节点，一直到叶子节点(不能分裂)为止。那么这个关键分裂的标准和方法是什么、怎么分才是最好最恰当的呢？显然，能把正负样本完全划分开，一边正一边负，两边集合都是很“确定的”最好。在这里确定性是指一个事件只出现一个结果的可能性，那如何量化“确定性”这个指标呢，一般有两种方法：信息熵和基尼不纯度。
信息熵Entropy，是用来衡量信息的不确定性的指标，其计算方式如下：
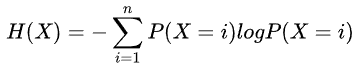
其中P(X=i)为随机变量X取值为i的概率。
基尼不纯度，实际上是对信息熵的一种近似的简化计算，因为对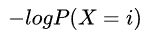
进行泰勒展开后，由于
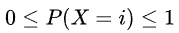，所以高阶项近似为0可忽略，仅保留一阶项1-P(X=i)
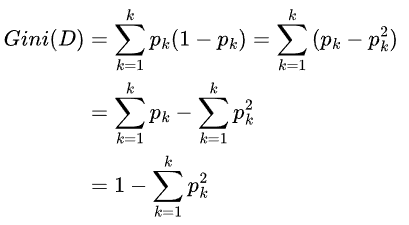
其中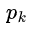
表示选中样本为第k类的概率。从公式上看，基尼不纯度可理解为，从数据集D中随机抽取两个样本，这两个样本刚好不同类的概率。
信息熵和基尼不纯度都能客观而具体地量化出“不确定性”，这两个指标越大反映事物不确定性的程度越高。
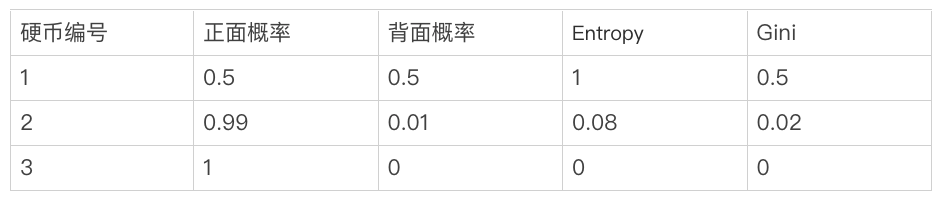
比如有三个硬币，第一个硬币其正背面质量完全均衡，抛出正背面概率相同，第二个硬币正面质量大于背面，其抛出正面概率远大于背面，第三个硬币则一定会抛出正面。这三个硬币里面，第三个硬币的不确定性的程度最低，因为其没有任何的不确定性，抛出正面是个必然事件；第一个硬币不确定性的程度最高，没办法确定抛出的正面还是背面；第二个硬币不确定性程度次之，因为其有比较大概率是能抛出正面，能相对确定一些。
构建分类树
有了对”不确定性”的量化方法，我们利用这些指标，来指导我们应该选择那个特征、特征怎么分叉，保证每一步“分裂”都是最优的，一直迭代到叶子节点为止。显然这个决策树的构建算法就是个贪心算法。考虑到算法实现的问题，这个决策树最好是二叉的而不是多叉，所以我们一般用二叉的CART(Classification And Regression Tree)算法构建决策树。
以约会数据集D为例，Gini(D) = 0.5，划分成两个集合d1, d2，标签0和1表示否和是。基尼增益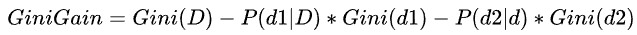
，如下表格所示我们利用基尼增益选特征，并确认其最佳分叉点。
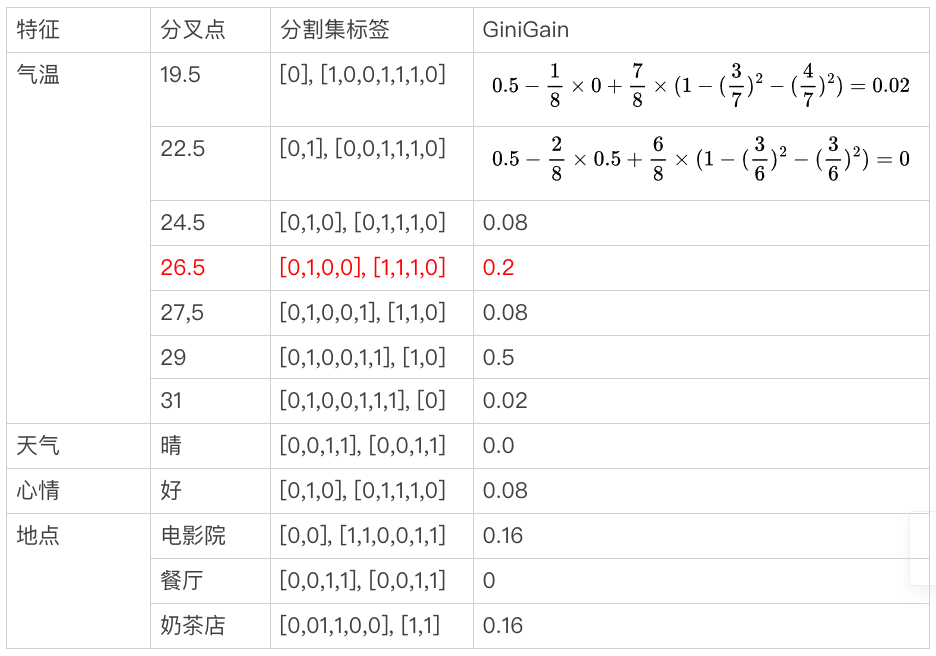
可见，基于气温特征在分叉点为26.5的情况下，将数据集D划分成<d1, d2>两个集合，其获得基尼增益最大。重复这个步骤，将d1和d2继续拆分下去，直到集合无法再分，或基尼增益小于或等于0为止。
构建回归树
决策树用于回归问题，思路与用分类问题的思路是一样的。只是将分裂好坏的评价方法，又信息熵改成平方误差函数，也就是把增益函数改成平方误差增益即可。
假设训练集中第j个特征变量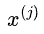
和它的取值s，作为切分变量和切分点，并定义两个区域
、
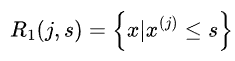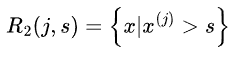为找出最优的j和s，对下式求解
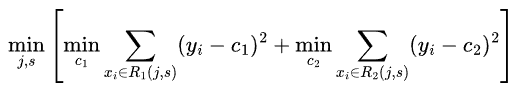
提高树模型的性能
在构建决策树的过程中，我们能看到只要样本不冲突(样本既是正样本，又是负样本)，是一定能收敛的，代价就是在决策树上添加更多（覆盖样本少的）叶子节点。但是这样的决策树，是完全没用归纳总结数据的规律，只是相当于把训练集用树的形式给背了下来，对于未训练的数据样本可能完全不是一回事，这学到的模型实际上是没有意义的。
决策树比较容易过拟合，因此需要树的结构进行约束。利用剪枝等方法来砍掉冗余的分支，使得树结构尽量简单，以提高树模型在未训练数据上的预测表现(也就是泛化能力)。除此之外，集成学习(Ensemble Learning)，横向地增加多个树，并利用多个树模型结果综合判断，也是个能提高模型性能常用方法。经常用在机器学习领域上的各种比赛和竞赛上，是个经典的刷榜套路。
集成学习
我们知道模型都不是完美的，而是有误差的。而模型的误差可以分成两种，一种是偏差(Bias)可理解为与模型预测均值与样本真值的误差，一种是方差(Variance)可理解为模型预测值自身的变化幅度。下图形象地了描述这两个概念。
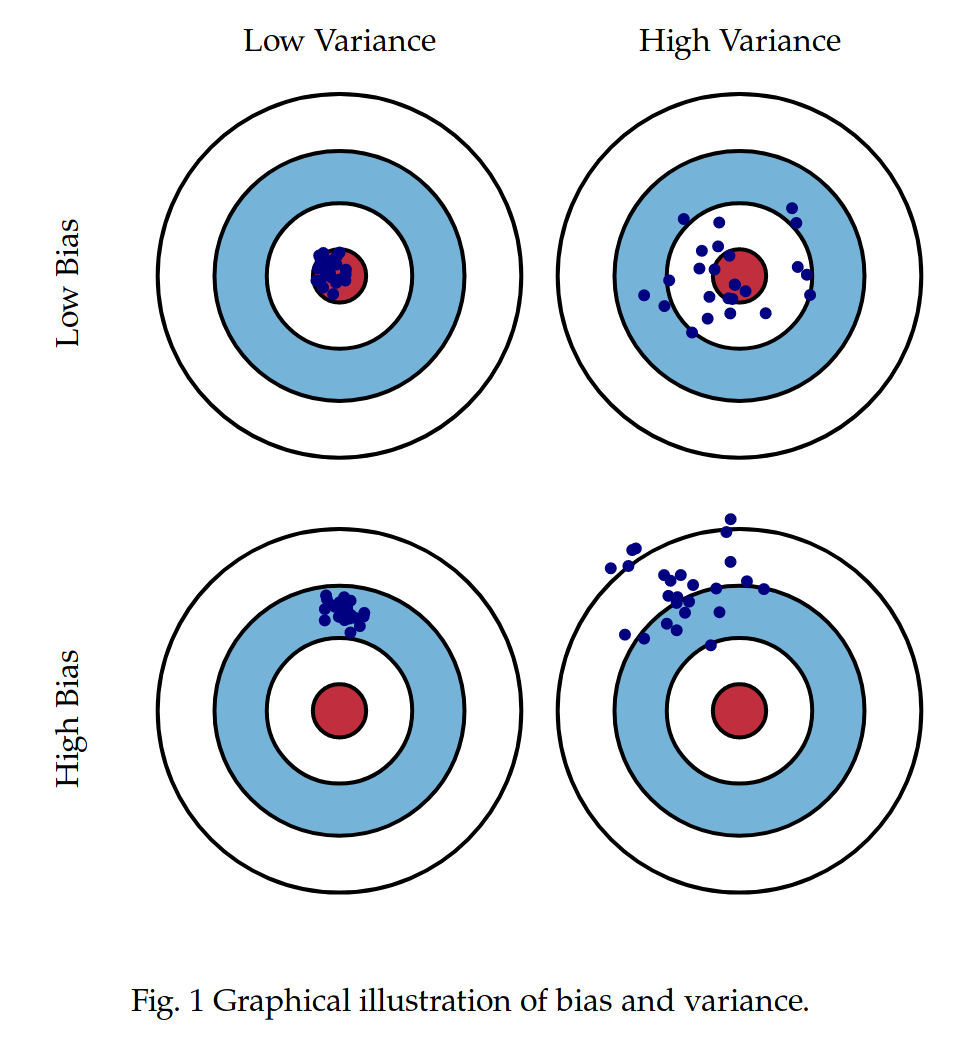
集成学习算法思考的问题就是：多个误差大效果差的个体模型，能不能以某种形式集成起来，变成一个误差变小效果变好的总体模型呢？这个答案肯定是显然的，我们都知道人民群众力量大。其背后的思想就是即使有个别模型预测错误，那么还有其他模型可以纠正回来，正所谓三个臭皮匠胜过一个诸葛亮。
从集成形式上看，主要可以分成两类，一类模型并行集成的bagging方法，一类模型串行集成的boosting方法。至于为什么能通过这样形式的集成就能提性能，其理论依据是什么？这可由模型总体期望和方差，与个体模型方差和偏差之间关系，得出严格的数学推导和证明，这里就不展开了。
随机森林
随机森林(Random Forrest)，一个基于bagging方法，把多个决策树集成到一起的模型算法。其核心的算法思想就是，通过多个(低偏差高方差)个体模型的均值，来方式降低总体方差的学习方法。随机森林算法框架如下图所示。
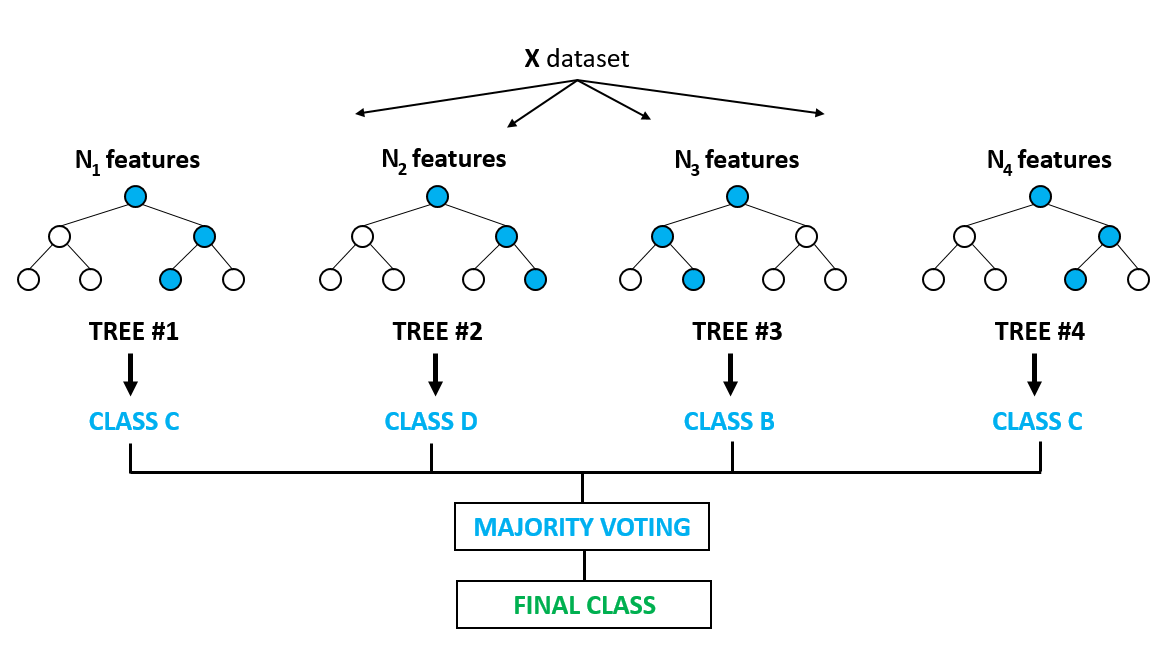
随机森林构建流程如下:
1. 把原始集上随机只采样N份样本数据集，且每份样本数据集随机只采样M个特征，得到若干份数据集
2. 在每个数据集上独立构建一颗决策树，得到N颗决策树
随机森林使用流程如下:
1. 把待预测的样本数据，输入到N个决策数，得到N个预测结果
2. 对这些预测结果，以投票(分类)或平均(回归)的计算方式最终结果
可见，在随机森林里面，每一颗决策树的构建(训练)都独立的，他们之间是并行的没有依赖。只是在最后使用(预测)时，要把森林上所有树的结果都过一遍，通过大家投票或平均的方式给出一个final decision。
梯度提升决策树
简称GBDT(Gradient Boosting Decision Tree)，一个基于boosting把多颗决策树串联集成一起训练学习的算法，其核心的算法思想是基于残差的学习，通过多个(低方差高偏差的)个体模型的叠加求和，来降低总体偏差的学习方法。
假设样本X的真值为30，模型1预测结果与真值的残差为10。为了修补这个残差，需要把样本X再送到模型2，但此时模型2训练的目标，并不是样本本身的真值30，而是当前的残差10。此时模型1和模型2相加后，残差已经从10减小4了。以相同的方式再训练模型3和模型4，总体的残差会越来越小，总体结果就是所有模型输出相加之和，如下为GBDT的训练过程示意图。
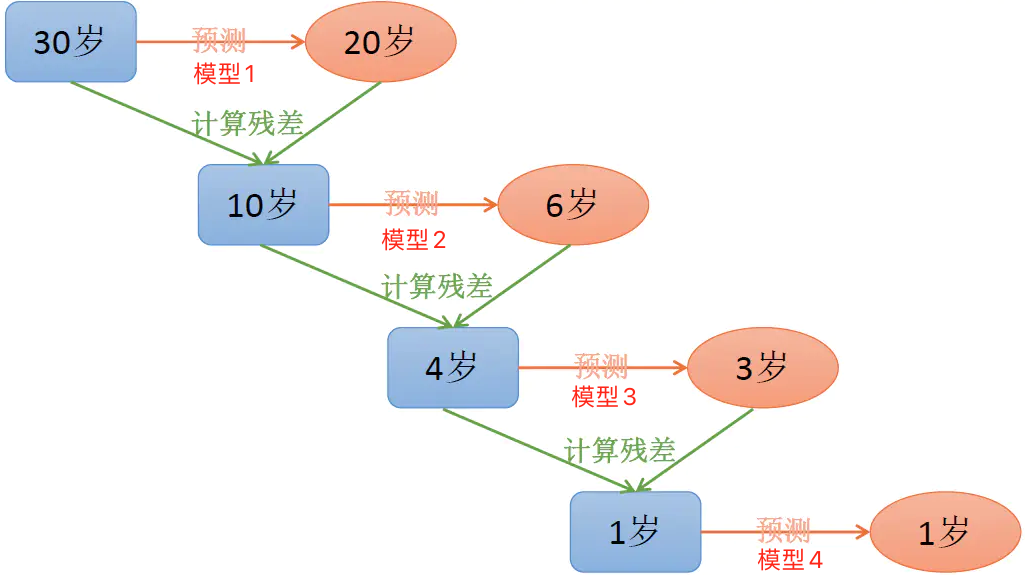
可见，这与bagging的随机森林方法完全不一样。前者模型之间相互独立，只要把子模型一一单独训练完就好了。而后者模型前后之间有依赖的关系，必须是练好上一颗树好后，根据残差再练下一颗，one by one的方式来训练。那如何实现这样的学习算法呢？GBDT就是这样的学习算法，其框架图如下：
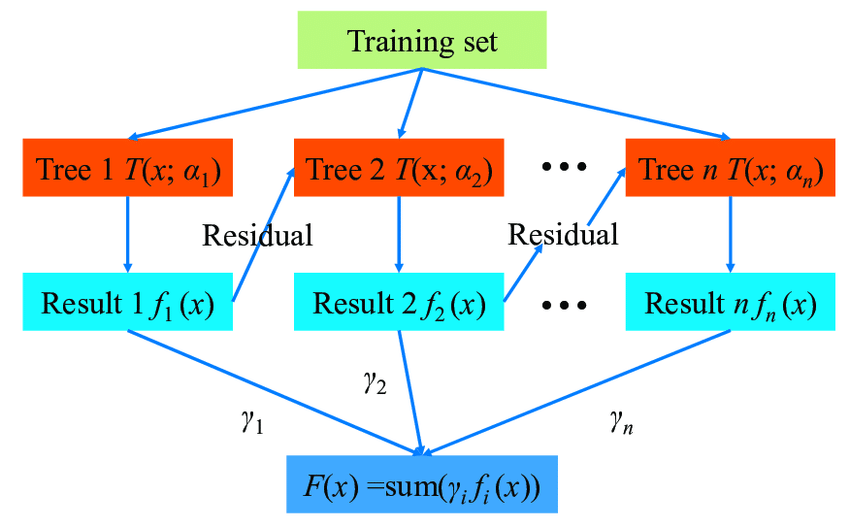
目标函数构建
我们知道对于逻辑回归模型的学习问题，其优化目标就是最小化交叉熵(CrossEntropy)损失函数：
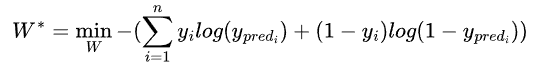
由于这函数是个凸函数的，所以这个最小值的求解问题比较简单。只要通过梯度下降法，迭代参数W逼近极值，就能使得交叉熵损失函数取到最小值。那么对于boosting这样加法模型的学习问题，其优化目标或者说损失函数，这个函数应该是长什么样子的，又是如何构建的呢？
要确定损失函数，首先第一步得确定模型是怎么输出预测值的。假定有已经训练了K颗树，则对于第i个样本的当前预测值为：
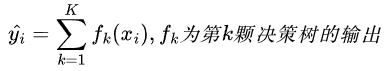
那么目标函数则就可以这样构建：
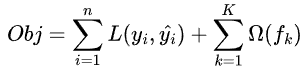
表达式右边的为正则项，用来控制模型结构的复杂程度，在决策树模型中，常用树的叶节点数量、叶子节点的值、以及树的深度来定义之。重点来关注左边的损失函数，应该怎么求解其最小值呢。进一步拆解损失函数，实现损失函数参数化：假定现有K颗树，前面的K-1颗树已经训练好，当前需要训练第K颗树。对于输入样本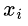
，如下图所示：
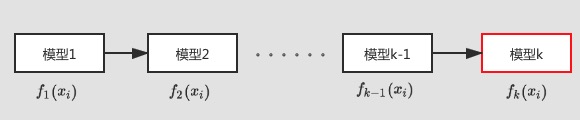
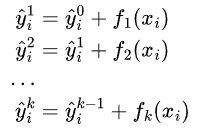
则目标函数可简化为
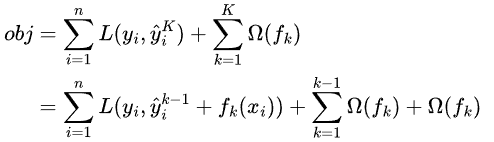
当训练第K颗树时，前K-1颗树已经确定下来，所以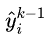
可作常数看待，
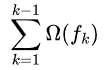与第K颗树无关，故此时目标函数为：
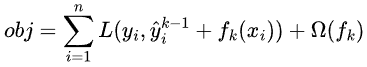
目标函数仍难以优化，利用泰勒级数来近似
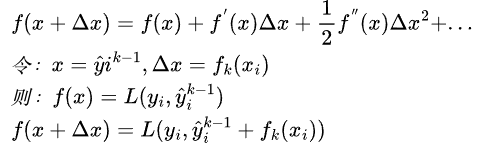
泰勒展开只保留前二阶，此时目标函数可写成：
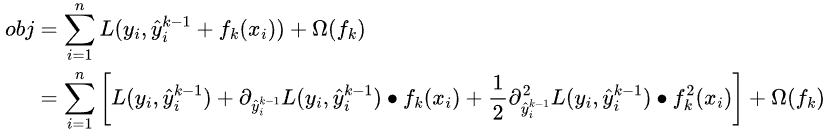
现在最优化的目标参数是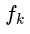
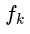，所以与无关的项都可以去掉。令
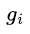和
为
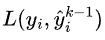关于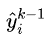
的一二阶导数，因为前K-1颗树已训练，所以这两个值可算出，可认为是已知的。
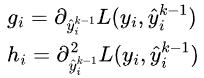
故目标函数再简化为:
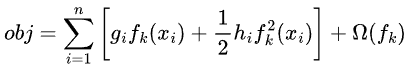
最优化树参数的求解
决策树的输出函数f的，可以这样定义：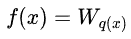
，其中q(x)是位置函数，表示样本x会落到树的那个位置(第几个叶子节点)，
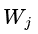表示第j个叶子的值。而树结构约束函数
，与叶子的值W和叶子的个数T有关，分别由两个超参数来控制：
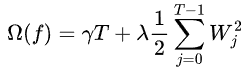
故此时目标函数再简化为：
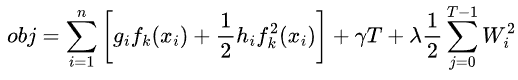
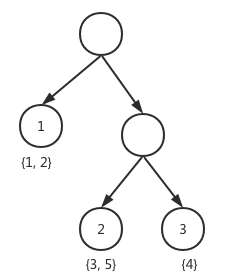
在树形态确定情形下，遍历样本组织形式，可叶子上样本集合划分，逐个集合形式来遍历，比如下图先叶子节点1上的{1,2}样本，再叶子接上2上{3,5}，如下图：
表示叶子节点j上的样本集合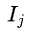
，
则的目标函数写成下形式为：
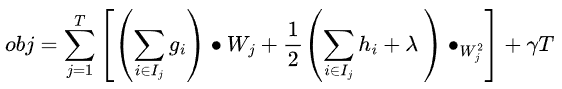
再令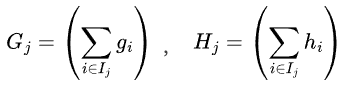
，在树形状确定已知时，这两个都是常数。此时就只剩下W一个参数了，而此时的目标函数就成了一个最简单的一元二次函数，这个函数极值点可以直接用通解公式就可以算出来。
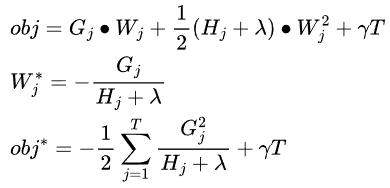
最优化树形态的求解
训练数据有限，而树的形态是无限的。有无限多种形态的树，都能把这些训练放入到其叶子节点上。在这里寻找一个最优的，其实就是个典型NP-hard问题，很难直接优化。而且树的形态，也很难定义成一个连续的函数，没有条件用梯度下降来求解。那么如何求解之？跟决策树的构建算法一样，沿用贪心算法思路，遍历所有特征，找当前最优的特征划分方法F，确定最优树形态。
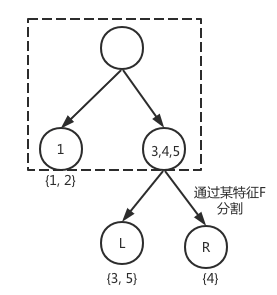
如上图，假定当前已经决策树已经分成了两个叶子点(框线内)，此时应该不应该通过特征F继续分裂，选择那种划分方式最好？
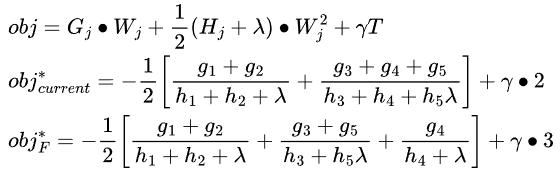
故通过特征划分方法F所形成的树形，使得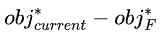
最大化，就是当前最优的树形状。为了算法实现的便利，我们限制了特征划分的形式，对于每一步叶子节点划分操作，都只能分裂左右两个叶子节点，以确保树是二叉的。所以最终有：
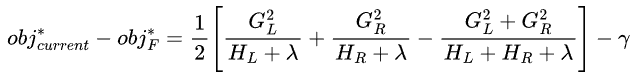
引用
XGBoost：A Scalable Tree Boosting System. KDD 2016 ChenTianqi
【机器学习】决策树（中）//zhuanlan.zhihu.com/p/86263786
欢迎关注凹凸实验室博客：aotu.io
或者关注凹凸实验室公众号（AOTULabs），不定时推送文章：
