jzoj 6798. 【2014广州市选day2】regions
Description
在平面上堆叠着若干矩形,这些矩形的四边与平面X坐标轴或Y坐标轴平行。下图展示了其中一种情况,3个矩形的边将平面划分成8个区域:
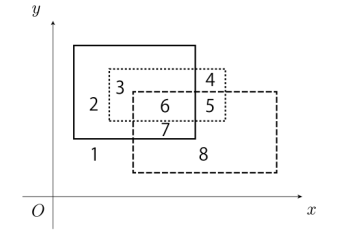
下面展示了另一种稍稍复杂一些的情况:
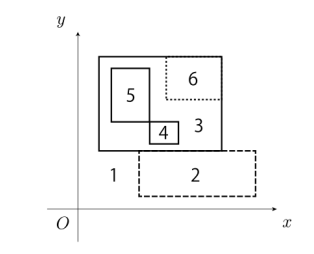
你的任务是写一个程序,判断这些矩形将平面分成了几个区域。
Input
输入的第一行是一个正整数n(n<=50),分别矩形的数目,接下来的n行,每行有4个用空格分隔的整数li,ti,ri,bi(1<=i<=n)代表了第i个矩形的坐标,(li,ti)代表该矩形左上角的X坐标和Y坐标,(ri,bi)代表该矩形右下角的X坐标和Y坐标,0<=li<ri<=\(10^{6}\),0<=bi<ti<=\(10^{6}\))
Output
输出只有一个整数,代表这些矩形将平面划分成多少区域。
Solution
这道题有两个做法。
首先先将横坐标纵坐标离散化。
第一个做法:
用并查集,将相连的块连接起来,最后查有多少个块
第二个做法:
将边打上标记,将没被打标记的点进行扩散,统计块数
(作者用的是第一个做法)
Code
#include <cstdio>
#include <algorithm>
#define open(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout);
using namespace std;
int i,p,last,fa[500001],n,j,heng,shu,l,r,ans,u,v,bj[500001];
bool bz[1001][1001];
struct re{
int x1,x2,y1,y2;
}a[51];
struct node{
int a,pl;
}k[100001];
const int d[5][2]={{0,0},{-1,0},{1,0},{0,1},{0,-1}};
bool cmp(node x,node y){return x.a<y.a;}
bool rec(node x,node y){return (x.pl<y.pl)||(x.pl==y.pl && x.a<y.a);}
int gf(int x)
{
if (x==fa[x]) return x;
fa[x]=gf(fa[x]);
return fa[x];
}
void ls()
{
sort(k+1,k+2*n+1,cmp);
p=0,last=0;
for (i=1;i<=n+n;i++)
{
if (k[i].a==k[i-1].a) k[i-1].a=last;else
{
k[i-1].a=last;
last=++p;
}
}
k[n+n].a=last;
sort(k+1,k+2*n+1,rec);
}
int main()
{
open("regions");
scanf("%d",&n);
for (i=1;i<=n;i++)
{
scanf("%d%d%d%d",&a[i].x1,&a[i].y1,&a[i].x2,&a[i].y2);
k[i].a=a[i].x1;k[i+n].a=a[i].x2;
k[i].pl=k[i+n].pl=i;
}
ls();
heng=p*2;
for (i=1;i<=n;i++)
{
a[i].x1=k[2*i-1].a*2;a[i].x2=k[2*i].a*2;
}
for (i=1;i<=n;i++)
{
k[i].a=a[i].y1;k[i+n].a=a[i].y2;
k[i].pl=k[i+n].pl=i;
}
ls();
shu=p*2;
for (i=1;i<=n;i++)
{
a[i].y1=k[2*i-1].a*2;a[i].y2=k[2*i].a*2;
}
for (i=1;i<=n;i++)
{
l=a[i].x1;r=a[i].x2;
for (j=a[i].y1;j<=a[i].y2;j++)
bz[l][j]=bz[r][j]=1;
l=a[i].y1;r=a[i].y2;
for (j=a[i].x1;j<=a[i].x2;j++)
bz[j][l]=bz[j][r]=1;
}
for (i=0;i<=heng;i++)
{
for (j=0;j<=shu;j++)
fa[i*shu+j]=i*shu+j;
}
for (i=0;i<=heng;i++)
{
for (j=0;j<=shu;j++)
{
if (bz[i][j]) continue;
for (l=1;l<=4;l++)
{
if (i+d[l][0]<=heng && i+d[l][0]>=0 && j+d[l][1]<=shu && j+d[l][1]>=0)
{
if (!bz[i+d[l][0]][j+d[l][1]])
{
u=gf(i*shu+j);
v=gf((i+d[l][0])*shu+j+d[l][1]);
if(fa[v]!=u) fa[u]=v;
}
}
}
}
}
for (i=0;i<=heng;i++)
{
for (j=0;j<=shu;j++)
{
if (bz[i][j]) continue;
u=gf(i*shu+j);
if (!i || !j || i==heng || j==shu)
{
if (!bj[u])bj[u]=2;
if (bj[u]==1) bj[u]=2,ans--;
}
if (!bj[u])
{
bj[u]=1;
ans++;
}
}
}
printf("%d",ans+1);
return 0;
}


