归并排序——C语言
- 2019 年 10 月 3 日
- 筆記
归并排序
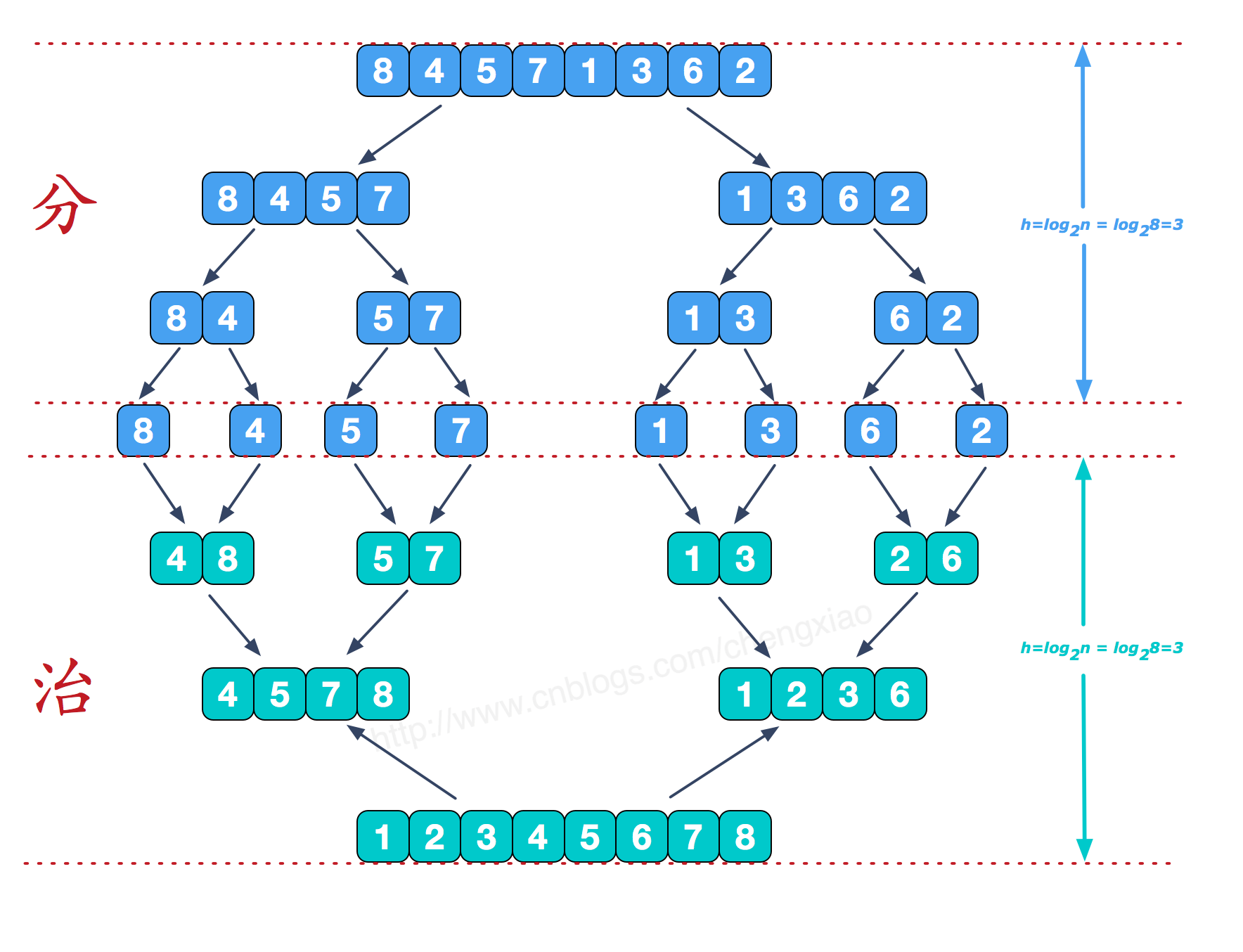
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案”修补”在一起，即分而治之)，将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序，若将两个有序表合并成一个有序表，称为二路归并
1、归并排序的基本思想
将待排序序列R[0…n-1]看成是n个长度为1的有序序列，将相邻的有序表成对归并，得到n/2个长度为2的有序表；将这些有序序列再次归并，得到n/4个长度为4的有序序列；如此反复进行下去，最后得到一个长度为n的有序序列
2、归并排序的算法描述
第一步：申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
第二步：设定两个指针，最初位置分别为两个已经排序序列的起始位置
第三步：比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
重复步骤3直到某一指针超出序列尾，将另一序列剩下的所有元素直接复制到合并序列尾
归并排序其实要做两件事：
（1）“分解”——将序列每次折半划分（递归实现）
（2）“合并”——将划分后的序列段两两合并后排序
如何合并？
在每次合并过程中，都是对两个有序的序列段进行合并，然后排序。
这两个有序序列段分别为 R[low, mid] 和 R[mid+1, high]。
先将他们合并到一个局部的暂存数组R2中，带合并完成后再将R2复制回R中。
我们称 R[low, mid] 第一段，R[mid+1, high] 为第二段。
每次从两个段中取出一个记录进行关键字的比较，将较小者放入R2中，最后将各段中余下的部分直接复制到R2中。
经过这样的过程，R2已经是一个有序的序列，再将其复制回R中，一次合并排序就完成了。
3、代码实现
1 /* 将序列对半拆分直到序列长度为1*/ 2 void MergeSort_UptoDown(int *num, int start, int end) 3 { 4 int mid = start + (end - start) / 2; 5 6 if (start >= end) 7 { 8 return; 9 } 10 11 MergeSort_UptoDown(num, start, mid); 12 MergeSort_UptoDown(num, mid + 1, end); 13 14 Merge(num, start, mid, end); 15 } 16 17 void Merge(int *num, int start, int mid, int end) 18 { 19 int *temp = (int *)malloc((end-start+1) * sizeof(int)); //申请空间来存放两个有序区归并后的临时区域 20 int i = start; 21 int j = mid + 1; 22 int k = 0; 23 24 while (i <= mid && j <= end) 25 { 26 if (num[i] <= num[j]) 27 { 28 temp[k++] = num[i++]; 29 } 30 else 31 { 32 temp[k++] = num[j++]; 33 } 34 } 35 36 while (i <= mid) 37 { 38 temp[k++] = num[i++]; 39 } 40 while (j <= end) 41 { 42 temp[k++] = num[j++]; 43 } 44 45 //将临时区域中排序后的元素，整合到原数组中 46 for (i = 0; i < k; i++) 47 { 48 num[start + i] = temp[i]; 49 } 50 51 free(temp); 52 }
4、拆分过程
（图片来源：https://www.cnblogs.com/chengxiao/p/6194356.html）
完整代码：
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 void MergeSort_UptoDown(int *num, int start, int end); 5 void Merge(int *num, int start, int mid, int end); 6 7 int main() 8 { 9 /* 归并排序（升序） */ 10 int num[10] = {5, 1, 8, 4, 7, 2, 3, 9, 0, 6}; 11 int length = sizeof(num) / sizeof(num[0]); 12 int i; 13 14 MergeSort_UptoDown(num, 0, length - 1); 15 16 for (i = 0; i < length; i++) 17 { 18 printf("%d ", num[i]); 19 } 20 21 return 0; 22 } 23 24 /* 将序列对半拆分直到序列长度为1*/ 25 void MergeSort_UptoDown(int *num, int start, int end) 26 { 27 int mid = start + (end - start) / 2; 28 29 if (start >= end) 30 { 31 return; 32 } 33 34 MergeSort_UptoDown(num, start, mid); 35 MergeSort_UptoDown(num, mid + 1, end); 36 37 Merge(num, start, mid, end); 38 } 39 40 void Merge(int *num, int start, int mid, int end) 41 { 42 int *temp = (int *)malloc((end-start+1) * sizeof(int)); //申请空间来存放两个有序区归并后的临时区域 43 int i = start; 44 int j = mid + 1; 45 int k = 0; 46 47 while (i <= mid && j <= end) 48 { 49 if (num[i] <= num[j]) 50 { 51 temp[k++] = num[i++]; 52 } 53 else 54 { 55 temp[k++] = num[j++]; 56 } 57 } 58 59 while (i <= mid) 60 { 61 temp[k++] = num[i++]; 62 } 63 while (j <= end) 64 { 65 temp[k++] = num[j++]; 66 } 67 68 //将临时区域中排序后的元素，整合到原数组中 69 for (i = 0; i < k; i++) 70 { 71 num[start + i] = temp[i]; 72 } 73 74 free(temp); 75 }
View Code
