算法修炼之路——【链表】Leetcode24 两两交换链表中的节点
- 2020 年 4 月 4 日
- 筆記
题目描述
给定一单链表,两两交换其中相邻的节点,并返回交换后的链表。
你不能只是简单的改变节点内部的值,而是需要实际的进行节点交换。
示例:
输入:head = [1, 2, 3, 4]
输出:head = [2, 1, 4, 3]
解题思路
我们通过示例可以简单了解到,需要两两进行位置互换,但是互换的动作需要涉及到前置节点与后置节点。这里为方便理解,我们先单独给出四个节点:
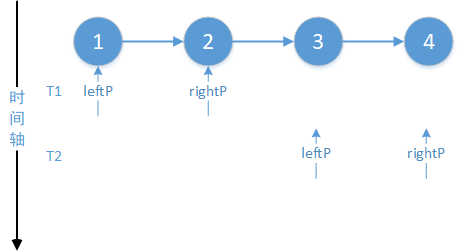
图1
见图1所示,我们在T1时刻交换[1, 2]两个节点,T2时刻交换[3, 4]。
这里易看出,此问题可以解为:
- 两两交换
- 迭代两两交换
对于问题1:
我们将总体链表的两两交换位置分别为若干相同的问题1,解法则有:
1 /* 2 head = [1, 2, 3, 4] 3 first, focus [1, 2] 4 */ 5 ListNode currHead; // and currHead.next = left 6 7 leftP.next = rightP.next; // 1->2->3 changed to 1->3 8 right.next = leftP; // 1->3 changed to 2->1->3 9 currHead.next = rightP; //upgrate head of piece of this pair
这里涉及到的额外节点信息是两个节点组的前置节点,即currHead;当我们交换[3, 4]时则有:
1 /* 2 head = [2, 1, 3, 4] 3 secod, focus [3, 4] 4 5 leftP point to 3, rightP 4. 6 */ 7 // currHead.next = leftP, here, currHead = ListNode(1) 8 9 // exchange node 3 and 4 10 leftP.next = rightP.next; 11 rightP.next = leftP; 12 currHead.next = rightP;
对于问题2:
截止到这里,我们已经探索到了问题1的解法,接下来需要做的就是将填补问题1间的缝隙,即将他们融合为一个整体,这里我们容易理解,在交换[3, 4]的时候,需要用到交换[1,2]后的靠后节点(这里为ListNode(1)),则可以理解我们在两两交换时,统一的需要用到currHead, 即两个节点[a, b]中 靠前节点a的前置节点,并需要在[a, b]交换位置后为下一对即将交换的节点更新它们所需的currHead。则我们可以将前两部分代码融合为:
1 ListNode leftP = head; 2 ListNode rightP = head.next; 3 4 ListNode currHead = dummyHead; //for head node 5 6 7 // iteration 8 leftP.next = rightP.next; 9 rightP.next = leftP; 10 currHead.next = rightP; 11 12 //update pos of currHead 13 currHead = leftP;
步骤罗列
我们已经对问题的解答有了核心的理解,这里将步骤进行进一步梳理:
- 初始化两个指针,一左一右;且为统一规则,采取哨兵机制;
- 迭代:节点交换,并更新下一对节点的靠前前置节点;
- 迭代终止条件为两指针均不为空;终止后返回哨兵节点的下一节点。
解题代码

1 public static ListNode solutionWithTwoP(ListNode head) { 2 if (head == null || head.next == null) { 3 return head; 4 } 5 6 //1. init pointers and dummyHead 7 ListNode dummyHead = new ListNode(-1); 8 dummyHead.next = head; 9 ListNode leftP = head; 10 ListNode rightP = head.next; 11 12 ListNode currHead = dummyHead; 13 14 //2. iteration 15 while (leftP != null && rightP != null) { 16 // exchange 17 leftP.next = rightP.next; 18 rightP.next = leftP; 19 currHead.next = rightP; 20 21 //update pos of currHead 22 currHead = leftP; 23 24 //move forward 25 leftP = leftP.next; 26 rightP = leftP == null? null : leftP.next; //attention here 27 } 28 29 return dummyHead.next; 30 }
View Code
复杂度分析
时间复杂度:我们对数据仅进行了一次遍历,所以时间复杂度为O(N);
空间复杂度:我们没有借助额外的容器,所以空间复杂度为常量级O(1)。
GitHub源码
完整可运行文件请访问GitHub。

