机器学习经典聚类算法 —— k-均值算法(附python实现代码及数据集)
- 2019 年 10 月 3 日
- 筆記
[toc]
工作原理
聚类是一种无监督的学习,它将相似的对象归到同一个簇中。类似于全自动分类(自动的意思是连类别都是自动构建的)。K-均值算法可以发现k个不同的簇,且每个簇的中心采用簇中所含值的均值计算而成。它的工作流程的伪代码表示如下:
创建k个点作为起始质心 当任意一个点的簇分配结果发生改变时 对数据集中的每个数据点 对每个质心 计算质心与数据点之间的距离 将数据点分配到距其最近的簇 对每一个簇,计算簇中所有点的均值并将均值作为质心 python实现
首先是两个距离函数,一般采用欧式距离
def distEclud(self, vecA, vecB): return np.linalg.norm(vecA - vecB) def distManh(self, vecA, vecB): return np.linalg.norm(vecA - vecB,ord = 1) 然后是randcent(),该函数为给点的数据集构建一个包含k个随机质心的集合
def randCent(self, X, k): n = X.shape[1] # 特征维数,也就是数据集有多少列 centroids = np.empty((k, n)) # k*n的矩阵,用于存储每簇的质心 for j in range(n): # 产生质心,一维一维地随机初始化 minJ = min(X[:, j]) rangeJ = float(max(X[:, j]) - minJ) centroids[:, j] = (minJ + rangeJ * np.random.rand(k, 1)).flatten() return centroids 对于kMeans和biKmeans的实现,参考了scikit-learn中kMeans的实现,将它们封装成类。
- n_clusters —— 聚类个数,也就是k
- initCent —— 生成初始质心的方法,’random’表示随机生成,也可以指定一个数组
- max_iter —— 最大迭代次数
class kMeans(object): def __init__(self, n_clusters=10, initCent='random', max_iter=300): if hasattr(initCent, '__array__'): n_clusters = initCent.shape[0] self.centroids = np.asarray(initCent, dtype=np.float) else: self.centroids = None self.n_clusters = n_clusters self.max_iter = max_iter self.initCent = initCent self.clusterAssment = None self.labels = None self.sse = None # 计算两个向量的欧式距离 def distEclud(self, vecA, vecB): return np.linalg.norm(vecA - vecB) # 计算两点的曼哈顿距离 def distManh(self, vecA, vecB): return np.linalg.norm(vecA - vecB, ord=1) # 为给点的数据集构建一个包含k个随机质心的集合 def randCent(self, X, k): n = X.shape[1] # 特征维数,也就是数据集有多少列 centroids = np.empty((k, n)) # k*n的矩阵,用于存储每簇的质心 for j in range(n): # 产生质心,一维一维地随机初始化 minJ = min(X[:, j]) rangeJ = float(max(X[:, j]) - minJ) centroids[:, j] = (minJ + rangeJ * np.random.rand(k, 1)).flatten() return centroids def fit(self, X): # 聚类函数 # 聚类完后将得到质心self.centroids,簇分配结果self.clusterAssment if not isinstance(X, np.ndarray): try: X = np.asarray(X) except: raise TypeError("numpy.ndarray required for X") m = X.shape[0] # 样本数量 self.clusterAssment = np.empty((m, 2)) # m*2的矩阵,第一列表示样本属于哪一簇,第二列存储该样本与质心的平方误差(Squared Error,SE) if self.initCent == 'random': # 可以指定质心或者随机产生质心 self.centroids = self.randCent(X, self.n_clusters) clusterChanged = True for _ in range(self.max_iter):# 指定最大迭代次数 clusterChanged = False for i in range(m): # 将每个样本分配到离它最近的质心所属的簇 minDist = np.inf minIndex = -1 for j in range(self.n_clusters): #遍历所有数据点找到距离每个点最近的质心 distJI = self.distEclud(self.centroids[j, :], X[i, :]) if distJI < minDist: minDist = distJI minIndex = j if self.clusterAssment[i, 0] != minIndex: clusterChanged = True self.clusterAssment[i, :] = minIndex, minDist ** 2 if not clusterChanged: # 若所有样本点所属的簇都不改变,则已收敛,提前结束迭代 break for i in range(self.n_clusters): # 将每个簇中的点的均值作为质心 ptsInClust = X[np.nonzero(self.clusterAssment[:, 0] == i)[0]] # 取出属于第i个族的所有点 if(len(ptsInClust) != 0): self.centroids[i, :] = np.mean(ptsInClust, axis=0) self.labels = self.clusterAssment[:, 0] self.sse = sum(self.clusterAssment[:, 1]) # Sum of Squared Error,SSE kMeans的缺点在于——可能收敛到局部最小值。采用SSE(Sum of Squared Error,误差平方和)来度量聚类的效果。SSE值越小表示数据点越接近于它们的质心,聚类效果也越好。
为了克服kMeans会收敛于局部最小值的问题,有人提出了一个称为二分K-均值的算法。该算法伪代码如下:
将所有点看成一个簇 当簇数目小于k时 对于每个簇 计算总误差 在给定的簇上面进行K-均值聚类(k=2) 计算将该簇一分为二之后的总误差 选择使得误差最小的那个簇进行划分操作 python代码如下:
class biKMeans(object): def __init__(self, n_clusters=5): self.n_clusters = n_clusters self.centroids = None self.clusterAssment = None self.labels = None self.sse = None # 计算两点的欧式距离 def distEclud(self, vecA, vecB): return np.linalg.norm(vecA - vecB) # 计算两点的曼哈顿距离 def distManh(self, vecA, vecB): return np.linalg.norm(vecA - vecB,ord = 1) def fit(self, X): m = X.shape[0] self.clusterAssment = np.zeros((m, 2)) if(len(X) != 0): centroid0 = np.mean(X, axis=0).tolist() centList = [centroid0] for j in range(m): # 计算每个样本点与质心之间初始的SE self.clusterAssment[j, 1] = self.distEclud(np.asarray(centroid0), X[j, :]) ** 2 while (len(centList) < self.n_clusters): lowestSSE = np.inf for i in range(len(centList)): # 尝试划分每一族,选取使得误差最小的那个族进行划分 ptsInCurrCluster = X[np.nonzero(self.clusterAssment[:, 0] == i)[0], :] clf = kMeans(n_clusters=2) clf.fit(ptsInCurrCluster) centroidMat, splitClustAss = clf.centroids, clf.clusterAssment # 划分该族后,所得到的质心、分配结果及误差矩阵 sseSplit = sum(splitClustAss[:, 1]) sseNotSplit = sum(self.clusterAssment[np.nonzero(self.clusterAssment[:, 0] != i)[0], 1]) if (sseSplit + sseNotSplit) < lowestSSE: bestCentToSplit = i bestNewCents = centroidMat bestClustAss = splitClustAss.copy() lowestSSE = sseSplit + sseNotSplit # 该族被划分成两个子族后,其中一个子族的索引变为原族的索引,另一个子族的索引变为len(centList),然后存入centList bestClustAss[np.nonzero(bestClustAss[:, 0] == 1)[0], 0] = len(centList) bestClustAss[np.nonzero(bestClustAss[:, 0] == 0)[0], 0] = bestCentToSplit centList[bestCentToSplit] = bestNewCents[0, :].tolist() centList.append(bestNewCents[1, :].tolist()) self.clusterAssment[np.nonzero(self.clusterAssment[:, 0] == bestCentToSplit)[0], :] = bestClustAss self.labels = self.clusterAssment[:, 0] self.sse = sum(self.clusterAssment[:, 1]) self.centroids = np.asarray(centList) 上述函数运行多次聚类会收敛到全局最小值,而原始的kMeans()函数偶尔会陷入局部最小值。
算法实战
对mnist数据集进行聚类
从网上找的数据集data.pkl。该数据集是mnist中选取的1000张图,用t_sne降维到了二维。
读取文件的代码如下:
dataSet, dataLabel = pickle.load(open('data.pkl', 'rb'), encoding='latin1') print(type(dataSet)) print(dataSet.shape) print(dataSet) print(type(dataLabel)) print(dataLabel.shape) print(dataLabel) 打印出来结果如下:
<class 'numpy.ndarray'> (1000, 2) [[ -0.48183008 -22.66856528] [ 11.5207274 10.62315075] [ 4.76092787 5.20842437] ... [ -8.43837464 2.63939773] [ 20.28416829 1.93584107] [-21.19202119 -4.47293397]] <class 'numpy.ndarray'> (1000,) [0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 9 5 5 6 5 0 9 8 9 8 4 1 7 7 3 5 1 0 0 2 2 7 8 2 0 1 2 6 3 3 7 3 3 4 6 6 6 ... 3 7 3 3 4 6 6 6 4 9 1 5 0 9 5 2 8 2 0 0 1 7 6 3 2 1 4 6 3 1 3 9 1 7 6 8 4 3] 开始使用之前编写的算法聚类,并多次运行保存sse最小的一次所得到的图。
def main(): dataSet, dataLabel = pickle.load(open('data.pkl', 'rb'), encoding='latin1') k = 10 clf = biKMeans(k) lowestsse = np.inf for i in range(10): print(i) clf.fit(dataSet) cents = clf.centroids labels = clf.labels sse = clf.sse visualization(k, dataSet, dataLabel, cents, labels, sse, lowestsse) if(sse < lowestsse): lowestsse = sse if __name__ == '__main__': main() 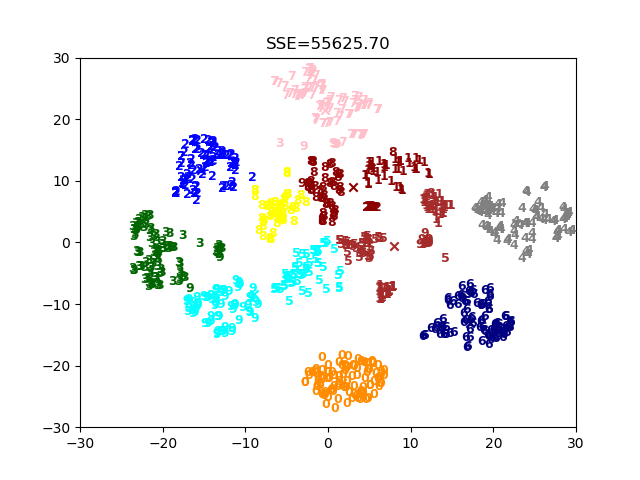
小结
聚类是一种无监督的学习方法。所谓无监督学习是指事先并不知道要寻找的内容,即没有目标变量。聚类将数据点归到多个簇中,其中相似数据点处于同一簇,而不相似数据点处于不同簇中。聚类中可以使用多种不同的方法来计算相似度(比如本文是使用距离度量)
K-均值算法是最为广泛使用聚类算法,其中的k是指用户指定要创建的簇的数目。K-均值聚类算法以k个随机质心开始。算法会计算每个点到质心的距离。每个点会被分配到距其最近的簇质心,然后紧接着基于新分配到簇的点更新簇质心。以上过程重复数次,直到簇质心不再改变。这种方法易于实现,但容易受到初始簇质心的影响,并且收敛到局部最优解而不是全局最优解。
还有一种二分K-均值的算法,可以得到更好的聚类效果。首先将所有点作为一个簇,然后使用K-均值算法(k=2)对其划分。下一次迭代时,选择有最大误差的簇进行划分。该过程重复直到k个簇创建成功为止。
附录
文中代码及数据集:https://github.com/Professorchen/Machine-Learning/tree/master/kMeans
