量子计算机编程(二)——QPU基础函数
- 2020 年 3 月 12 日
- 筆記
第二部分主要是QPU的基础功能,第一部分就像是我们有了哪些基本的语句,第二部分就是我们能写一些简单基础的函数,一些小模块,第三部分就是他的应用了。
先来看一下一个简单量子应用的结构:
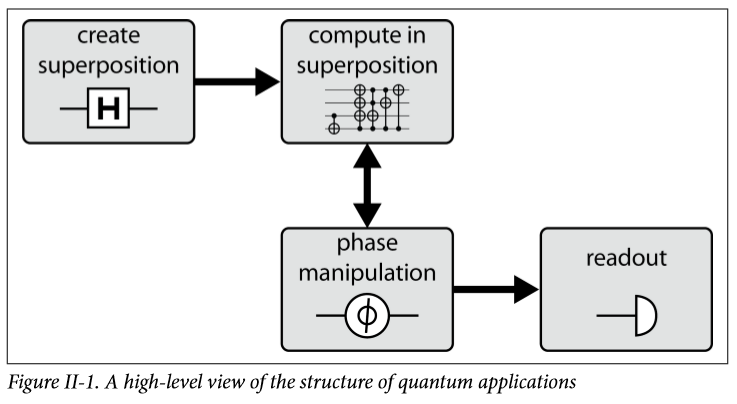
第一步,将量子态通过H门变成叠加态,很多应用的第一步都是H门,因为量子的叠加态正是她的优越性所在,所谓n个qubit可以表达 (2^n) 种状态, (2^n) 种可能性同时并行,这是叠加态带来的好处,要是一直使用基态,经典的不香吗?还便宜,量子的还需要在靠近绝对零度的温度下进行。
第二步,在叠加态中运算。
第三步,相位操作,叠加态中运算的结果当然也是叠加态的,但我们要获取,只能获取经典的信息,直接读的话,那他就是随机坍缩,信息丢失,当然你要是打算重复多次也行,但是有的时候,我们想要的并不是这个态的全部信息,我们可能需要的仅仅是他的一些特征,可能是一个序列的周期,我并不需要这个序列具体是什么,如此的话,可能一些相位变化操作就可以直接读取你想要的信息,这样更为方便。所以量子算法的设计,不仅仅要考虑量子怎么加速,还要考虑量子加速完了的结果能不能读出来。
第四步,读取。
量子算数逻辑
在量子之前,我们有经典算数和经典的数字逻辑,那么量子和经典有什么区别呢:
- 没有copy ,量子的信息不能复制,如果我们要把一个信息传给另一个,我们只能swap交换一下,或者我们还可以teleportation,总之,我们只能交换,不能赋值,具体一点来说,以前我们写程序的里面的赋值“=”是没有的。
- 可逆,除了测量,QPU上的所有操作都是可逆的。

说到逻辑,我们已经还记得数字逻辑里面学的全加器吧,c=a+b之类的操作,这个简单的加法后面是一堆的与或非门的结构,量子的也同样如此,结构也都差不多,不同之处就两点: (|arangle|brangle) 的进去 (|a+brangle|brangle) 的出来,因为量子要求可逆,他不会把a、b变成c,一旦合成了c,那就分不出a、b了,当然,你也可以 (|arangle|brangle|0rangle) 的进去 (|arangle|brangle|a+brangle),这样也是可以的;第二点就是叠加,这里的a、b不再是某个具体的数,而是一个叠加态。
如果是负数,那怎么表达呢?
和经典一样,我们可以负数的话,首位变成1。就像 000-0 001-1 002-2 003-3 100-(-4) 101-(-3) 110-(-2) 111-(-1),非常熟悉的配方的了。
关于条件判断呢,给大家看一个例子:
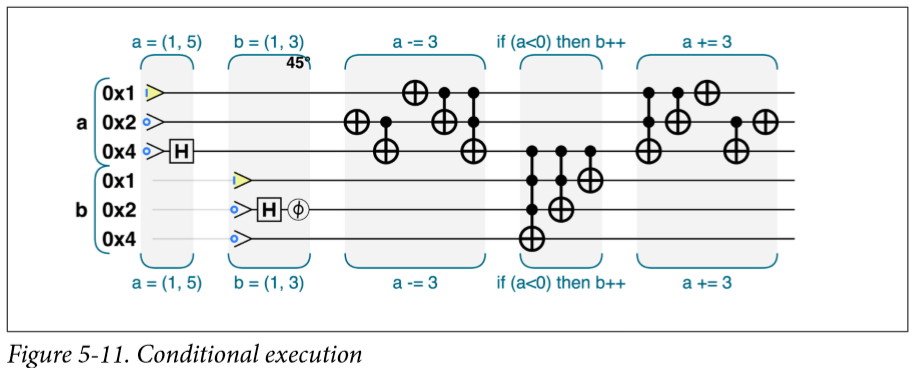
这是是如果a>3那么b就自增,如果没有,那就不用了,3不是很好的判断标准,但是0是啊,小于他的负数,直接首位编码就是1,所以,可以先-3,判断完了,增加好了,在把3加回来,办法总比问题多。
以上是量子和经典较为相似的部分,但是除此之外,量子还有新的特性,比如说:相位,接下来的篇幅都是属于他的。
振幅放大 Amplitude Amplification
我们先来说说振幅放大是什么:
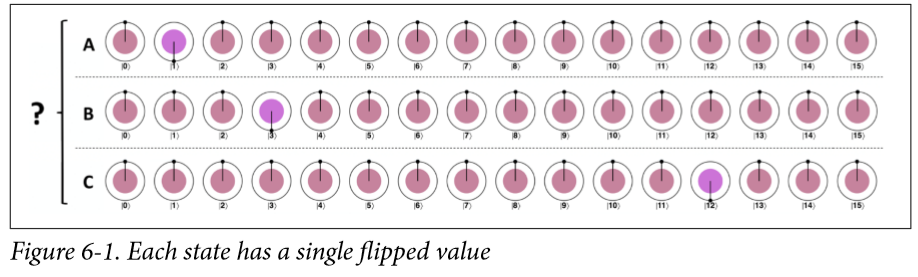

你觉得 Figure 6-1中的ABC三个qubit一样吗?不一样,直接看图很显然的不一样,虽然大家都是等概率的叠加态,但是他们相对相位180°的地方不一样。可是直接读,能读出来吗?即使我重复很多遍,但是他们的概率是一样的,no difference。但是,看图 Figure 6-3,就是可读的不一样了,振幅放大(AA)就是把他们从图6-1变成图6-3的方法。
现在我们已经只要了what和why了,接下来就是怎么进行how。
我们先来看一个单独的AA:
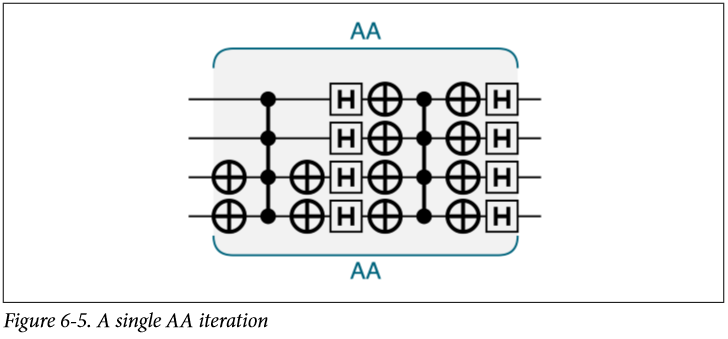
前面三步,也就是在4个H门之前是将这个叠加态中的某一个态给翻转他的相位,使他于其他态不同,接下来的几个步骤是把这个态的概率放大,至于问什么能放大,可以来看这篇 量子搜索算法 Grover search 这篇文章里主要是矩阵的角度,现在这个正好是一个具体的表现。
一次AA结束后,我们又回到了最初的相位,除了,我们翻转相位的那个态的振幅变大了,如果我们想要他继续变大,那么我们就继续AA,每一个AA都要包括将相位翻转的步骤。
你可能会疑惑,既然我们都知道要翻转哪一个态了,那为什么要费这么大的力气,这里,我们的翻转非常简单,就是找到这个态,然后翻转,上图就是两个not操作,但是在实际操作中,这可能是是一系列计算的结果。
AA一次就放大一些,再AA就再放大,那么是不是越多,就越能无线逼近1呢?

https://oreilly-qc.github.io/?p=6-2这是上面这个的实验,大家可以变换代码里面的 number_of_iterations,来验证一下刚刚的猜测,其实看图也能发现,(B_4)的概率是小于(B_3)的,why,事实上,这个概率大小是一个类似三角函数的存在:
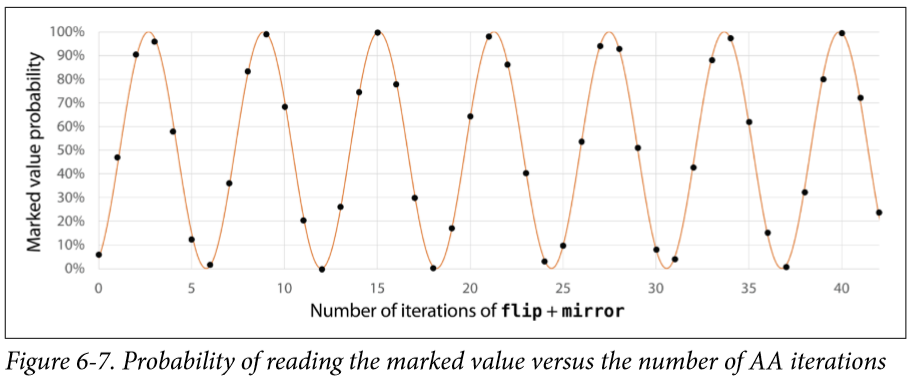
那么如何找到自己最合适的迭代次数呢?
书上给了一个未经过证明的公式Optimal number of iterations in amplitude amplification
[ N_{A A}=leftlfloorfrac{pi sqrt{2^{n}}}{4}rightrfloor ]
这本书是一本是实践为主的书籍,他还考虑了另一个问题,如果在这个里面我不仅仅要翻转一个态,我要翻转的是两个、三个又会怎么样呢?
https://oreilly-qc.github.io/?p=6-3 同样给大家一个连接,大家可以改变n2f这个数组的大小,和每次的迭代次数,看一看结果会有什么变化,当然这么做有些麻烦,也可以看下面的图,分别是4个qubit的情况下翻转2、3、7、8个态的效果长什么样,这里我就直接公布答案,随着翻转的态越来越大,这我们的这个三角函数的周期会越来越小。


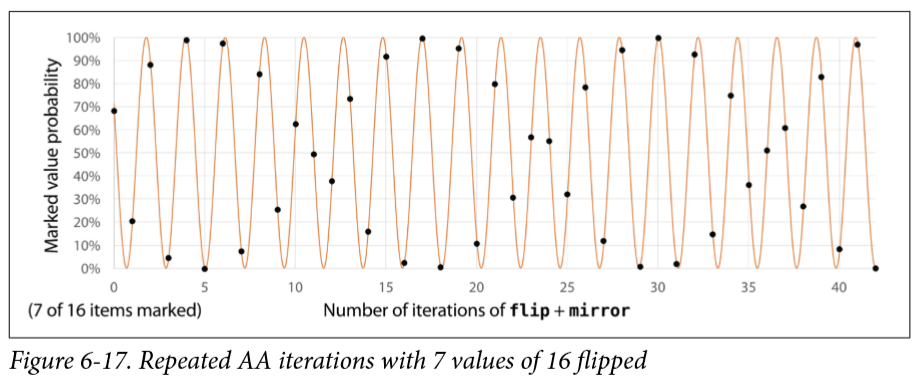

那么现在的最佳迭代次数又是多少呢?m是翻转的个数。
[ N_{A A}=leftlfloorfrac{pi}{4} sqrt{frac{2^{n}}{m}}rightrfloor ]
这里,我们再总结一下AA的意义,他把不可读的相位信息变成了可读的振幅信息。
量子傅里叶变换
提出一个技术,必定是为了解决一个问题,这里我们要解决的问题就是周期:
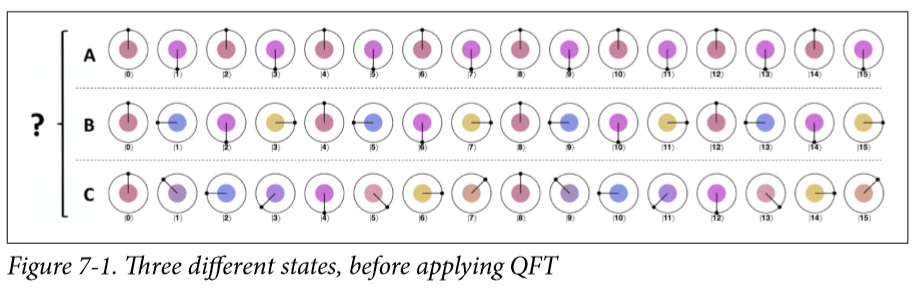
对于ABC这三个态,振幅放大也并不能很好的将他们区分,但是量子傅里叶变换(QFT)可以,他能够把上面这三个态变成下面这样:

A里面的有八个这样的周期,B里面有四个这样的周期,而C里面只有2个这样的周期,通过他们周期个数的不一样就可以轻而易举的把这三个态分辨出来。
量子傅里叶变换是一个封装好了的函数,直接调用.QFT就可以了。
var num_qubits = 4; qc.reset(num_qubits); var signal = qint.new(num_qubits, 'signal') // prepare the signal制备量子态C qc.label('prep'); signal.write(0); signal.hadamard(); signal.phase(45, 1); signal.phase(90, 2); signal.phase(180, 4); // Run the QFT直接调用 qc.label('QFT'); signal.QFT()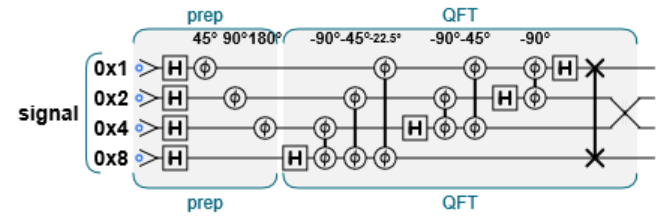
为什么这样就可以找到她的周期了呢?量子傅里叶变换
不过,QFT不是每次都能像现在这样获得这么好的结果的,像经典的傅里叶变换会有mirror-image,如下:

量子傅里叶也可能会有这种结果,我们同样也是取前面的一半:

选择量子傅里叶的好处在于,他很快,比快速傅里叶都还要快,他们的速度比值是这样的:
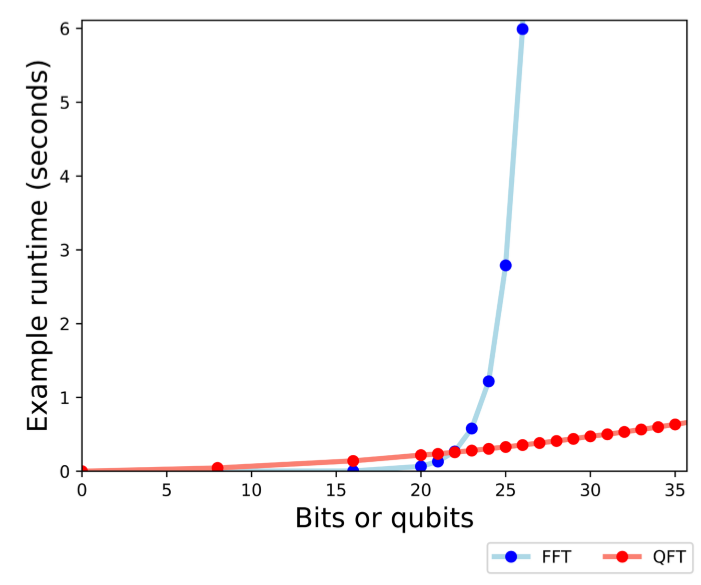
量子处理器的内部结构长这个样子:
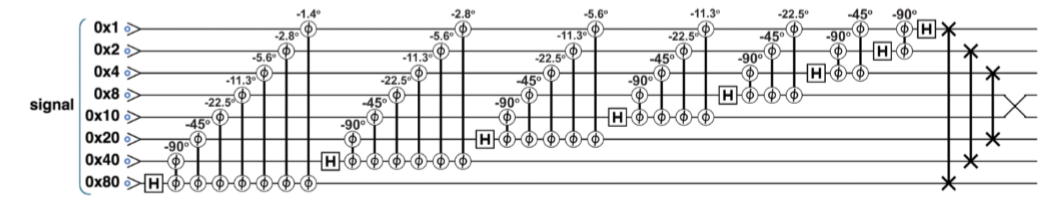
量子相位估计
这个关注的对象是量子操作的信息而不是量子寄存器的信息,每一个量子操作都可以用一个酉矩阵表示,而每一个量子态也可以用一个向量来表示,如果一个操作作用的量子态正好是他的特征向量会怎么样?
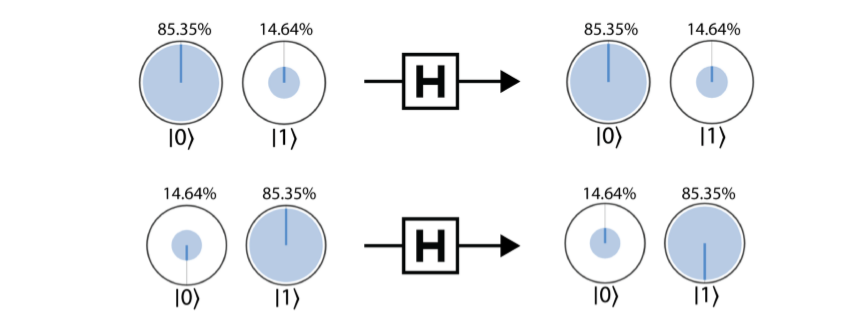
每一个操作都有自己的eigenstate和对应的eigenphase

所以相位估计究竟是做什么的呢?
假设我有一个操作U,以及操作的特征态(u_1,u_2,u_3,…),量子相位估计可以测出这些特征态所对应的特征相位。
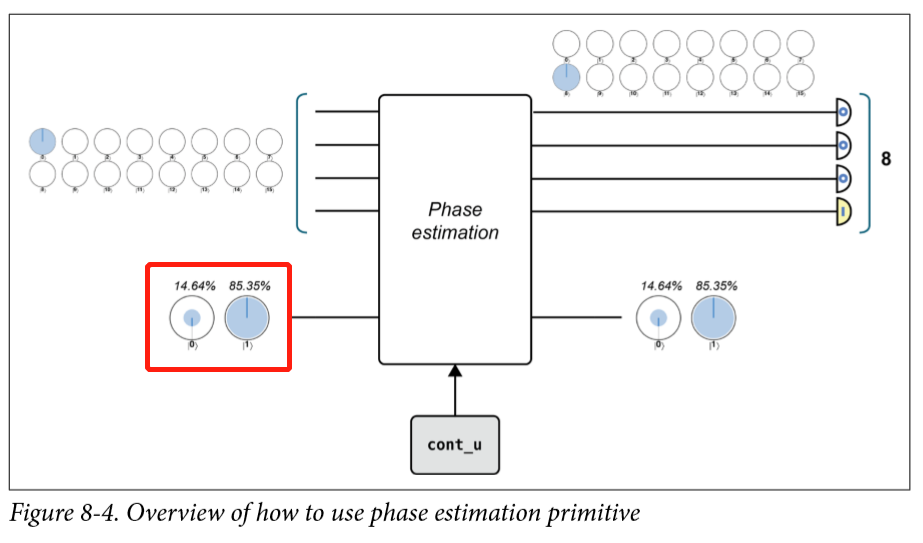
一个简单例子,cont_u是我们输入的操作,红框里,是这个操作的特征态,输出结果是8,这里有4个qubit,最大的输出结果可以是16,那么他对应的量子相位是:(8/16)*360°=180°,qubit的增加可以增加数据的精度,如果我们有最大误差要求,那么可以通过下面这个公式知道我们最小需要多少个量子比特:
[m=p+lceil log left(2+frac{1}{epsilon}right)rceil]
调用这个函数非常简单:qin是特征向量,cout_u是操作,qout就是我们的结果,她的位数取决于我们需要的精度。
// Operate phase estimation primitive on registers phase_est(qin, qout, cont_u); // Read output register qout.read();那么这个里面的操作又是长什么样子呢?

虽然看起来是上面在控制下面,但是仔细想一想 (-|0rangle|1rangle)你能分清楚这个负号是0还是1的吗?,相位信息就这样在qout里累加,最后一个逆傅里叶变换得到我们的结果。