无损卡尔曼滤波UKF(3)-预测-生成Sigma点
- 2020 年 3 月 11 日
- 筆記
无损卡尔曼滤波UKF(3)-预测-生成Sigma点
1 选择创建Sigma点
A 根据
已知上一个时间戳迭代出来的
后验状态 (x_{k|k}) 和后验协方差矩阵 (P_{k|k})
他们代表当前状态的分布。
Sigma点的数量取决于状态向量的维度
(n_{sigma} = 2cdot n_x + 1)
如果以两个维度的状态向量为例。就可以生成五个sigma点。
(X_{k|k} = [P1,P2,P3,P4,P5])
矩阵的每一列都代表一个Sigma点。
(X_{k|k} = [x_{k|k},x_{k|k}+sqrt[2]{(lambda+n_x)P_{k|k}},x_{k|k}-sqrt[2]{(lambda+n_x)P_{k|k}} ])
关于Lambda,是一个设计的参数,一般情况下,按下面的设置,效果还不错
(lambda = 3 – n_x)
求矩阵的平方根 => 找到矩阵A
(A = sqrt[2]{P_{k|k}} <= A^T A = P_{k|k})
第一个点就是状态向量的均值。
如果Lambda值大,Sigma点会距离均值点远一些。
生成Sigma点的代码(1)
/* 根据上述公式,完成生成Sigma点的函数 */ void UKF::GenerateSigmaPoints(MatrixXd* Xsig_out) { // 设置状态向量的维度 int n_x = 5; // 定义传播参数 double lambda = 3 - n_x; // 给定一个样例状态 VectorXd x = VectorXd(n_x); x << 5.7441, 1.3800, 2.2049, 0.5015, 0.3528; // 给定一个样例状态的协方差矩阵 MatrixXd P = MatrixXd(n_x, n_x); P << 0.0043, -0.0013, 0.0030, -0.0022, -0.0020, -0.0013, 0.0077, 0.0011, 0.0071, 0.0060, 0.0030, 0.0011, 0.0054, 0.0007, 0.0008, -0.0022, 0.0071, 0.0007, 0.0098, 0.0100, -0.0020, 0.0060, 0.0008, 0.0100, 0.0123; // 创建Sigma点的矩阵、一列代表一个Sigma点、 MatrixXd Xsig = MatrixXd(n_x, 2 * n_x + 1); // 计算矩阵P的平方根 MatrixXd A = P.llt().matrixL(); // 设置Sigma矩阵的第一列,一列代表一个Sigma点 Xsig.col(0) = x; // 设置Sigma矩阵剩下的点 for (int i = 0; i < n_x; ++i) { Xsig.col(i+1) = x + sqrt(lambda+n_x) * A.col(i); Xsig.col(i+1+n_x) = x - sqrt(lambda+n_x) * A.col(i); } // 打印结果 std::cout << "Xsig = " << std::endl << Xsig << std::endl; // 返回结果 *Xsig_out = Xsig; }B 扩充后创建Sigma点
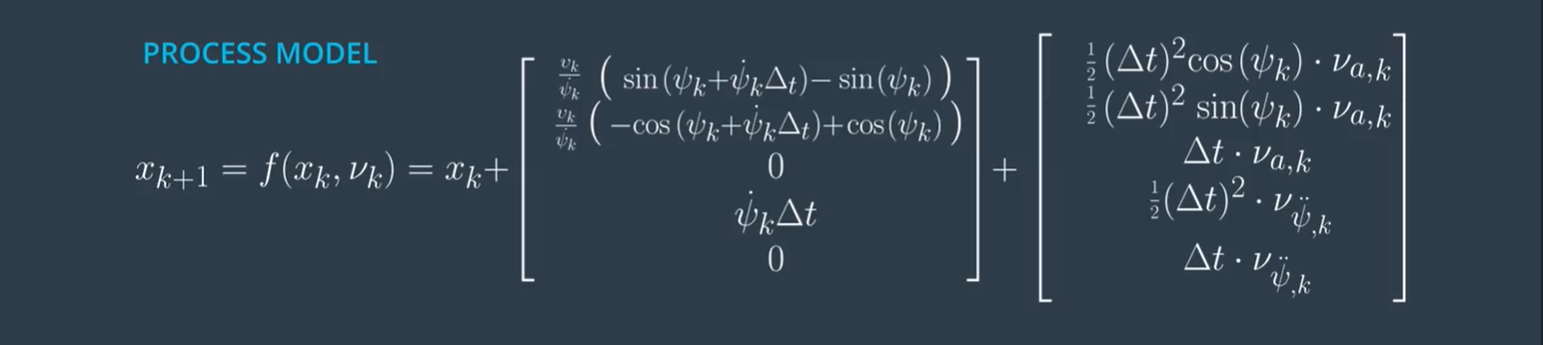

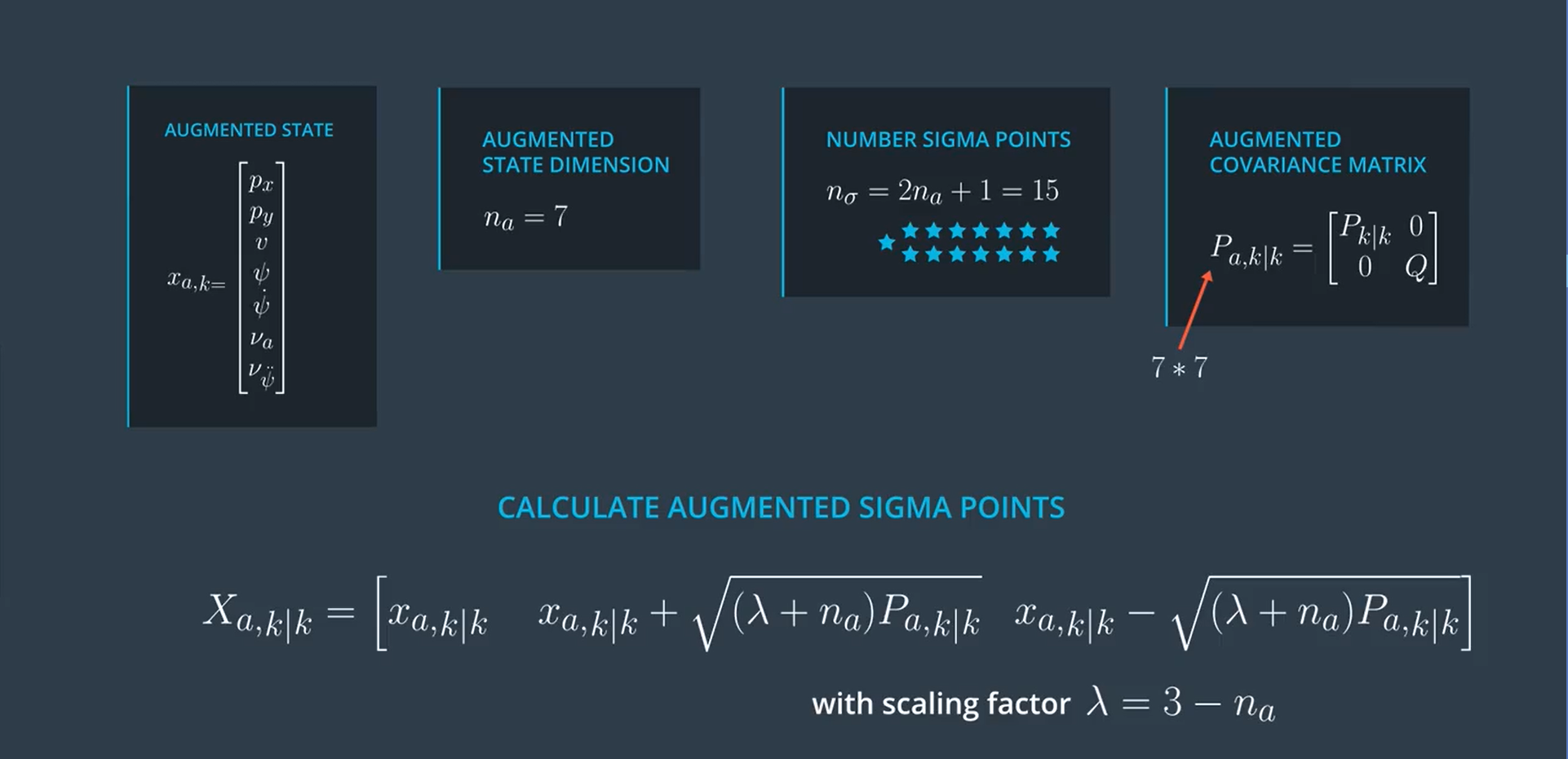
考虑到噪声的影响??
- 扩充状态的平均值中添加了两个噪声值。
- 纵向加速度项和角加速度项。均值为0 ,一定方差的正态分布。
- 他们的平均值为零,因此在平均状态的Sigma点,将他们的值设置为零。
- 用零填充扩充的协方差矩阵。
- 然后,使用topLeftcorner函数设置扩充的协方差矩阵的左上块。
- 方差放入增强矩阵的右下块。 该2×2块对应于矩阵QQ。
除了这次创建了更多的sigma点,其余部分与以前完全相同。
void UKF::AugmentedSigmaPoints(MatrixXd* Xsig_out) { // 维数 int n_x = 5; // 扩展后维数为7 int n_aug = 7; // Process noise standard deviation longitudinal acceleration in m/s^2 double std_a = 0.2; // Process noise standard deviation yaw acceleration in rad/s^2 double std_yawdd = 0.2; // 定义传播参数 double lambda = 3 - n_aug; VectorXd x = VectorXd(n_x); x << 5.7441, 1.3800, 2.2049, 0.5015, 0.3528; MatrixXd P = MatrixXd(n_x, n_x); P << 0.0043, -0.0013, 0.0030, -0.0022, -0.0020, -0.0013, 0.0077, 0.0011, 0.0071, 0.0060, 0.0030, 0.0011, 0.0054, 0.0007, 0.0008, -0.0022, 0.0071, 0.0007, 0.0098, 0.0100, -0.0020, 0.0060, 0.0008, 0.0100, 0.0123; // 创建扩充后的平均值向量 VectorXd x_aug = VectorXd(7); // 创建扩充后的状态协方差矩阵 MatrixXd P_aug = MatrixXd(7, 7); // 创建扩充后的Sigma矩阵 MatrixXd Xsig_aug = MatrixXd(n_aug, 2 * n_aug + 1); // 设置扩充后的平均值向量的参数值 x_aug.head(5) = x; x_aug(5) = 0; x_aug(6) = 0; // 设置扩充后的状态协方差矩阵 P_aug.fill(0.0); P_aug.topLeftCorner(5,5) = P; P_aug(5,5) = std_a*std_a; P_aug(6,6) = std_yawdd*std_yawdd; // 求P的平方根 MatrixXd L = P_aug.llt().matrixL(); // 设置Sigma矩阵其他位置的值 Xsig_aug.col(0) = x_aug; for (int i = 0; i< n_aug; ++i) { Xsig_aug.col(i+1) = x_aug + sqrt(lambda+n_aug) * L.col(i); Xsig_aug.col(i+1+n_aug) = x_aug - sqrt(lambda+n_aug) * L.col(i); } std::cout << "Xsig_aug = " << std::endl << Xsig_aug << std::endl; *Xsig_out = Xsig_aug; }
