从傅里叶级数（Fourier series）到离散傅里叶变换（Discrete Fourier transform）

从傅里叶级数（Fourier series）到离散傅里叶变换（Discrete Fourier transform）

一. 傅里叶级数（FS）

首先从最直观的开始，我们有一个信号\(x(t)\)（满足Dirichelet条件），先假设它是周期的，为了研究它，我们使用级数将之展开，展开方法如下

\[x(t)=\sum_{k=0}^{\infty}a_ke^{jkw_0t}\tag{1}
\]

现在问题就是如何求解\(a_k\)。因为三角函数是正交系，即

\[\forall \theta_1 \ne \theta_2 ,都有\int_{2\pi}e^{j(\theta_1 – \theta_2)t}\mathrm{d}t=0 \tag{2}
\]

这样我们就可以进行如下操作：

对（1）式左右同时积分：

\[\int_{T}x(t)e^{-jk\frac{2\pi}{T}t} \mathrm{d}t=\sum_{k’=o}^{k=\infty}\int_{T}a_ke^{j(k’-k)\frac{2\pi}{T_0}}\mathrm{d}t \tag{3}
\]

由于

\[\sum_{k=o}^{k=\infty}\int_{T}a_ke^{j(k’-k)\frac{2\pi}{T_0}}\mathrm{d}t=\begin{cases}
0,& k\ne k’\\
T,&k=k’
\end{cases}\tag{4}
\]

故（3）积分的结果如下：

\[\int_{T}x(t)e^{-jk\frac{2\pi}{T}t} \mathrm{d}t =a_kT
\]

于是我们得到了\(a_k\)：

\[a_k=\frac{1}{T}\int_{T}x(t)e^{-jk\frac{2\pi}{T}t} \mathrm{d}t \tag{5}
\]

这样我们就把一个周期信号分解成了一系列模为\(a_k\)的复周期信号的组合，形象表示就是这样：

1

图片来源：傅里叶分析之掐死傅里叶教程//zhuanlan.zhihu.com/p/19763358（推荐大家看看）

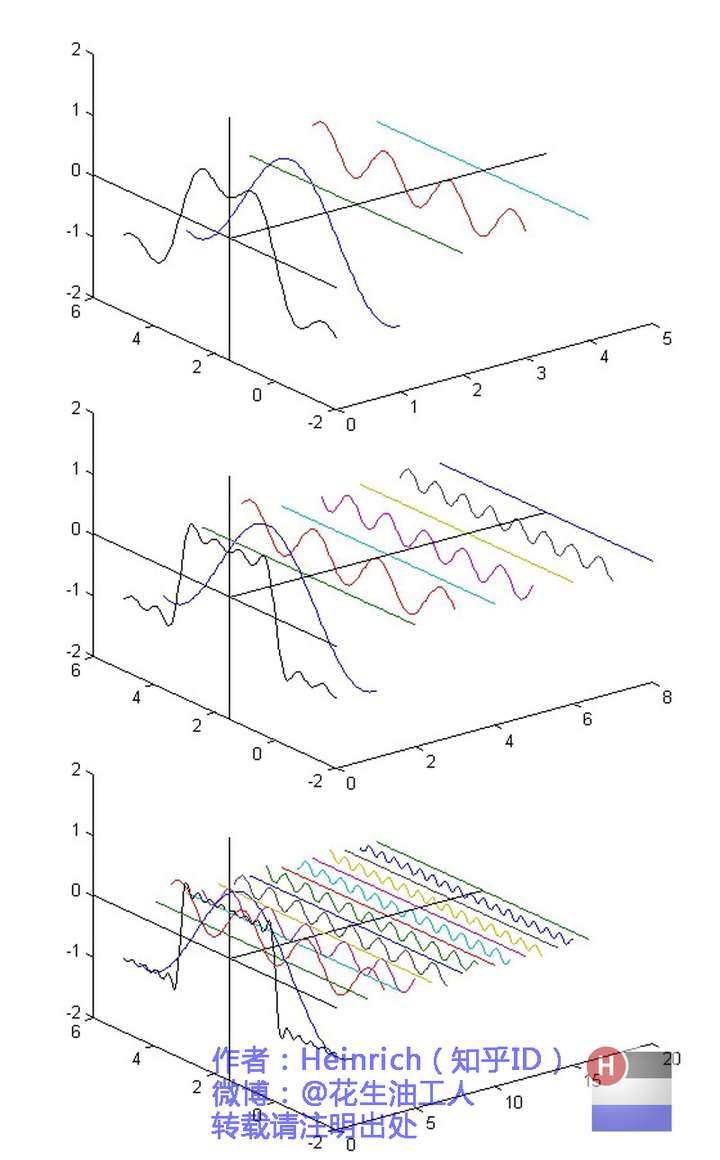
OK，到这里我们成功将一个周期信号分解成了傅里叶级数。但是这里也有两个问题依然困扰着我：

1.首先（相信大家也注意到了我第一句标黄的内容），非周期有限信号能不能展开成傅里叶级数呢？

比如，如果有一个函数，它是这样的：

\[s(t) = \begin{cases}
x(t), & 0\le t \le T \\
0, & others \\
\end{cases}\\ \tag{6}
x(t)是一个周期为T，满足Dirichelet条件的函数
\]

我们同样可以在0-T上做积分，并且得到\(s(t)\)的\(a_k\)和\(x(t)\)的\(a_k\)是相同的，也就是说，可以把s(t)写成：

\[s(t)=\begin{cases}
\sum_{k=0}^{\infty}a_ke^{jkw_0t},& 0\le t\le T\\
0,& others
\end{cases} \tag{7}
\]

但是咱也理解，这样的一个式子大概率不能叫做级数，充其量叫个级数的一部分。不过我们主要研究信号，就不关心这些数学概念了。那么对于这样的一个信号，傅里叶级数还能不能表达它的频谱特性呢？它的频谱跟\(x(t)\)又有什么联系呢？,这两个问题我们在第二部分解答。

2. 三角函数系的正交性强调的是一个周期内的积分，但是没有说一定是最小正周期，如果我们在\(2T\)、\(3T\)或者\(nT\)上积分，会发生什么呢？

回答这个问题之前，我们先对傅里叶级数做一个比较统筹的显示，我们不妨以\(w\)作为横坐标，以\(a_ke^{jkw_0}\)的强度（也就是\(||a_ke^{jkw_0}||=|a_k|\)）作为纵坐标，构建一个二维直角坐标系(数据大小是随便给的)：

2

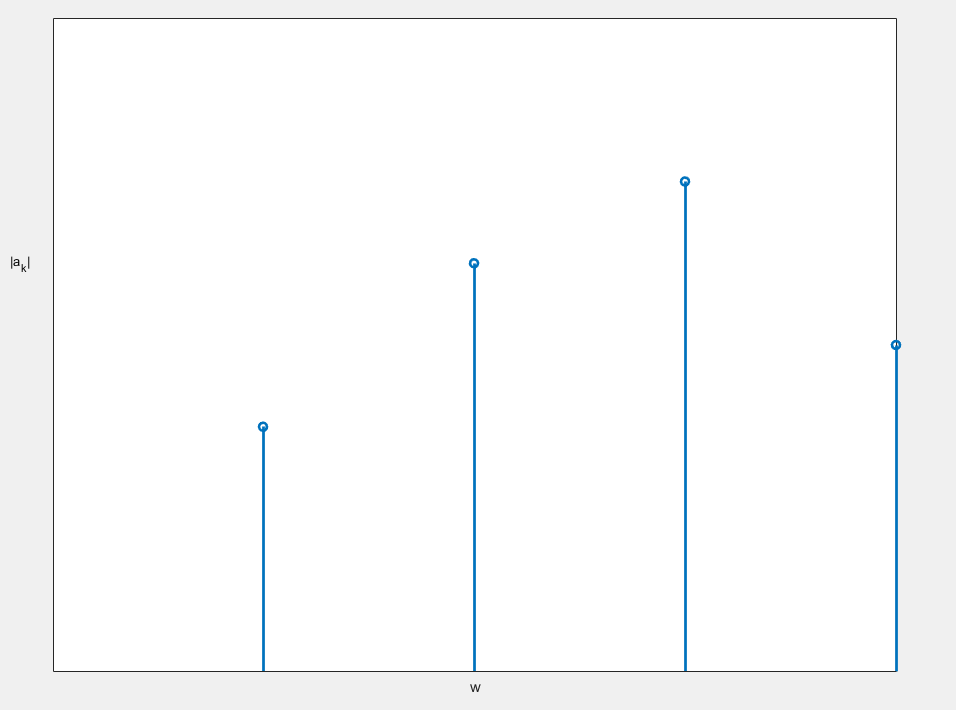
分析这个图，我们知道每两个”柱子“之间的距离应该是\(\Delta w=w_0=\frac{2\pi}{T}\)，所以，如果我们增大T，两个数据之间的距离就会变小，如下：

3

4

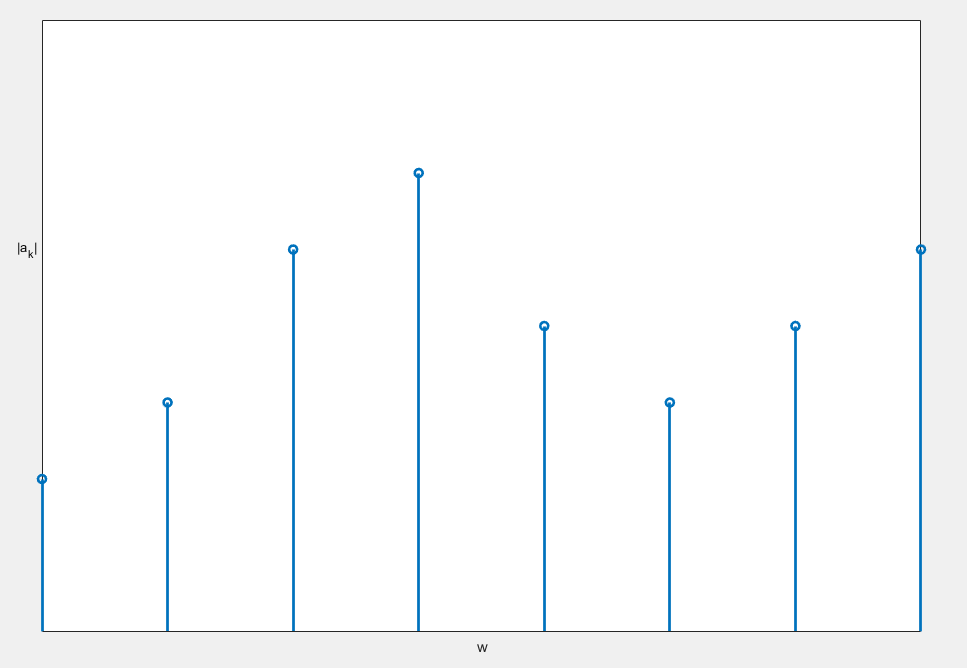
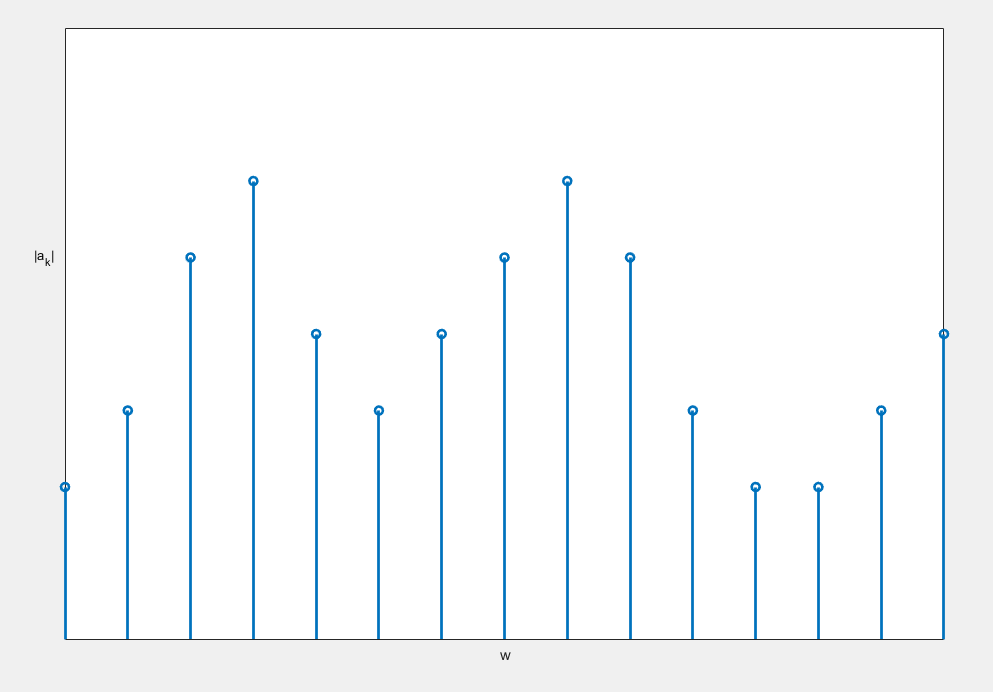
可以看到，\(T\)越大,两个数据之间的横轴距离就越小，不妨做个猜想：当\(T\to \infty\)时，这个离散的谱就变成了连续谱。是这样吗？应该说对有限信号是这样的，对无限周期信号则不是，这是为什么呢？请看下一节傅里叶变换的解读。

二. 傅里叶变换（FT）

2.1 傅里叶变换的推导

接着前面的猜想进行分析，为了得到可靠结论，我们进行如下数学分析：

接着（5）式开展：

\[a_k=\lim_{T\to \infty}\frac{1}{T}\int_{T}x(t)e^{-jk\frac{2\pi}{T}t} \mathrm{d}t
\]

用\(w_0=\frac{2\pi}{T}\)替代\(T\)，同时将\(x(t)\)表示出来:

\[\begin{split}
x(t)&=\sum_{k=0}^{\infty}[\lim_{T\to \infty}\frac{1}{T}\int_{-\infty}^{+\infty}x(t)e^{-jk\frac{2\pi}{T}t} \mathrm{d}t]e^{jk\frac{2\pi}{T}t} \\
&=\sum_{k=0}^{\infty}\lim_{w_0\to 0}[\frac{w_0}{2\pi}\int_{-\infty}^{+\infty}x(t)e^{-jkw_0t} \mathrm{d}t]e^{jkw_0t}\\
\end{split}
\]

当\(w_0\to 0\)时，可用\(w_0=\mathrm{d} w\)表示它，此外，对于\(kw_0\)的累加就变成了积分（累加步长\(kw_0\)无限小）,故而上式变成了：

\[x(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}[\int_{-\infty}^{+\infty}x(t)e^{-jwt} \mathrm{d}t]e^{jwt}\mathrm{d}w
\]

这样我们实现了将一个信号分解成连续的频谱，而这个频谱就是：

\[X(w)=\int_{-\infty}^{+\infty}x(t)e^{-jwt} \mathrm{d}t \\
x(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}X(w)e^{jwt}\mathrm{d}w \tag{8}
\]

（6）式就是傅里叶变换的基本形式，当然有些地方可能将系数\(\frac{1}{2\pi}\)进行了一些变换,比如：

\[X(w)=\sqrt{ \frac{1}{2\pi} }\int_{-\infty}^{+\infty}x(t)e^{-jwt} \mathrm{d}t \\
x(t)=\sqrt{ \frac{1}{2\pi} }\int_{-\infty}^{+\infty}X(w)e^{jwt}\mathrm{d}w
\]

这些都是小细节，咱们就不在意了。

2.2 周期函数的傅里叶变换

观察（8）这个式子，我们很快又发现了另外一个问题，积分区域是无穷，而周期函数在无穷区间积分，那必然是发散的，怎么解呢？

我们是这样处理的：

  1. 首先将\(x(t)\)表示成傅里叶级数：

    \[x(t)=\sum_{k} a_ke^{jkw_ot}
    \]

  2. 对级数做傅里叶变换，也就是：

    \[X(w)=\sum_{k} F(a_ke^{jkw_ot})=a_k\sum_{k} F(e^{jkw_0t})\tag{9}
    \]

​ 于是问题转化成了如何求\(e^{jkw_0t}\)的傅里叶变换，这个就要使用傅里叶变换的基本性质了：信号乘以\(e^{jw_0t}\)相当于傅里叶变换\(X(w)\)进行频移\(w_0\)， 这个我们也可以顺便证明一下：

\[若X(w)=\int_{-\infty}^{+\infty}x(t)e^{-jwt} \mathrm{d}t \\
\begin{split}
则X'(w)&=\int_{-\infty}^{+\infty}[x(t)e^{jw_0t}]e^{-jwt} \mathrm{d}t\\
&=\int_{-\infty}^{+\infty}x(t)e^{-j(w-w_0)t} \mathrm{d}t\\
&=X(w-w_0)
\end{split}
\]

​ 又由于：

\[1=\frac{1}{2\pi}\int_{-\infty}^{+\infty}2\pi \delta (t)e^{jwt}\mathrm{d}w \\
故F(x)=2\pi \delta (t)
\]

​ 所以：

\[F(1\cdot e^{jkw_0t})=F_{w-w_0}(1)=2\pi \delta (w-w_0)\tag{10}
\]

​ 把（10）代入（9），就得到了周期函数的傅里叶变换：

\[X(w)=a_k\sum_{k} 2\pi \delta(w-kw_0)\tag{11}
\]

可以看出，周期函数的傅里叶变换是一系列冲击串，这个倒也符合我们的直觉：

傅里叶变换每个\(X(w)\)可以理解为信号频率为\(w\)的分量的大小，对于周期信号，它的每一个频率分量都是一个无限长信号，所以每一个分量的能量都是无穷的，所以在频谱上就表示为冲击串了。

2.3 有限长非周期信号的傅里叶变换

好了，现在我们来解答第一节中的第二个问题：有限长非周期信号的傅里叶变换和周期信号频谱的关系。

对于有限长信号：

\[s(t) = \begin{cases}
x(t), & 0\le t \le T \\
0, & others \\
\end{cases}\\ \tag{6}
x(t)是一个周期为T，满足Dirichelet条件的函数
\]

可以换一种表达方式:

\[s(t)=x(t)[u(t)-u(t-T)]
\]

要求\(F[s(t)]\)，我们首先需要以下几个结论：

  1. 时域相乘等于频域卷积，证明:

    \[若Z(w)=X(w)*Y(w),则\\
    \begin{split}
    z(t)&=F^{-1}(Z(w))\\
    &=\int_\infty [\int_\infty X(m)Y(w-m)\mathrm{d}m]e^{jwt}\mathrm{d}t \\
    &=\int_\infty X(m)[\int_{\infty}Y(w-m)e^{jwt}\mathrm{d}t]\mathrm{d}m\\
    &=\int_\infty X(m)y(t)e^{jmt}\mathrm{d}m\\
    &=x(t)y(t)\\
    得证
    \end{split}
    \]

    注：如果从采用\(z(t)=x(t)y(t)出发，去证明Z(w)=X(w)*Y(w)\)会比较麻烦。

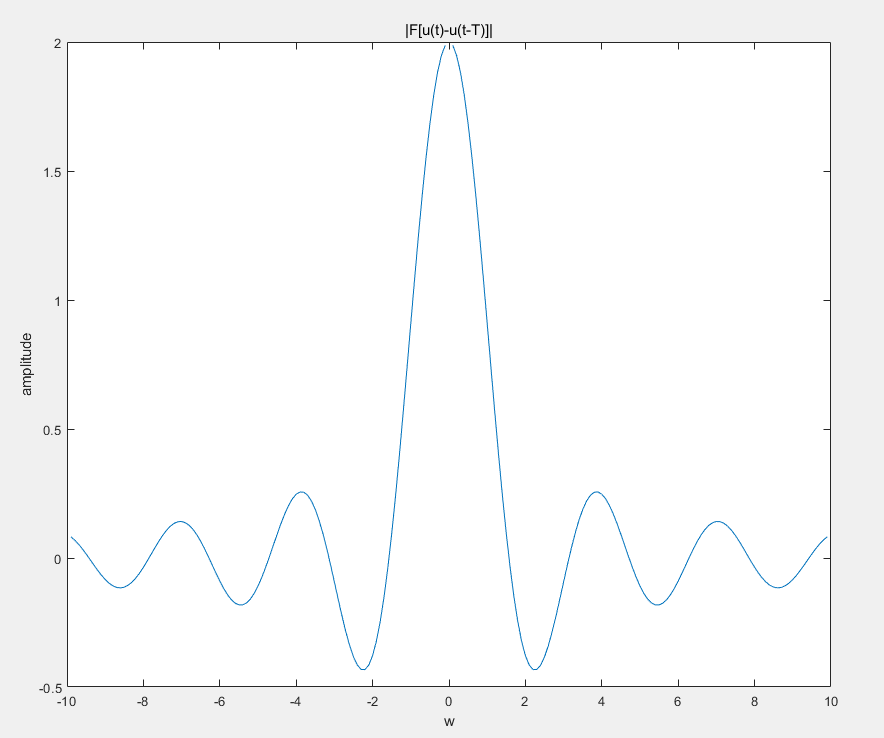
  2. \(F[u(t)-u(t-T)]=\frac{1-e^{-jwt}}{jw}\)，这个就很好证明了:

    \[\begin{split}
    F[u(t)-u(t-T)]&=\int_{0}^{T}x(t)e^{-jwt}\mathrm{d}t\\
    &=\frac{1-e^{-jwt}}{jw}
    \end{split}
    \]

    这个函数展现的频谱图像如下：

    6

好了，我们现在可以开始计算（6）式\(s(t)\)的傅里叶变换了：

\[F(s(t))=F(x(t))*F[u(t)-u(t-T)]\\
在(11)有X(w)=a_k\sum_{k} 2\pi \delta(w-kw_0)\\
故F(s(t))=2\pi a_k\sum_{k}\delta(w-kw_0)*\frac{1-e^{-jwt}}{jw}\\
又有\delta (t-t_0)*x(t)=x(t-t_0)
\]

及\(\sum_{k}\delta(w-kw_0)*\frac{1-e^{-jwt}}{jw}\)就是\(F[u(t)-u(t-T)]\)以\(kw_0\)移位叠加,一些一组图表示这个过程：

简单起见，我们令|X(w)|为：

对它进行卷积，也就是将下面两个信号叠加：

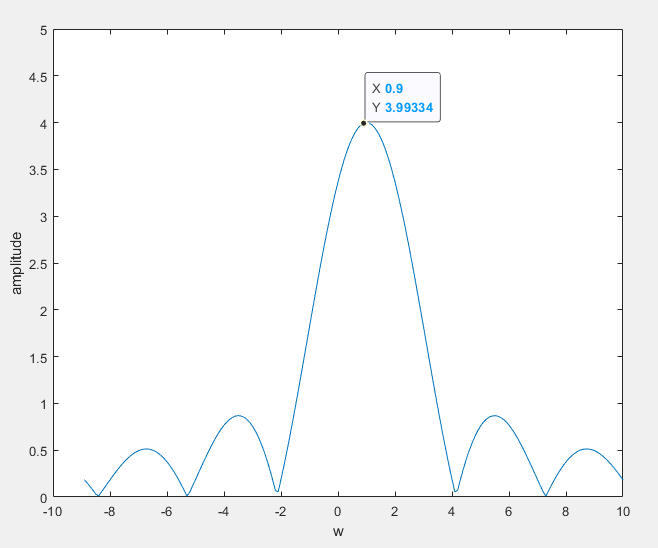
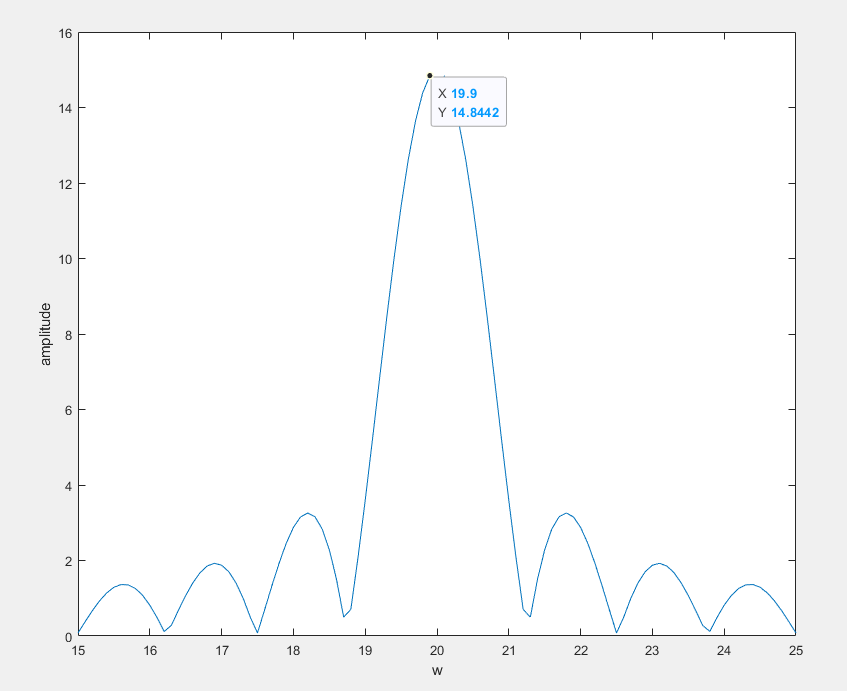
于是得到|S(w)|：

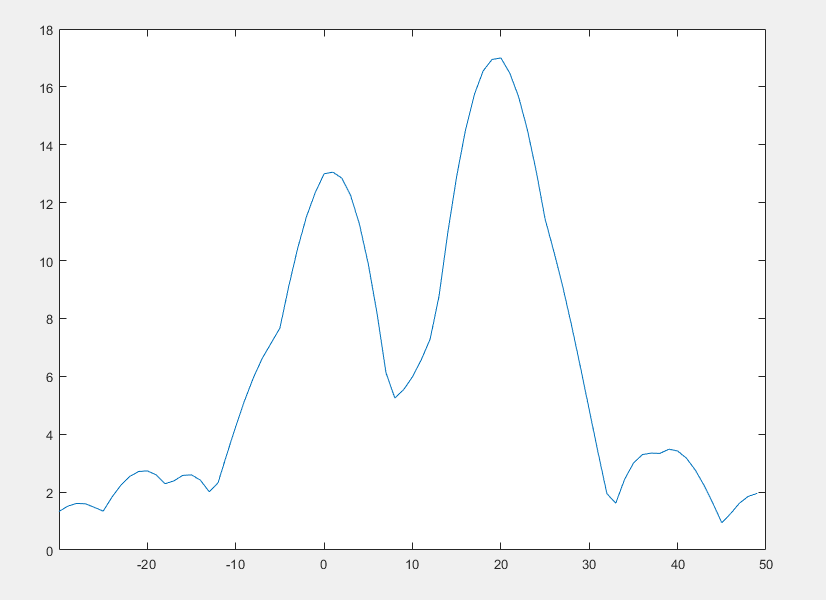
图不咋好看，可能是频率分辨率没调好，但是大概样子大家能看清楚了，也就是在周期信号的频谱里的冲击串变得平滑了，或者换句话说，原来集中在某个\(kw_0\)频率的能量一部分泄露到了全频域。

这个在物理意义上也比较好理解，把周期信号截断了，实际上是把一部分信号值变成了0，从某个值突然变到0(x(T)->0)，这里没有平滑过渡，是一个突变，而我们知道，突变包含所有频率分量。

至此，我们完成了傅里叶级数到傅里叶变换的推导。

三、时域离散化

在实际应用中，我们大多处理的是数字信号，也就是时域离散的信号，我们来看看时域离散对信号频谱的影响。

这个时候，我们可以把信号表示为

\[x(n)=x(t)\sum_{n=-\infty}^{+\infty}\delta(t-nT)\\
x(t)是连续信号，T是采样周期（即每隔T时间从x(t)上取一个点）
\]

根据（10），利用傅里叶变换的对偶性，可以得出：

\[F(\sum_{n=-\infty}^{+\infty}\delta(t-nT))=w_0\sum_{k=-\infty}^{+\infty}\delta(w-kw_0)\\
w_s=\frac{2\pi}{T}
\]

所以\(x(t)\)的傅里叶变换为：

\[F(x(n))=w_s\sum X(w)*\delta (w-kw_s)=w_s\sum X(w-kw_s)\\
X(w)是x(t)的傅里叶变换
\]

也就是说，\(x(n)\)的傅里叶变换就是下\(x(t)\)的傅里叶变换以\(w_s\)为周期，移位叠加。

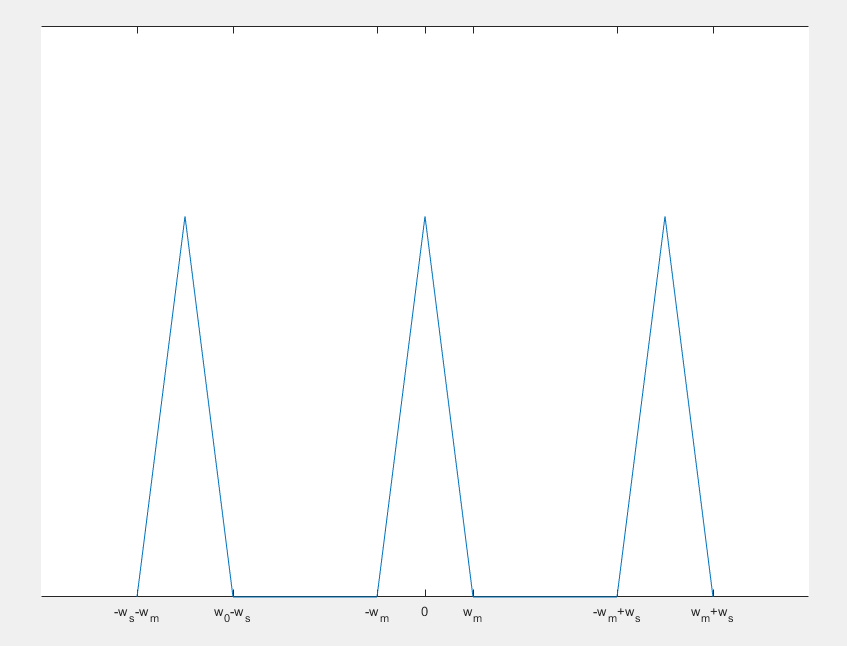
如上图，假设中间的三角形就是\(X(w)\)，则它经过移位叠加后得到的上图就是\(F(x(n))\)。

从这张图我们也可以看出一个重要的定理——奈奎斯特采样定理：采样频率需要高于信号最高频率的两倍，因为如果不能满足

\[w_m < w_s-w_m,即w_s>2w_m
\]

就会发生频谱混叠（上图的两个相邻三角形叠在一起了）。

这样我们就得到了时域离散信号的傅里叶变换，但是显然，这样得到的频谱也是连续的，计算机存储的是离散信号，那么如何将频域也离散化呢？请看下节。

四、DFT

回顾前面的内容，我们发现，满足频域离散的只有一种信号，那就是周期信号。于是让信号离散化的方法就呼之欲出了：

假设我们采集到的N个数据其实是一个周期信号的一个周期，或者换句话说，我们把这N点数据以N为周期进行延拓，那么接下来要做的就是对一个周期信号的傅里叶变换了，又时域是离散的，傅里叶变换就退化成了傅里叶级数形式：

\[F(x(n))=\sum_{n=0}^{N-1}x(n)W_N^{nk}\\
W_{N}^{nk}=e^{-j\frac{2\pi}{N}nk}（为什么要搞出个W_{N}^{nk}呢？我也不知道）
\]

现在好了，时域和频域都是离散的了，而且频域和时域一样只有N个点。并且通过上面时域离散造成频域以采样角频率\(w_s\)拓展的结论，我们可以知道，这个数字频谱，其实就是在长度为\(w_s\)的区间内插入了N个点，所以没两个点之间的频率间隔为

\[\Delta w=\frac{w_s}{N}
\]

这个\(\Delta w\)也叫做频率分辨率，也就是通过这个频谱能区分的两个频率最小的间隔。

这里我们再对模拟角频率\(\Omega\)和数字角频率做一个区分：

在模拟域，频率\(f\)表示的是一个信号每秒重复变化的次数，模拟角频率\(\Omega=2\pi f\)表示的就是单位时间内信号相位角变换的弧度。可以把一个重复的信号想象成一个点做圆周运动，\(f\)表示它单位时间绕了多少圈，\(w\)表示它单位时间转过多少弧度。

在数字域，我们同样可以通过单位时间信号相位角的该变量来表示角频率，但是数字域只有单位1，无连续时间的概念，长度为N的序列，两个点相隔的时间是\(\frac{1}{f_s}\)，所以数字域的“时间”每改变1，角度改变应该是：

\[\begin{split}
w&=\Omega \frac{1}{f_s}\\
&=\Omega T
\end{split}
\]

上式还可以写作\(w=2\pi \frac{f}{f_s}\)，又由采样定理知\(f_s>2f\),所以\(w<\pi\)，但是我们常常取数字频域的\(0-f_s\)进行研究，也就是说\(w\)最大取到\(2\pi\)(实际上是0移位一个周期得到的)，可见：\(w\)被限制在了[0 \(2\pi\)]，所以我们也称数字角频率\(w\)为归一化频率。

其实上述所有的推导都能在《信号与系统》和《数字信号处理》教材里找到，我只是做了一个整理和总结，建议大家还是精读课本，写书的人一般比写博客的人强。

Tags:

VirMach 便宜 VPS

QNews

QNews