📃 时间与概念增强的深度多维项目反应理论的可解释知识跟踪

• 2022 年 2 月 28 日
• 筆記
• papers

Time-and-Concept Enhanced Deep Multidimensional Item Response Theory for interpretable Knowledge Tracing

“时间与概念增强的深度多维项目反应理论的可解释知识跟踪” 阅读笔记

Abstract

知识追踪(KT)，由于知识状态的潜在和时变特征，一直具有挑战性。传统的心理测量框架缺乏提取练习或考生的丰富表现的能力，而基于深度学习的KT模型有着强大的特征提取能力，但是它存在着明显的缺点，即可解释性弱。此外，现有的框架通常不能适当地处理时间因素，因为它们中的大多数只是通过应用随机过程来模拟知识状态随时间的波动。

在这篇论文中提出了一个时间和概念增强的深度多维项目响应理论(TC-MIRT)，该框架将多维项目响应理论的参数集成到一个改进的递归神经网络中。具体来说，其构建了两个增强的组件，以使模型能够执行趋势预测，并在每个特定的知识领域中生成可解释的参数。在两个真实数据集上实现的实验表明，TC-MIRT框架在性能预测任务上优于最先进的KT方法。此外，广泛的案例分析也表明，TC-MIRT的可解释参数可以用于评估学生的优缺点。

1 Introduction

本文最重要的两个内容：两个增强的组件——一个时间增强的层，以增强模型的时间趋势预测能力；一个概念增强的模块，将多维IRF参数投影到能力坐标（或概念空间）中。

文章的主要贡献总结如下：

• 1.成功地将多维IRT与深度网络相结合，并建立了一个始终优于最先进的KT框架的综合模型。
• 2.一种具有时间增强功能的组件，具有特殊的门结构（zoom gate），提供了对缺失数据和输入问题之间的大时间间隔的鲁棒性。
• 3.通过概念增强模块，TC-MIRT能够生成可解释的多维参数，包括项目辨别能力、项目难度和学生能力，所有这些参数都可以直接用于特定技能（概念）维度的诊断。
• 4.作者与两个真实的数据集上的几个最先进的KT模型进行了比较，并设计了一系列的实验来说明作者的方法在性能预测和可解释性方面的优越性。

2 Related work

本文将现有KT方法分为三类：

• 第一类包括心理测量领域的基于IRT的范式；
• 第二类包括一系列传统的概率模型；
• 最后一种是最近提出的基于深度学习的模型。

2.1 Item Response Theory

项目反应理论(IRT)，也被称为潜在特征理论，是一系列心理测量范式的一个通用术语。一般来说，它对测试项目与测试者相应反应之间的关系进行建模。

IRT假设存在一个潜在的特征，代表每个考生的能力，该特征可以通过考生对项目的反应来观察到。正确响应的概率 \((p)\) 可以通过标准的2参数项目响应函数(IRF)来计算：

\(p=\frac{1}{1+e^{-a(θ-b)}}\)，(1)

参数 a 和 b 分别代表项目辨别和项目难度
θ 表示测试者的能力

虽然IRT能够用其可解释的参数来描述学生的行为，但一维的潜在特征限制了其应用——因为在现实世界的辅导场景中，考生通常需要多种能力才能正确地回答一个问题。以数学为例，要解决一个高级代数问题，考生需要掌握矩阵操作、行列式计算和向量运算等几种基本技能，用一维参数对所有三个概念进行建模是不现实的。

通过扩展IRT，研究人员提出了一系列多维IRT(MIRT)模型来表征多维空间中每个测试者的潜在特征。MIRT模型通常通过在不同维度上结合能力信息的方式被分为两种典型类型：补偿模型和非补偿模型。

• 补偿模型假设一个潜在特征的缺陷可以通过对其他维度的高度掌握来弥补；
• 非补偿模型将多维潜在特征视为独立的元素，并通过单一的IRT任务来解决每个特征。对于综合辅导系统，非补偿性模式可能是不合适的，因为知识概念被认为是相互关联的。

基于irt的模型具有预定义的参数具有很强的可解释性。然而，它们缺乏用它们简单的参数设置来编码更复杂的学生和项目特性的能力，这使得很难跟踪灵活的用户行为和问题属性。

2.2 Probabilistic knowledge tracing models

对于一种通用的智能辅导系统，贝叶斯知识跟踪(BKT)通常被认为是一种有效的解决方案和一个强大的基线。通过假设一个二元隐知识状态（掌握和非掌握），BKT能够利用一个隐马尔可夫模型来建模学习和回答的过程。

在最初的BKT框架中，学生和能力被平等对待，这使得该模型不可能发现个体之间的潜在差异。知识状态的二进制表示也限制了BKT的语境化，特别是在应用于高级教育资源时。研究人员试图通过引入特定学生、特定技能的参数和扩大更多的状态来改善BKT。然而，这些方法可能代价昂贵，因为它们中的大多数都是基于各种统计正则化的。

其他的概率模型，如部分可观察的马尔可夫决策过程和性能因素分析，也可以显示出与BKT相当的性能。但这些模型受到高计算复杂度或它们对人类工程特征的需求的限制。

2.3 Deep-learning based models

深度知识追踪(DKT)利用递归神经网络来模拟知识状态的转换，并能够捕获题目和学生的复杂高维特征。然而，深度网络的密集结构使得DKT不可能生成具有特定物理意义的参数。研究发现，当DKT应用于真实数据集时，它可能会导致各种问题：

• 1.跨时间的输出概率不一致
• 2.与实际学生的反应不兼容的反直觉预测

动态键值记忆网络(DKVMN)利用记忆增强神经网络(Mann)和注意机制来追踪学生在不同维度[14]中的能力。为了进一步使DKVMN具有可解释的参数，通过结合改进的DKVMN和IR，实现了一个名为Deep-IRT的合成框架。Deep-IRT似乎同时利用了DKVMN的特征提取能力和IRT的有意义的IRF参数，但它仍然存在一些缺陷：

• 首先，DKVMN和Deep-IRT都使用内存大小为N的内存矩阵来发现练习的“底层”模式或概念，其中N只是一个超参数。在这些模型的训练过程中，记忆矩阵被随机初始化，不提供额外的信息来帮助它们找出哪个记忆槽对应于哪些实际的知识概念。
• 其次，Deep-IRT采用一维IRT参数，因此缺乏处理补偿性知识概念的建模能力（即，学生对不同知识的能力应该共同对输出有贡献）。
• 最后，由于没有利用时间信息，它仍然缺乏模拟不同时间间隔后学生能力变化的能力。

3 TC-MIRT framework

本文专注于离线场景的KT应用。
对每个学生 \(i\)，目标如下：

• 1.学习模型参数：通过一系列问题 \(\{q^i_0,…,q^i_{t-1}\}\)、相关知识标签(含多个) \(\{k^i_0,…,k^i_{t-1}\}\) 和学生回答 \(\{r^i_0,…,r^i_{t-1}\} (t=1,2,…,T-1)\)，其中，T表示学生 i 的完整序列的长度，\(r^i_t\)可以是 \(0/1\)，也可以是 \([0.0,1.0]\) 内的小数。
• 2.预测学生对下一个问题 \(q^i_t\) 的回答。
  

3.1 输入层

该模型中，在时间 t，首先使用嵌入矩阵\(E∈R^M\)将问题索引序列转换为密集向量序列\((e_0，e_1，…，e_t)\)(\(e_t∈R^{d_e}\)，其中\(d_e\)表示每个问题的该层输出向量的大小)。
同时，\(q_t\)的知识概念标签用多热编码\(k_t∈\{0,1\}^K\)表示，其中 K 表示潜在的知识概念或技能的数量。
为了将 \(k_t\) 与 \(e_t\) 结合起来，全连接层的实现如下：

其中 \(e^k_t∈R^d{k_e}\)为知识编码，\(d^k_e\)为隐藏向量的中间长度。

在实验中，把组合的问题向量\(x_t∈R^{d_e}\)具有与 \(e_t\) 相同的形状，隐藏向量的大小可以根据实际的训练资源进行调整。最后，采用零填充的方法，将问题与学生回答信息合并，形成最终的输入：

其中 0 =（0,0，……，0\()_{de}\)是一个固定长度的零向量，用于区分成功尝试 \((r_t=1)\) 和失败尝试 \((r_t=0)\)。

对于有评分率 \((r_t∈[0.0,1.0])\) 的ITSs，0.6.9和0.9代表考生的能力完全不同。在这种情况下，本文应用以下实证方法来获取更多的信息：

其中，\(1=(1,1，……，1)_{d_e}，R_t=(r_t，r_t，……，r_t)_{d_e}\)
m 是整个数据集的中位数评分率，它用于区分类似成功的尝试和类似失败的尝试

3.2 时间增强的循环层

一个标准的LSTM块可以用以下方程来表示：

对于普通的在线辅导系统，获得每个学生的完整学习轨迹（即学生尝试过的每个问题都是不现实的）。换句话说，模型需要能够处理缺失的数据和样本之间的不同时间间隔。因此，如果应用一个标准的LSTM，主要存在两个问题：

• 首先，长时间和短时间几乎肯定会导致学生能力发生不同程度的变化，但最初的LSTM记忆块没有考虑到时间特征。
• 其次，对于那些学习能力相对较强的学生来说，他们的掌握水平在一段时间后可能会变得更高——无论在这段时间内是否有记录的（题目，回答）对。

然而，由于输出 \((f_t)\) 位于[0,1]之间的遗忘门限制，历史单元状态 \(C_{t−1}\) 在标准LSTM中总是减弱。总之，原始的LSTM不能对这种与时间相关的能力增长或下降进行建模（或预测）。

如图2所示。为了模型能够具有预测时间间隔后学生能力波动的能力，作者首先在原始隐藏状态 \(h_{t−1}\) 之后增加一个额外的密集层来引入时间信息；然后用一个名为 zoom gate 的新结构来取代遗忘门。改进后的内存块可以用数学方法表示如下：

• \(s_t\) 是时间增强的隐藏状态，它存储了学生在开始回答问题 \(q_t\) 之前的知识条件
• z 表示缩放门，\(v_t∈R^{d_t}\) 表示步骤 t 处的时间戳。使用二进制序列化向量 \(v_t\) 来表示时间戳：
  • 首先，将格式为“%Y-%m-%d%H：%M：%S”的时间戳转换为浮数（以秒为单位）
  • 然后除以比例因子 ε 并将其转换为16位二进制向量

一般来说，只要得到的时间戳向量可以覆盖最长的序列（即第一个输入和最后一个输入之间时间间隔最长的序列），就可以选择任意合适的尺度因子。对于每个学生，第一个回答问题的时间戳总是设置为零。

如方程式（16），缩放门(zt)的输出，用于加权历史单元格的状态。在TC-MIRT中，根据当前的输入信号（包括当前的时间戳），可能想要削弱或加强历史单元格状态的每个维度，因为学生的能力可能会随着时间的推移而改变。从理论上讲，当门输出较小时，sigmoid激活和tanh激活函数都能在一定程度上削弱单元格状态。

然而，作者实证发现，tanh激活函数始终优于simoid激活函数（以很小的幅度）。作者认为，通过允许负输出，缩放门在放大时间间隔的影响和建模学生能力的波动方面变得更加灵活。
此外，在方程13）尺度因子 \(λ_k\) 和偏置 \(λ_b\) 也可以通过改变门输出 \(z_t\) 的范围来实现更显著的减弱和增强效应。

例如，当 \(λ_k\)=1.05和 \(λ_b\)=0.05时，门输出zt的范围从[−1.0,1.0]变为[−1.0,1.1]，这意味着当 \(z_t\) 的值在(1.0,1.1]之间时，历史能力状态 \(C_{t−1}\) 可以加强。

请注意，在Eq（13），变放门也将 \(C_{t−1}\) 作为输入的一部分，这通常被称为窥视孔连接。使用窥视孔结构在缩放向量 \(z_t\) 的计算中引入长期能力信息，这是由经验教学经验激发的：优秀学生和困难学生之间的差距越来越大。换句话说，缩放效应的大小部分受学生的学习历史的控制。

3.3 概念增强模块

如上所述，缺乏可解释性是大多数基于深度学习的KT模型的最大障碍之一。将心理测量模型和深度网络相结合似乎是一个很好的解决方案。深度irt试图通过学生能力网络和困难网络来生成可解释的参数。但是，它所使用的内存矩阵是随机初始化的，不应用外部信息来监督每个概念槽的分布或概念之间的内部关系。更具体地说，我们无法理解某个概念槽的潜在物理意义，也无法将一个隐藏的状态映射到技能空间。
为了解决这一问题，我们提出了一个基于二参数MIRT函数和概念矩阵的概念化模块。

3.4 MIRT.

在TC-MIRT中，作者使用了一个2参数的补偿性MIRT(M2PL)模型来估计在时间 t 时出现正确响应 \(p_t\) 的概率。

其中，\(a_t∈R^K，θ_t∈R^K和d_t∈R\) 分别表示项目区分度、学生能力和项目难度。
然后，应用一个简单的均方误差损失函数，如下：

与特定技能对应的k维特征空间也被称为 θ 坐标。将公式（19）中的指数项分解为:

其中，\(b_{t,j}\)表示第 j 个 θ 坐标的项目难度。本文通过将标量 \(d_t\) 扩展到一个向量 \(b_t∈R^K\)中，从而可以直接比较每个θ坐标中学生的能力和项目难度。

3.5 Concept Matrix

为了生成适当的M2PL参数并提高模型的可解释性，本文提出了一个概念矩阵 \(M_c∈R^{d_c×K}\)，它将学生的行为和问题特征投射到相同的空间中。 \(M_c\) 的每一列都可以看作是一个概念标签的嵌入，而 \(d_c\) 则是嵌入的大小。

文章提出了 Concept2Vec 来学习由上下文间相关信息丰富的概念嵌入。在 Concept2Vec 中，继承Word2Vec的假设：“如果两个单词具有相似的上下文，那么它们将具有相似的语义。”，并利用问题层次结构来形成训练语料库。在实际的教育数据集中，问题的层次结构可以是包含一组相关问题的任何东西——一门课、一本书或一个章节。

如图3所示，为了形成每个训练样本，本文将每个问题层次下的所有问题的概念标签连接起来，删除重复的标签。然后，利用连续bag of words（CBOW）架构，其中预训练模型从周围概念的窗口中预测目标概念。在预训练任务完成后，\(M_c\) 将在性能预测任务的训练过程中进行微调。

在TC-MIRT中，本文使用一个能发现 θ 坐标之间内在关系的权重向量作为区分项。具体来说，a 的计算方法如下：

其中，\(I_t\) 为输入技能 \(k_t\) 的索引列表，\(\hat{m}_t\)为输入概念嵌入的平均池化向量。Then，取 \(\hat{m}_t\) 和概念矩阵的点积来形成权值向量 \(a_t\)。 公式（21）、（22）和（23）的过程本质上等同于注意机制：平均知识嵌入 \(\hat{m}_t\) 作为查询，概念矩阵 \(M_c\) 由关键插槽组成。

在这种情况下，输出 \(a_t\) 实际上是输入概念和 bank 中每个概念之间的相似性，从而作者在本模块中做出了核心假设：当模型预测特定输入练习 \(q_t\) 时，重点应该是放上 \(k_t\) 对应的 θ 坐标以及其他与 \(k_t\) 密切相关的技能。
换句话说，具有相似嵌入的概念应该具有更强的内部相关性，并共同为模型预测做出贡献。

max(·) 函数来将 \(a_t\) 中的所有负元素转换为零:

• 希望我们的权重向量具有与标准IRT中的辨别项相似的非负元素
• 希望消除具有负注意权重的非相关概念所带来的副作用

其他M2PL参数通过以下确定：

可以看出，项目难度 \(b_t\) 依赖于组合问题向量 \(x_t\)，而学生能力 \(θ_t\) 依赖于时间增强的隐藏状态。此外，通过概念矩阵将它们都映射到 θ 坐标上，使我们可以理解模型参数的实际意义。

4. 实验

4.1 数据集

• iFLYTEK 由科大讯飞有限公司提供，由广泛使用的在线辅导系统薛收集，为高中生提供全年教育资源。在科大讯飞研究中，学生的回答用 [0.0,1.0] 之间的分数来表示。
• KDD 这个开源数据集是用于教育数据挖掘挑战的KDDCup2010数据的一部分。原始记录由步骤序列（子级）组成，而不是问题（父级）。在这种情况下，我们将每个问题的评分率计算为成功步骤的比率（不请求任何提示）。例如，如果一个问题有三个步骤，而一个考生在其中两个步骤中取得了成功，则回答将变为0.66。

4.2 实验设置

• 数据分区。 在每个数据集上，首先随机抽取90%的学生，并使用他们的学习记录作为训练集；剩下的10%学生的记录作为测试集。然后，从测试集中删除所有在训练集中看不见的问题，以确保在实验中，KT模型不会出现看不见的问题。从每个训练集中，还抽取10%的学生作为验证集来开发我们的模型。对于评估的每个模型，在每个数据集上运行3次，并使用平均结果作为最终结果。

• 参数设置。模型的批为32，初始学习率为0.0001。应用一个指数学习率衰减，衰减率为0.05。在这两个数据集中，都使用一个16位向量和一个100（ε）的比例因子来表示时间戳，从每个学生的第一个问题的最大时间间隔为\(2^{16}\) ∗100秒（约2.5个月）。\(d_e、d^k_e和\ d_c\) 分别被设置为经验值75、75和 32。图4显示了具有不同缩放门上界的TC-MIRT的模型性能，可以看出，当上界设置为1.1时，得到了最优结果。
  
  此外，本文还实现了Dropout（dropout=0.5）和批归一化等算法，以避免过拟合，这对模型性能有轻微的提高。在这两个数据集上，最多训练模型50个epochs以获得最佳性能，所有可训练权值都用Xavier初始化初始化，并用Adam优化算法进行更新。

• 模型比较。为了帮助理解TC-MIRT中每个关键提案所带来的具体影响，论文实现了以下两个TC-MIRT的简化版本：

  • 1.T-MIRT：在概念增强模块中，有两种设计带来了模型的可解释性——预先训练好的概念矩阵和基于输入概念计算出的概念权重(见方程式（22）和（23）)：前者提供了发现概念之间相关性的先验知识，而后者作为一个监督信号，将theta坐标投射到实际概念中。在T-MIRT中，通过以下方法删除了这两种设计：

    • 首先，用一个随机初始化的可训练权重 W 替换概念矩阵：
      –
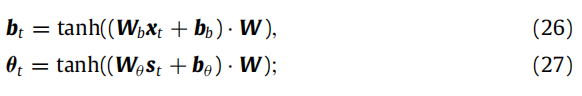
    • 其次，用以下计算的区分项替换概念权重：
      

  • 2.Deep-MIRT：在Deep-MIRT中，进一步从T-MIRT中删除了时增强组件，用标准的LSTM单元替换了时增强单元。

4.3 结果与分析

• 评估指标。对于具有二进制响应的数据集，当考虑二进制响应时，通常使用曲线下面积(AUC)作为评价度量。然而，一些研究人员发现，AUC对浮点数目标的效果较差。因此，在本实验中，选择均方根误差(RMSE)作为主要度量。

  • Note. AUC仍然是作为一个参考指标来计算的。如果\(r_t≥m，让r_t=1，否则r_t=0\)

  为了对模型参数的可解释性进行数值评估，文章还提出了以下三个指标：
  
  其中PCC（·，·）为两个变量之间的皮尔逊相关系数，α 和 β 分别表示不同学生和问题的集合。

  学生因变量 \(ER_i=(E(r_i，c_1)，…，E(r_i，c_M))\)，其中 \(E(r_i，c_1)\) 表示学生 i 在所有带有概念标签 \(c_1\) 的问题上取得的平均得分率。

  类似地，题目相关变量 \(\{VR_j，ER_j\}\)，
  \(VR_j= (Var(r_{c_1}，j)，…，Var(r_{c_M}，j))和ER_j=(E(r_{c_1}，j)，…，E(r_{c_M}，j))\)，其中\(Var(r_{c_1}，j)\) 表示所有学生在概念标签 \(c_1\)在问题 j 上的得分率的方差。

  这些度量被用于直观地度量每个θ坐标和相应的概念标签之间的相关性。

  对一系列问题进行预测的可解释的KT模型，模型输出的一致性也很重要。本文采用了[27]中提出的两个指标 (m1和m2) 来评估模型的一致性：
  
  其中 \(k^i_t\) 是 t 时刻问题的多热概念标签，\(T_i\) 表示学生 i 的问题序列的总长度。\(g^i_{t−1}∈0,1\) 是上一步的ground-truth 输出。
  为了将评分比转换为二进制输出，\(if\ r^i_t≥m, g^i_t=1\)，否则，\(g^i_t=0\) 其中 m 为表1所示的评分率的中位数。

  当一个学生在某个问题上失败时，我们更倾向于在下一步获得较低的能力，反之亦然。因此，m1和m2的值越高，从预测一致性的角度来看，模型就越好。m1和m2的主要区别在于，m2同时考虑了变化的方向和幅度。

• 性能预测。如图5显示了KT模型在整个训练过程中的验证损失，总的来说，TC-MIRT的收敛速度与其他模型相当，说明增强后的模块对模型拟合没有影响。在科大讯飞和KDD上的模型性能 如表2所示，总的来说，在线场景可以通过其动态学习机制产生显著的性能改进，但我们的离线方案(T-MIRT和TC-MIRT)在RMSE和AUC上始终优于在线模型

  
  
  此外，由于T-MIRT的性能远优于DeepMIRT，故认为时间增强组件在提高性能预测能力方面发挥着重要作用。

• 趋势预测。与标准的IRT相比，TIRT也产生了显著的改进，显示了时间信息在KT任务中的有效性。为了进一步评估我们的建议的趋势预测能力，我们通过在原始测试数据中随机减少10%、30%、50%、50%、70%的交互，构建了4个不完整的测试集。在科大讯飞上，每个学生的记录都跨越了一个高中学年，因此不完整数据中的问题会发生巨大的变化，这使得KT模型很难做出精确的估计。如图6、我们的建议能够抵抗不同级别的数据缺失。当省略超过50%的交互作用时，TC-MIRT具有强大的趋势预测能力，其RMSE值比包括在线TIRT在内的其他模型要小得多。

• 可解释的弱点诊断。图8(a)表示所有概念之间的 M×M 协同矩阵，位置值 (i,j) 表示“问题层次”级别中 \(c_i和c_j\)之间的归一化共现频率。例如，如果 \(c_i和c_j\) 同时出现在10个层次上，而 \(c_i\)存在于20个层次上，则标准化频率将为10/20=0.5。(i, j) 处的数值越大，ci和cj相关的机会就越大。
  

  同时，图8(b)显示了经过预训练和微调后的概念矩阵中所有嵌入之间的余弦相似性矩阵。可以看出，这两个矩阵具有相似的分布，特别是在热区域，说明微调过程没有影响概念矩阵的可解释性，概念之间的相关性得到了很好的保持。

  学生弱点的诊断对于个性化的运动推荐至关重要，它也是评估KT框架的可解释性的一个令人信服的标准。在TC-MIRT中，这是通过使用M2PL参数 a、b 和 θ 来实现的。

  为了举一个如何使用TC-MIRT来诊断学生的弱点的例子，从KDD数据集中随机选择一个学生，以及一个模型认为学生无法正确回答的随机问题\((q_r)(p_r=0.32)\)。
  

  问题 \(q_r\) 有两个人类标记的概念\(\{c_0, c_2\}\)。结果的参数如图9所示。可以看出，模型在 \(c_2和c_5\) 上生成了最大的指数项，而 \(c_0\) 则不在在前五名名单中。在KDD中，知识概念 \(c_2和c_5\) 是指分别指寻找 y，任何形式；寻找 x，任何形式。

  直观地说，这两种技能（find x, find y）是高度相关的，用于测试类似的考生的能力。如图8c所示，概念 \(c_2和c_5\) 的概念嵌入具有相对较高的余弦相似度，约为0.82，这也解释了我们模型的结果。
  
  另一个人类标记的概念 \(c_0\) 指的是识别单位，这是一种常见的技能，经常出现在不同的问题中，因此模型中没有给它分配高权重。
  总之，可以把这种失败的尝试归因于主要在 \(c_2和c_5\) 方面的不熟练。

表3显示了这两个数据集的测试集上的模型参数的PCC分数。由于MIRT和T-MIRT中没有提供与概念相关的信息，所以没有观察到明显的相关性。最有可能的解释是，对于TC-MIRT来说，预先训练的概念嵌入使 θ 坐标和实际技能之间有更好的一致性。
此外，与MIRT和T-MIRT相比，TC-MIRT也显示出更好的一致性，在两个数据集上的m1和m2的值都更高。这主要是因为TC-MIRT的模型预测在很大程度上取决于概念权重 \(a_t\)，而概念权重也作为学生能力 \(θ_t\) 的正则器发挥作用，使 \(θ_t\) 的变化（在相关概念上）与之前的正确性 \(o_{t-1}\) 更加一致。

总结

本文提出了一个同时利用M2PL中的可解释参数和时间增强网络的知识状态建模能力的KT框架。具体来说，缩放门用于执行趋势预测，概念矩阵用于使项目和用户参数适应 θ 坐标，使模型能够进行概念级的弱点诊断。

在两个数据集上实验表明，TC-MIRT在性能预测和可解释性方面优于最先进的KT模型。这项工作有两个潜在的未来方向。

• 首先，学生在TC-MIRT中的能力有时会在互动之间发生剧烈变化。因此，希望利用不同类型的规律性来生成更平滑的转换。
• 其次，由于许多教育系统都是建立在现有的知识图之上的，我们将考虑使用图嵌入（而不是一个简单的概念矩阵）来带来更复杂的概念相关信息。