t-SNE算法
t-SNE 算法
前言
t-SNE(t-distributed stochastic neighbor embedding) 是用于降维的一种机器学习算法,由 Laurens van der Maaten 和 Geoffrey Hinton在 08 年提出。t-SNE 作为一种非线性降维算法,非常适用于高维数据降维到 2 维或者 3 维,便于进行可视化。在实际应用中,t-SNE 很少用于降维,主要用于可视化,可能的原因有以下几方面:
- 当发现数据需要降维时,一般是特征间存在高度的线性相关性,此时一般使用线性降维算法,比如 PCA。即使是特征之间存在非线性相关,也不会先使用非线性降维算法降维之后再搭配一个线性的模型,而是直接使用非线性模型;
- 一般 t-SNE 都将数据降到 2 维或者 3 维进行可视化,但是数据降维降的维度一般会大一些,比如需要降到 20 维,t-SNE 算法使用自由度为 1 的 t 分布很难做到好的效果,而关于如何选择自由度的问题,目前没有研究;
- t-SNE 算法的计算复杂度很高,另外它的目标函数非凸,可能会得到局部最优解;
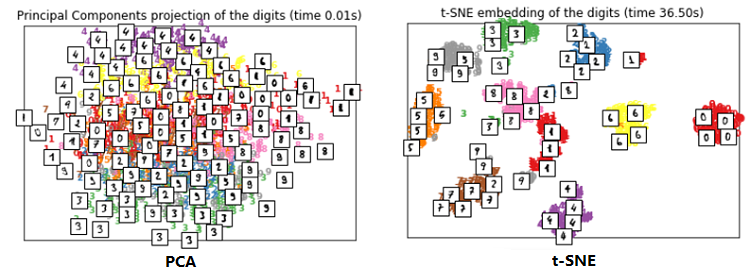
在可视化的应用中,t-SNE 的效果要好于 PCA,下面是对手写数字可视化的一个结果对比。对可视化的效果衡量,无非是两方面:相似的数据是不是离得近,不相似的数据是不是离得远。从这两方面来讲,t-SNE 的效果要明显优于 PCA。
SNE
基本思想
t-SNE 算法由 SNE 改进而来,所以先来介绍 $\mathrm{SNE}_{\circ}$ 给定 $ \mathrm{n}$ 个高维数据 $ x_{1}, x_{2}, \ldots, x_{n} $,若将其降维至 2 维,SNE 的基本思想是若两个数据在高维空间中是相似的,那么降维至 2 维空间时它们应该离得很近。
相似性计算
SNE 使用条件概率来描述两个数据之间的相似性,假设 $ x_{i}, x_{j}$ 是高维空间中的两个点,那么以点 $ x_{i}$ 为中心构建方差为 $ \sigma_{i}$ 的高斯分布,使用 $ p_{j \mid i}$ 表示 $ x_{j}$ 是 $ x_{i}$ 邻域的概率,如果 $ x_{j}$ 离 $ x_{i}$ 很近,那么 $ p_{j \mid i}$ 很大,反之, $ p_{j \mid i}$ 很小,$ p_{j \mid i}$ 定义如下:
$p_{j \mid i}=\frac{\exp \left(-\left\|x_{i}-x_{j}\right\|^{2} /\left(2 \sigma_{i}^{2}\right)\right)}{\sum_{k \neq i} \exp \left(-\left\|x_{i}-x_{k}\right\|^{2} /\left(2 \sigma_{i}^{2}\right)\right)}$
由于只关心不同点对之间的相似度,所以设定 $p_{i \mid i}=0$ 。
当把数据映射到低维空间后,高维数据点之间的相似性也应该在低维空间的数据点上体现出来。这里同样用条件概率的形式描述,假设 $ x_{i}, x_{j}$ 映射到低维空间后对应 $ y_{i}, y_{j}$,$y_{j}$ 是 $ y_{i}$ 邻域的条件概率为 $ q_{j \mid i}$ :
$q_{j \mid i}=\frac{\exp \left(-\left\|y_{i}-y_{j}\right\|^{2}\right)}{\sum \limits _{k \neq i} \exp \left(-\left\|y_{i}-y_{k}\right\|^{2}\right)}$
低维空间中的方差直接设置为 $ \sigma_{i}=\frac{1}{\sqrt{2}} $ ,方便计算,同样 $q_{i \mid i}=0$ 。
目标函数
此时就很明朗了,若 $y_{i}$ 和 $y_{j}$ 真实反映了高维数据点 $x_{i}$ 和 $x_{j}$ 之间的关系,那么条件概率 $p_{j \mid i}$ 与 $q_{j \mid} $ 应该完全相等。这里我们只考虑了 $x_{i}$ 与 $x_{j}$ 之间的条件概率,若考虑 $x_{i}$ 与其他所有点之间的条件概率,则可构成一个条件概率分布 $P_{i}$ , 同理在低维空间存在一个条件概率分布 $Q_{i}$ 且应该与 $P_{i}$ 一致。如何衡量两个分布之间的相似性? 当然是用经典的 KL 距离(Kullback-Leibler Divergence),SNE 最终目标就是对所有数据点最小化这个 KL 距 离,我们可以使用梯度下降算法最小化如下代价函数:
$C=\sum\limits_{i} K L\left(P_{i}|| Q_{i}\right)=\sum \limits _{i} \sum \limits_{j} p_{j \mid i} \log \frac{p_{j \mid i}}{q_{j \mid i}}$
似乎到这里问题就漂亮的解决了,代价函数都写出来了,剩下的事情就是利用梯度下降算法进行训练。但事情远没有那么简单,因为 KL 距离是一个非对称的度量。最小化代价函数的目的是让 $p_{j \mid i}$ 和 $q_{j \mid i}$ 的值尽可能的接近,即低维空间中点的相似性应当与高维空间中点的相似性一致。但是从代价函数的形式就可以看出,当 $p_{j \mid i}$ 较大,$q_{j \mid i}$ 较小时,代价较高;而 $p_{j \mid i}$ 较小,$ q_{j \mid i}$ 较大时,代价较低。什么意思呢? 很显然,高维空间中两个数据点距离较近时,若映射到低维空间后距离较远,那么将得到一个很高的惩罚,这当然没问题。反之,高维空间中两个数据点距离较远时,若映射到低维空间距离较近,将得到一个很低的惩罚值,这就有问题了,理应得到一个较高的惩罚才对。换句话说,SNE的代价函数更关注局部结构,而忽视了全局结构。
SNE缺点
通过以上的介绍,总结一下SNE的缺点:
- 不对称导致梯度计算复杂,对目标函数计算梯度如下,由于条件概率 $p_{j \mid i}$ 不等于 $p_{i \mid j}$,$q_{j \mid i}$ 不等于 $q_{i \mid j} $,因此梯度计算中需要的计算量较大。
$\frac{\delta C}{\delta y_{i}}=2 \sum \limits _{j}\left(p_{j \mid i}-q_{j \mid i}+p_{i \mid j}-q_{i \mid j}\right)\left(y_{i}-y_{j}\right)$
这个梯度还有一定的物理意义,我们可以用分子之间的引力和斥力进行解释。低维空间中点 $y_{i}$ 的位置是由其他所 有点对其作用力的合力所决定的。其中某个点 $y_{j}$ 对其作用力是沿着 $y_{i}-y_{j}$ 方向的,具体是引力还是斥力占主导就 取决于 $y_{j}$ 与 $y_{i}$ 之间的距离了,其实就与 $\left(p_{j \mid i}-q_{j \mid i}+p_{i \mid j}-q_{i \mid j}\right)$ 这一项有关。
- Crowing 问题。就是不同类别的簇挤在一起,无法区分开来。拥挤问题的出现与某个特定算法无关,而是由于高维空间距离分布和低维空间距离分布的差异造成的。比如有一种情况,高维度数据在降维到10维下,可以有很好的表达,但是降维到两维后无法得到可信映射,比如降维如 10 维中有 11 个点之间两两等距离的,在二维下就无法得到可信的映射结果(最多3个点)。进一步的说明,假设一个以数据点 $x_i$ 为中心,半径为 $r$ 的 $m$ 维球(三维空间就是球),其体积是按 $r^m$ 增长的,假设数据点是在m维球中均匀分布的,我们来看看其他数据点与 $x_i$ 的距离随维度增大而产生的变化。
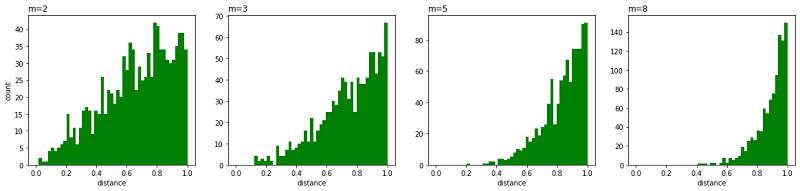
从上图可以看到,随着维度的增大,大部分数据点都聚集在 $m$ 维球的表面附近,与点 $x_i$ 的距离分布极不均衡。如果直接将这种距离关系保留到低维,就会出现拥挤问题。

import matplotlib.pyplot as plt import numpy as np from numpy.linalg import norm npoints = 1000 # 抽取1000个m维球内均匀分布的点 plt.figure(figsize=(20, 4)) for i, m in enumerate((2, 3, 5, 8)): # 这里模拟m维球中的均匀分布用到了拒绝采样,即先生成m维立方中的均匀分布,再剔除m维球外部的点 accepts = [] while len(accepts) < 1000: points = np.random.rand(500, m) accepts.extend([d for d in norm(points, axis=1) if d <= 1.0]) # 拒绝采样 accepts = accepts[:npoints] ax = plt.subplot(1, 4, i+1) ax.set_xlabel('distance') # x轴表示点到圆心的距离 if i == 0: ax.set_ylabel('count') # y轴表示点的数量 ax.hist(accepts, bins=np.linspace(0., 1., 50), color='green') ax.set_title('m={0}'.format(str(m)), loc='left') plt.show()View Code
t-SNE
SNE算法的思路是不错的,但是它的可视化效果大家也看到了,存在很大改进空间。如何改进它呢?
对称 SNE
原始 SNE 中,在高维空间中条件概率 $p_{j \mid i}$ 不等于 $p_{i \mid j}$ , 低维空间中 $q_{j \mid i}$ 不等于 $q_{i \mid j} $,于是提出对称 $\mathrm{SNE} $,采用更加通用的联合概率分布代替原始的条件概率,使得 $p_{i j}=p_{j i}, \quad q_{i j}=q_{j i} $
优化 $p_{i} \mid j$ 和 $q_{i} \mid j$ 的 KL 散度的一种替换思路是,使用联合概率分布来替换条件概率分布,即 $P$ 是高维空间里各个点的联合概率分布, $Q$ 是低维 空间下的,目标函数为:
$C=K L(P \| Q)=\sum \limits_{i} \sum \limits _{j} p_{i, j} \log \frac{p_{i j}}{q_{i j}}$
简单来讲,在低维空间中定义 $ q_{i j} $ :
$q_{i j}=\frac{\exp \left(-\left\|y_{i}-y_{j}\right\|^{2}\right)}{\sum_{k \neq l} \exp \left(-\left\|y_{k}-y_{l}\right\|^{2}\right)}$
当然,在高维空间我们也可以定义 $p_{i j} $:
$p_{i j}=\frac{\exp \left(-\left\|x_{i}-x_{j}\right\|^{2} / 2 \sigma^{2}\right)}{\sum \limits_ {k \neq l} \exp \left(-\left\|x_{k}-x_{l}\right\|^{2} / 2 \sigma^{2}\right)}$
但是在高维空间中这样的定义会带来异常值的问题,怎么理解呢? 假设点 $x_{i}$ 是一个噪声点,那么 $\left\|x_{i}-x_{j}\right\|$ 的平方会很大,那么对于所有的 $\mathrm{j}, p_{i j}$ 的值都会很小,导致在低维映射下的 $y_{i}$ 对整个损失函数的影响很小,但对于异常值,我们显然需要得到一个更大的惩罚,于是对高维空间中的联合概率修正为:
$p_{i j}=\frac{p_{i l}+p_{p_{j i}}}{2}$
这样就避免了异常值的问题,此时的梯度变为:
$\frac{\delta C}{\delta y_{i}}=4 \sum_{j}\left(p_{i j}-q_{i j}\right)\left(y_{i}-y_{j}\right)$
相比于原始 SNE,对称 SNE 的梯度更加简化,计算效率更高。但对称SNE的效果只是略微优于原始SNE的效果。
引入 t 分布
$t$-分布(t-distribution)用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知(例如在样本数量足够多时),则应该用正态分布来估计总体均值。
$t$分布曲线形态与 $n$(确切地说与自由度df)大小有关。与标准正态分布曲线相比,自由度 df 越小,$t$ 分布曲线愈平坦,曲线中间愈低,曲线双侧尾部翘得愈高;自由度 df 愈大,$t$ 分布曲线愈接近正态分布曲线,当自由度 $df=∞$ 时,$t$分布曲线为标准正态分布曲线。
假设 $X$ 服从标准正态分布 $N (0,1)$, $Y$ 服从 $ \chi^{2}(n) $分布, 那么 $Z=\frac{X}{\sqrt{Y / n}} $ 的分布称为自由度为 $n$ 的分布,记为 $Z \sim t(n) $ 。
分布密度函数 $f_{Z}(x)=\frac{\operatorname{Gam}\left(\frac{n+1}{2}\right)}{\sqrt{n \pi} \operatorname{Gam}\left(\frac{n}{2}\right)}\left(1+\frac{x^{2}}{n}\right)^{-\frac{n+1}{2}} $
其中,$ \operatorname{Gam}(\mathrm{x}) $ 为伽马函数。
对称SNE实际上在高维度下 另外一种减轻”拥挤问题”的方法:在高维空间下,在高维空间下我们使用高斯分布将距离转换为概率分布,在低维空间下,我们使用更加偏重长尾分布的方式来将距离转换为概率分布,使得高维度下中低等的距离在映射后能够有一个较大的距离。

t 分布是一种长尾分布,从图中可以看到,在没有异常点时,t 分布与高斯分布的拟合结果基本一致。而在第二张图中,出现了部分异常点,由于高斯分布的尾部较低,对异常点比较敏感,为了照顾这些异常点,高斯分布的拟合结果偏离了大多数样本所在位置,方差也较大。相比之下,t 分布的尾部较高,对异常点不敏感,保证了其鲁棒性,因此其拟合结果更为合理,较好的捕获了数据的整体特征。
那么如何利用 t 分布的长尾性来改进 SNE 呢?看下图,注意这个图并不准确,主要是为了说明 t 分布是如何发挥作用的。
图中有高斯分布和 $\mathrm{t}$ 分布两条曲线,表示点之间的相似性与距离的关系,高斯分布对应高维空间,$\mathrm{t}$ 分布对应低维空间。那么对于高维空间中相距较近的点,为了满足 $p_{i j}=q_{i j}$ , 低维空间中的距离需要稍小一点; 而对于高维空间中相距较远的点,为了满足 $p_{i j}=q_{i j} $, 低维空 间中的距离需要更远。这恰好满足了我们的需求,即同一簇内的点(距离较近)聚合的更紧密,不同簇之间的点(距离较远)更加疏远。

引入 t 分布之后,在低维空间中,用自由度为 1 的 t 分布重新定义 :
$q_{i j}=\frac{\left(1+\left\|y_{i}-y_{j}\right\|^{2}\right)^{-1}}{\sum \limits _{k \neq l}\left(1+\left\|y_{i}-y_{j}\right\|^{2}\right)^{-1}}$
然后与原始 SNE 一样,我们使用 K-L 散度定义目标函数进行优化,从而求解。至此,关于 t-SNE 算法的原理部分,我们就介绍完了。
t-SNE 算法过程
- $Data: X=x_{1}, \ldots, x_{n}$
- 计算 cost function 的参数: 困惑度 Perp
- 优化参数:设置迭代次数 $ \mathrm{T}$ , 学习速率$ \eta$ ,动量 $ \alpha(t)$
- 目标结果是低维数据表示 $ Y^{T}=y_{1}, \ldots, y_{n}$
- 开始优化 结束结束
- 计算在给定 Perp下的条件概率 $ p_{j \mid i}$ (参见上面公式)
- 令 $ p_{i j}=\frac{p_{j\left|i+p_{i}\right| j}}{2 n}$
- 用 $ N\left(0,10^{-4} I\right)$ 随机初始化 $ \mathrm{Y}$
- 迭代,从 $ \mathrm{t}=1$ 到 $ \mathrm{T}$, 做如下操作:
- 计算低维度下的 $ q_{i j}$ (参见上面的公式)
- 计算梯度(参见上面的公式)
- 更新 $ Y^{t}=Y^{t-1}+\eta \frac{d C}{d Y}+\alpha(t)\left(Y^{t-1}-Y^{t-2}\right)$
- 结束
优化过程中可以尝试的两个 trick:
- 提前压缩 (ear1y compression) : 开始初始化的时候,各个点要离得近一点。这样小的距离,方便各个聚类中心的移动。可以通过引入 $L2$ 正则项 (距离的平方和) 来实现。
- 提前夸大(ear1y exaggeration):在开始优化阶段, $ p_{i j}$ 乘以一个大于 1 的数进行扩大, 来避免因为 $ q_{i j}$ 太小导致优化太慢的问题。比如前 50 次迭代, $ p_{i j} $ 乘以 4。
优化的过程动态图如下:

不足
主要不足有四个:
- 主要用于可视化,很难用于其他目的。比如测试集合降维,因为他没有显式的预估部分,不能在测试集合直接降维;比如降维到10维,因为 t 分布偏重长尾,1个自由度的t分布很难保存好局部特征,可能需要设置成更高的自由度。
- t-SNE 倾向于保存局部特征,对于本征维数(intrinsic dimensionality)本身就很高的数据集,是不可能完整的映射到 2-3 维的空间
- t-SNE 没有唯一最优解,且没有预估部分。如果想要做预估,可以考虑降维之后,再构建一个回归方程之类的模型去做。但是要注意,t-SNE中距离本身是没有意义,都是概率分布问题。
- 训练太慢。有很多基于树的算法在 t-SNE 上做一些改进




