神奇的魔方阵–(MagicSquare)(2)
在上一篇博客中,我们讨论了阶数为奇数,以及阶数为(4K)的魔方阵的排列规则,以及代码实现(详见://www.cnblogs.com/1651472192-wz/p/14640903.html);
本篇文章则对最后一种情况: 阶数n = 4K + 2 的魔方阵 排列规律 进行分析, 以及代码实现.让我们直接进入正题:
1. 偶数阶魔方阵(n = 4*K + 2)
1.排列规律:(源自百度百科):
1. 先将整个方阵划成田字型的四个2 k + 1阶的奇数阶小方阵
2. 右半两个小方阵中大于k+2的列;
3. 左半两个小方阵中( k + 1 , k + 1 )的格位;
4. 左半两个小方阵中除了( k+1 , 1 )是指第一列第k+1行的格位之外,小于k +1的列。
5. 以奇数阶魔方阵的方法连续填制法依左上、右下、右上、左下的顺序分别填制这四个小方阵。
1.分块:
2. 按照 左上、右下、右上、左下的顺序分别以奇数魔方阵的摆放规则进行摆放 , 同时标记:
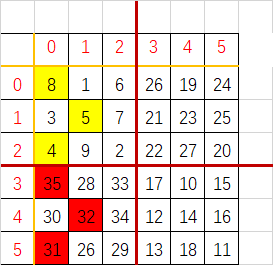
3.对标记的方块进行对调,魔方阵完成:

4.代码实现:
根据上面的分析,代码主要分为两部分 1. 分块填数, 2. 交换
代码如下:(软件:VS2019)
#include<assert.h>
#include<stdio.h>
void Print(int(*ar)[6], int row, int col)//打印 { for (int i = 0; i < row; i++) { for (int j = 0; j < col; j++) { printf("%3d", ar[i][j]); } printf("\n"); } } //传入 奇数阶小魔方阵起始的行列信息,以及小魔方阵的大小,起始的数字 void Magic_Square_1(int (*ar)[6],int row, int col, int size, int num) { assert(ar != nullptr && row >= 0 && col >= 0); ar[row][size / 2 + col] = num;//注意第一个数摆在魔方阵第row行中间的位置 // 在这里不能取col/2,要取 size/2 + col; int preRow = row;//记录上一个数字的行对于[row][col] 的偏移量 信息 int preCol = size / 2 + col; for (int i = num +1; i < num + size * size; i++) { //重点: //注意在这里行列下标都需要加上传入的row 和 col 即在这里的preRow 和 preCol 记录的是相对与 //坐标[row][col]的偏移量. if (ar[row + (preRow - 1 + size) % size][col + (preCol + 1) % size] == 0) { ar[row + (preRow - 1 + size) % size][col + (preCol + 1) % size] = i ; preRow = (preRow - 1 + size) % size; preCol = (preCol + 1) % size; } else { ar[row + (preRow + 1) % size][col + preCol] = i; preRow = (preRow + 1) % size; } } } void Swap(int* pa, int* pb) { int tmp = *pa; *pa = *pb; *pb = tmp; } void Magic_Square() { #define ROW 6 #define COL ROW int ar[ROW][COL] = {}; Magic_Square_1(ar, 0, 0, ROW / 2, 1);//左上 Magic_Square_1(ar, ROW/2, COL/2, ROW / 2, 1+(ROW*COL/4));//右下 Magic_Square_1(ar, 0, COL/2, ROW / 2, 1+ (ROW * COL / 2));//右上 Magic_Square_1(ar, ROW/2, 0, ROW / 2, 1+ (ROW * COL / 4)*3);//左下 //上下对调右半两个小方阵中大于k+2的列; for (int i = 0; i < ROW/2; i++) { for (int j = 0; j < COL; j++) { //上下对调右半两个小方阵中大于k+2的列; if (j > ((ROW - 2) / 4 + ROW/2 + 2)) // 此处 注意需要加上 ROW/2 { Swap(&ar[i][j], &ar[i + ROW / 2][j]); } //左半两个小方阵中除了( k+1 , 1 )是指第一列第k+1行的格位之外,小于k +1的列。 if(j < ((ROW - 2) / 4 ) ) //此处注意在程序中,下标是从零开始的,所以不需要加1 即:if(j < ((ROW - 2) / 4 + 1)) 这样是错误的 { if (j != 1 && i != ((ROW - 2) / 4 ))//同上不需要加一 { Swap(&ar[i][j], &ar[i + ROW / 2][j]); } } } } //左半两个小方阵中( k + 1 , k + 1 )的格位; Swap(&ar[ROW / 4][COL / 4], &ar[ROW / 4 + ROW / 2][COL / 4]); Print(ar, ROW, COL); #undef ROW #undef COL } int main() { Magic_Square(); return 0; }
运行结果:
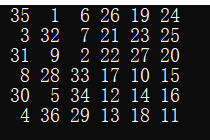
(若有大哥发现其中的不合适或者错误,请务必在评论中告知,小弟在这里祝大哥心情愉悦,生活快乐!)
本篇完.

