手写堆
- 2019 年 10 月 3 日
- 筆記
堆
1.定义
堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。
2.性质
1.堆中某个节点的值总是不大于或不小于其父节点的值;
2.堆总是一棵完全二叉树。
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
堆是非线性数据结构,相当于一维数组,有两个直接后继。
3.应用思路(手写堆)
以最小堆为例
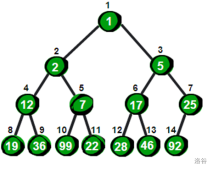

先把数组中的数储存起来
很显然最小的数就在堆顶,假设存储这个堆的数组叫做h的话,最小数就是h[1]。接下来,我们将堆顶的数删除,并将新增加的数23放到堆顶。显然加了新数后已经不符合最小堆的特性,我们需要将新增加的数调整到合适的位置。那如何调整呢?
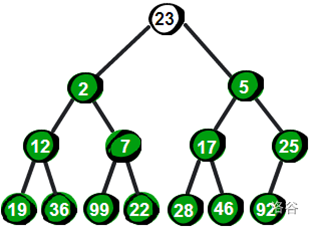
我们可以将它和它的两个儿子进行比较,将儿子小的置为堆顶即可,然后依次下调
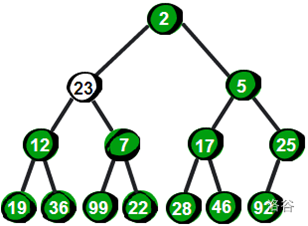
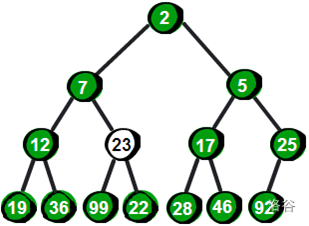
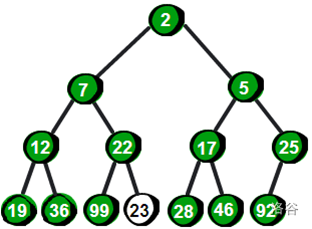
那如果是要新添加一个数,又如何操作呢?
同前面的,我们可以将新的点加到堆尾,然后上调与它的父节点比较即可。
代码
堆的操作(以大根堆为例)
关于小根堆的操作放在了文章后面。
1.堆的元素下调
void shiftdownmax(int x){ int t,flag=0; while(x*2<=addmax&&flag==0){ if(maxn[x]<maxn[x*2])t=x*2; else t=x; if(x*2+1<=addmax){ if(maxn[t]<maxn[x*2+1])t=x*2+1; } if(t!=x){ swap(maxn[t],maxn[x]); x=t; }else flag=1; } }2.堆的元素上调
void shiftdownmax(int x){ int t,flag=0; while(x*2<=addmax&&flag==0){ if(maxn[x]<maxn[x*2])t=x*2; else t=x; if(x*2+1<=addmax){ if(maxn[t]<maxn[x*2+1])t=x*2+1; } if(t!=x){ swap(maxn[t],maxn[x]); x=t; }else flag=1; } }3.建堆
由于堆的性质,只要调整一半的元素即可。
for(int i=1;i<=n;++i){ addmax++; maxn[addmax]=a[i]; } for(int i=addmax/2;i>=1;--i){ shiftdownmax(i); }4.取出元素
取出第一个元素将最后一个元素放在第一个元素的位置,并且元素个数减1,对堆顶进行下调操作。
int y=maxn[1]; maxn[1]=maxn[addmax--]; shiftdownmax(1);5.加入元素
在堆尾加入新元素并且对其进行上调操作
maxn[++addmax]=x; shiftupmax(addmax);4.例题
合并果子
题意
在一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。
每一次合并,多多可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。可以看出,所有的果子经过n-1次合并之后,就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使多多耗费的体力最少,并输出这个最小的体力耗费值。
例如有3种果子,数目依次为1,2,9。可以先将1、2堆合并,新堆数目为3,耗费体力为3。接着,将新堆与原先的第三堆合并,又得到新的堆,数目为12,耗费体力为12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。
思路阐述
堆的入门题,我们只要建立一个最小堆,然后依次取出堆顶2次,将其合并之后再放入堆中即可。
代码实现
#include <cstdio> #include <cmath> #include <iostream> using namespace std; int n,a[100005],add,p,q,sum,ans=0; void shiftdown(int x){ int t,flag=0; while(x*2<=add && flag==0){ if(a[x]>a[x*2])t=x*2; else t=x; if(x*2+1<=add){ if(a[t]>a[x*2+1])t=x*2+1; } if(t!=x){ swap(a[t],a[x]); x=t; }else flag=1; } } int main(){ scanf("%d",&n); add=n; for(int i=1;i<=n;++i){ scanf("%d",&a[i]); } for(int i=n/2;i>=1;i--){ shiftdown(i); } for(int i=1;i<=n-1;++i){ p=a[1]; a[1]=a[add]; add--; shiftdown(1); q=a[1]; sum=q+p; a[1]=sum; shiftdown(1); ans=ans+sum; } printf("%d",ans); return 0; }5.习题
6.关于堆的一些操作
1.小根堆向下调整
void shiftdownmin(int x){ int t,flag=0; while(x*2<=addmin&&flag==0){ if(minn[x]>minn[x*2])t=x*2; else t=x; if(x*2+1<=addmin){ if(minn[t]>minn[x*2+1])t=x*2+1; } if(t!=x){ swap(minn[t],minn[x]); x=t; }else flag=1; } }2.小根堆向上调整
void shiftupmin(int x) { int flag=0; if(x==1) return; while(x!=1 && flag==0){ if(minn[x]<minn[x/2]) swap(minn[x],minn[x/2]); else flag=1; x=x/2; } }3.大根堆向下调整
void shiftdownmax(int x){ int t,flag=0; while(x*2<=addmax&&flag==0){ if(maxn[x]<maxn[x*2])t=x*2; else t=x; if(x*2+1<=addmax){ if(maxn[t]<maxn[x*2+1])t=x*2+1; } if(t!=x){ swap(maxn[t],maxn[x]); x=t; }else flag=1; } }4.大根堆向上调整
void shiftupmax(int x) { int flag=0; if(x==1) return; while(x!=1&&flag==0){ if(maxn[x]>maxn[x/2]) swap(maxn[x],maxn[x/2]); else flag=1; x=x/2; } }