keras下的self attention和一些总结与思考

2020 年 12 月 23 日
AI

还是回顾一下经典的原论文《attention is all you need》

前面关于RNN和CNN的论述不写了，有几个地方需要注意：

1、RNN的加速方案：

Oleksii Kuchaiev and Boris Ginsburg. Factorization tricks for LSTM networks. arXiv preprint arXiv:1703.10722, 2017.

[32] Noam Shazeer, Azalia Mirhoseini, Krzysztof Maziarz, Andy Davis, Quoc Le, Geoffrey Hinton, and Jeff Dean. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. arXiv preprint arXiv:1701.06538, 2017.

新智元：比RNN快136倍！上交大提出SRNN，能做并行计算zhuanlan.zhihu.com

然而，RNN顺序计算的基本约束仍然存在。

2、减少RNN的顺序计算的复杂度的目标也催生了 Extended Neural GPU , ByteNet 和 ConvS2S，所有这些都是使用卷积神经网络作为基本构建块，并行地计算所有输入和输出位置的隐藏表示。在这些模型中，将来自两个任意输入或输出位置的信号关联起来所需的参数量随着位置的距离而增长，对于ConvS2S是线性增长的，对于ByteNet则是对数增长的。这使得学习远程位置之间的依赖关系变得更加困难，因为参数量太大实际上又提高了复杂度。在transformer中，这被减少到恒定数量的操作，尽管代价是由于平均注意加权的位置而降低了模型的有效性，这一效果通过使用多头注意力机制抵消，如第3.2节所述。

前面基本介绍了rnn和cnn在机器翻译这类应用的后续的一些发展balabala，然后这里交代了为啥使用多头注意力机制，简单来说就是提高模型的表达能力，毕竟多头的参数增加了那么多的。。。

然后就直接给了这个图。。。

这里需要补充一下self attention的基本知识，这个论文的后面一个小节就写的很清楚，这里把attention机制概括为 query key 和value，query和key进行score相似度计算得到attention weights，然后attention weights和key加权求和得到最终的attention vector，

马东什么：keras的几种attention layer的实现之一zhuanlan.zhihu.com

这个其实放到之前的几种attention机制里也是可以这么概括的，但是只能说是概括了。。因为并不是完全一致的。。。比如说：

BahdanauAttention attention和 Luongs’ attention

query就是encode的rnn的最后一个时间步输出的hidden state（也是decoder的初始时间步）和decoder的rnn中的每一个时间步输出的hidden state，key=value（最常见的情况），key是encoder中的rnn的每一个时间步输出的hidden state，这里key和query进行score相似度计算经过softmax得到attention weights，然后attention weights和value（也就是和key）进行加权求和计算。

但是不同的机制在实现的细节上还是有一些小区别的，比如上面的图片中还包含了将经过attention weights加权求和之后的context vector和原始的decoder的每一个hidden state分别进行concat然后再经过一个dense层然后再tanh激活的过程。

也就是说q、v、k这个说法概括了各类attention机制的核心步骤但并不是所有步骤的。

比如文中提到的attention layer的结构：

这个地方就很好理解，q和k相似度计算然后通过scale（scale不影响理解就是要给放缩系数，避免q和k的一些相似度计算，比如点积得到太大的结果），然后经过一个mask层再经过softmax得到attention weights然后和value（大部分情况下value=key）进行加权求和计算。

这个地方有一些细节，也是面试可能会问到的部分：

transformer中的attention为什么scaled?www.zhihu.com

1、为什么要引入scale这个参数（这个参数在之前文章里提到的attention机制中都莫得）？

这个答案真的写的太好了，理论+例子+代码，完美！

scale避免了softmax计算太大的点积的时候将几乎全部的概率分布分配给最大值对应的标签，避免了反向传播过程中梯度消失为0的问题；

另外第二高赞的回答也很好，

点积相似性因为使用了矩阵乘法可能会出现点积结果太大的问题，而求和相似性则没有这样的问题，毕竟100+100=200，100*100=10000，已经是量级的差距了。

另外给了论文中的部分内容：

这里的dk表示的是attention计算的时候向量的维度。

然后是第二个问题

维度与点积大小的关系是怎么样的，为什么使用维度的根号来放缩？

假设向量 $q$ 和 $k$ 的各个分量是互相独立的随机变量，均值是0，方差是1，那么点积 $q\cdot k$ 的均值是0，方差是 $d_k$ 。

方差越大也就说明，点积的数量级越大（以越大的概率取到很大的值）。那么一个自然的做法就是把方差稳定到1，做法是将点积除以 $\sqrt d_k$ ，这样有：

将方差控制为1，也就有效地控制了前面提到的梯度消失的问题。

扯多了，回到刚才的问题上，我们提到瑟利夫attention的公式如上，其实去掉scaled的话形式上就是常规的attention的形式，self attention只是在q v k上的取值不同，大部分情况下，key=value！=query，而在self attention中key=value=query

看一下git上的一些高star的keras的self attention机制的实现

//github.com/CyberZHG/keras-self-attention/tree/master/keras_self_attentiongithub.com

Python">from .backend import keras
from .backend import backend as K


class ScaledDotProductAttention(keras.layers.Layer):
    r"""The attention layer that takes three inputs representing queries, keys and values.
    \text{Attention}(Q, K, V) = \text{softmax}(\frac{Q K^T}{\sqrt{d_k}}) V
    See: //arxiv.org/pdf/1706.03762.pdf
    """

    def __init__(self,
                 return_attention=False,
                 history_only=False,
                 **kwargs):
        """Initialize the layer.
        :param return_attention: Whether to return attention weights.
        :param history_only: Whether to only use history data.
        :param kwargs: Arguments for parent class.
        """
        super(ScaledDotProductAttention, self).__init__(**kwargs)
        self.supports_masking = True
        self.return_attention = return_attention
        self.history_only = history_only
        self.intensity = self.attention = None

    def get_config(self):
        config = {
            'return_attention': self.return_attention,
            'history_only': self.history_only,
        }
        base_config = super(ScaledDotProductAttention, self).get_config()
        return dict(list(base_config.items()) + list(config.items()))

    def compute_output_shape(self, input_shape):
        if isinstance(input_shape, list):
            query_shape, key_shape, value_shape = input_shape
        else:
            query_shape = key_shape = value_shape = input_shape
        output_shape = query_shape[:-1] + value_shape[-1:]
        if self.return_attention:
            attention_shape = query_shape[:2] + (key_shape[1],)
            return [output_shape, attention_shape]
        return output_shape

    def compute_mask(self, inputs, mask=None):
        if isinstance(mask, list):
            mask = mask[0]
        if self.return_attention:
            return [mask, None]
        return mask

    def call(self, inputs, mask=None, **kwargs):
        if isinstance(inputs, list):
            query, key, value = inputs
        else:
            query = key = value = inputs
        if isinstance(mask, list):
            mask = mask[1]
        feature_dim = K.shape(query)[-1]
        e = K.batch_dot(query, key, axes=2) / K.sqrt(K.cast(feature_dim, dtype=K.floatx()))
        if self.history_only:
            query_len, key_len = K.shape(query)[1], K.shape(key)[1]
            indices = K.expand_dims(K.arange(0, key_len), axis=0)
            upper = K.expand_dims(K.arange(0, query_len), axis=-1)
            e -= 10000.0 * K.expand_dims(K.cast(indices > upper, K.floatx()), axis=0)
        if mask is not None:
            e -= 10000.0 * (1.0 - K.cast(K.expand_dims(mask, axis=-2), K.floatx()))
        self.intensity = e
        e = K.exp(e - K.max(e, axis=-1, keepdims=True))
        self.attention = e / K.sum(e, axis=-1, keepdims=True)
        v = K.batch_dot(self.attention, value)
        if self.return_attention:
            return [v, self.attention]
        return v

注意，这里ScaledDotProductAttention这个类实现的是点积相似性，和self attention没有关系，如果要使得上述的attention变成self attention，仅仅令query=key=value就可以了。。。

这里的scale对点积结果的规约发生在这里：

e = K.batch_dot(query, key, axes=2) / K.sqrt(K.cast(feature_dim, dtype=K.floatx()))

        if self.history_only:
            query_len, key_len = K.shape(query)[1], K.shape(key)[1]
            indices = K.expand_dims(K.arange(0, key_len), axis=0)
            upper = K.expand_dims(K.arange(0, query_len), axis=-1)
            e -= 10000.0 * K.expand_dims(K.cast(indices > upper, K.floatx()), axis=0)

这部分其实我没太明白是在干啥，代码实现上是截取key超过query的部分。。。

e -= 10000.0 * (1.0 - K.cast(K.expand_dims(mask, axis=-2), K.floatx()))

然后是关于mask的部分，关于mask层的作用：

马东什么：关于mask层zhuanlan.zhihu.com

这里实际上在做的就是

也就是下面这部分代码在做的事情

        if mask is not None:
            e -= 10000.0 * (1.0 - K.cast(K.expand_dims(mask, axis=-2), K.floatx()))
        self.intensity = e
        e = K.exp(e - K.max(e, axis=-1, keepdims=True))
        self.attention = e / K.sum(e, axis=-1, keepdims=True)

假设mask层e=[0 0 0 1 1 1]

则 10000.0 * (1.0 – K.cast(K.expand_dims(mask, axis=-2), K.floatx()))的结果为 10000*[1 1 1 0 0 0]=[10000,10000,10000,0 0 0 ]，然后用e=[0 0 0 1 1 1]-[10000,10000,10000,0 0 0 ]=[-10000,-10000,-10000,1,1,1]，然后是：

e = K.exp(e – K.max(e, axis=-1, keepdims=True))

也就是 [-10000,-10000,-10000,1,1,1]-max([-10000,-10000,-10000,1,1,1])=[-10000,-10000,-10000,1,1,1]-1=[-10001,-10001,-10001,0,0,0]

然后取exp得到 [e**-10001,e**-10001,e**-10001,1,1,1]约等于[0,0,0,1,1,1]，这样就把padding的部分在softmax计算之前处理掉从而不会影响后续softmax的计算了。

然后需要注意的就是我们平常使用embedding层是一般默认是不进行mask处理的：

keras.layers.Embedding(input_dim, output_dim, 
                           embeddings_initializer='uniform', 
                           embeddings_regularizer=None, 
                           activity_regularizer=None, 
                           embeddings_constraint=None,
                           mask_zero=False, 
                           input_length=None)

mask_zero：布尔值，确定是否将输入中的‘0’看作是应该被忽略的‘填充’（padding）值，该参数在使用递归层处理变长输入时有用。设置为True的话，模型中后续的层必须都支持masking，否则会抛出异常。如果该值为True，则下标0在字典中不可用，input_dim应设置为|vocabulary| + 1。

我们平常在进行文本分类之类的任务的时候基本没有处理这个东西，因为很多时候我们直接把填充词 0 作为一项有效的输入，也就是embedding矩阵里面会针对“0”这个词单独列一行出来处理0，并且这一行也会得到训练，主要是因为如果让embedding层进行mask，则后续的的一些layer要支持mask层（

在tf.keras中，lstm可以直接支持embedding的mask

inputs = keras.Input(shape=(None,), dtype="int32")
x = layers.Embedding(input_dim=5000, output_dim=16, mask_zero=True)(inputs)
outputs = layers.LSTM(32)(x)

model = keras.Model(inputs, outputs)

），这在实现上非常的麻烦，因为我们需要针对于后续的层重新进行mask的支持和设计。

在时间序列的问题里比较少遇到padding补0的问题，所以时间序列预测了关于mask的论述很少。

这里就对transofrmer的self attention的部分理解完毕了，看起来好像挺简单的。。。

然后是关于multi-head的部分：

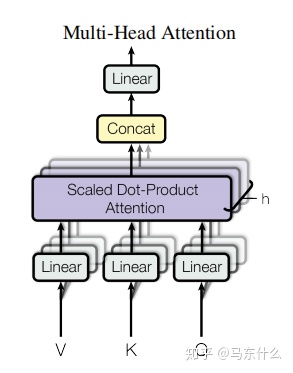
首先就是multi head本身不是什么新的东西：

//github.com/CyberZHG/keras-multi-headgithub.com

这几个都是同一个作者写的。。简直棒呆

所谓的multi head所做的事情就是上图这样的一个包装过程，对于常规的layer也可以使用multi head来增强其表达能力：

import keras
from keras_multi_head import MultiHead


model = keras.models.Sequential()
model.add(keras.layers.Embedding(input_dim=100, output_dim=20, name='Embedding'))
model.add(MultiHead(keras.layers.LSTM(units=32), layer_num=5, name='Multi-LSTMs'))
model.add(keras.layers.Flatten(name='Flatten'))
model.add(keras.layers.Dense(units=4, activation='softmax', name='Dense'))
model.build()
model.summary()

我们常常提到所谓的多输入和多输出网络，这里比较类似，不过不是针对于输入和输出的多少而是针对于网络中的某一些层的下一步输出来定义多少，这样的话，每一个head的参数和其它head独立，比如本来是使用一个LSTM，参数量假设是10000，使用multihead的结构，假设我们multi 5个head，则参数量为50000，参数量大大增加，模型的表达能力更强（我尝试过大概在1000万的量级使用multi head的lstm来进行时间序列预测，有两个问题，参数量太大了，服务器跑不动，另一个问题是loss几个epochs就非常小了，但是val的loss很大，过拟合问题严重）

所以multi head也很好理解，至于为什么使用multi head：

休息休息。。。未完待续

keras下的self attention和一些总结与思考

VirMach 便宜 VPS

QNews

keras下的self attention和一些总结与思考

分享此文：

Related Posts

主成分分析|机器学习推导系列（五）

小鱼的碎碎念

首款商用的透明电视！小米高端旗舰电视惊艳到老外

关于mask层

VirMach 便宜 VPS

QNews

熱門搜尋