在一个树型结构数据中,查找相邻有相同属性的节点的最大数量的方法
- 2019 年 10 月 3 日
- 筆記
本文介绍的是一个在一个树型数据结构中,查找 type 属性均为 a 的相邻节点的最长链路的节点数量,如果中间有任何其他节点插在其中,那这个长度就结束了,必须是相邻的。一个最简单的示例就是在一个树型结构中,有两个节点要进行连接,但是连接的节点如果都是 type 为 a 的话,则最长不能超过5个,超过五个则节点不能进行连接。
如下图:
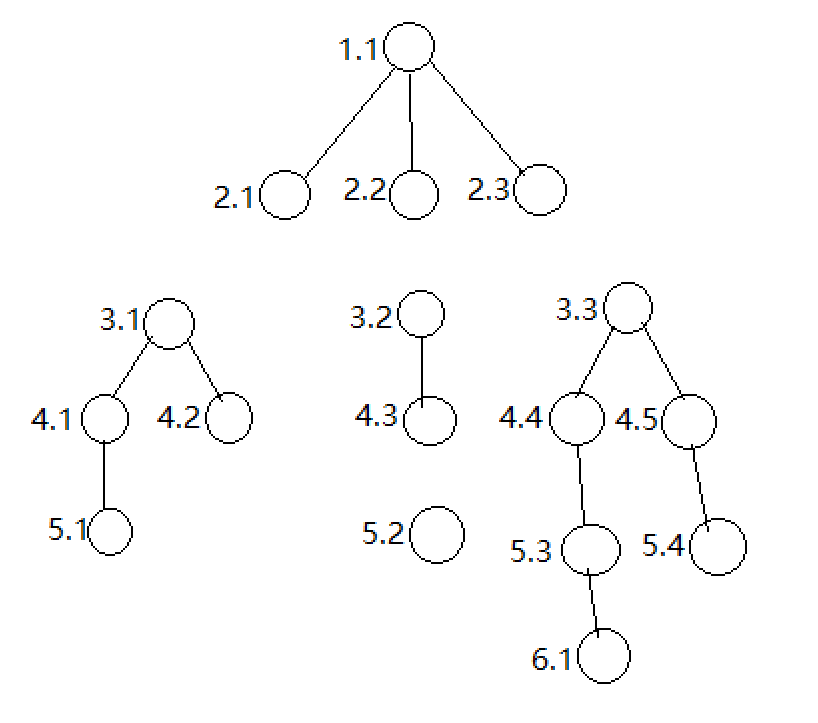
在进行节点之间的连接时,如过相邻的节点 type 属性均为 a 的超过五个就不能连接。假设上图的节点都有 type 属性,且都为 a ,则在连接时 2.1 节点是可以和 3.1 节点连接的,而 2.3 是不能和 3.3 进行连接的,因为连接后,最长的到了 6.1 节点,长度超过了 5 个。5.1后面也不能来连接其他 type 为 a 的节点了。那要怎么判断在进行连接时这个长度是否超过 5 个,这就是本文要介绍的内容,一个算法,但是是有前提条件的。
首先这些节点上要有这些信息:这个节点的 ID、它父节点的 ID、它子节点的 ID;每个节点都有 type 属性,标记这个节点是什么节点;有方法可以获取所有节点的信息,方便通过 ID 进行查询。
有人会说,那该怎么获取所有节点的信息呢?其实只要在创建时,把节点的信息保存在一个对象中即可,以 ID 作为 key,以其信息作为 key值;
如下对象中表示:
const nodes = { ... //还有其他节点信息 id21: { nodeId: id21, type: 'a', parentNodeIds: { id11: true, id12: true, }, childNodeIds: { id31: true, id32: true, }, }, ... //还有其他节点信息 }
nodes 里保存着在创建时每个节点的一些信息,在有改动(连线、断开连线、删除)操作时,同时进行数据的修改,则可以通过 nodes 来很方便的获得所有节点的连接信息、type 信息及其他保存在其中的信息。之后再连接节点时候就可以直接获取到节点的 type 类型了。
只有查找相邻的 type 属性均为某一值的节点总数的时侯才能用这个方法,当然,查找的思路也可以用到别的地方,看各位的脑洞了。
先说下思路,在连接时,我们可以先判断所连接的两个节点是不是都是 type 为 a,只有都是为 a 的情况下,才有进行后续计算的必要;之后分为向上查询所连接的相邻的 type 为 a 的节点组成的最长链路层数是几;还有就是向下查询所连接的相邻的 type 为 a 的节点组成的最长链路层数是几;之后通过这两个值来判断长度是否有超过 5 个。这就是进行编写代码的一个思路了。
向上与向下查询所用的思路是一样的,都是先查找该节点的所有子节点的类型 type,将 type 为 a 的节点 ID 记录一下,再将这些子节点的所有子节点都取出来,以作下次运算。这里要用到递归了,递归的结束条件就是子节点的 type 类型没有一个是 a,则递归结束了。
直接上伪代码:
function statisticalNodeNumber(node1, node2) { const type1 = node1.type; const type2 = node2.type; if (type1 === 'a' && type2 === 'a') { const beforeNum = statisticalBeforeNodeNumber([node1.nodeId], 0); const nextNum = statisticalNextNodeNumber([node2.nodeId], 0); return beforeNum + nextNum > 5; } } function statisticalNextNodeNumber(nodeIds, num) { let total = num; let nodeTypeIsA = []; let childNodeIds = []; const nodes = nodes; // 获取所有节点信息的方法或对象 nodeIds.forEach((val) => { const type = nodes[val].type; if (type === 'a') { // 如果type为a的话,则保存到数组 nodeTypeIsA 中,之后判断数组 nodeTypeIsA 是否长度为0 // 如果不为0则表示这一层级中有节点 type 为 a,则总数可加一,再取出所有type为a的节点的子 // 节点进行下一轮计算,直到该层级中没有 type 为 a 的节点为止 nodeTypeIsA.push(val); const n = nodes[val].childNodeIds ? Object.keys(nodes[val].childNodeIds) : []; childNodeIds = [...childNodeIds, ...n]; } }); if (nodeTypeIsA.length === 0) { return total; } ++total; return statisticalNextNodeNumber(childNodeIds, total); } function statisticalBeforeNodeNumber(nodeIds, num) { let total = num; let nodeTypeIsA = []; let beforeNodeIds = []; const nodes = nodes; // 获取所有节点信息的方法或对象 nodeIds.forEach((val) => { const type = nodes[val].type; if (type === 'a') { nodeTypeIsA.push(val); const n = nodes[val].parentNodeIds ? Object.keys(nodes[val].parentNodeIds) : []; beforeNodeIds = [...beforeNodeIds, ...n]; } }); if (nodeTypeIsA.length === 0) { return total; } ++total; return statisticalNextNodeNumber(beforeNodeIds, total); }
上面两个函数最重要想法就是按照层级去查找,只有该层级中有 type 为 a 时,则数量加 1,并只对 type 为 a 的节点的子节点进行后续的计算。所以就可以查出在两个节点相连时,相邻的节点type为a的最长数量是多少。
以上就是这次分享的内容,希望对大家有所帮助。
