python机器学习——随机梯度下降
- 2019 年 11 月 13 日
- 筆記
上一篇我们实现了使用梯度下降法的自适应线性神经元,这个方法会使用所有的训练样本来对权重向量进行更新,也可以称之为批量梯度下降(batch gradient descent)。假设现在我们数据集中拥有大量的样本,比如百万条样本,那么如果我们现在使用批量梯度下降来训练模型,每更新一次权重向量,我们都要使用百万条样本,训练时间很长,效率很低,我们能不能找到一种方法,既能使用梯度下降法,但是又不要每次更新权重都要使用到所有的样本,于是随机梯度下降法(stochastic gradient descent)便被提出来了。
随机梯度下降法可以只用一个训练样本来对权重向量进行更新:
[ eta(y^i-phi(z^i))x^i ]
这种方法比批量梯度下降法收敛的更快,因为它可以更加频繁的更新权重向量,并且使用当个样本来更新权重,相比于使用全部的样本来更新更具有随机性,有助于算法避免陷入到局部最小值,使用这个方法的要注意在选取样本进行更新时一定要随机选取,每次迭代前都要打乱所有的样本顺序,保证训练的随机性,并且在训练时的学习率也不是固定不变的,可以随着迭代次数的增加,学习率逐渐减小,这种方法可以有助于算法收敛。
现在我们有了使用全部样本的批量梯度下降法,也有了使用单个样本的随机梯度下降法,那么一种折中的方法,称为最小批学习(mini-batch learning),它每次使用一部分训练样本来更新权重向量。
接下来我们实现使用随机梯度下降法的Adaline
from numpy.random import seedclass AdalineSGD(object): """ADAptive LInear NEuron classifier. Parameters ---------- eta:float Learning rate(between 0.0 and 1.0 n_iter:int Passes over the training dataset. Attributes ---------- w_: 1d-array weights after fitting. errors_: list Number of miscalssifications in every epoch. shuffle:bool(default: True) Shuffle training data every epoch if True to prevent cycles. random_state: int(default: None) Set random state for shuffling and initalizing the weights. """ def __init__(self, eta=0.01, n_iter=10, shuffle=True, random_state=None): self.eta = eta self.n_iter = n_iter self.w_initialized = False self.shuffle = shuffle if random_state: seed(random_state) def fit(self, X, y): """Fit training data. :param X:{array-like}, shape=[n_samples, n_features] :param y: array-like, shape=[n_samples] :return: self:object """ self._initialize_weights(X.shape[1]) self.cost_ = [] for i in range(self.n_iter): if self.shuffle: X, y = self._shuffle(X, y) cost = [] for xi, target in zip(X, y): cost.append(self._update_weights(xi, target)) avg_cost = sum(cost)/len(y) self.cost_.append(avg_cost) return self def partial_fit(self, X, y): """Fit training data without reinitializing the weights.""" if not self.w_initialized: self._initialize_weights(X.shape[1]) if y.ravel().shape[0] > 1: for xi, target in zip(X, y): self._update_weights(xi, target) else: self._update_weights(X, y) return self def _shuffle(self, X, y): """Shuffle training data""" r = np.random.permutation(len(y)) return X[r], y[r] def _initialize_weights(self, m): """Initialize weights to zeros""" self.w_ = np.zeros(1 + m) self.w_initialized = True def _update_weights(self, xi, target): """Apply Adaline learning rule to update the weights""" output = self.net_input(xi) error = (target - output) self.w_[1:] += self.eta * xi.dot(error) self.w_[0] += self.eta * error cost = 0.5 * error ** 2 return cost def net_input(self, X): """Calculate net input""" return np.dot(X, self.w_[1:]) + self.w_[0] def activation(self, X): """Computer linear activation""" return self.net_input(X) def predict(self, X): """Return class label after unit step""" return np.where(self.activation(X) >= 0.0, 1, -1) 其中_shuffle方法中,调用numpy.random中的permutation函数得到0-100的一个随机序列,然后这个序列作为特征矩阵和类别向量的下标,就可以起到打乱样本顺序的功能。
现在开始训练
ada = AdalineSGD(n_iter=15, eta=0.01, random_state=1) ada.fit(X_std, y)画出分界图和训练曲线图
plot_decision_region(X_std, y, classifier=ada) plt.title('Adaline - Stochastic Gradient Desent') plt.xlabel('sepal length [standardized]') plt.ylabel('petal length [standardized]') plt.legend(loc = 'upper left') plt.show() plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o') plt.xlabel('Epochs') plt.ylabel('Average Cost') plt.show()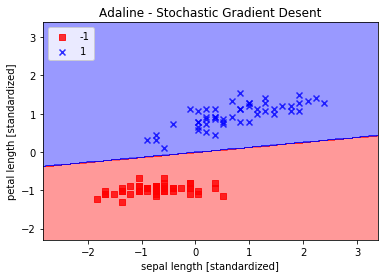

从上图可以看出,平均损失下降很快,在大概第15次迭代后,分界线和使用批量梯度下降的Adaline分界线很类似。


