浅谈神经网络中的激活函数

• 2019 年 10 月 3 日
• 筆記

       激活函数是神经网络中一个重要的环节，本文将介绍为什么神经网络网络要利用激活函数，几种常用的激活函数(逻辑函数Sigmoid、双曲正切函数tanh、线性整流函数(ReLU)，神经网络中的梯度消失问题和ReLU如何避免梯度消失。

1 用激活函数的原因

       如果神经网络没有进行可以提取非线性特征的卷积操作，而且该神经网络也不用激活函数，那么这个神经网络第i层输出只有Wxi+b。这样此神经网络不论有多少层，第i层的输出都是一个关于第i层输入xi的线性组合，相当于此时多层神经网络退化为一个多层的线性回归模型，难以学习如图像、音频、文本等复杂数据的特征。

       正因为这个原因，神经网络要引入激活函数来给神经网络增加一些非线性的特性，所以目前常见的激活函数大多是非线性函数。这样神经网络中下一层得到的输入不再是线性组合了。

2 常见的激活函数

2.1 逻辑函数Sigmoid [1]

       逻辑函数（logistic function）或逻辑曲线（logistic curve）是一种常见的S函数，它是皮埃尔·弗朗索瓦·韦吕勒在1844或1845年在研究它与人口增长的关系时命名的。

       一个简单的Logistic函数表达式为:

[ fleft( x right) = frac{1}{{1 + {e^{ – x}}}} ]

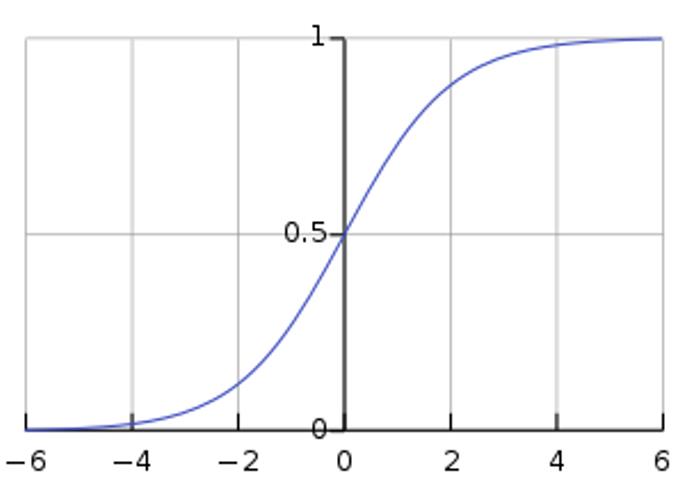
图1 标准逻辑函数的图像

       逻辑函数形如S，所以通常也叫做S形函数。

       从函数图像易知f(x)的定义域为[-∞, +∞]， 值域是(0,1)

       对f(x)求导数，易得

[f'left( x right) = {left( {frac{1}{{1 + {e^{ – x}}}}} right)^prime } = frac{{{e^{ – x}}}}{{{{left( {1 + {e^{ – x}}} right)}^2}}};; = fleft( x right)left( {1 – fleft( x right)} right)]

2.2 双曲正切函数tanh [2]

       双曲正切函数是双曲函数的一种。在数学中，双曲函数是一类与常见的三角函数类似的函数。双曲正切函数的定义为

[fleft( x right) = tanh left( x right) = frac{{{e^x} – {e^{ – x}}}}{{{e^x} + {e^{ – x}}}}]

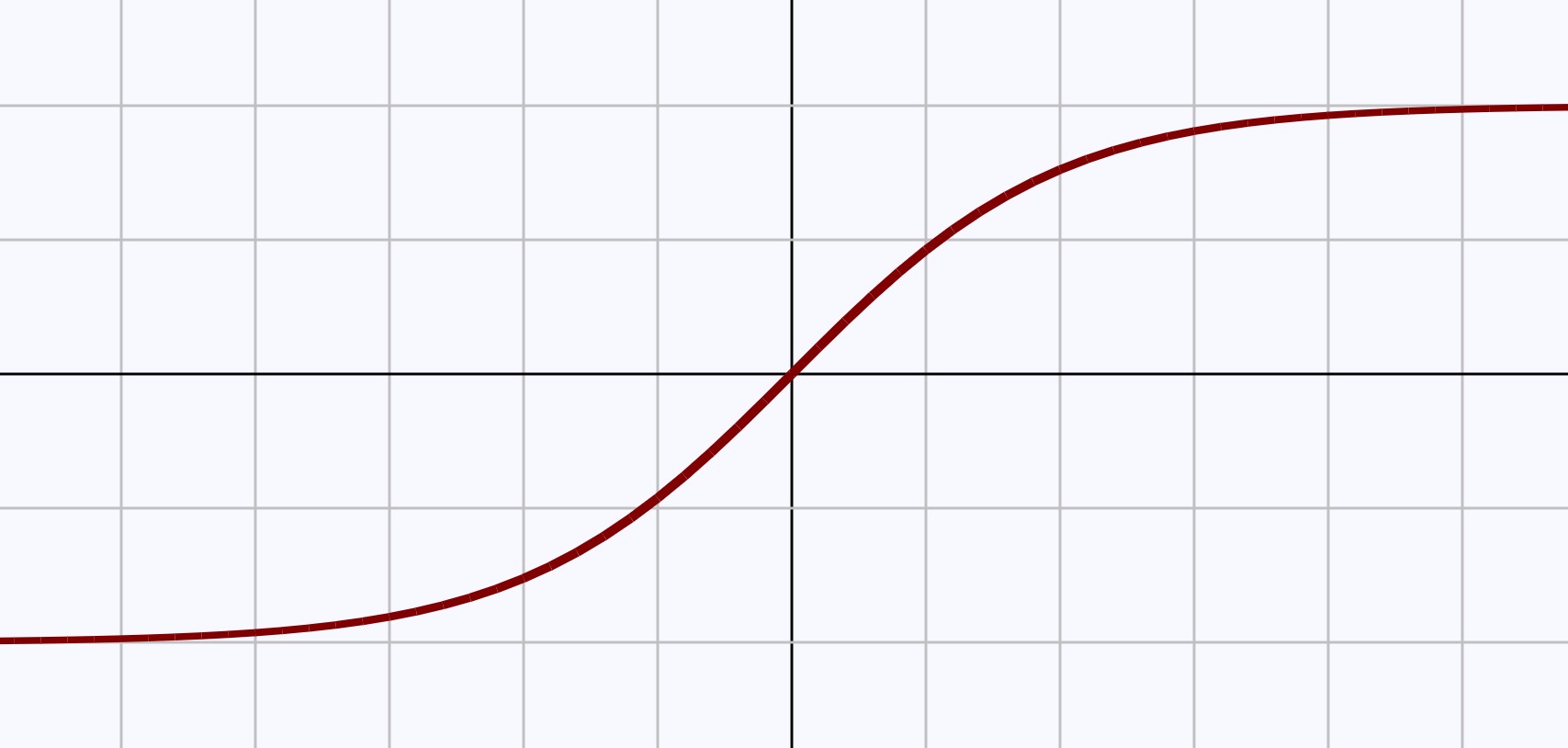
图2 双曲正切函数的图像（同逻辑函数类似）

       从函数图像易知f(x)的定义域为[-∞, +∞]， 值域是(-1,1)

       对f(x)求导数，易得

[f'left( x right) = {left( {frac{{{e^x} – {e^{ – x}}}}{{{e^x} + {e^{ – x}}}}} right)^prime } = frac{4}{{{{left( {{e^x} + {e^{ – x}}} right)}^2}}};; = 1 – f{left( x right)^2}]

2.3 线性整流函数ReLU [3]

       线性整流函数（Rectified Linear Unit, ReLU）,又称修正线性单元, 是一种人工神经网络中常用的激活函数，通常指代以斜坡函数及其变种为代表的非线性函数。

       通常意义下，线性整流函数指代数学中的斜坡函数，即

[fleft( x right) = left{ begin{array}{l} xquad quad x ge 0 \ 0quad quad x < 0 \ end{array} right.]

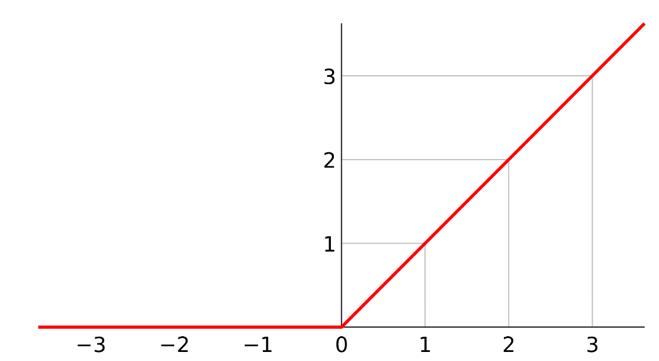
图3 ReLU函数图像

       从函数图像易知f(x)的定义域为[-∞, +∞]， 值域是[0, +∞)

       对f(x)求导数，易得

[f'left( x right) = left{ begin{array}{l} 1quad quad x ge 0 \ 0quad quad x < 0 \ end{array} right.]

3 梯度消失问题和ReLU如何处理此问题

       使用S形函数作为激活的神经网络中，随着神经网络的层数增加，神经网络后面层在梯度下降中求导的梯度几乎为0，从而导致神经网络网络后面层的权值矩阵几乎无法更新。表现为随着隐藏层数目的增加，分类准确率反而下降了。这种现象叫做消失的梯度问题。

       假设神经网络只有三层，用S型函数作为激活函数

       第一层输入为x, 输出为S(W1x+b1)

       第二层输入为S(W1x+b1)，输出为S(W2S(W1x+b1)+b2)

       第三层输入为S(W2S(W1x+b1)+b2)，输出为S(W3S(W2S(W1x+b1)+b2)+b3)

       同时简记住每层在激活函数处理前的值为ai, 输出为fi

       假设最后损失函数为L，L是一个关于f3的函数，那么求导易得

[begin{array}{l} frac{{partial L}}{{partial {W_1}}} = frac{{partial L}}{{partial {f_3}}} cdot frac{{partial Sleft( {{W_3}Sleft( {{W_2}Sleft( {{W_1}x + {b_1}} right) + {b_2}} right) + {b_3}} right)}}{{partial {W_1}}} \ quad quad = frac{{partial L}}{{partial {f_3}}} cdot frac{{partial S}}{{partial {a_3}}} cdot frac{{partial {W_3}Sleft( {{W_2}Sleft( {{W_1}x + {b_1}} right) + {b_2}} right) + {b_3}}}{{partial {W_1}}} \ quad quad = frac{{partial L}}{{partial {f_3}}} cdot frac{{partial S}}{{partial {a_3}}} cdot {W_3} cdot frac{{partial Sleft( {{W_2}Sleft( {{W_1}x + {b_1}} right) + {b_2}} right)}}{{partial {W_1}}} \ quad quad = cdots \ quad quad = frac{{partial L}}{{partial {f_3}}} cdot frac{{partial S}}{{partial {a_3}}} cdot {W_3} cdot frac{{partial S}}{{partial {a_2}}} cdot {W_2} cdot frac{{partial S}}{{partial {a_1}}} cdot frac{{partial {a_1}}}{{partial {W_1}}} \ end{array}]

       其中偏导数∂S/ ∂ai是造成梯度消失的原因，因为S函数的导数阈值为

[f'left( x right) = frac{{{e^{ – x}}}}{{{{left( {1 + {e^{ – x}}} right)}^2}}};; in left( {0,left. {frac{1}{4}} right]} right.]

       即有0<∂S/ ∂a1≤0.25， 0<∂S/ ∂a2≤0.25， 0<∂S/ ∂3≤0.25, 在损失函数偏导表达式中三个偏导数相乘有:

[0 < frac{{partial S}}{{partial {a_3}}}frac{{partial S}}{{partial {a_2}}}frac{{partial S}}{{partial {a_1}}} le 0.015625]

       这样会减小损失函数的数值，如果神经网络是20层，则有

[0 < frac{{partial S}}{{partial {a_{20}}}}frac{{partial S}}{{partial {a_{19}}}} cdots frac{{partial S}}{{partial {a_1}}} le {0.25^{20}} = {rm{9}}.0{rm{94}} times {10^{ – 13}}]

       这是一个更小的数，所以神经网络后几层求第一层参数W1的梯度就非常小。而ReLU函数就是为了避免梯度消失问题，因为ReLU求导只有两个值1或0，这样的话只要神经网络梯度中一条路径上的导数都是1，那么无论网络有多少层，网络后几层的梯度都可以传播到网络前几层。

参考资料

1. https://en.wikipedia.org/wiki/Logistic_function
2. https://en.wikipedia.org/wiki/Hyperbolic_function
3. https://en.wikipedia.org/wiki/Rectifier_(neural_networks)