C++算法 线段树
线段树这个算法,看起来非常高端,而且很有用处,所以还是讲一下下吧。
温馨提示:写线段树前请做好写码5分钟,调试一辈子的准备^-^
啊直接步入正题……
首先我们考虑一个题目:有一个序列,要做到单点修改单点查询,该怎么做呢?
同学们先不要着急关掉……我们细细分析,像这种题,明显大家都知道……直接暴力就过了嘛……,所以不做分析……
然后我们考虑第二个题目:有一个序列,要做到单点修改区间求和,该怎么做呢?
像传统的for(int i=1;i<=n;i++)ans+=a[i]当然是很香的,但如果遇到一些非常奇怪的题目(数 据 大 到 你 自 闭),这个就没什么用了……
啊这,简单的暴力不能用,就要用复杂的暴力——线段树,当然是简单亿点点的~因为单点修改可以O(1),不存在浪费时间的事情,所以我们用线段树小小的处理一下就好了。
接下来画一个图帮助斯烤:
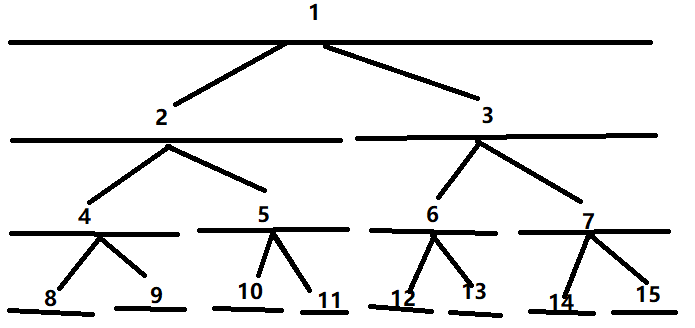
在这个图上呢……一共有8个点,就是底下那些最小的线段,而我们把他合成了许多部分,每个部分的值就是f[wz*2]+f[wz*2+1](f是每个的值,wz是每个的编号)。
然后就可以把他一直向下,一直向下,直到发现这个区间是被我们要求的区间所包含的,然后这个区间内的数就全部加上,就这么一直向下找找找……,最后就可以算出一个区间的总和。
下面是演示代码~
void qh(long long wz)//wz是现在所处的小块编号
{
if(tree[wz].l>=a&&tree[wz].r<=b)//a和b是我们要求的区间的左右端点
{
zshu+=tree[wz].shu;//全部被包含,直接加上
return;
}
long long mid=(tree[wz].l+tree[wz].r)/2;//不能被包含?分裂一下试试吧
if(b>mid)//和谐小细节~
{
qh(wz*2+1);//如果有被包含,就去右边的小块看看
}
if(a<=mid)//和谐小细节*2~(至于为啥有和谐小细节,以及为什么要这样写,请同学们自己斯烤(这么简单还是可以的8))
{
qh(wz*2);//如果有被包含,也要去左边的小块看看
}
}
嘿嘿简单吧^-^,啊我忘记讲建树了QAQ。没事马上就讲。
建树嘛,直接递归就好了,每次把这个区间分成两份,一直分到l和r一样(就是说这是一个点的值,要输入了),然后获取两个点的值之后就可以向上递归~嗯嗯对,一直递归就建好了,相信大家都有这个写递归的能力,但要实在不会就看看下面的代码吧(温馨提示:线段树用来建树的数组要开到节点数的4倍大,至于为什么我也忘了……):
struct hehe
{
long long l,r,shu,f;
}tree[400005];//tree结构体~
long long mid;
void js(long long ll,long long rr,long long wz)//js,建树的意思。ll和rr分别是左右边界,wz就是他的编号
{
tree[wz].l=ll;//左边界是ll
tree[wz].r=rr;//右边界是rr
if(ll==rr)//左右边界一致,这是一个点
{
scanf("%lld",&tree[wz].shu);
return;
}
long long mid=(ll+rr)/2;//如果这不是一个点,肯定能分成两部分
js(ll,mid,wz*2);//左边
js(mid+1,rr,wz*2+1);//右边
tree[wz].shu=tree[wz*2].shu+tree[wz*2+1].shu;//加起来
}
看,是不是非常简单,接下来为了学的更深一点点,要把题目加难了(是的还要加难,但我相信你们一定可以学会的)
有一个序列,要做到区间增加区间求和,该怎么做呢?
啊这,这个是线段树里最难的一部分(起码我觉得最难),直接下放显然不太现实……,会浪费掉很多不必要的时间。正所谓科技发展在于懒人~,其实我们也可以在不影响结果的情况下偷个懒是吧QWQ。
就像加一样~我知道这两个序列的和,我就没必要去求所有单个序列是多少,加法和这个差不多,我们可以看看有那个序列是全都要加的,然后直接算出它加完之后的值。这样求这个值的时候肯定是不影响计算的(偷懒成功!)。但这时就会有一些同学吐槽:”啊你这个不严谨啊,如果下一次求和是求这个序列的一部分怎么办呢?”其实呢,我刚才也写了是吧……
其实我们也可以在不影响结果的情况下偷个懒是吧
我刚才说的是不影响,但这个操作明显影响了,在哪里影响了呢?就是只加了一个总序列,没有让他的一部分加上(偷懒失败QWQ)。但好像根本没有必要调整他的一部分啊,因为目前根本用不到,没说让做的事情我们还要去做不是浪费时间吗?但又不能不加,怎么办呢?我们可以设定一个懒标记,表示它之前被加了多少,这样呢,每次要求和的时候只要下放这个懒标记,并且加上该加的数,就能达到不说不做,最大程度优化时间,还保证正确hhhhh(偷懒成功)
至于代码的实现也是非常的简单:
void xf(long long wz)
{
tree[wz*2].shu+=(tree[wz*2].r-tree[wz*2].l+1)*tree[wz].f;//每个长度单位都加上tree[wz].f,总值就增加了(tree[wz*2].r-tree[wz*2].l+1)*tree[wz].f
tree[wz*2].f+=tree[wz].f;//之前每一个长度单位要加tree[wz*2].f,现在发现它还要加上tree[wz].f,就把他们两个加起来就好了嘛,很容易的。
tree[wz*2+1].shu+=(tree[wz*2+1].r-tree[wz*2+1].l+1)*tree[wz].f;
tree[wz*2+1].f+=tree[wz].f;//同理
tree[wz].f=0;//这里已经加过了,要清零的,就像转账一样,你给另一个人转了钱,你钱就没了。
}
上方是下放懒标记的代码,下方是区间修改代码:
void xg(long long wz)
{
if(tree[wz].l>=a&&tree[wz].r<=b)
{
tree[wz].shu+=(tree[wz].r-tree[wz].l+1)*c;//更改值
tree[wz].f+=c;//增加懒标记
return;
}//啊后面的都说过,不打了…
tree[wz].shu+=(min(tree[wz].r,b)-max(tree[wz].l,a)+1)*c;
long long mid=(tree[wz].l+tree[wz].r)/2;
if(b>mid)
{
xg(wz*2+1);
}
if(a<=mid)
{
xg(wz*2);
}
}
至于加了懒标记以后别的代码也是要动的。
比如在原来的求和代码里多了一个xf(wz);
至于加在哪里同学们自己斯烤吧(我太仁慈了)
啊我再放一道线段树模板题,大家可以秒掉来吊打我:模板题传送们
好了我觉得我讲完了,如果有什么不好或漏掉的地方大家可以及时评论,我会更改的。

