[NOIP2019] 划分
题目

题解
首先YY一个最简单的dp
$dp[i][j]=min(dp[j][k]+(sum[i]-sum[j])^2 (sum[i]-sum[j]>=sum[j]-sum[k])$
$dp[i][j]$表示i为终点,j为上一段起点的最小代价。
上述过程其实就是在i的左端寻找满足条件的点,然后一一计算代价并取最小值(注意这些点可能不是连续的)

但其实,我们只要取最右边的满足条件的点来更新就行了,证明见下
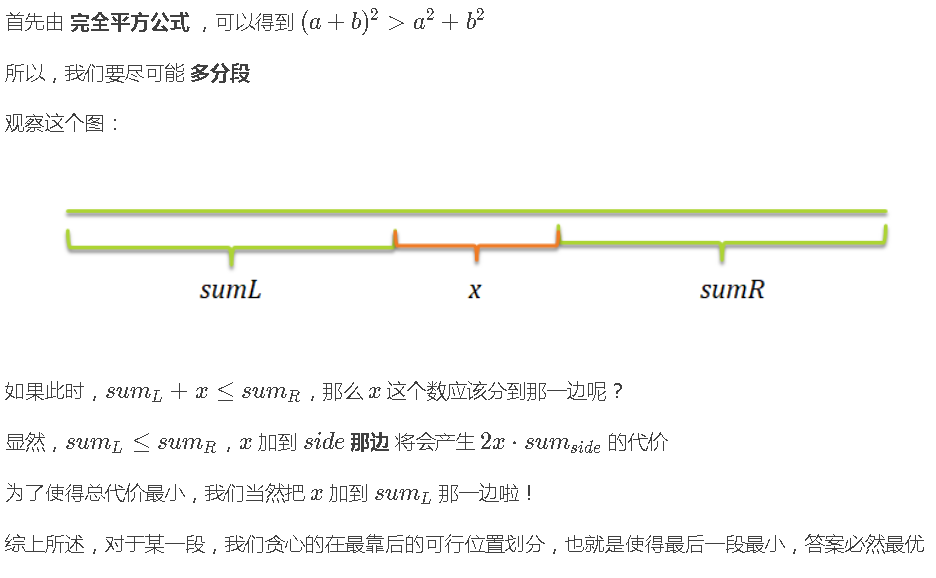
我们可以记一个$pre[i]$表示i点上一个区间的终点
这样我们就有了一个$O(n^2)$ dp
对于每个点i,我们从i往前扫,找到第一个满足 $(sum[i]-sum[j]>=sum[j]-sum[pre[j])$ 的点j ,则
$dp[i]=dp[j]+(sum[i]-sum[j])^2$
注意到如果一个点j满足i,那么它肯定满足i+1,
如果不满足i,也可能满足i+1
另外,对于 $sum[i]-sum[j]>=sum[j]-sum[pre[j]$
可以变形成 $sum[i]>=2*sum[j]-sum[pre[j]$
那么可以设一个$d(j)=2*sum[j]-sum[pre[j]$
我们可以用一个单调队列来维护满足条件的点
因为我们只需要最右边满足条件的点,所以每次i递增的时候,如果队头下一位也满足条件,就把队头踢掉(因为下一位肯定比队头更右)
然后用队头更新这一位的dp值
然后把这一位从队尾插入,并把前面d值大于它的点全部删除
这样就可以做到$O(n)$了
代码
这个是88分的,100分的要写高精,但正确性是有的。
#include <iostream>
#include <cstdio>
#define int long long
using namespace std;
#define N 4*(int)1e7+10
int sum[N],pre[N],q[N],dp[N],l=1,r=0;
#define val(a) (2*sum[a]-sum[pre[a]])
signed main()
{
int n,type;
cin>>n>>type;
for(int i=1;i<=n;i++)
{
int a;
scanf("%lld",&a);
sum[i]=sum[i-1]+a;
}
q[++r]=0;
for(int i=1;i<=n;i++)
{
while(l<r&&val(q[l+1])<=sum[i]) l++;
pre[i]=q[l];
dp[i]=dp[pre[i]]+(sum[i]-sum[pre[i]])*(sum[i]-sum[pre[i]]);
while(l<=r&&val(i)<=val(q[r])) r--;
q[++r]=i;
}
cout<<dp[n];
}

