python常用算法学习（4）——数据结构

2019 年 10 月 18 日
筆記

数据结构简介

1，数据结构

　　数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成。简单来说，数据结构就是设计数据以何种方式组织并存贮在计算机中。比如：列表，集合与字典等都是一种数据结构。而之前已经学习过列表，字典，集合，元组等，这里就简单说一下不再赘述。

　　N.Wirth：“程序=数据结构+算法”

　　数据：数据即信息的载体，是能够输入到计算机中并且能被计算机识别，存储和处理的符号总称。

　　数据元素：数据元素是数据的基本单位，又称之为记录（Record），一般，数据元素若由若干基本型（或称字段，域，属性）组成。

2，数据结构的分类

　　数据结构按照其逻辑结构可分为线性结构，树结构，图结构

线性结构：数据结构中的元素存在一对一的相互关系
树结构：数据结构中的元素存在一对多的相互关系
图结构：数据结构中的元素存在多对多的相互关系

3，存储结构

1，特点

1，是数据的逻辑结构在计算机存储器中的映象（或表示）
2，存储结构是通过计算机程序来实现，因而是依赖于具体的计算机语言的

2，存储结构分类

1，顺序存储（Sequential Storage）：将数据结构中各元素按照其逻辑顺序存放于存储器一片连续的存储空间中。
2，链式存储（Linkend Storage）：将数据结构中各元素分布到存储器的不通电，用记录下一个结点位置的方式建立他们之间的联系，由此得到的存储结构为链式存储结果。
3，索引存储（Indexed Storage）：在存储数据的同时，建立一个附加的索引表，即索引存储结构=数据文件+索引表。

常用的数据结构

1，列表

　　列表（其他语言称为数组，但是数组和Python的列表还是有区别的）是一种基本数据类型。

　　列表，在Python中称为list，使用中括号包含，其中内部元素使用逗号分隔，内部元素可以是任何类型包含空。

1.1 数组和列表不同点

1，数组元素类型要相同，而Python列表不需要
2，数组长度固定，而Python列表可以增加

　　Python列表操作方法请参考此博客：https://www.cnblogs.com/wj-1314/p/8433116.html

2，元组

　　元组，Python中类为tuple。使用小括号包含，内部元素使用逗号分隔，可为任意值。与列表不同之处为，其内部元素不可修改，而且不能做删除，更新操作。

　　注意：当元组中元素只有一个时，结尾要加逗号，若不加逗号，Python解释器都将解释成元素本身的类型，而非元组类型。

　　举个例子：

>>> a = (1,2,3)  >>> b = ('1',[2,3])  >>> c = ('1','2',(3,4))  >>> d = ()  >>> e = (1,)

2.1 元组的操作

　　通过下标操作

通过小标来获取元素值，使用方法同列表
切片的处理，使用方法同列表
不可通过下标做删除和更新操作

　　如下，做出更改和删除会报异常：

>>> c[0] = 1  Traceback (most recent call last):    File "<stdin>", line 1, in <module>  TypeError: 'tuple' object does not support item assignment    >>> del c[0]  Traceback (most recent call last):    File "<stdin>", line 1, in <module>  TypeError: 'tuple' object doesn't support item deletion

2.2 运算符及内建函数操作

　　元组本身是不可变，但是可以通过 + 来构成新的元组。

>>> a  (1, 2, 3)  >>> b  ('1', [2, 3])  >>> a + b  (1, 2, 3, '1', [2, 3])

　　可以通过使用内建函数 len 获取元组长度，可以使用 * 元素来实现元素的重复

>>> a = (1,2,3)  >>> len(a)  3  >>> a*3  (1, 2, 3, 1, 2, 3, 1, 2, 3)

　　元组也支持 in 和 not in 成员运算符。

3，集合

　　集合用于包含一组无序的对象，与列表和元组不同，集合是无序的，也无法通过数字进行索引。此外，集合中的元素不能重复。set和dict一样，只是没有 value，相当于 dict 的 key 集合，由于 dict 的 key 是不重复的，且 key 是不可变对象，因此 set 有如下特性：

1，不重复，（互异性），也就是说集合是天生去重的
2，元素为不可变对象，（确定性，元素必须可 hash）
3，集合的元素没有先后之分，（无序性）

　　Python的集合与数学中的集合一样，也有交集，并集和合集。

　　举例如下：

>>> s1 = {1,2,3,4,5}  >>> s2 = {1,2,3}  >>> s3 = {4,5}  >>> s1&s2   # 交集  {1, 2, 3}  >>> s1|s2   # 并集  {1, 2, 3, 4, 5}  >>> s1 - s2  # 差差集  {4, 5}  >>> s3.issubset(s1)   # s3 是否为s1 的子集  True  >>> s1.issuperset(s2)  # s1 是否为 s2 的超集  True

　　更多集合相关的操作参考博客：https://www.cnblogs.com/wj-1314/p/8423273.html

4，栈

　　栈（Stack）是一个数据集合，可以理解为只能在一段进行插入或删除操作的列表。

　　栈的特点：后进先出 LIFO（Last-in， First-out）

　　栈的概念有：栈顶，栈底

　　栈的基本操作：

进栈（压栈）：push
出栈：pop
取栈顶：gettop

　　对栈的理解，就像是一摞书，只能从上面放和取。

4.1 栈的实现

　　使用一般列表结构即可实现栈：

进栈：li.append
出栈：li.pop
取栈顶：li[-1]

　　那现在我们写一个类实现它：

class Stack:        def __init__(self):          self.stack = []        def push(self, element):          self.stack.append(element)        def pop(self):          # 移除列表中的一个元素（默认最后一个），并返回该元素的值          return self.stack.pop()        def get_top(self):          if len(self.stack) > 0:              return self.stack[-1]          else:              return None    stack = Stack()  stack.push(1)  stack.push(2)  print(stack.pop())   # 2

4.2 栈的应用——括号匹配问题

　　我们可以通过栈来解决括号匹配的问题，就是解决IDE实现括号未匹配成功报错的问题。

　　代码：

class Stack:        def __init__(self):          self.stack = []        def push(self,element):          return self.stack.append(element)        def pop(self):          return self.stack.pop()        def get_top(self):          if len(self.stack) > 0:              return self.stack[-1]          else:              return None        def is_empty(self):          return len(self.stack) == 0    def brace_match(s):      match = {'}': '{', ']': '[', ')': '('}      stack = Stack()      for ch in s:          if ch in {'(', '[', '{'}:              stack.push(ch)          else:              if stack.is_empty():                  return False              elif stack.get_top() == match[ch]:                  stack.pop()              else:                  return False        if stack.is_empty():          return True      else:          return False    print(brace_match('{[{()}]}'))

5，队列

　　队列（Queue）是一个数据集合，仅允许在列表的一端进行插入，另一端进行删除。进行插入的一端称为队尾（rear），插入动作称为进队或者入队。进行删除的一端称为对头（front），删除动作称为出队。

　　队列的性质：先进先出（First-in , First-out）

　　队列可以并发的派多个线程，对排列的线程处理，并切每个需要处理线程只需要将请求的数据放入队列容器的内存中，线程不需要等待，当排列完毕处理完数据后，线程在准时来取数据即可，请求数据的线程只与这个队列容器存在关系，处理数据的线程down掉不会影响到请求数据的线程，队列会派给其他线程处理这份数据，它实现了解耦，提高效率。队列内会有一个顺序的容器，列表与这个容器是有区别的，列表中数据虽然是排列的，但数据被取走后还会保留，而队列中这些容器的数据被取后将不会保留。当必须在多个线程之间安全的交换信息时，队列在线程编程中特别有用。

5.1 队列的实现

　　队列能否用列表简单实现？为什么？

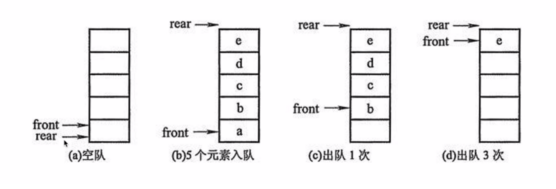
环形队列的实现方式

　　环形队列：当队尾指针 front == MaxSize + 1 时，再前进一个位置就自动到0。

队首指针前进1： front = (front + 1) % MaxSize
队尾指针前进1： rear = (rear + 1) % MaxSize
队空条件： front == rear
队满条件： (rear + 1) % MaxSize == front

class Queue:        def __init__(self, size):          self.queue = [0 for _ in range(size)]          self.size = size          self.rear = 0  # 队尾指针是进队的          self.front = 0  # 对首指针是出队的        def push(self, element):          if not self.is_filled():              rear = (self.rear + 1) % self.size              self.queue[self.rear] = element          else:              raise IndexError("Queue is filled")        def pop(self):          if not self.is_empty():              self.front = (self.front + 1) % self.size              return self.queue[self.front]          else:              raise IndexError("Queue is empty")        # 判断队空      def is_empty(self):          return self.rear == self.front        # 判断队满      def is_filled(self):          return (self.rear + 1) % self.size == self.front    q = Queue(5)  for i in range(4):      q.push(i)    print(q.pop())

from collections import deque    q = deque()  q.append(1)  # 队尾进队  print(q.popleft())  # 对首出队    # 用于双向队列  q.appendleft(1)  # 队首进队  print(q.pop())   #队尾出队

　　双向队列的完整用法：

# _*_coding:utf-8_*_    # 创建双向队列  from collections import deque    d = deque()    # append（往右边添加一个元素）  d.append(1)  d.append(2)  print(d)  # deque([1, 2])    # appendleft（往左边添加一个元素）  d.appendleft(11)  d.appendleft(22)  print(d)  # deque([22, 11, 1, 2])    # clear清空队列  d.clear()  print(d)  # deque([])    # 浅copy copy  d.append(1)  new_d = d.copy()  print(new_d)  # deque([1])    #  count(返回指定元素的出现次数)  d.append(1)  d.append(1)  print(d)  # deque([1, 1, 1])  print(d.count(1))  # 3    # extend(从队列右边扩展一个列表的元素)  d.append(2)  d.extend([3, 4, 5])  print(d)  # deque([1, 1, 1, 2, 3, 4, 5])    # extendleft(从队列左边扩展一个列表的元素)  d.extendleft([3, 4, 5])  print(d)  # deque([5, 4, 3, 1, 1, 1, 2, 3, 4, 5])    #  index（查找某个元素的索引位置）  d.clear()  d.extend(['a', 'b', 'c', 'd', 'e'])  print(d)  print(d.index('e'))  print(d.index('c', 0, 3))  # 指定查找区间  '''  deque(['a', 'b', 'c', 'd', 'e'])  4  2  '''    #  insert（在指定位置插入元素）  d.insert(2, 'z')  print(d)  # deque(['a', 'b', 'z', 'c', 'd', 'e'])    # pop（获取最右边一个元素，并在队列中删除）  x = d.pop()  print(x)  print(d)  '''  e  deque(['a', 'b', 'z', 'c', 'd'])  '''    # popleft（获取最左边一个元素，并在队列中删除）  print(d)  x = d.popleft()  print(x)  print(d)  '''  deque(['a', 'b', 'z', 'c', 'd'])  a  deque(['b', 'z', 'c', 'd'])  '''    # remove（删除指定元素）  print(d)  d.remove('c')  print(d)  '''  deque(['b', 'z', 'c', 'd'])  deque(['b', 'z', 'd'])  '''    # reverse（队列反转）  print(d)  d.reverse()  print(d)  '''  deque(['b', 'z', 'd'])  deque(['d', 'z', 'b'])  '''    # rotate（把右边元素放到左边）  d.extend(['a', 'b', 'c', 'd', 'e'])  print(d)  d.rotate(2)  # 指定次数，默认1次  print(d)  '''  deque(['d', 'z', 'b', 'a', 'b', 'c', 'd', 'e'])  deque(['d', 'e', 'd', 'z', 'b', 'a', 'b', 'c'])  '''

Python四种类型的队列

　　Queue：FIFO 即 first in first out 先进先出

　　LifoQueue：LIFO 即 last in first out 后进先出

　　PriorityQueue：优先队列，级别越低，越优先

　　deque：双边队列

导入三种队列，包

from queue import Queue,LifoQueue,PriorityQueue

Queue：先进先出队列

#基本FIFO队列  先进先出 FIFO即First in First Out,先进先出  #maxsize设置队列中，数据上限，小于或等于0则不限制，容器中大于这个数则阻塞，直到队列中的数据被消掉  q = Queue(maxsize=0)    #写入队列数据  q.put(0)  q.put(1)  q.put(2)    #输出当前队列所有数据  print(q.queue)  #删除队列数据，并返回该数据  q.get()  #输也所有队列数据  print(q.queue)    # 输出:  # deque([0, 1, 2])  # deque([1, 2])

LifoQueue：后进先出队列：

#LIFO即Last in First Out,后进先出。与栈的类似，使用也很简单,maxsize用法同上  lq = LifoQueue(maxsize=0)    #队列写入数据  lq.put(0)  lq.put(1)  lq.put(2)    #输出队列所有数据  print(lq.queue)  #删除队尾数据，并返回该数据  lq.get()  #输出队列所有数据  print(lq.queue)    #输出:  # [0, 1, 2]  # [0, 1]

优先队列

# 存储数据时可设置优先级的队列  # 优先级设置数越小等级越高  pq = PriorityQueue(maxsize=0)    #写入队列，设置优先级  pq.put((9,'a'))  pq.put((7,'c'))  pq.put((1,'d'))    #输出队例全部数据  print(pq.queue)    #取队例数据，可以看到，是按优先级取的。  pq.get()  pq.get()  print(pq.queue)    #输出：  [(9, 'a')]

双边队列

#双边队列  dq = deque(['a','b'])    #增加数据到队尾  dq.append('c')  #增加数据到队左  dq.appendleft('d')    #输出队列所有数据  print(dq)  #移除队尾，并返回  print(dq.pop())  #移除队左，并返回  print(dq.popleft())  #输出:  deque(['d', 'a', 'b', 'c'])  c  d

6，链表

　　当我们存储一大波数据时，我们很多时候是使用数组，但是当我们执行插入操作的时候就是非常麻烦，比如，有一堆数据1,2,3,5,6,7 我们要在3和5之间插入4，如果用数组，我们会怎么办？当然是将5之后的数据往后退一位，然后再插入4，这样非常麻烦，但是如果用链表，就直接在3和5之间插入4即可。

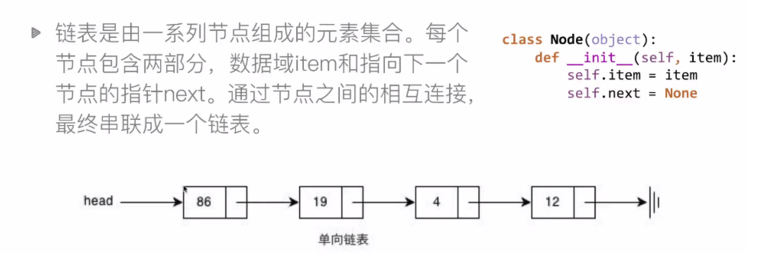
　　所以链表的节点结构如下：

　　data为自定义的数据，next为下一个节点的地址。head保存首位节点的地址。

　　首先可以看一个小链表，定义链表：

class Node:      def __init__(self, item):          self.item = item          self.next = None    a = Node(1)  b = Node(2)  c = Node(3)  # 通过next 将 a,b,c联系起来  a.next = b  b.next = c  # 打印a的下一个的下一个结果是什么  print(a.next.next.item) # 3

　　当然，我们不可能这样next来调用链表，使用循环等，下面继续学习。

　　链表永远有一个头结点，head

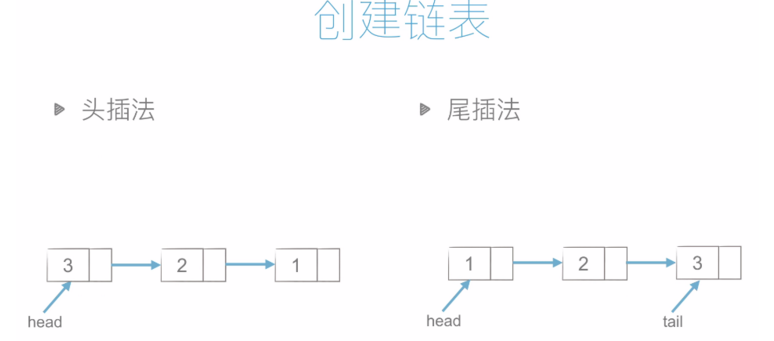
　　头插法和尾插法的代码如下：

class Node:      def __init__(self, item):          self.item = item          self.next = None    # 头插法  # 这里我们使用 li 进行循环插入  def create_linklist_head(li):      head = Node(li[0])      for element in li[1:]:          node = Node(element)          node.next = head  # 将头结点 给刚插入的节点          head = node       # 然后将插入的节点设置为头结点      return head    # 尾插法  def create_linklist_tail(li):      head = Node(li[0])      tail = head      for element in li[1:]:          node = Node(element)          tail.next = node          tail = node      return head    def print_linklist(lk):      while lk:          print(lk.item, end=',')          lk = lk.next      print('*********')    lk = create_linklist_head([1, 2, 3, 4])  # print(lk.item)  # 4  print_linklist(lk)  # 4,3,2,1,*********    lk = create_linklist_tail([1, 2, 3, 4, 5])  print_linklist(lk)  # 1,2,3,4,5,

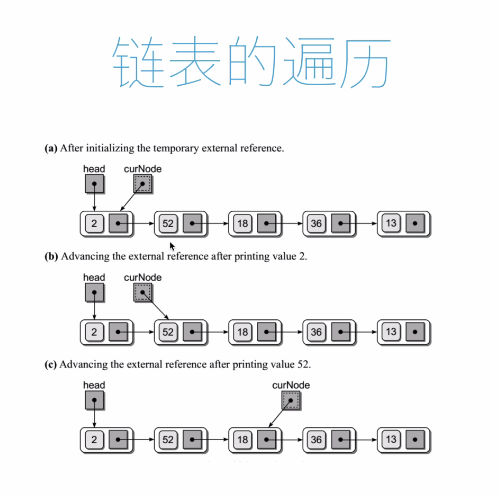
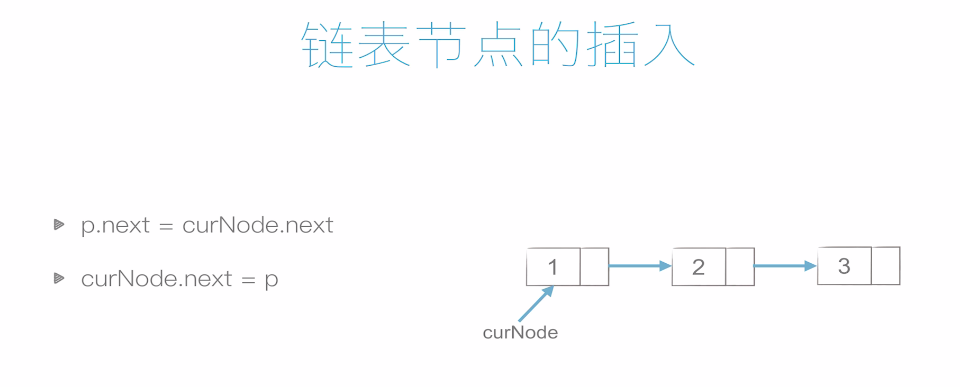
　　插入如下，非常简单，所以时间复杂度也低。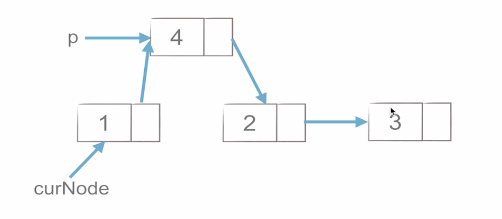

6.1 关于链表的方法

　　1，判断是否为空：isEmpty()

def isEmpty(self):      return (self.length == 0)

　　2，增加一个节点（在链表尾添加）：append()

def append(self, dataOrNode):      item = None      if isinstance(dataOrNode, Node):          item = dataOrNode      else:          item = Node(dataOrNode)        if not self.head:          self.head = item          self.length += 1      else:          node = self.head          while node._next:              node = node._next          node._next = item          self.length += 1

　　3，删除一个节点：delete()

# 删除一个节点之后，记得把链表长度减一  def delete(self, index):      if self.isEmpty():          print("this chain table is empty")          return        if index < 0 or index >= self.length:          print('Error: out of index')          return        # 要注意删除第一个节点的情况，如果有空的头节点就不用这样      if index == 0:          self.head = self.head._next          self.length -= 1          return        # prev 为保存前导节点      # node 为保存当前节点      # 当j 与index 相等时就相当于找到要删除的节点      j = 0      node = self.head      prev = self.head      while node._next and j < index:          prev = node          node = node._next          j += 1        if j == index:          prev._next = node._next          self.length -= 1

　　4，修改一个节点：update()

def update(self, index, data):      if self.isEmpty() or index < 0 or index >= self.length:          print 'error: out of index'          return      j = 0      node = self.head      while node._next and j < index:          node = node._next          j += 1        if j == index:          node.data = data

　　5，查找一个节点：getItem()

def getItem(self, index):      if self.isEmpty() or index < 0 or index >= self.length:          print "error: out of index"          return      j = 0      node = self.head      while node._next and j < index:          node = node._next          j += 1        return node.data

　　6，查找一个节点的索引：getIndex()

def getIndex(self, data):      j = 0      if self.isEmpty():          print "this chain table is empty"          return      node = self.head      while node:          if node.data == data:              return j          node = node._next          j += 1        if j == self.length:          print "%s not found" % str(data)          return

　　7，插入一个节点：insert()

def insert(self, index, dataOrNode):      if self.isEmpty():          print "this chain tabale is empty"          return        if index < 0 or index >= self.length:          print "error: out of index"          return        item = None      if isinstance(dataOrNode, Node):          item = dataOrNode      else:          item = Node(dataOrNode)        if index == 0:          item._next = self.head          self.head = item          self.length += 1          return        j = 0      node = self.head      prev = self.head      while node._next and j < index:          prev = node          node = node._next          j += 1        if j == index:          item._next = node          prev._next = item          self.length += 1

　　8，清空链表：clear()

def clear(self):      self.head = None      self.length = 0

6.2 双链表

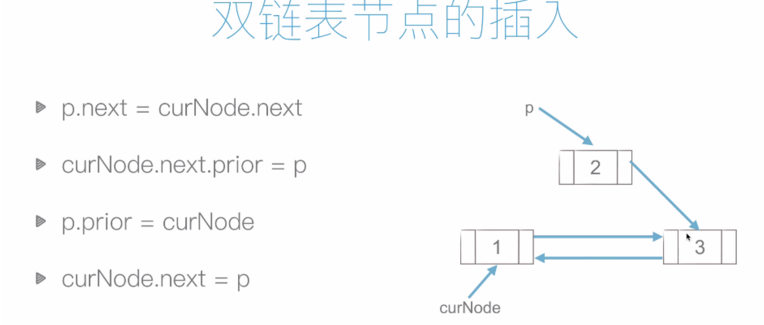
6.3 链表复杂度分析

　　顺序表（列表/数组）与链表

按照元素值查找
按下标查找
在某元素后插入
删除某元素

　链表与顺序表

链表在插入和删除的操作上明显快于顺序表
链表的内存可以更加灵活地分配（可以试利用链表重新实现栈和队列）
链表这种链式存储的数据结构对树和图的结构有很大的启发性

7，哈希表（Hash table）

　　众所周知，HashMap是一个用于存储 Key-Value键值对的集合，每一个键值对也叫Entry，这些键值对（Entry）分散存储在一个数组当中，这个数组就是HashMap的主干。

　　使用哈希表可以进行非常快速的查找操作，查找时间为常数，同时不需要元素排列有序；Python的内建数据类型：字典就是用哈希表实现的。

　　Python中的这些东西都是哈希原理：字典(dictionary)、集合(set)、计数器(counter)、默认字典Defaut dict)、有序字典(Order dict).

　　哈希表示一个高效的查找的数据结构，哈希表一个通过哈希函数来计算数据存储位置的数据结构，通常支持如下操作：

insert(key, value)：插入键值对（key, value）
get(key)：如果存在键为key的键值对则返回其value，否则返回空值
delete(key)：删除键为key的键值对

直接寻址表

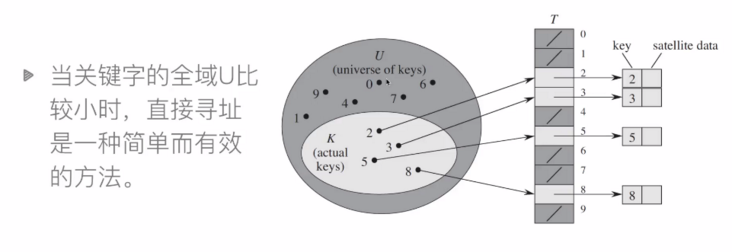
直接寻址技术缺点：

当域U很大时，需要消耗大量内存，很不实际
如果域U很大而实际出现的key很少，则大量空间被浪费
无法处理关键字不是数字的情况

哈希

　　直接寻址表：key为k的元素放到k位置上

　　改进直接寻址表：哈希（Hashing）

构建大小为m的寻址表T
key为k的元素放到 h(k)位置上
h(k) 是一个函数，其将域U映射到表 T[0, 1, … , m-1]

哈希表

　　哈希表（Hash Table，又称为散列表），是一种线性表的存储结构。哈希表由一个直接寻址表和一个哈希函数组成。哈希函数h(k)将元素关键字 k 作为自变量，返回元素的存储下标。

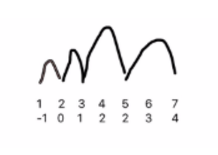
　　假设有一个长度为7的哈希表，哈希函数 h(k)=k%7.元素集合 {14, 22, 3, 5}的存储方式如下图：

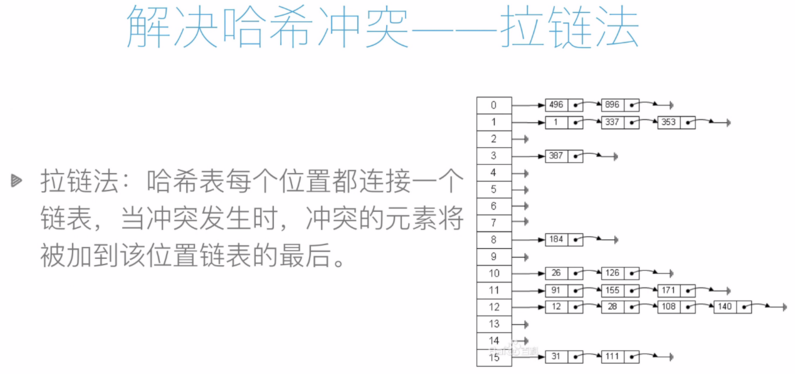
　　代码如下：

class LinkList:      class Node:          def __init__(self, item=None):              self.item = item              self.next = None        class LinkListIterator:          def __init__(self, node):              self.node = node          def __next__(self):              if self.node:                  cur_node = self.node                  self.node = cur_node.next                  return cur_node.item              else:                  raise StopIteration          def __iter__(self):              return self        def __init__(self, iterable=None):          self.head = None          self.tail = None          if iterable:              self.extend(iterable)        def append(self, obj):          s = LinkList.Node(obj)          if not self.head:              self.head = s              self.tail = s          else:              self.tail.next = s              self.tail = s        def extend(self, iterable):          for obj in iterable:              self.append(obj)        def find(self, obj):          for n in self:              if n == obj:                  return True          else:              return False        def __iter__(self):          return self.LinkListIterator(self.head)        def __repr__(self):          return "<<" + ",".join(map(str, self)) + ">>"      # 类似于集合的结构  class HashTable:      def __init__(self, size=101):          self.size = size          self.T = [LinkList() for i in range(self.size)]        def h(self, k):          return k % self.size        def insert(self, k):          i = self.h(k)          if self.find(k):              print('Duplicated Insert')          else:              self.T[i].append(k)        def find(self, k):          i = self.h(k)          return self.T[i].find(k)

7.1 哈希表的应用

　　1，集合与字典

　　字典与集合都是通过哈希表来实现的。比如：

dic_res = {'name':'james', 'age':32, 'gender': 'Man'}

　　使用哈希表存储字典，通过哈希表将字典的键映射为下标，假设 h(‘name’)=3，h(‘age’)=4，则哈希表存储为：

[None, 32, None, 'james', 'Man']

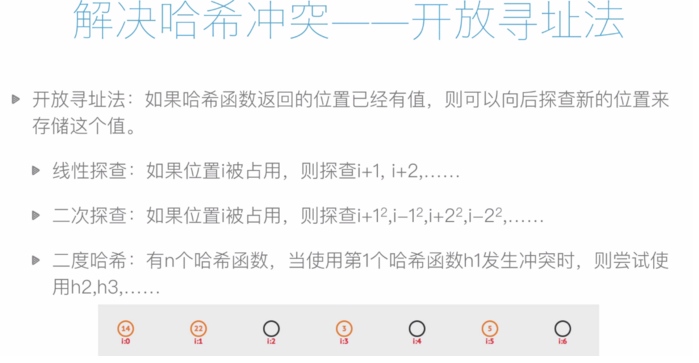
　　如果发生哈希冲突，则通过拉链法或开发寻址法解决。

　　2，md5算法

　　MD5（Message-Digest Algorithm 5）曾经是密码学中常用的哈希函数，可以把任意长度的数据映射为128位的哈希值，其曾经包含如下特征：

1，同样的消息，其MD5值必定相同；
2，可以快速计算出任意给定消息的MD5值；
3，除非暴力的枚举所有可能的消息，否则不可能从哈希值反推出消息本身；
4，两天消息之间即使只有微小的差别，其对应的MD5值也应该是完全不同，完全不相关的；
5，不能再有意义的时间内人工的构造两个不同的消息，使其具有相同的MD5值

　　3，md5

　　应用举例：文件的哈希值

　　算出文件的哈希值，若两个文件的哈希值相同，则可认为这两个文件时相同的，因此：

1，用户可以利用它来验证下载的文件是否完整
2，云存储服务商可以利用它来判断用户要上次的文件是否已经存在于服务器上，从而实现秒传的功能，同时避免存储过多相同的文件副本。

　　 4，SHA2算法

　　历史上MD5和SHA-1曾经是使用最为广泛的 cryptographic hash function，但是随着密码学的发展，这两个哈希函数的安全性相继受到了各种挑战。

　　因此现在安全性较重要的场合推荐使用 SHA-A等新的更安全的哈希函数。

　　SHA-2包含了一系列的哈希函数：SHA-224， SHA-256， SHA-384，SHA-512，SHA-512/224，SHA-512/256，其对应的哈希值长度分别为 224， 256， 384 or 512位。

　　SHA-2 具有和 MD5 类似的性质。

　　5，SHA2算法应用举例

　　例如在比特币系统中，所有参与者需要共同解决如下问题：对于一个给定的字符串U，给定的目标哈希值H，需要计算一个字符串V，使得 U+ V的哈希值与H的差小于一个给定值D。此时，只能通过暴力枚举V来进行猜测。首先计算出结果的人可获得一定奖金。而某人首先计算成功的概率与其拥有的计算量成正比，所以其获得的奖金的期望值与其拥有的计算量成正比。

栈和队列的应用——迷宫问题

　　给出一个二维列表，表示迷宫（0表示通道，1表示围墙）。给出算法，求一条走出迷宫的路径。

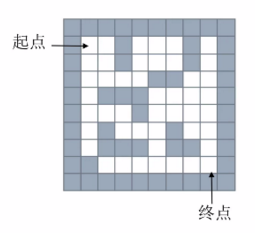
　　将其转化为数组如下：

　　那有两种思路，一种是使用栈（深度优先搜索）来存储当前路径，也可以称为回溯法。但是深度优先有一个缺点，就是虽然能找到路径，但是不能保证是最短路径，其优点就是简单，容易理解。

另一种方法就是队列，

1，栈——深度优先搜索

　　回溯法

　　思路：从一个节点开始，任意找下一个能走的点，当炸不到能走的点时，退回上一个点寻找是否有其他方向的点。

　　使用栈存储当前路径

　　如下图所示：

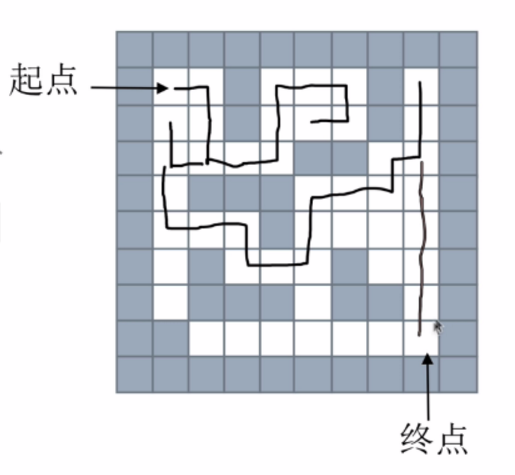
　　代码如下：

# _*_coding:utf-8_*_    maze = [      [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],      [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],      [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],      [1, 0, 0, 0, 0, 1, 1, 0, 0, 1],      [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],      [1, 0, 0, 0, 1, 0, 0, 0, 0, 1],      [1, 0, 1, 0, 0, 0, 1, 0, 0, 1],      [1, 0, 1, 1, 1, 0, 1, 1, 0, 1],      [1, 1, 0, 0, 0, 0, 0, 0, 0, 1],      [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]  ]    # 这里我们封装一个列表,用来表示走迷宫的四个方向  dirs = [      lambda x, y: (x + 1, y),  # 表示向上走      lambda x, y: (x - 1, y),  # 表示向下走      lambda x, y: (x, y - 1),  # 表示向左走      lambda x, y: (x, y + 1),  # 表示向右走  ]      def maze_path(x1, y1, x2, y2):      stack = []      stack.append((x1, y1))      while (len(stack) > 0):          curNode = stack[-1]  # 当前节点是 stack最后一个位置          if curNode[0] == x2 and curNode[1] == y2:              return True  # 如果有路则返回TRUE，没有路则返回FALSE          # x,y当前坐标，四个方向上下左右分别是：x-1,y  x+1,y  x, y-1  x,y+1          for dir in dirs:              nextNode = dir(curNode[0], curNode[1])              # 如果下一个节点能走              if maze[nextNode[0]][nextNode[1]] == 0:                  stack.append(nextNode)                  maze[nextNode[0]][nextNode[1]] = 2  # 2表示已经走过了                  break          else:  # 如果一个都找不到，就需要回退了              maze[nextNode[0]][nextNode[1]] = 2              stack.pop()  # 栈顶出栈，也就是回退        else:          print("没有路")          return False      maze_path(1, 1, 8, 8)

2，队列——广度优先搜索

　　思路：从下一个节点开始，寻找所有接下来能继续走的点，继续不断寻找，直到找到出口。

　　使用队列存储当前正在考虑的节点

　　思路图如下：

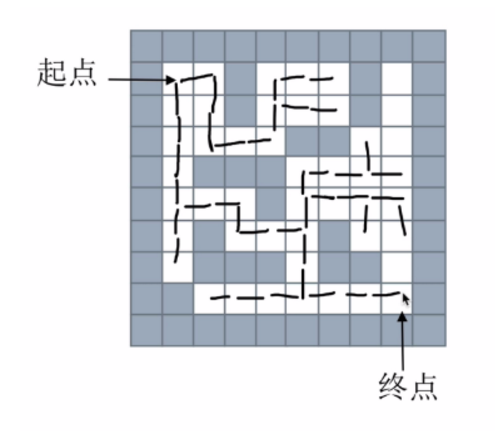
或者这样：

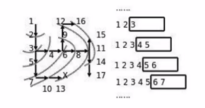
可以通过如下方式理解：

　　代码如下：

# _*_coding:utf-8_*_  from collections import deque    maze = [      [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],      [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],      [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],      [1, 0, 0, 0, 0, 1, 1, 0, 0, 1],      [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],      [1, 0, 0, 0, 1, 0, 0, 0, 0, 1],      [1, 0, 1, 0, 0, 0, 1, 0, 0, 1],      [1, 0, 1, 1, 1, 0, 1, 1, 0, 1],      [1, 1, 0, 0, 0, 0, 0, 0, 0, 1],      [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]  ]    dirs = [      lambda x, y: (x + 1, y),  # 表示向上走      lambda x, y: (x - 1, y),  # 表示向下走      lambda x, y: (x, y - 1),  # 表示向左走      lambda x, y: (x, y + 1),  # 表示向右走  ]    def print_r(path):      real_path = []  # 用来存储真实的路径      i = len(path) - 1  # 用i指向path的最后一个下标      while i >= 0:          real_path.append(path[i][0:2])          i = path[i][2]      real_path.reverse()    # 起点坐标（x1, y1)  终点坐标（x2, y2）  def maze_path_queue(x1, y1, x2, y2):      queue = deque()      path = []      # -1  为当前path的路径的下标      queue.append((x1, y1, -1))      while len(queue) > 0:  # 当队列不空时循环          # append是从右边加入的，popleft()从左边出去          cur_Node = queue.popleft()          path.append(cur_Node)          if cur_Node[0] == x2 and cur_Node[1] == y2:              # 如果当前节点等于终点节点，则说明到达终点              print_r(path)              return True            # 队列是找四个方向，每个能走就继续          for dir in dirs:              # 下一个方向的节点坐标              next_node = dir(cur_Node[0], cur_Node[1])              if maze[next_node[0]][next_node[1]] == 0:                  queue.append((next_node[0], next_node[1], len(path) - 1))                  maze[next_node[0]][next_node[1]] = 2  # 标记为已走过      return False  # 如果队列结束了，空了，还没找到路径，则为FALSE      maze_path_queue(1, 1, 8, 8)