「面试预警」二叉搜索树-双指针-贪心 算法题汇总
- 2019 年 10 月 16 日
- 筆記
本文将覆盖 「字符串处理」 + 「动态规划」 方面的面试算法题,文中我将给出:
- 面试中的题目
- 解题的思路
- 特定问题的技巧和注意事项
- 考察的知识点及其概念
- 详细的代码和解析
开始之前,我们先看下会有哪些重点案例:
为了方便大家跟进学习,我在 GitHub 建立了一个仓库
仓库地址:超级干货!精心归纳视频、归类、总结,各位路过的老铁支持一下!给个 Star !
现在就让我们开始吧!
二叉搜索树
二叉搜索树(Binary Search Tree),它或者是一棵空树,或者是具有下列性质的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树。
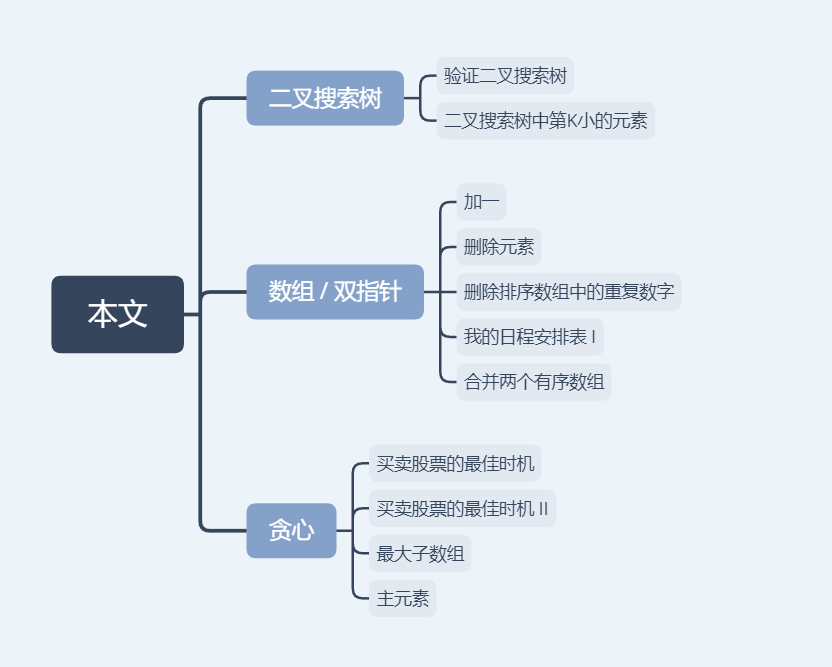
验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 :
输入: 5 / 1 4 / 3 6 输出: false 解释: 输入为: [5,1,4,null,null,3,6]。 根节点的值为 5 ,但是其右子节点值为 4 。解题思路
乍一看,这是一道很简单的题。只需要遍历整棵树,检查 node.right.val > node.val 和
node.left.val < node.val 对每个结点是否成立。
问题是,这种方法并不总是正确。不仅右子结点要大于该节点,整个右子树的元素都应该大于该节点。例如:这意味着我们需要在遍历树的同时保留结点的上界与下界,在比较时不仅比较子结点的值,也要与上下界比较。
上述思路可以用递归法实现:
- 首先将结点的值与上界和下界(如果有)比较。然后,对左子树和右子树递归进行该过程。
视频
public boolean isValidBST(TreeNode root) { return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE); } private boolean isValidBST(TreeNode root, long min, long max){ if (root == null) { return true; } if (root.val <= min || root.val >= max){ return false; } return isValidBST(root.left, min, root.val) && isValidBST(root.right, root.val, max); }二叉搜索树中第K小的元素
给定一个二叉搜索树,编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。
说明:
你可以假设 k 总是有效的,1 ≤ k ≤ 二叉搜索树元素个数。
示例 :
输入: root = [5,3,6,2,4,null,null,1], k = 3 5 / 3 6 / 2 4 / 1 输出: 3解题思路
- 增加 getCount 方法来获取传入节点的子节点数(包括自己)
- 从 root 节点开始判断k值和子节点数的大小决定递归路径是往左还是往右。
public int kthSmallest(TreeNode root, int k) { if (root == null) { return 0; } int leftCount = getCount(root.left); if (leftCount >= k) { return kthSmallest(root.left, k); } else if (leftCount + 1 == k) { return root.val; } else { //注(1) return kthSmallest(root.right, k - leftCount - 1); } } private int getCount(TreeNode root) { if (root == null) { return 0; } return getCount(root.left) + getCount(root.right) + 1; }注:
(1)为什么是 k – leftCount – 1 而不是 k ,我们可以把当前的二叉树看成左右两部分。在执行到这个条件的时候,很明显,左边 leftCount 个数,加上根节点,都小于所要求的元素。接着,现在要从右子树搜索,很明显,搜索是往下的,不可能往上(原根节点的方向)搜索,故,之前 leftCount + 1 个数作废,所以所传入 k – leftCount – 1
数组 / 双指针
所谓双指针
指的是在遍历对象的过程中,不是普通的使用单个指针进行访问,而是使用两个相同方向或者相反方向的指针进行扫描,从而达到相应的目的。
换言之,双指针法充分使用了数组有序这一特征,从而在某些情况下能够简化一些运算。
加一
给定一个非负数,表示一个数字数组,在该数的基础上+1,返回一个新的数组。该数字按照数位高低进行排列,最高位的数在列表的最前面。
示例 :
输入: [4,3,2,1] 输出: [4,3,2,2] 解释: 输入数组表示数字 4321。解题思路
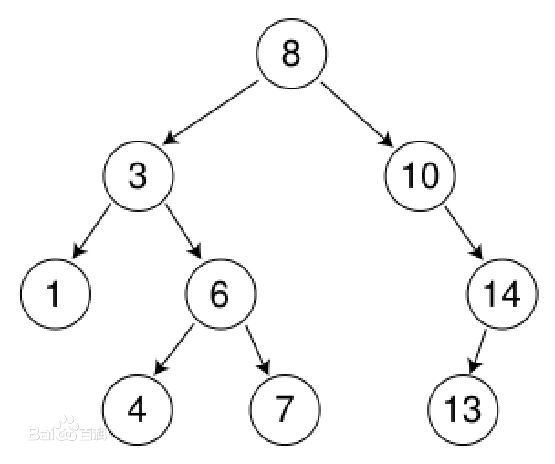
只需要判断有没有进位并模拟出它的进位方式,如十位数加 11 个位数置为 00,如此循环直到判断没有再进位就退出循环返回结果。
然后还有一些特殊情况就是当出现 9999、999999 之类的数字时,循环到最后也需要进位,出现这种情况时需要手动将它进一位。
视频
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一
public int[] plusOne(int[] digits) { for (int i = digits.length - 1; i >= 0; i--) { digits[i]++; digits[i] = digits[i] % 10; if (digits[i] != 0) return digits; } digits = new int[digits.length + 1]; digits[0] = 1; return digits; }删除元素
给定一个数组和一个值,在原地删除与值相同的数字,返回新数组的长度。
解题思路
- 定义一个 index 用于记录新数组下标,遍历数组
- 如果与传入值不同,则其应存在于新数组中 index++ 并存入
- 如果与传入值相同,说明重复,则直接跳过该数
- 最后返回 index 即可
public int removeElement(int[] A, int elem) { if (A == null || A.length == 0) { return 0; } int index = 0; for (int i = 0; i < A.length; i++) { if (A[i] != elem) { A[index++] = A[i]; } } return index; }删除排序数组中的重复数字
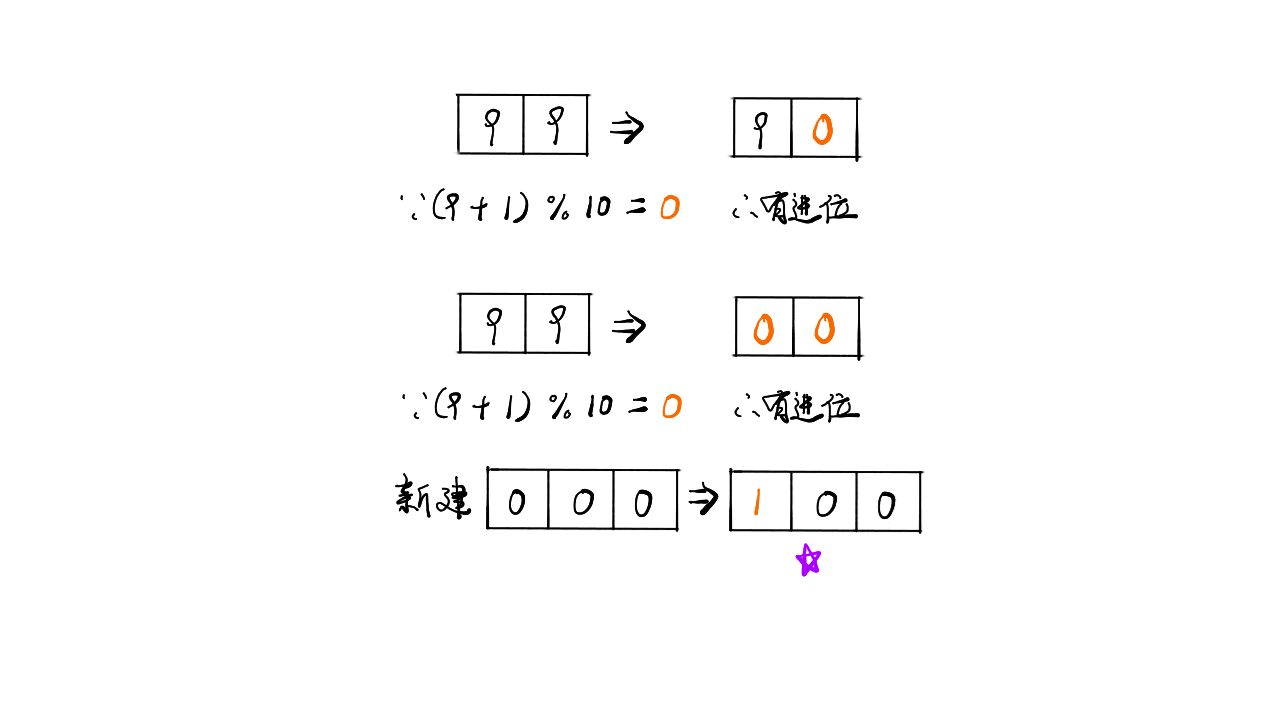
在原数组中“删除”重复出现的数字,使得每个元素只出现一次,并且返回“新”数组的长度。
示例 :
给定 nums = [0,0,1,1,1,2,2,3,3,4], 函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。 你不需要考虑数组中超出新长度后面的元素。解题步骤
- 数组完成排序后,我们可以放置两个指针 size 和 i,其中 size 是慢指针,而 i 是快指针。
- 只要 nums[size] = nums[i] ,我们就增加 i 以跳过重复项。
- 当我们遇到 nums[i] =nums[size] 时,跳过重复项的运行已经结束
- 因此我们必须把它(nums[i])的值复制到 nums[size+1]。
- 然后递增 i 接着我们将再次重复相同的过程,直到 size 到达数组的末尾为止。
public int removeDuplicates(int[] A) { if (A == null || A.length == 0) { return 0; } int size = 0; for (int i = 0; i < A.length; i++) { if (A[i] != A[size]) { A[++size] = A[i]; } } // (1) return size + 1; }注:因为 size 为下标,所以返回长度要加一
我的日程安排表 I
实现MyCalendar类来存储活动。如果新添加的活动没有重复,则可以添加。类将有方法book(int start,int end)。这代表左闭右开的间隔[start,end)有了预定,范围内的实数x,都满足start <= x < end,返回true。 否则,返回false,并且事件不会添加到日历中。
示例 :
MyCalendar(); MyCalendar.book(10, 20); // returns true MyCalendar.book(15, 25); // returns false MyCalendar.book(20, 30); // returns true 解释: 第一个日程安排可以添加到日历中. 第二个日程安排不能添加到日历中,因为时间 15 已经被第一个日程安排预定了。 第三个日程安排可以添加到日历中,因为第一个日程安排并不包含时间 20 。解题步骤
- TreeMap 是一个有序的key-value集合,它通过 红黑树 实现,继承于AbstractMap,所以它是一个Map,即一个key-value集合。
- TreeMap可以查询小于等于某个值的最大的key,也可查询大于等于某个值的最小的key。
- 元素的顺序可以改变,并且对新的数组不会有影响。
-
floorKey(K key) 方法用于返回小于或等于给定的键的所有键中,的最大键,或null,如果不存在这样的键
-
ceilingKey(K key) 方法用于返回大于或等于返回到给定的键中,的最小键,或null,如果不存在这样的键
class MyCalendar { TreeMap<Integer, Integer> calendar; MyCalendar() { calendar = new TreeMap(); } public boolean book(int start, int end) { Integer previous = calendar.floorKey(start), next = calendar.ceilingKey(start); if ((previous == null || calendar.get(previous) <= start) && (next == null || end <= next)) { calendar.put(start, end); return true; } return false; } }合并两个有序数组
合并两个排序的整数数组A和B变成一个新的数组。可以假设A具有足够的空间去添加B中的元素。
说明:
初始化 A 和 B 的元素数量分别为 m 和 n。
你可以假设 A 有足够的空间(空间大小大于或等于 m + n)来保存 B 中的元素。
示例:
输入: nums1 = [1,2,3,0,0,0], m = 3 nums2 = [2,5,6], n = 3 输出: [1,2,2,3,5,6]解题思路
- 双指针 / 从后往前
- 这里的指针 p 用于追踪添加元素的位置。
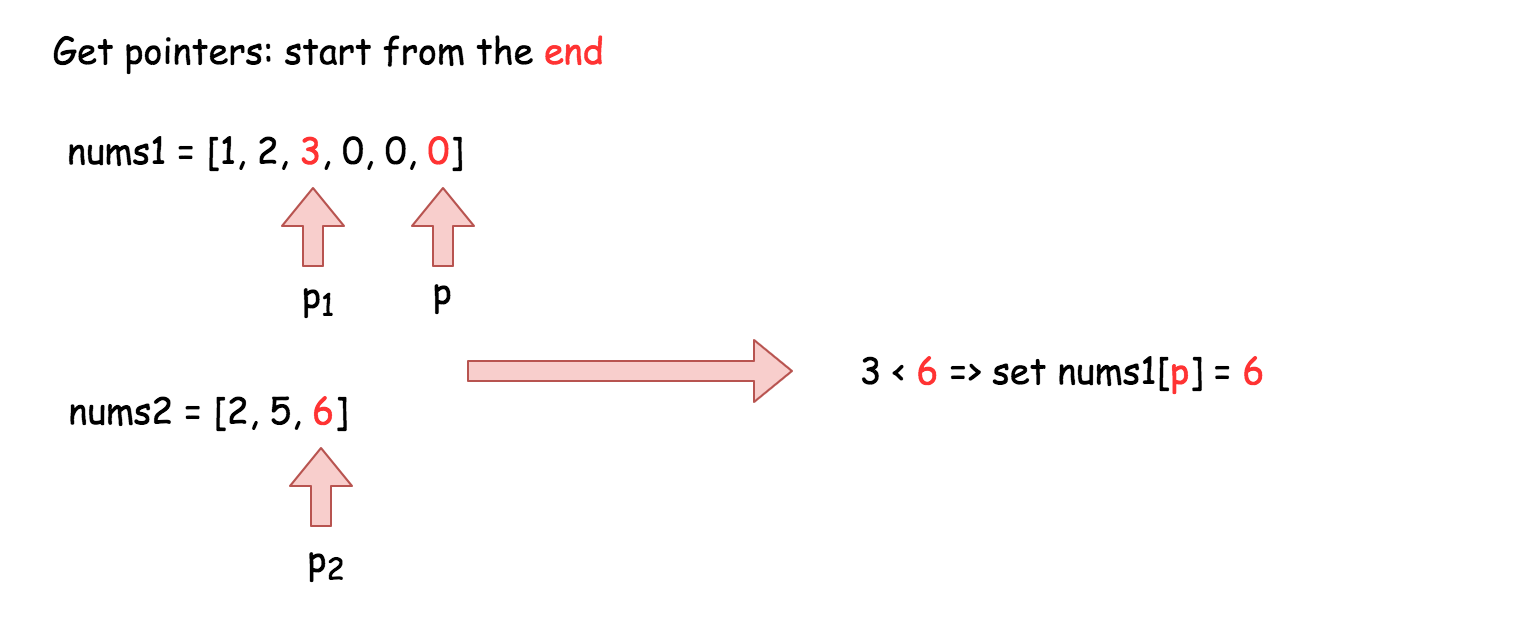

public void mergeSortedArray(int[] A, int m, int[] B, int n) { int i = m - 1, j = n - 1, index = m + n - 1; while (i >= 0 && j >= 0) { if (A[i] > B[j]) { A[index--] = A[i--]; } else { A[index--] = B[j--]; } } while (i >= 0) { A[index--] = A[i--]; } while (j >= 0) { A[index--] = B[j--]; } }贪心
顾名思义,贪心算法总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑,它所作出的选择只是在某种意义上的局部最优选择。当然,希望贪心算法得到的最终结果也是整体最优的。虽然贪心算法不能对所有问题都得到整体最优解,但对许多问题它能产生整体最优解。如单源最短路经问题,最小生成树问题等。在一些情况下,即使贪心算法不能得到整体最优解,其最终结果却是最优解的很好近似。
视频
买卖股票的最佳时机
假设有一个数组,它的第i个元素是一支给定的股票在第i天的价格。如果你最多只允许完成一次交易(例如,一次买卖股票),设计一个算法来找出最大利润。
注意:
- 你不能在买入股票前卖出股票。
示例 :
输入: [7,1,5,3,6,4] 输出: 5 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。如果将测试范例 [7, 1, 5, 3, 6, 4]
绘制成图,我们发现:
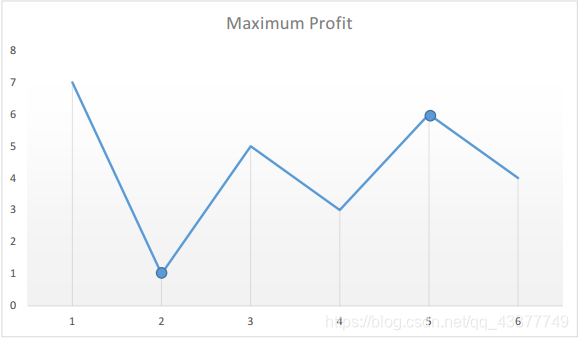
- 我们需要找到最小的谷之后的最大的峰。
- 我们可以维持两个变量 —— min 和 profit,它们分别对应迄今为止所得到的最小的谷值和最大的利润(卖出价格与最低价格之间的最大差值)。
public int maxProfit(int[] prices) { if (prices == null || prices.length == 0) { return 0; } int min = Integer.MAX_VALUE; //记录最低的价格 int profit = 0; for (int price : prices) { min = Math.min(price, min); profit = Math.max(price - min, profit); } return profit; }买卖股票的最佳时机 II
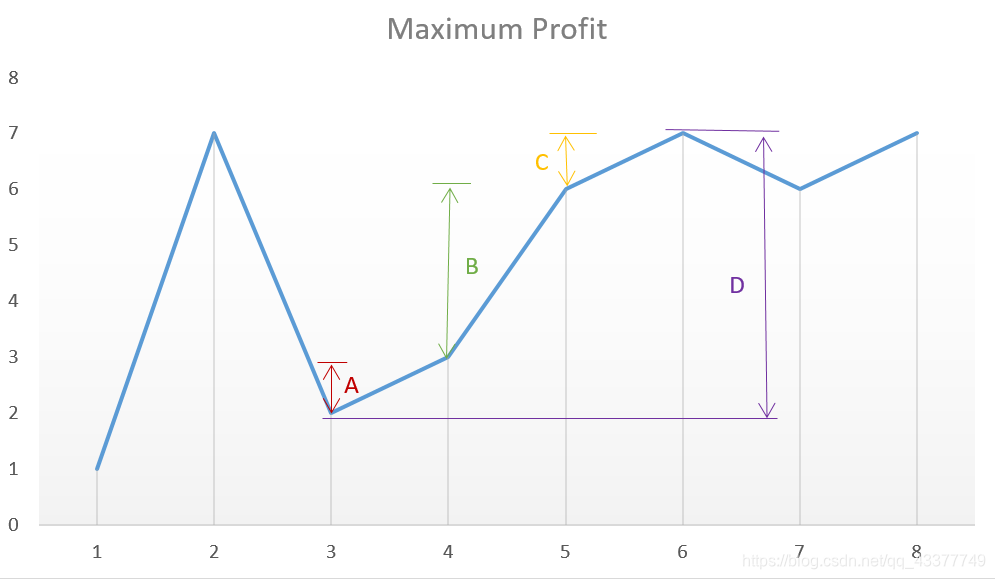
给定一个数组 prices 表示一支股票每天的价格。可以完成任意次数的交易, 不过不能同时参与多个交易,设计一个算法求出最大的利润。
解题思路
贪心:
- 只要相邻的两天股票的价格是上升的,
- 我们就进行一次交易, 获得一定利润。
视频
public int maxProfit(int[] prices) { int profit = 0; for(int i = 0 ; i < prices.length -1; i++) { if(prices[i + 1] > prices[i]) { profit += prices[i + 1] - prices[i]; } } return profit; }最大子数组
给定一个整数数组,找到一个具有最大和的子数组,返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。解题思路
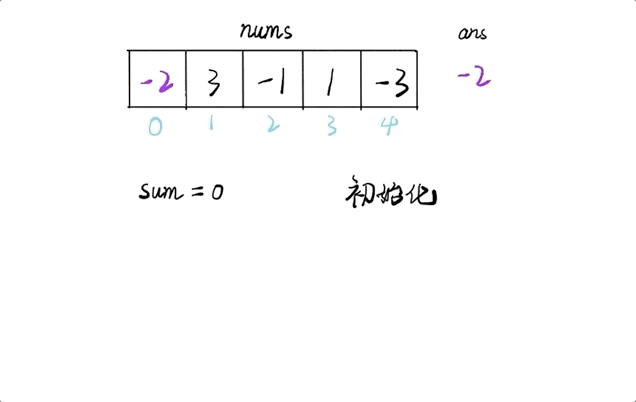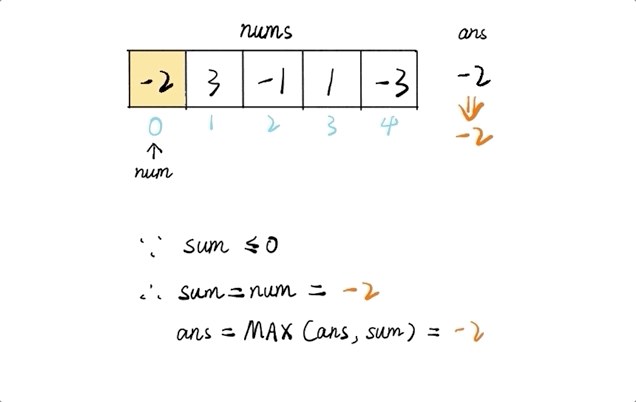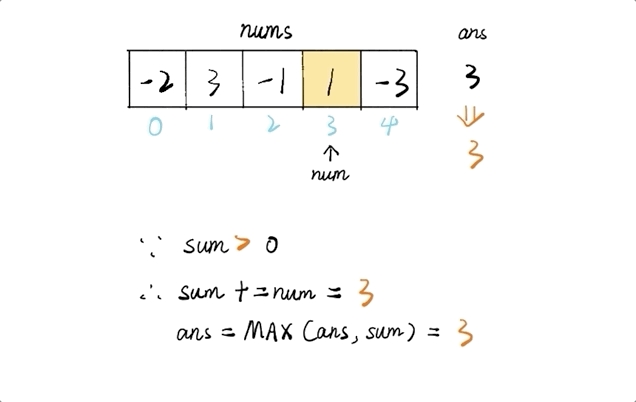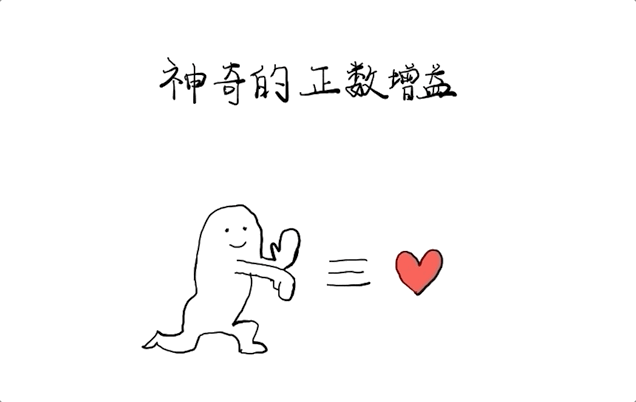
public int maxSubArray(int[] nums) { if(nums == null || nums.length == 0) { return 0; } int max = Integer.MIN_VALUE; int sum = 0; for (int num : nums) { sum += num; max = Math.max(sum, max); sum = Math.max(sum, 0); } return max; }主元素
给定一个整型数组,找出主元素,它在数组中的出现次数严格大于数组元素个数的二分之一(可以假设数组非空,且数组中总是存在主元素)。
解题思路
- 重点在于:主元素数量大于数组所有元素的二分之一
- 所以我们要做的是,选出一个出现次数大于其他所有数,出现次数和的数即可
- 设一个计数器 currentMajor 候选数 和 一个 count 用于记录次数
- 每当当前数和 currentMajor 值相同时, count 值 +1
- 每当当前数和 currentMajor 值不同时, count 值 -1
- 每次 count 等于 0 时,说明在之前访问的数组里 currentMajor 的数量小于或等于一半
- 则将 currentMajor 赋值为当前数,继续寻找。
public int majorityNumber(List<Integer> nums) { int currentMajor = 0; int count = 0; for(Integer num : nums) { if(count == 0) { currentMajor = num; } if(num == currentMajor) { count++; } else { count--; } } return currentMajor; }Attention
- 为了提高文章质量,防止冗长乏味
下一部分算法题
-
本片文章篇幅总结越长。我一直觉得,一片过长的文章,就像一堂超长的 会议/课堂,体验很不好,所以我打算再开一篇文章
-
在后续文章中,我将继续针对
链表栈队列堆动态规划矩阵位运算等近百种,面试高频算法题,及其图文解析 + 教学视频 + 范例代码,进行深入剖析有兴趣可以继续关注 _yuanhao 的编程世界 -
不求快,只求优质,每篇文章将以 2 ~ 3 天的周期进行更新,力求保持高质量输出
# 相关文章
面试高频算法题汇总「图文解析 + 教学视频 + 范例代码」之 二分 + 哈希表 + 堆 + 优先队列 合集
?面试必备:高频算法题汇总「图文解析 + 教学视频 + 范例代码」必知必会 排序 + 二叉树 部分!?
每个人都要学的图片压缩终极奥义,有效解决 Android 程序 OOM
Android 让你的 Room 搭上 RxJava 的顺风车 从重复的代码中解脱出来
ViewModel 和 ViewModelProvider.Factory:ViewModel 的创建者
单例模式-全局可用的 context 对象,这一篇就够了
缩放手势 ScaleGestureDetector 源码解析,这一篇就够了
Android 属性动画框架 ObjectAnimator、ValueAnimator ,这一篇就够了
看完这篇再不会 View 的动画框架,我跪搓衣板
看完这篇还不会 GestureDetector 手势检测,我跪搓衣板!
请点赞!因为你的鼓励是我写作的最大动力!

为了方便大家跟进学习,我在 GitHub 建立了一个仓库
仓库地址:超级干货!精心归纳视频、归类、总结,各位路过的老铁支持一下!给个 Star !

