[分治算法]因式分解

2019 年 10 月 13 日
筆記

整数因子分解问题

http://acm.sdut.edu.cn/onlinejudge2.dev/index.php/Home/Index/problemdetail/pid/1722.html

Time Limit: 1000 ms Memory Limit: 65536 KiB

Problem Description

大于1的正整数n可以分解为：n=x1*x2*…*xm。例如，当n=12 时，共有8 种不同的分解式：
12=12；
12=6*2；
12=4*3；
12=3*4；
12=3*2*2；
12=2*6；
12=2*3*2；
12=2*2*3。
对于给定的正整数n，计算n共有多少种不同的分解式。

Input

输入数据只有一行，有1个正整数n (1≤n≤2000000000)。

Output

将计算出的不同的分解式数输出。

Sample Input

Sample Output

算法一（超时）

算法思路：

　　比如以 12为例，情况1）与情况2）都应该计算在Count中，但情况2)是根据情况1)产生的。因此需要递归，每层函数对i进行遍历一遍，如果temp/i==0，说明该层的数可以被分解，再递归进入下一层。

代码：

 1 #include <iostream>   2 #include <algorithm>   3 using namespace std;   4   5 int Count;   6   7 // 来计算整数因子分解问题   8 void func(int temp) {   9  10     for (int i = 2; i < temp; i++) {  11         if (temp%i == 0) {  12             Count++;  13             func(temp / i);  14         }  15     }  16 }  17  18 int main() {  19  20     Count = 0;  21     int temp;  22     cin >> temp;  23     func(temp);  24     cout << Count+1 << endl;  25 }

算法二（优化）

算法一存在的弊端：我们求(i,temp/i）中 temp/i 的因式分解个数时，会重复计算(如下图）

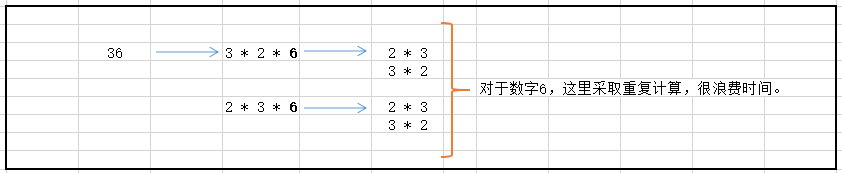
解决算法一的策略：我们采用一个数组直接存储数字6的因子，如果发现该arr[6]中存在数，则直接用避免重复计算。

算法思路：

依然采用递归，t = i * j，则 count(t) = count(i) + count(j)；为避免重复计算 (t = i * j = j * i)，应该限制 i < j，即 for(i;i<sqrt(t);i++)。